改进的粒子群算法在水库优化调度中应用
张忠波,何晓燕,耿思敏,李 辉,张大伟 ,姜晓明
(1.中国水利水电科学研究院,北京 100038; 2.水利部 防洪抗旱减灾工程技术研究中心,北京 100038)
1 研究背景
水库优化调度可实现水资源的合理分配和电能的可持续利用,对高效利用水资源具有非常重要的意义[1-2]。水库优化调度是典型的多维非线性优化问题,针对求解问题的复杂性、非线性等特点,求解方法显得尤其重要。动态规划等传统算法在实际应用中常常会遇到“维数灾”,由于动态规划法求解时,随着计算精度的提高,计算所需时间成指数倍增长,计算效率明显降低[3]。人们又提出了不少改进的传统优化算法,但在某些方面仍有其缺陷,如逐次逼近动态规划难以保证收敛到全局最优解等。随着水库电站数目的增多,“维数灾”成为水电站优化调度的瓶颈[4-5],针对粒子群算法(Parti⁃cle Swarm Optimization,缩写为 PSO)的特性,许多学者提出了改进的PSO算法(Improved PSO,简称IPSO),如Berhart and Shi(1998)就提出了惯性权值线性递减的PSO算法,对PSO算法性能有了明显改进。但这种线性递减惯性权值只与算法迭代次数有关,不能真实反映算法在运行过程中的复杂的、非线性变化的特性;另一方面,在运行后期,随着惯性权值的减小,PSO算法缺乏全局搜索能力。
许多学者提出了智能算法并应用到水库优化调度中[6-9],但求解精度和收敛速度仍不及预期。粒子群算法(PSO)应用到水库优化调度研究较多,张双虎等[10]采用改进惯性权值的方法改善了粒子群算法收敛性,其他学者也从惯性权值和收敛特性进行了一系列的改进[11-13]。PSO虽然简单易行,但粒子更新建立在速度更新和粒子之间信息的基础上,在一定程度上限制了全局寻优能力[14]。对于复杂的、强约束的系统优化问题,应用PSO算法求解粒子群寻优过程中表现出强烈的“趋同性”,使种群多样性损失过快,容易导致算法出现早熟收敛[15-16]。而下山搜索策略通过反射、扩展、收缩等方法大大增强种群的多样性,而单纯形与粒子群一一对应,该策略与PSO具有一定结合基础。本文结合下山搜索策略,提出改进的粒子群算法,并应用到三峡水库优化调度中求解中,探讨改进方法求解梯级水库优化调度模型的可行性和高效性,为水库调度提供一定参考依据。
2 水库优化调度模型
2.1目标函数水库优化调度一般是多目标决策问题,主要目标有防洪、发电、航运以及下游用水效益等。兴利效益一般以发电效益为评价指标时,而其它目标作为约束条件建立调度模型:

式中:F为电站年发电量,kW·h;K为电站综合出力系数,无量纲;Qt为t时段的发电流量,m3/s;Ht为电站在t时段平均发电净水头,m;T为年内计算总时段数;Nt为t时段的出力,kW;Tt为t时段时间,s。
由于水库优化调度是多目标决策,以兴利效益为单目标,通常采用约束法把其它目标作为约束条件把多目标决策转化为单目标决策。而在寻优过程会产生大量的不可行解,主要采用定量惩罚函数法来抑制不可行解的产生,如下式:
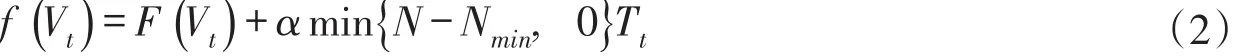
式中:f(Vt)为时段t适应度;F(Vt)为时段t发电量;α为惩罚系数[17],无量纲。
2.2约束条件
(1)水量平衡方程:Vt+1=Vt+( )
It-OtΔt,式中,Vt是t时段的水库库容,m3;It是t时段的入库流量,m3/s;Ot是t时段的出库流量,m3/s;Δt是时段长度,s。
(2)水位约束:Zl≤ Zt≤ Zu,Zl、Zt、Zu对应最低水位、时段t水位和最高水位,m。
(3)库容约束:Vlt≤ Vt≤ Vut,t=1,2,…,T,Vlt、Vut是t时段的最小库容和最大库容,m3。
(4)水库出库流量约束Ol≤ Ot≤ Ou, Ol、Ou是水库t时段的最小出库流量和最大泄流流量,m3/s。
(5)出力约束Nl≤ Nt≤ Nu,Nl、Nt、Nu对应最小出力、t时段出力和装机容量,kW。
3 改进的粒子群算法分析
3.1改进的粒子群算法PSO算法由Kenndy和 Eberhart在1995年提出[18],其基本思想:通过群体中个体之间的协作和信息共享来寻找最优解。单纯形算法由Splendy等1962年提出,Nelder和Mead(1965)针对该算法不能加速搜索[19],以及在曲谷中或曲脊上进行搜索所遇到的困难做了改善,提出了下山搜索策略,指n空间En中具有n+1个顶点的凸多面体,求出单纯形n+1个顶点上的函数值,确定出函数最大值点(最高点)和函数最小值点(最低值点),然后通过反射、扩展、收缩等方法(几种方法不一定同时用)求出一个较好点,取代最高点,构成新的单纯形,或者通过向最低点收缩形成新的单纯形,用这样的方法来逼近最小点[19](如图1)。为了提高粒子群算法全局搜索能力和收敛性能,把下山搜索策略引入到粒子群智能算法中,提出了改进的粒子群算法(simplex downhill search PSO,简称SDSPSO)。
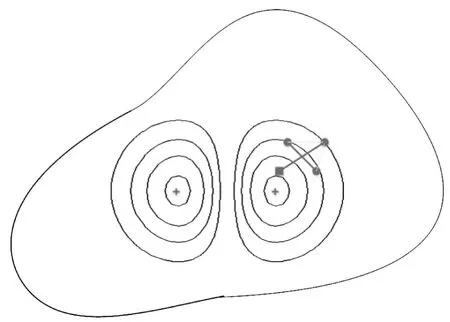
图1 单纯形“下山”搜索策略示意图
SDSPSO算法具体步骤如下:
根据上述基本PSO(Origin PSO,OPSO)的基本原理,SDSPSO求解优化问题的步骤如下(图2)。
(1)步骤1:初始化粒子种群。设k=0,根据具体研究问题为N维,选取参与进化的复合形个数Q和每个复合形所包含的顶点数M,随机生成L=QM个粒子,其中,分别为第q复合形的m个粒子的位置向量和速度向量,
(3)步骤3:更新局部最佳个体和全局最佳个体。找到目前每个复合形的最佳适应度值记为同时记下当前位置向量为;找到目前群体的最佳适应度值记为记位置向量为,
(4)步骤4:更新每个复合形中的个体位置向量和速度向量,产生下一代粒子群。
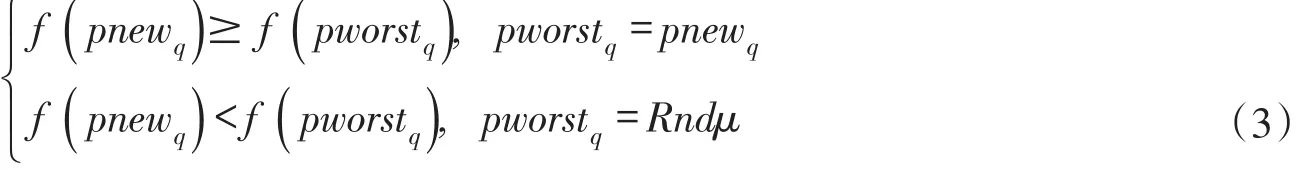
对复合形中其它个体的每一个速度元素和位置元素,采用下式进行更新:

(5)步骤5:检验是否满足算法迭代终止条件,若满足,则停止迭代,输出最优结果;否则令k=k+1,转向Step2。迭代终止条件k=K(K为预先设置的最大迭代次数);或

图2 SDSPSO算法求解步骤

表1 测试函数

3.2算法验证为测试改进粒子群算法的性能,选用表1中测试函数对算法进行测试。为验证改进算法适应高维优化计算问题,选取高维的测试函数(30维)进行测试,并给出了测试函数变量的取值范围,以及理论最优值。
为验证改进算法的有效性,分别选择跟基本粒子群算法(OPSO),以及Berhart and Shi(1998)[20]
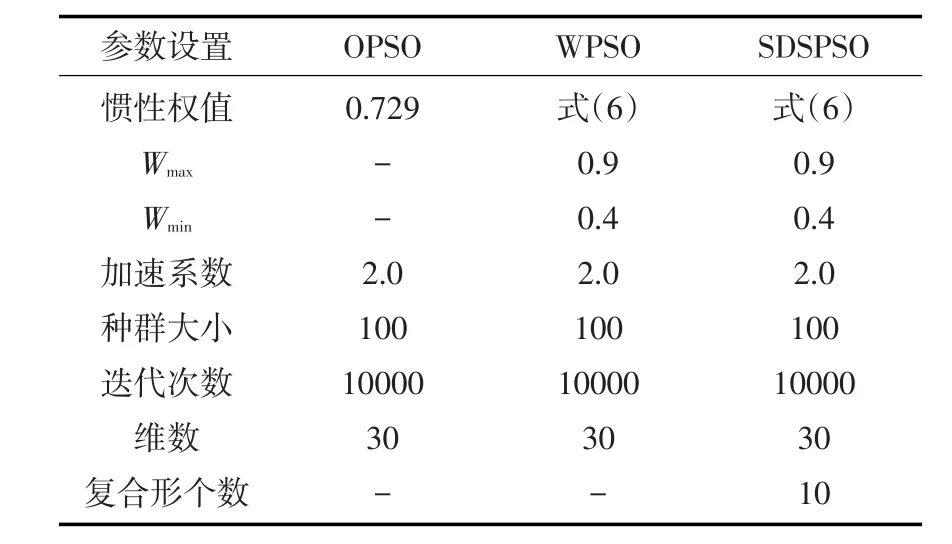
表2 各个算法参数设置

表3 不同算法计算得到的测试函数最优值
就提出了惯性权值线性递减的PSO算法(简称WPSO)进行比较,其惯性权值计算公式如下:

各个算法参数设置如表2所示。
根据表2设置的参数,采用FORTRAN编码,各个算法计算的最优值如表3所示。
从表3可以看出,相比较于其它两个算法而言,提出改进PSO求解函数3和函数4时最优结果为0和-1.4E-45,可认为已经求出了函数真实的最优值,WPSO同样也求出了函数3的最优值,其他函数最优值远远低于SDSPSO;而OPSO整体上所求结果最差。通过多次实验分析,SDSPSO改善了测试函数收敛精度,改进的算法收敛精度,从而得到较好的求解结果。各个算法求解收敛速度及进化过程见图3。
4 实例应用
三峡工程是开发长江水资源的重要工程,水库正常蓄水位175 m,防洪限制水位145 m,枯期消落低水位155m,具有巨大的防洪、发电和航运等综合效益。三峡水库防洪库容221.5亿m3,兴利库容165.0亿m3,有巨大的调蓄能力,具体参数值见表4。由于三峡水库可进行年调节,而汛期基本保持汛限水位不变,所以对供水期进行优化调度更加合理,即从开始蓄水到翌年的汛前进行优化调度,采用旬为计算时段。以典型枯水年、平水年和丰水年的供水期作为研究对象,选取三峡坝址宜昌水文站的径流系列作为研究依据。以水库供水期作为水库优化调度分析对象,根据长江水利委员会制定的调度方案[21-22],规定9月1日到翌年6月10日为三峡水库供水期,单个粒子共有28个个体。
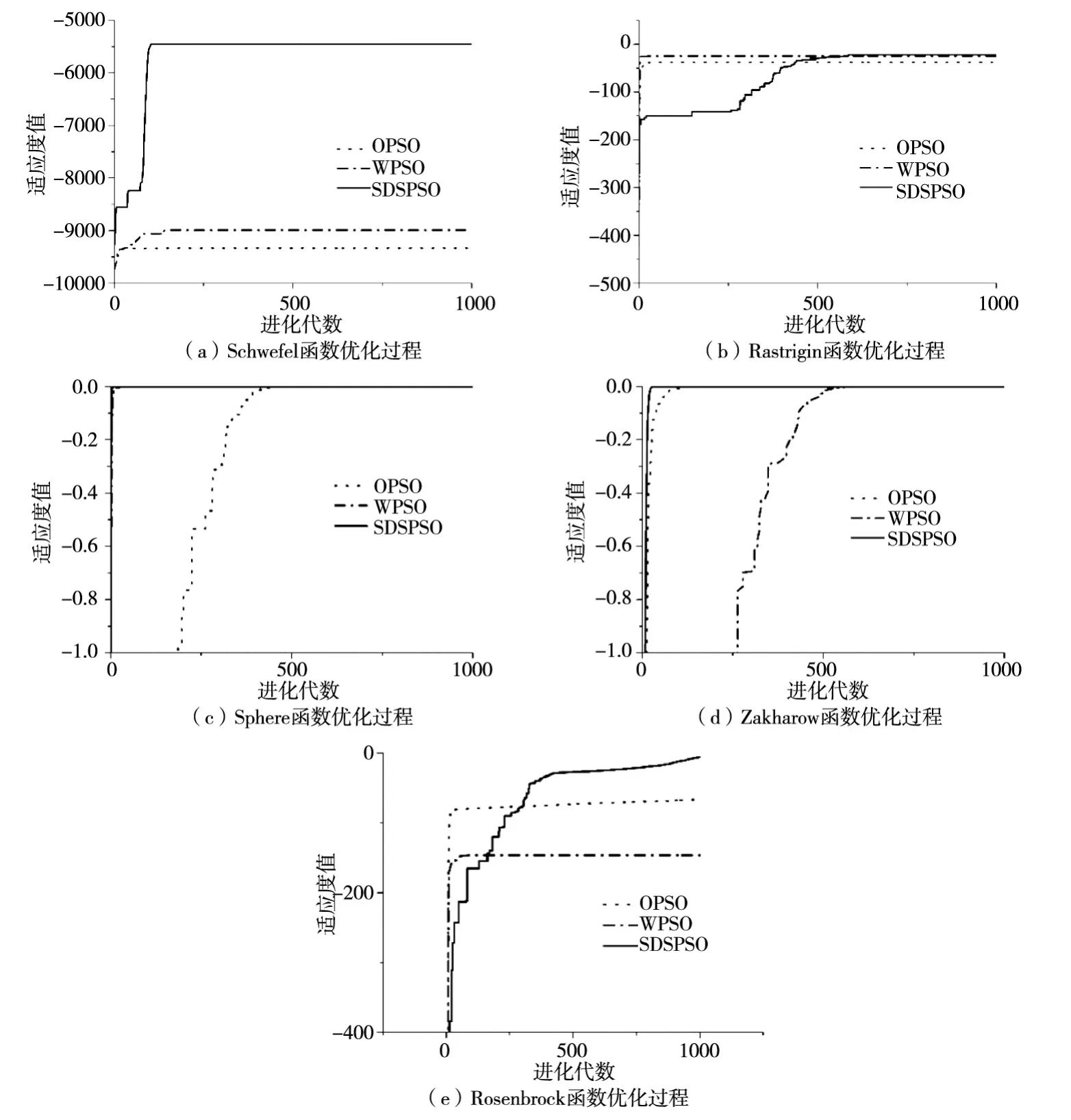
图3 各个算法进化过程比较

表4 三峡电站的具体参数值

表5 典型年对应年份
为了验证算法的有效性,分别选取典型年(表5)丰水年、平水年和枯水年的9月1日到翌年6月10日为优化时段,采用三种算法分别建立优化调度
模型求解,种群分别选取了100、200和300,计算结果如表6所示。

表6 各个算法计算不同典型年及不同种群对应优化结果 (单位:亿kW·

图4 部分典型年水库调度优化过程
从表6可以看出,相比于其他两种算法,提出SDSPSO能够得到较好的优化结果,而且随着种群增加,求解精度不断提高,其中丰水年供水期平均可增发电量11.18亿和18.97亿kW·h;平水年供水期平均可增发电量21.11亿和20.75亿kW·h;枯水年供水期平均可增发电量12.71亿和1.23亿kW·h;长系列供水期平均可增发电量15亿和13.65亿kW·h。图4(a)(b)(c)给出部分典型年不同种群的优化调度结果,SDSPSO取得了较好的求解结果。
5 结论
基于下山搜索策略,提出了改进的粒子群算法,并将改进算法应用到三峡水库实际调度中。通过对5个测试函数优化可知,相比较于其它两个算法而言,提出改进PSO求解函数3和函数4时最优结果为0和-1.4E-45,可认为已经求出了函数真实的最优值,WPSO同样也求出了函数3的最优值,其他函数最优值远远低于SDSPSO;而OPSO整体上所求结果最差。通过多次实验分析,SDSPSO改善了测试函数收敛精度,改进的算法收敛精度,从而得到较好的求解结果。并把改进的PSO算法应用到三峡工程实例中,分别选取了丰水年、平水年和枯水年作为优化模型输入条件,采用三种算法进行优化计算。与其他两个算法相比较,改进粒子群算法提高了收敛速度并改善了调度效益,其中丰水年供水期平均可增发电量11.18亿和18.97亿kW·h;平水年供水期平均可增发电量21.11亿和20.75亿kW·h;枯水年供水期平均可增发电量12.71亿和1.23亿kW·h。而长系列计算结果进一步验证了改进算法的有效性,长系列供水期平均可增发电量15亿和13.65亿kW·h。计算结果表明:该方法易于实现,求解效率高,为水库优化调度问题求解提供了一定参考。
[1] 刘涵.水库优化调度新方法研究[D].西安:西安理工大学,2006.
[2] ZHANG Zhongbo,JIANG Yunzhong,ZHANG Shuanghu,et al.An improved adaptive particle swarm optimiza⁃tion algorithm for reservoir operation optimization[J].Appl Soft Comput,2014(18):167-177.
[3] 程春田,郜哓亚,武新宇,等.梯级水电站长期优化调度的细粒度并行离散微分动态规划方法[J].中国电机工程学报,2011,31(10):26-32.
[4] 李安强,张建云,仲志余,等.长江流域上游控制性水库群联合防洪调度研究[J].水利学报,2013,44(1):59-66.
[5] 谢维,纪昌明,吴月秋,等.基于文化粒子群算法的水库防洪优化调度[J].水利学报,2010,41(4):452-457,463.
[6] 雷德明,严新平.多目标智能优化算法及其应用[M].北京:科学出版社,2009.
[7] 陈立华,梅亚东,董雅洁,等.改进遗传算法及其在水库群优化调度中的应用[J].水利学报,2008,39(5):550-556.
[8] JANGA Reddy M,NAGESH Kumar D.Optimal reservoir operation usingmulti-objective evolutionary algorithm[J].Water Resource.Management,2006,20(6):861-878.
[9] NAGESH Kumar D,JANGA Reddy M.Multipurpose reservoir operation using particle swarm optimization[J].Journal of Water Resources Planning and Management,2007,133(3):192-201.
[10] 张双虎,黄强,吴洪寿,等.水电站水库优化调度的改进粒子群算法[J].水力发电学报,2007,26(1):1-5.
[11] 杨道辉,马光文,过夏明,等.粒子群算法在水电站优化调度中的应用[J].水力发电学报,2006,25(5):5-7.
[12] JONG-YulKim,KYEONG-Jun Munb,HYUNG-Su Kim,et al.Optimal power system operation using parallel processing system and PSO algorithm[J].Int.J.Elec.Power.,2011,33:1457-1461.
[13] CHEN R M.Particle swarm optimization with justification and designed mechanisms for resource-constrained project scheduling problem[J].ExpSyst Appl.,2011,38:7102-7111.
[14] AFSHAR M H.Large scale reservoir operation by constrained particle swarm optimization algorithms[J].J.Hy⁃dro-environ Res.,2012(6):75-87.
[15] 刘本希,廖胜利,程春田,等.库群长期优化调度的多核并行禁忌遗传算法[J].水利学报,2012,43(11):1279-1286.
[16] 邹强,王学敏,李安强,等.基于并行混沌量子粒子群算法的梯级水库群防洪优化调度研究[J].水利学报,2016,47(8):967-976.
[17] GAO Hao,SAM Kwong,YANG Jijiang.Particle swarm optimization based on intermediate disturbance strategy algorithm and its application in multi-threshold image segmentation[J] .Information Sciences,2013,250(2013),82-112.
[18] EBERHART R,KENNEDY J.A New Optimizer Using Particle Swarm Theory[C]//MHS’95 Proceedings of the Sixth International Symposium on Micro Machineand Human Science,1995.
[19] NELDER J A,MEAD R.A Simplex method for function minimization[J].Comput.J.,1965(7):308-313.
[20] SHI Y,EBERHART R C.A Modified Particle Swarm Optimizer[C]//Proc.IEEE Congr.Evol.Comput.,1998.
[21] 中华人民共和国水利部.三峡水库优化调度方案[R].北京:中华人民共和国水利部,2009.
[22] 长江水利委员会.三峡工程综合利用与水库调度研究[M].武汉:湖北科学技术出版社,1997.

