基于时频单源点检测的雷达信号的盲分选

翁国秀，徐学红

(1.玉林师范学院 教育技术中心,广西 玉林 537000; 2.河南牧业经济学院 信息与电子工程学院，郑州 450044)

基于时频单源点检测的雷达信号的盲分选

翁国秀1，徐学红2

(1.玉林师范学院 教育技术中心,广西 玉林 537000; 2.河南牧业经济学院 信息与电子工程学院，郑州 450044)

针对欠定条件下的雷达信号分选问题，提出一种基于时频单源点检测的雷达信号盲分选算法,该分选算法的创新点在于将雷达信号由时域转移到时频域进行分析。在时频域内，雷达信号具有一定的稀疏性，有助于实现信号盲分选，给出了基于时频单源点检测的雷达信号盲分选算法的具体步骤。该方法能够有效解决欠定条件下雷达信号盲分选问题，将其应用于雷达信号分选领域，具有一定的军事应用价值。仿真测试结果表明了该方法的可行性与优越性。

时频变换;单源点;雷达信号;聚类验证;盲分选

0 引 言

雷达信号的盲分选技术是盲信号分离技术在雷达信号处理领域里的应用，近年来国内外有相关的研究。文献[1]中利用空间四阶累计矩阵对雷达信号进行盲分离，实现信号分选过程，仿真实验也表明盲分离方法能够应用于信号分选当中，并且有很好的分离效果。但在文献的仿真部分，已知辐射源个数，对于未知辐射源个数的信号分选情况，文献并未提及。文献[2]中利用定点独立分量分析的方法，对超定情况下的雷达信号进行盲分离，通过仿真表明，分离出的雷达信号与源信号相比信号相似比高，且提高了信噪比，保留了杂波信息，但是欠定条件下的信号分选文章并未提及。文献[3]中提出了基于k均值聚类的盲辨识算法，解决了欠定的信号盲分解问题。文献[4]中将等间隔分段的观测信号应用于独立分量分析，在雷达信号不充分稀疏的情况下解决了信号分离问题，但是文献[3]和文献[4]对信号的分解在很大程度上还得依靠信号的稀疏分解统计量。

针对以上算法的不足，本文根据文献[5-6]的思想，提出一种基于时频单源点检测的方法，在不依赖信号稀疏性的欠定条件下，解决未知辐射源个数的雷达信号分选问题。通过建立雷达源信号时域波形，对信号时域波形的进一步分析，得到信号频谱图，从而完成信号分选过程。最后通过模拟实验验证该算法的正确性与有效性。

1 问题描述

设雷达信号数量为P，同时向同一空域内进行辐射；接收天线为M元均匀阵列，则在接收到的信号可以表示

(1)

(1)式中：x(t)=[x1(t),x2(t),…,xM(t)]T为观测信号；s(t)=[s1(t),s2(t),…,sP(t)]T为雷达发射信号；n(t)=[n1(t),n2(t),…,nM(t)]T为天线噪声信号；在观测模型中，雷达发射信号与噪声信号是相互独立的；A为混合矩阵，表示为A=[α1,α2，…,αP]T。矩阵A中，第(i,k)个元素可表示为

(2)

(2)式中：bik表示第k个雷达信号源到第i个接收机时的幅度衰减量；τik表示第k个雷达信号源到第i个接收机时的时间延迟，且k∈[1,P]，i∈[1,M]；fk为源信号的频率。利用短时傅里叶变换(short-time Fourier transform, STFT)将信号进行稀疏表示[9-13]。本文利用线性调频信号作为目标信号，则信号可表示为

(3)

(3)式中：ω0为信号载频；ω1为信号的调制率；θ0为信号初相。为简化公式推导，本文中初相为0。对(1)式两边进行短时傅里叶变换，得

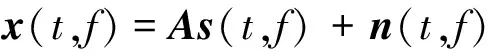
(4)

(4)式中：t,f张成的平面即为整个时频平面；x(t,f)，s(t,f)，n(t,f)分别是观测矩阵、信号矩阵以及噪声矩阵的短时傅里叶变换的结果。

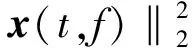
定义2 若在整个时频平面中，任意一点(t,f)上有si(t,f)≫sk(t,f)i≠k时，则认为在点(t,f)上只存在信号si(t,f)，所以，定义点(t,f)为信号si(t,f)的时频单源点。

为了完成对信号的盲分选，提出假设：设每一个信号都存在着离散的时频单源点。将不同的时频单源点检测出来，并完成混合矢量的估计，再将估计出的混合矢量组成矩阵即形成了混合矩阵[14]。准确估计的混合矩阵将观测信号进行解混，得到每一雷达源信号的时域波形，对时域波形的进一步分析。

2 算法推导

假设雷达信号sk(t)的时频单源点集合为Ψ(tki,fki)，其中，ki表示信号时频点的取值范围所在时频单源点集合中，任意一点的观测信号[15]可表示为

(5)

即在单源点集合中的任一点只存在一个源信号。为简化计算，忽略天线噪声存在，即

(6)

(6)式中，

(7)

(7)式中：ak为1×M维行向量，是整个混合矩阵中的第k行。计算出接收天线信号时频比得

(8)

(8)式中，m∈{1,2,…,M}，则当观测信号处于单源点时，根据(6)式可知，其信号的时频比为常数。即

(9)

所以，只需找到信号sk(t)的所有单源点，就可以对信号sk(t)对应的混合矢量进行估计，得

(10)

(10)式中，Lk为信号单源点的个数。利用混合信号的聚类特性，统计检测单源点。

考虑噪声信号后，时频比矩阵变成复矩阵，对于复数而言，分别对其实部及虚部进行直方统计。分别提取时频比矩阵中每一元素的实部、虚部，分别将实部、虚部的取值分为M1，M2组，各组对应的列矢量分别构成了M1，M2个子矩阵，剔除少于列K1，K2的矩阵，剩余的矩阵分别表示为Rjk与Ijk。令m=1时，对应的时频比矩阵可以表示为

(11)

则对于(10)式中的混合矢量的估计可表示为

(12)

(12)式中，“：”表示矩阵的所有行。将(3)式代入(6)式，得

(13)

(14)

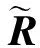
(15)

由前文可知，在单源点处只存在一个源信号，又根据奇异值分解特性，当只存在一个信号时，S中最大的奇异值对应的向量就是对混合矢量的估计。则奇异值矩阵S中最大值对应酉矩阵U=[u1,u2,…,uM]中的奇异值向量，即

(16)

(16)式中：uSmax表示S中最大值对应的奇异值向量。上述只是当m=1时的情况，改变m的取值，重复上述过程，即可求出所有混合矢量估计。

3 混合矩阵估计

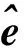
(17)

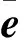
(18)

紧密程度表达式定义了混合估计矩阵间的可分离性，越不紧密的类分离效果越好。通过紧密程度表达式的调整，可以将紧密的类归为一类，将稀疏的类分离，这样不断优化，就可以找到紧密程度越弱的类。最终得到的混合矩阵中的类应该是紧密程度最弱的类的组合。

步骤3 为定量求出不同类别之间的可分离程度[17]，利用两类心之间的“距离”定义可分离程度，表达式为

(19)

(20)

(20)式中：“T”表示转置；“^”表示估计值。根据该方法估计出的混合矩阵，不再受传统聚类方法需要假设源信号个数的条件，利用各类心之间的“距离”函数来说明不同类别之间的分类程度。将类别数目作为变量，改变类别数目计算dis(c)的值，当函数值达到最小则说明分类程度最大，类别之间的相关性最小，即得到混合矩阵的估计。

4 模拟仿真及结果分析

4.1 实验数据设置

假设雷达源信号为4个线性调频(linear frequency modulation, LFM)信号，接收天线阵元数目为3个。至于检测门限ξ、统计参数M1，M2均与噪声因素相关，在不同的信噪比条件下，设定值均不相同，应在同一信噪比下进行多次试验，并且根据最终所需要的分类结果的标准设定不同的参数，使最终结果最优。

为了说明算法的有效性，选取的4个线性调频信号，fs=5 000 Hz，数据采样点数为N=10 000，信号的起始频率为[100，200，300，400]，调制率为[400，500，600，700]选取一个时宽内的采样点作为仿真信号。

混合矩阵A为

从对应混合矩阵估计可以看出，该分选方法得到的结果在信号顺序上出现了差异，但是，对于雷达信号分选问题而言，感兴趣的只是雷达信号的特征信息，所以，信号顺序的差异对于雷达侦察并无影响。

估计出混合矩阵后，对信号进行复原。根据(6)式可知，得到源信号矩阵，即

(21)

在欠定条件下，混合矩阵为M×P维，且M

(22)

(23)

(23)式中，“+”表示广义逆。

4.2 时频图与时域图

实验1：仿真出时频图与时域图。

由于Matlab仿真软件本身对于求逆矩阵问题存在固有误差，则在进行求解估计出的混合矩阵的逆矩阵问题时，误差较大。为解决这个问题，这里采用多次迭代的方法对误差进行降低甚至消除误差。则通过迭代法求广义逆矩阵后得到的复原信号的时频图如图1a所示。

图1 复原信号时频、时域波形对比图Fig.1 Comparison images of signal time frequency, time domain waveform

图1b，图1c分别为源信号时域波形和估计信号时域波形。由前文可知，雷达源信号的波形估计很大程度上依赖于混合矩阵的估计。所以，混合矩阵的估计精度直接影响着雷达信号分选的最终结果。即将雷达信号分选问题转化为对混合矩阵的估计问题，只要准确估计出混合矩阵，雷达源信号波形就能够准确得到。从估计矩阵的结果来看，证明了基于本文算法的雷达信号的盲分选方法有效。

4.3 信号分选效果

实验2：探究该方法在不同信噪比下的分选效果。

定义矩阵估计误差EA，即

(21)

图2 信噪比对估计性能的影响Fig.2 SNR effect on estimation performance

由图2可以看出，该方法信噪比逐渐提高的情况下，矩阵估计误差EA值越来越小，即估计精度越来越高。但整个信噪比范围中，EA值始终处于负值，说明该方法对于低信噪比条件下的雷达信号分选也有着较理想的分选效果。

4.4 算法收敛性

实验3：验证本方法与同类算法的优越性。

将本文方法与TIFROM(time-frequency ratio of mixtures)算法以及利用传统k均值的聚类的方法进行对比。在信噪比连续变化的条件下，对比各个方法之间的矩阵估计误差，从而衡量各方法之间的优劣。本实验中，信噪比由-20 dB以1 dB的步长增长至20 dB，每一信噪比条件下进行500次蒙特卡洛分析，最终得到对比结果如图3所示。

图3 TIFROM,k均值聚类及本文算法性能比较Fig.3 Performance comparison between TIFROM and k means clustering algorithm

由图3可以看出，基于k均值聚类方法针对于未知雷达源信号个数的情况的矩阵估计误差一直处于高值，估计混合矩阵效果基本随信噪比不变；而TIFROM算法与本文提出的算法在解决雷达信号混合矩阵估计的问题的时候，随着信噪比的提高，估计矩阵误差降低，同时，由图3还可看出，本文提出的算法矩阵估计误差收敛速度较快，即本文提出的算法适用性更强。

4.5 估计的成功率测试

实验4：基于k均值聚类检测技术对类心个数估计的成功率。

由基于k均值聚类检测技术提出的方法，利用假设的cmax值对于类心个数进行估计。该实验就是检测k均值聚类检测技术的成功率。假设cmax值为5，6，7，分别在不同cmax值的情况下，信源数目为4，即类心数目为4。在信噪比为-20～20 dB连续变化，步长为2 dB，在每一信噪比条件下进行100次蒙特卡洛分析，得到该检测技术在不同信噪比条件下的估计类心个数的准确率，如表1所示，最终结果如图4所示。

由图4可以看出，只要cmax的值足够大，大于类心数目就可以准确估计出类心数目，实现k均值的聚类。该实验证明了提出的优化的k均值聚类检测技术的有效性，该检测技术是对于类心的准确估计。所以只要设定的cmax值大于类心数目，即：cmax>P就能够完成估计。

表1 不同类心个数估计结果

图4 不同Cmax对类心个数估计的影响Fig.4 Effects on number of classes center with different Cmax

5 结 语

本文针对雷达信号分选算法进行了研究，提出了一种基于时频单源点检测的雷达信号盲分选的方法。仿真及结果表明，本文的雷达信号分选方法，能有效解决欠定条件下的雷达信号分选问题。该方法主要具备以下3个特点：①能够克服未知源信号个数的困难；②有效解决欠定条件下雷达信号分选问题；③该算法对于信噪比的适应范围较广。仿真结果表明，该方法能够分离出欠定条件下的雷达信号，具有很好的实用价值。

[1] 孙洪, 安黄彬. 一种基于盲源分离的雷达信号分选方法[J]. 现代雷达, 2006, 23(3): 47-50. SUN Hong, AN Huangbin. A Method to Select Radar Signal Based on Blind Source Separation[J]. Modern Radar, 2006, 23(3): 47-50.

[2] 肖文书, 张兴敢, 都思丹. 雷达信号的盲分离[J]. 南京大学学报, 2006, 42(1): 38-43. XIAO Wenshu, ZHANG Xinggan, DU Sidan. Blind Separation of Radar Signals[J]. Journal of Nanjing University, 2006, 42(1): 38-43.

[3] LI Y Q, CICHOCKI A, AMARI S I. Analysis of Sparse Representation and Blind Source Separation[J].Neural Computation, 2004(16): 1193 -1234.

[4] 陈晓军,成昊,唐斌.基于ICA的雷达信号欠定盲分离算法[J].电子与信息学报,2010,32(4):919-924. CHEN Xiaojun, CHENG Hao, TANG Bin. Underdetermined Blind Radar Signal Separation Based on ICA[J]. Journal of Electronics & Information Technology, 2010, 32(4): 919-924.

[5] ABRARD F，DEVILLE Y．A Time-Frequency Blind Signal Separationmethod Applicable to Underdetermined Mixtures of Dependent Sources[J]. Signal Processing, 2005(85):1389- 1403

[6] 杨杰,俞文文,田昊,等.基于独立分量分析的欠定盲源分离方法[J]. 振动与冲击, 2013, 32(7): 30-33. YANG Jie, YU Wenwen, TIAN Hao, et al. Underdetermined Blind Source Separation Method Based on Independent Component Analysis[J]. Journal of Vibration and Shock, 2013, 32(7): 30-33.

[7] PAKHIRA M K，BANDYOPADHYAY S，MAULIK U. Validity Index for Crisp and Fuzzy Clusters[J]. Pattern Recognition, 2004(37): 487-501.

[8] 阮宗利,李立萍,钱国兵,等.基于含噪复值ICA信号模型的快速不动点算法[J]. 电子与信息学报, 2014, 36(5): 1094-1099. RUAN Zongli, LI Liping, QIAN Guobing, et al. Fast Fixed-point Aalgorithm Based on Complex ICA Signal Model with Noise[J]. Journal of Electronics & Information Technology, 2014, 36(5): 1094-1099.

[9] 梁国龙,董姝敏.相干源盲分离及方位估计的算法研究[J].哈尔滨工程大学学报,2010,31(11):1478-1484. LIANG Guolong, DONG Shumin. Study on Algorithms of Blind Separation and DOA Estimation About Coherent Sources[J].Journal of Harbin Engineering University, 2010, 31(11): 1478-1484.

[10] BIN G, WOO W L, Dlay S S. Single-Channel Source Separation Using EMD-Subband Variable Regularized Sparse Features[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(4): 961-976.

[11] KLAUS N, ESA O, HANNUN O. On the Performance Indices of ICA and Blind Source Separation[C]∥2011 IEEE 12th International Workshop on Signal Processing Advances in Wireless Communications. Orleans, Orleans: IEEE, 2011: 461-465.

[12] ILMONEN P, NEVALAINEN J, OJA H. Characteristics of Multivariate Distributions and the Invariant Coordinate System[J]. Statistics and Probability Letters, 2010,80(23-24): 1844-1853.

[13] 顾凡, 王惠刚, 李虎雄. 一种强混响环境下的盲语音分离算法[J]. 信号处理, 2011,27(4):534-540. GU Fan, WANG Huigang, LI Huxiong. A Blind Speech Separation Algorithm with Strong Reverberation[J]. Signal Processing, 2011, 27(4): 534-540.

[14] 谭北海, 谢胜利. 基于源信号数目估计的欠定盲分离[J]. 电子与信息学报,2008,30(4):863-867. TAN Beihai, XIE Shengli. Underdetermined Blind Separation Based on Source Signals Number Estimation[J]. Journal of Electronics & Information Technology, 2008, 30(4): 863-867.

[15] 林波, 张增辉, 朱炬波. 基于压缩感知的 DOA 估计稀疏化模型与性能分析[J]. 电子与信息学报, 2014, 36(3): 589-894. LIN Bo, ZHANG Zenghui, ZHU Jubo. Sparsity Model and Performance Analysis of DOA Estimation with Compressive Sensing[J]. Journal of Electronics & Information Technology, 2014, 36(3): 589-894.

[16] 韩韬,周一宇.雷达信号的扩散特征及其在特定辐射源识别中的应用[J].电子学报,2013,41(3):502-507. HAN Tao, ZHOU Yiyu. Diffusion features in radar specific emitter identification[J]. Acta Electronica Sinica, 2013, 41(3): 502-507.

[17] 王磊, 史亚, 姬红兵. 基于多集典型相关分析的雷达辐射源指纹识别[J]. 西安电子科技大学学报:自然科学版, 2013, 40(2): 164-171. WANG Lei, SHI Ya, JI Hongbin. Specific radar emitter identification using multiset canonical correlation analysis[J]. Journal of Xidian University: Natural Science Edition, 2013, 40(2): 164-171.

[18] 宋爱民,李堰,刘剑,等.非圆信号多级维纳滤波DOA估计求根算法[J]. 电子科技大学学报, 2013, 42(1): 53-57. SONG Aimin , LI Yan, LIU Jian, et al. DOA Estimation of Noncircular Signals with Multistage Wiener Filter and Polynomial Rooting[J]. Journal of University of Electronic Science and Technology of China,2013,42(1):53-57.

(编辑：刘 勇)

Blind separation of radar signals based on detection of time frequency single source point

WENG Guoxiu1, XU Xuehong2

(1. Center of Education Technology, YuLin Normal University, Yulin 537000, P.R. China; 2. School of Information and Electronic Engineering, Henan University of Animal Husbandry and Economy, Zhengzhou 450044, P.R. China)

A blind separation algorithm based on detection of time frequency is proposed in this paper, in order to solve the problems of underdetermined radar signal sorting. The innovation point of this algorithm is that it shifts radar signals from time zone to time frequency zone then analyzes them. Firstly, single source point of each radar source signal was detected, Then the mixing vector in the corresponding single source point set was estimated by Singular Value Decomposition (SVD), Finally the mixing matrix simultaneously were estimated by the cluster validation technique based on k-means clustering algorithm, and the radar signals can be got by the mixing matrix and the observed signals. The proposed method can solve the problem of radar signals sorting in underdetermined condition and has considerable applicantion value for military use. The simulation experiments prove the feasibility and superiority of the algorithm.

time-frequency transformation; single source point; radar signal; cluster validation; blind separation

10.3979/j.issn.1673-825X.2017.01.007

2016-01-18

2016-10-02 通讯作者：翁国秀 wengguoxiu_2015@126.com

TN911.7

A

1673-825X(2017)01-0042-07

翁国秀(1976-)，女，广西玉林人，工程师，硕士，研究方向为计算机网络与网络安全。E-mail：wengguoxiu_2015@126.com。

徐学红(1976-)，女，河南南阳人，讲师，硕士，研究方向为智能控制。