一种低错误平层LDPC码构造方法

袁建国，汪 哲，高文春，吴英冬，郭 乔，胡潇月

(重庆邮电大学 光通信与网络重点实验室，重庆 400065)

一种低错误平层LDPC码构造方法

袁建国，汪 哲，高文春，吴英冬，郭 乔，胡潇月

(重庆邮电大学 光通信与网络重点实验室，重庆 400065)

针对低密度奇偶校验 (low-density parity-check, LDPC)码在高信噪比区域可能存在错误平层的缺点，提出一种具有低错误平层LDPC码的新颖构造方法。在该方法中，基本矩阵由渐进边增长(progressive edge growth, PEG)算法搜索构造，通过在基本矩阵相应的Tanner图中增加校验节点，并将其与拥有最小额外信息度(extrinsic message degree, EMD) 短环的变量节点相连来增大短环的连通性。另外，提出了一种基于伽罗华域的循环移位系数矩阵设计方案，无需计算机搜索即可完全避免4环的出现，降低算法复杂度。为了对该方法的可行性进行验证，分别对变量节点的度分布是规则和非规则的基本矩阵进行改进，在高斯白噪声(additive white gaussian noise, AWGN)信道下，采用置信传播(belief propagation, BP)迭代译码算法对改进后的码型进行仿真分析，仿真结果表明，利用该法所构造的码型可有效改善在高信噪比区域的错误平层。

渐进边增长(PEG)算法；额外信息度(EMD)；低密度奇偶校验(LDPC)码；错误平层

0 引 言

低密度奇偶校验码(low density parity check，LDPC)在数字存储系统和无线通信系统等领域有着广泛的应用前景，因其具有灵活的构造方法、逼近Shannon极限的优秀性能而成为信道编码领域研究的热点[1-3]。绝大多数中等码长的LDPC码都存在错误平层问题，即到了一定的高信噪比区域，误码率性能曲线突然变得平坦起来[2-3]。近年来，很多改善错误平层的方法被提出，其中包括对已有校验矩阵进行环提升、消除陷阱集/停止集，或用额外信息度(extrinsic message degree，EMD)/近似外信息度(approximate cycle EMD，ACE)为度量直接构造校验矩阵[4-5]。

针对LDPC码的错误平层问题，并考虑到参数的灵活设置和硬件的易实现性，将随机构造法与结构化构造法相结合，提出一种具有低错误平层的准循环LDPC码构造方法。首先，利用渐进边增长(progressive edge growth，PEG)算法构造基本矩阵，并对基本矩阵中短环的连通性进行改进。然后，基于伽罗华域设计循环移位系数，用此移位系数矩阵对改进后的基本矩阵进行循环扩展，最终得到校验矩阵H。仿真结果表明，本文所构造的LDPC码型可有效降低错误平层。

1 经典PEG算法

PEG算法是一种经典随机构造法[5]。其构造的核心思想是在满足度分布的条件下，利用贪心算法不断添加校验节点与变量节点之间的边。在构造校验矩阵的过程中，采用密度进化算法，选取合适的度分布，可生成任意码长和码率的LDPC码，其节点的度分布如(1)式所示。

(1)

(1)式中：dv表示与变量节点相连的最大边数；dc表示与校验节点相连的最大边数。虽然PEG算法在添加新边时能够保证最大围长，但是其不能从全局的角度对Tanner图中的环结构进行优化，所以会导致环结构比较复杂，特别是在长码长时，环存在严重的交织问题，有大量公共节点，在一定程度上会降低迭代译码性能。

2 一种低错误平层LDPC码的新颖构造方法

2.1 对基本矩阵短环EMD值的提升

在迭代译码算法中，信息传递的路径就是环，单纯地追求消环并不能有效改进LDPC码的性能，并不是环长越小对译码性能的影响就越大，反而环长较大但与剩余图连通性很差的环对译码性能的影响要远大于环长较小但与剩余图连通性较好的环。因此，剩余Tanner图中校验节点的连通性是影响译码性能的重要因素[6]。TIAN Tao在文献[7]中也指出并不是Tanner图中所有环都会对迭代译码收敛有影响，其主要取决于环的连通性。对于环的连通性可用EMD度量，有如下定理。

定理1 若一个校验节点仅与某变量节点集合连接一次，则这个校验节点称为该变量节点集合的外节点。变量节点集合的外节点个数称为该变量节点集合的EMD值[8]。

在分析短环的EMD时，可以把与构成短环的变量节点集合相连的校验节点分为3个部分：①构成短环校验节点；②与变量节点集合相连一次的校验节点；③剩余与变量节点集合相连的校验节点。其中与变量节点集合相连一次的校验节点的个数即为短环的EMD值。

另外，增大环的外部信息节点，可以有效减少小陷阱集/停止集，从而改善在高信噪比区域译码所出现的错误平层。针对PEG算法所构造的基本矩阵，为了提升其短环的EMD值，增大环的连通性，本文提出了如下算法。

初始化：根据对码长、码率的要求，设定基本矩阵的大小为(m,n)，新增一个校验节点c1。

步骤1 对基本矩阵进行全局搜索，找出其中所有的短环并计算出EMD值，每搜索到一个短环，将该短环的所有变量节点及其EMD值记录到列表φ中。

步骤2 找出φ中拥有最小EMD值的所有行，记录为φ，并找出φ中出现次数最多的变量节点νi。

步骤3 将变量节点νi与新增的校验节点c1相连，并进行判断，如果构成4环，则选择φ中的次优变量节点。

步骤4 置空φ和φ，重复步骤1-步骤3，终止条件即新增校验节点与变量节点相连的边数接近校验节点的平均度分布，或者没有满足条件的变量节点。

对改进后的基本矩阵进行搜索分析，虽然围长大于4的短环数量有少量的增加，但与新增校验节点相连的变量节点所构成短环的EMD值有显著的提升，且其包括新增的短环。因此，基本矩阵中短环的连通性得到了显著的改善。在算法复杂度上，计算环EMD值比计算环的ACE要复杂，但循环扩展的基本矩阵选取的都为短码长，因此不会存在过高复杂度。

2.2 循环移位系数和校验矩阵的设计

在构造准循环LDPC码时，基本矩阵决定了整体的度分布，但索引矩阵P的合理设计也是构造校验矩阵的关键，索引矩阵的设计直接影响校验矩阵的环长以及稀疏性。下面给出了一种基于伽罗华域的循环移位系数矩阵构造方法。

GF(q)即二元伽罗华域，其中令q=2p，p为正整数，α为伽罗华域GF(q)的本原元[9]，对于αi∈GF(q)，0≤i≤q-2，GF(q)的乘群可由集合{α0,α1,…,αq-2}构成。基于伽罗华乘群的循环移位系数矩阵P的构造如下。

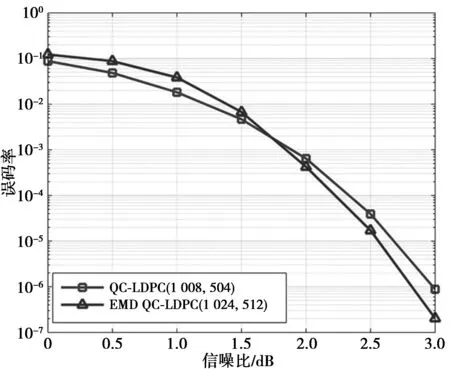
1)在P的构造中，其列单元可用乘群{(α0)-1,(α1)-1,…,(αi)-1}表示，其行单元可用乘群{α0,α1,…,αj}表示，其中0≤i,j

2)将上述行与列在二元伽罗华域中对应相乘，得到移位系数矩阵P中的每个元素为wi,j=(αi)-1αj。

3)并对P中的每个元素wi,j都对应减去α0，得到移位系数矩阵中的每个元素为wi,j=(αi)-1αj-1。

P矩阵可以保证每行(列)中的所有元素均是GF(q)中的不同元素，且不同的2行(列)的每个对应位置元素均不同。

根据要求从移位系数矩阵P中取出大小为m×n的索引矩阵，对于矩阵P中包含的-Inf元素用1替换，包含的0元素用q替换。用基本矩阵与索引矩阵相与后得到循环移位矩阵为

(2)

将循环移位矩阵中的0元素，扩展成q-1阶零矩阵，将非零元素扩展成q-1阶单位矩阵，并按其对应的移位系数进行循环移位，最终得到((m×(q-1)),(n×(q-1)))维校验矩阵H。

3 性能仿真分析

初始构造的原始基本矩阵(m,n)和待改进基本矩阵(m,n-1)的变量节点的度分布规则，令dv=3，m=24,n=48，q=24和q=26，利用移位系数矩阵对基本矩阵进行循环扩展，得到2个码率为0.5的准循环LDPC(QC-LDPC)码，即QC-LDPC(720,360)码和QC-LDPC(3 024,1 512)码。在高斯白噪声(additive white gaussian noise, AWGN)信道下，经过二进制相移键控 (binary phase shift keying，BPSK)调制，采用置信传播译码算法进行30次迭代[10]，得到其仿真性能曲线如图1所示。

图1 QC-LDPC(720,360)码与QC-LDPC(3 024,1 512)码改进前后的误码性能比较Fig.1 Comparison of the error-correction performance for QC-LDPC(720,360) and QC-LDPC(3 024,1 512) before and after improved

将图1中的仿真性能曲线进行对比分析可知，对基本矩阵改进前后所构造的QC-LDPC(720,360)码在信噪比为3.2 dB时，其纠错性能有接近一个数量级的提升。由于码长越长其纠错性能越好，改进后的QC-LDPC(3 024,1 512)码在信噪比为2.2 dB时，其纠错性能提升超过一个数量级。因此，可以验证本文所提出的方法能够有效改善LDPC码在高信噪比区域所出现的错误平层现象。

为进一步对上述提出的方法进行论证，本文对非规则的基本矩阵进行改进，设定其度分布λ(x)=0.383 54x+0.042 37x2+0.574 09x3，大小为m=31,n=64，q=25，利用本文提出的算法对基本矩阵进行改进，选取16×16的移位矩阵进行循环置换后得到EMD QC-LDPC(1 024,512)码型，在与文献[11]相同的仿真环境下，得到其纠错性能曲线如图2所示。

在码长相近和码率相同的情况下，对图2中的仿真性能曲线进行对比，会发现在信噪比为3 dB时，文献[11]构造的QC-LDPC(1 008,504)码的误码率为8.84×10-7，而本文构造的EMD QC-LDPC(1 024,512)码的误码率为2.03×10-7。因此，利用本文方法所构造的码型能够有效降低其错误平层。

4 结 论

本文针对LDPC码在高信噪比区域所存在错误平层的缺陷，提出了一种增大校验矩阵中短环EMD值的算法，通过提升短环的连通性来改善其纠错性能。另外，还设计出一种基于伽罗华域的循环移位系数的选择方案，无需计算机搜索即可有效避免4环的出现，降低其算法复杂度。仿真结果表明，利用本文提出的构造方法所构造的LDPC码型，可有效降低其在高信噪比区域的错误平层。

图2 EMD QC-LDPC(1 024,512)码与QC-LDPC(1 008,504)码的纠错性能对比图Fig.2 Comparison of the error-correction performance for EMD QC-LDPC(1 024,512) and QC-LDPC(1 008,504)

[1] FOSSORIER M P C. Quasi cyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE Transactions on Information Theory, 2004, 50(8): 1788-1793.

[2] LI Juan, LIU Keke, LIN Shu, et al. Algebraic Quasi-Cyclic LDPC Codes: Construction, Low Error-Floor, Large Girth and a Reduced-Complexity Decoding Scheme[J]. IEEE Transactions on Communications, 2014, 62(8): 2626-2637.

[3] 袁建国,周光香.光通信中基于有限域的一种QC-LDPC码构造方法分析[J].半导体光电，2015,36(4):615-617. YUAN Jianguo, ZHOU Guangxiang. Analysis on a Construction Method of QC-LDPC Codes Based on the Finite Field for Optical Communications[J]. Semiconductor Optoelectronics, 2015, 36(4):615-617,656.

[4] KHAZRAIE S, ASVADI R, BANIHASHEMI A. A PEG construction of finite-length LDPC codes with low error floor[J]. IEEE Communications Letters, 2012, 16(8): 1288-1291.

[5] HU Xiaoyun, ELEFTHERIUS E, ARNOLD D M. Regular and irregular progressive edge-growth tanner graphs[J]. IEEE Transactions on Information Theory, 2005, 51(1): 386-398.

[6] HAN Guojun, GUAN Yongliang, KONG Lingjun. Construction of Irregular QC-LDPC Codes via Masking with ACE Optimization[J]. IEEE Communications Letters, 2014, 18(2): 348-351.

[7] TIAN Tao, JONES C R, VILLASENOR J D, et al. Selective avoidance of cycles in irregular LDPC code construction[J]. IEEE Transactions on Communications, 2004, 52(8): 1242-1247.

[8] VUKOBRATOVIC D, SENK V. Transactions papers evaluation and design of irregular LDPC codes using ACE spectrum[J]. IEEE Transactions on Communications, 2009, 57(8): 2272-2279.

[9] YUAN Jianguo, XU Liang, TONG Qingzhen. A Novel QC-LDPC Code Based on the Finite Field Multiplicative Group for Optical Communications[J]. Optoelectronics Letters, 2013, 9(5): 378-380.

[10] MENG Jin, YANG Enhui. Interactive Encoding and Decoding Based on Binary LDPC Codes With Syndrome Accumulation[J]. IEEE Transactions on Information Theory, 2013, 59(5): 3068-3103.

[11] 张轶,达新宇,苏一栋.利用等差数列构造大围长准循环低密度奇偶校验码[J].电子与信息学报, 2015, 37(2): 394-398. ZHANG Yi, DA Xinyu, SU Yidong. Construction of Quasi-cyclic Low-density Parity-check Codes with a Large Girth Based on Arithmetic Progression[J].Journal of Electronics & Information Technology,2015,37(2):394-398.

(编辑：田海江)

A construction method of LDPC codes with the low error floor

YUAN Jianguo, WANG Zhe, GAO Wenchun, WU Yingdong, GUO Qiao, HU Xiaoyue

(Key Laboratory of Optical Communication and Networks, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R.China)

Considering that low density parity check (LDPC) codes may exist the fault of the error floor in the high signal noise ratio (SNR) region, a construction method of LDPC codes with the low error floor was proposed. In the proposed method, a basic matrix is constructed and searched by the progressive edge growth (PEG) algorithm, and the connectivity of the short cycle can be effectively increased by way of adding the new check nodes of the corresponding Tanner diagram in the basic matrix and connecting them with the variable nodes of the short cycle which has the minimum extrinsic message degree (EMD) value. In addition, a novel cyclic shift coefficient matrix scheme based on the Galois field method was presented, which can avoid the phenomenon of the girth-4 without the computer search, thus the algorithm complexity is reduced. In order to verify the feasibility of this construction method, the basic matrixes with the regular and irregular degree distributions of the variable nodes are improved respectively. The improved codes are simulated and analyzed under the addictive white gaussian noise(AWGN) channel and the belief propagation(BP) decoding algorithm. The simulation result shows that the LDPC codes constructed by the proposed method can effectively reduce the error floor in the high signal noise ratio region.

progressive edge growth(PEG) algorithm; extrinsic message degree(EMD); low-density parity-check(LDPC) codes; error floor

10.3979/j.issn.1673-825X.2017.01.003

2015-11-10

2016-12-20 通讯作者：袁建国 yyyyjg@126.com

国家自然科学基金项目(61472464)；重庆市基础与前沿研究计划项目(cstc2015jcyjA0554)；2016年重庆邮电大学大学生科研训练计划项目(A2016-61)

Foundation Items：The National Natural Science Foundation of China (61472464); The Natural Science Foundation of Chongqing Science and Technology Commission (cstc2015jcyjA0554); The Undergraduate Science Research Training Project for Chongqing University of Posts and Telecommunications (A2016-61)

TN911.22

A

1673-825X(2017)01-0015-04

袁建国(1968-)，男，重庆人，教授，博士，硕士生导师，主要研究方向为通信技术与信道编码技术。E-mail: yyyyjg@126.com。

汪 哲(1992-)，女，重庆人，硕士研究生，主要研究方向为通信系统中FEC编译码技术。 E-mail: 578091834@qq.com。

高文春(1989-)，男，内蒙古赤峰人，硕士研究生，研究方向为通信技术与信道编码技术。E-mail: gaowencun@ict.ac.cn。