移动流量特征模型研究与分析

许 朝，谢人超，黄 韬，刘 江，张云勇

(1.北京未来网络科技高精尖创新中心，北京 100124；2.北京邮电大学 网络与交换国家重点实验室，北京 100876；3.中国联合网络通信集团有限公司研究院，北京 100032)

移动流量特征模型研究与分析

许 朝1，2，谢人超1，2，黄 韬1，2，刘 江1，2，张云勇3

(1.北京未来网络科技高精尖创新中心，北京 100124；2.北京邮电大学 网络与交换国家重点实验室，北京 100876；3.中国联合网络通信集团有限公司研究院，北京 100032)

不断增加的移动数据流量给运营商的网络带来了前所未有的挑战，因此，准确地表示网络流量特征对于合理规划网络结构和配置网络资源有着重要意义。主要介绍移动网络流量特征模型，并对现网数据进行分析，得出网络流量概率密度服从对数正态分布，在未来网络架构的设计中可作为数据输入模型，用于网络进行仿真和性能验证。

移动网络；流量分布；流量模型；流量概率密度

0 引言

随着通信技术的发展和用户需求的不断提高，越来越多的移动业务和应用场景不断涌现，使得移动网络流量呈现出爆炸式的增长。同时，智能终端的普及以及可穿戴设备、智慧城市、智慧家居、数字健康、机器通信(Machine-to-Machine，M2M)等业务的出现，也加剧了网络流量增长。Cisco公司的统计预测数据表明，预计到2020年，智能手机流量将超过PC端流量，占总流量的30%；电视、平板电脑、智能手机和M2M(machine-to-machine)产生的流量将分别以17%、39%、58%和44%的年复合增长率增长；Wi-Fi和移动设备产生的IP流量将占总流量的66%[1]。

网络流量的增长速度，特别是视频流量的增长,远远超过了摩尔定律和路由性能提升的速度，为应对这种情况，各个组织、地区与国家已经启动了第五代移动通信(5G)网络的研究，诸如欧盟的METIS项目与5GPPP合作研究项目、中国IMT-2020(5G)推进组，国际电信联盟的ITU-R2020工作组以及韩国的5G论坛等。同时，中国移动、西班牙电信、AT&T、华为、爱立信与阿尔卡特朗讯等运营商与设备商也先后发布了5G白皮书和技术研究报告，业界关注的重点主要从网络架构、技术创新以及业务应用场景等方面开展研究。

无论是工业界还是学术界的研究人员都越来越意识到现网数据分析的重要性，并将数据的建模和分析结果用于网络优化和下一代网络的设计当中[2]。因此，对于移动网络流量特征的提取和分析成为网络规划和设计中的重要参考因素。本文将重点介绍当前主要的移动网络流量特征模型，并对现网流量进行分析，验证符合实际网络流量的特征模型，最后对研究内容做简单总结。

1 流量特征模型

不断增加的移动数据流量给运营商的网络带来了巨大的挑战，因此，准确地表示网络流量特征对于合理规划网络结构和配置网络资源有着重要意义。目前，流量特征模型包括空间泊松点过程模型、对数正态分布模型、指数分布模型、高斯分布模型以及离散余弦变换模型等。本节将主要介绍以上几种模型。

1.1 空间泊松点过程模型(Spatial Poisson Point Process，SPPP)

SPPP主要应用于基站的位置建模和分析用户位置的随机特性，其中，均匀SPPP模型是蜂窝网络分析中常见的随机几何模型，该模型中用户分布服从均匀分布，是最简单而且在仿真研究中使用最为广泛的模型之一。均匀SPPP模型能够很好地反映相互独立条件下随机点的分布情况。

假设SPPP强度为λ，B={B1,B2…Bk}是互不相交的Borel集，N(B)={N(B1),N(B2)…N(Bk)}是独立随机变量，用来表示在任何有界的Borel集B中点的数量。某个区域中用户数量可表示为：

(1)

式中，A(B)表示区域，在区域A(B)中N(B)服从强度为λA(B)的泊松分布。在Borel集B中存在k个点的概率可表示为：

(2)

由于实际用户分布并不服从均匀分布，均匀SPPP分布无法表示用户分布的随机性。与均匀SPPP不同，非均匀SPPP用来描述某个区域的聚集现象，在Borel集B中存在k个点的概率可表示为：

(3)

为表示用户的非均匀分布，文献[3]基于均匀SPPP分布提出了修正的Matern模型，在该模型中，首先生成一个均匀SPPP分布的集群中心，然后以集群中心的每个点为圆心，以预设值r为半径的范围内生成用户位置，这些用户分布服从均匀SPPP分布。其中，预设值r以及每个集群中平均用户数需要预先确定以保证整体的用户密度和均匀分布中一致。

在小区非空闲状态，均匀用户分布概率(PH)可用式(4)表示，非均匀用户分布概率(PI)可用式(5)表示：

(4)

PI≈1-e-(1-e-ρR2π)，

(5)

式中，R为小区的半径，r为集群中心的预设半径，ρ为用户密度。

此外，文献[4]分别对密集城区、普通城区以及郊区3个地区做了研究，结论表明SPPP模型只适用于普通城区和郊区，而密集城区则用Matern模型更为合适。

1.2 对数正态分布模型(LogNormalDistributionModel)

如果随机变量的对数服从正态分布，那么随机变量就服从对数正态分布。文献[5]通过对现网数据的测量和分析表明：流量密度可用对数正态分布近似表示。由于流量分布在时间和空间上的不固定性，文献还分析了流量在空间上的相关性，并结合对数正态分布提出了一种空间流量模型。

该模型中，区域被划分为M×N个像素区域，给定像素区域gm,n(m=1,2…M,n=1,2…N)的流量密度为ρm,n/(bytes/km2)，假设ρ=(ρm,n)m-1…M;n-1…N表示流量密度矩阵，xm,n,ym,n为二维笛卡尔坐标，生成高斯随机分布矩阵：

(6)

式中，和il、jl为(0,ωmax)之间的均匀随机变量，ωmax用来决定随机波动率，φl、ψl为(0,2π)之间的均匀随机变量。得到式(6)之后，可根据式(7)生成对数正态分布矩阵。通过控制σ、μ可调节ρ的大小，使之与特定区域的流量密度相符。

(7)

此外，文献[6]对E-Plus在德国某个城市的流量数据分析之后指出，这些数据得到的流量密度并不服从均匀分布。Gotzner和Michalopoulou的研究表明，在一段特定的时间内，不同2G小区中的语音业务量可以用对数正态分布来描述[6]，并且在不同小区中GPRS和EDGE的数据流量可以用混合的对数正态分布来近似表示[7]。

1.3 指数分布模型(Exponential Distribution Model)

文献[8]对不同地区蜂窝网络流量数据进行了分析结果表明，随着与市区中心距离的增大，流量密度以指数形式递减。对市中心流量密度经行归一化之后，流量密度可表示为：

p(d)=e-d/k，

(8)

式中，d为距离市中心距离，单位为km，k为递减参数，且随着地理位置的不同而不同。但需要注意的是，指数模型只适用于城区，并不具有普适性，无法反应流量密度与距离的关系。因此，在流量的空间分布上，文献[8]使用了指数线性模型式(9)和分段线性模型式(10)对不同地区的流量密度进行了研究，结果表明，这2种模型相对于指数模型来说更能反应流量密度与距离的关系，其中C和D为常数。

(9)

(10)

1.4 高斯分布模型(Gaussian distribution model)

二维高斯分布模型可近似表示移动蜂窝网络中用户的分布情况，用户密度可表示为：

(11)

式中，(x,y)为用户位置，η可通过对比实验仿真结果来确定，根据每个小区，可动态调整均值μ1、μ2和标准差σ1、σ2，生成包括均匀分布和非均匀分在内的适用范围更广的分布模型。

文献[9]使用二维高斯分布模型模拟移动网络中的用户分布情况，研究了各个参数取不同值时对网络容量的影响。通过文献[10]中的方法计算小区间的平均干扰和反向链路容量，并与文献[11]中的模型进行了对比，结果表明使用高斯分布模型对于大型WCDMA网络的规划速度更快，准确度更高。

1.5 离散余弦变换模型(DiscreteCosineTransformModel)

文献[12]对国内某地区一周的的现网流量做了研究，通过对密集城区、普通城区和郊区三种区域流量特征的分析提出了截断二维离散余弦变换模型，其表达式如下：

(12)

具体参数含义如表1所示。

表1 截断二维离散余弦变换模型参数含义

1.6 模型对比

从前文的介绍可以看出不同的模型具有不同的适用范围和特征，具体区别如表2所示。

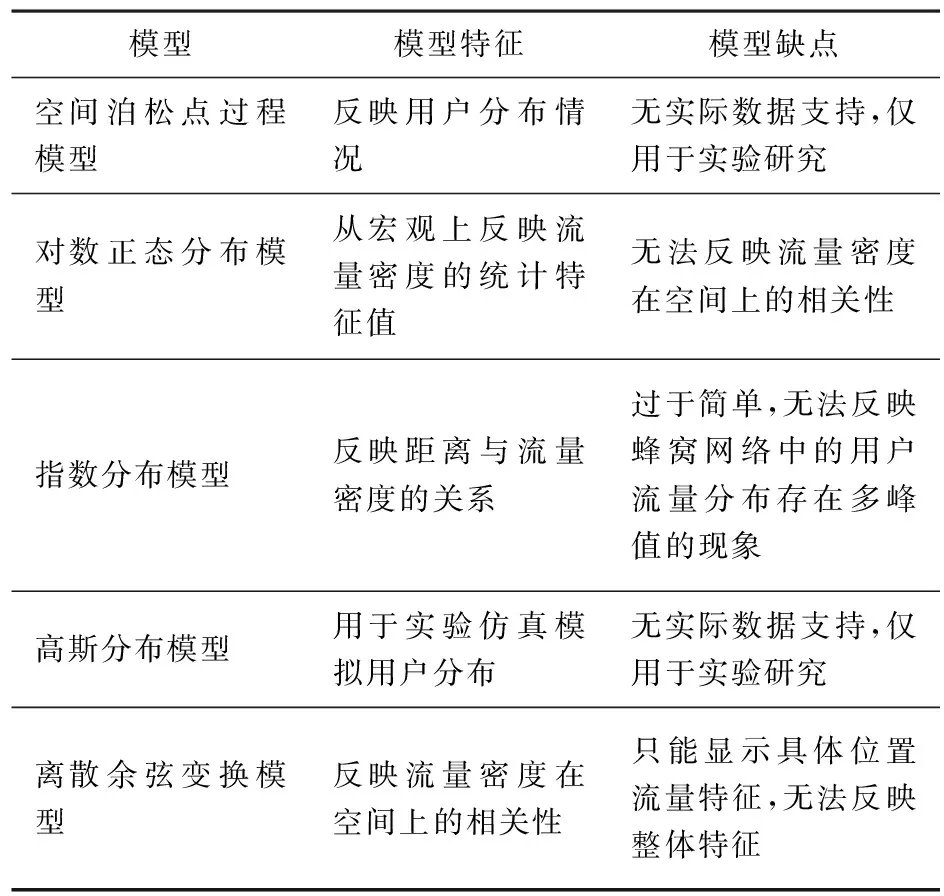
表2 流量特征模型对比

2 数据分析

本文采集了国内某运营商在某市一周的移动网络流量数据，地理位置涵盖整个城市，包括67 610个基站的流量数据及经纬度地理坐标。采用网格化的方法将所在地区分为面积相等的小网格，每个网格的面积是0.009 550 8 km2，同一区域中的各个基站流量大小相加作为本区域整体的流量大小，并假设网格内流量均匀分布。由于地理分布上不是一个规则的矩形，本文用MATLAB中的nonzeros函数来去除掉无效区域，得到图1所示的网络流量概率密度分布图，该图描绘了平均流量密度的分布情况。

图1 整体网络流量密度概率分布

结果显示对数正态分布与数据最为吻合，拟合函数如下：

(13)

拟合函数中SSE(方差和)取值为0.000 017 38，接近于0；相关系数为0.999 9，接近于1，整体拟合效果较为理想，拟合参数如表3所示。

表3 拟合参数

在对该地区选取的住宅区、商业区和办公区3个区域进行同样的分析之后得到图2、图3和图4的结果。

仿真分析表明这3个地区流量概率密度均服从对数正态分布。因此，无论是整体流量密度还是局部流量密度均可用式(14)表示，通过调节N可得到不同的流量特征。

(14)

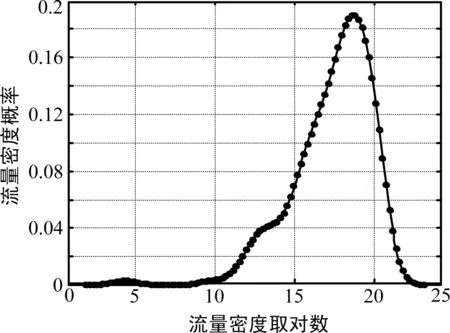
图2 住宅区流量密度概率分布

图3 商业区流量密度概率分布

图4 办公区流量密度概率分布

3 结束语

本文主要对主要的移动网络流量特征模型做了简单介绍，并对不同模型的适用范围和缺点作了总结和对比。通过对现网数据的处理和分析，得到了符合实际的移动网络流量特征模型。

结果表明，无论是整体流量概率密度还是局部流量概率密度，均服从对数正态分布。因此在未来网络设计中进行数据验证时可采用对数正态分布模型模拟网络流量，从而验证网络相关性能是否满足设计要求，对于未来网络的规划和设计都具有重要意义。

[1] Cisco Visual Networking Index: Forecast and Methodology,2015-2020.[DB/OL].http:∥www.cisco.com/c/dam/en/us/solutions/collateral/service-provider/visual-networking-index-vni/complete-white-paper-c11-481360.pdf.

[2] 周 轩.下一代移动通信网络中的业务特征认知及服务机制研究[D].杭州：浙江大学,2015.

[3] Vidacs A,Godor I.Power Saving Potential in Heterogeneous Cellular Mobile Networks[C]∥Personal,Indoor and Mobile Radio Communications(PIMRC).IEEE,2011:2412-2414.

[4] Zhang J,Wang W,Zhang X,et al.Base Stations from Current Mobile Cellular Networks: Measurement,Spatial Modeling and Analysis[C]∥Wireless Communications and Networking Conference Workshops (WCNCW).IEEE,2013:1-5.

[5] Lee D,Zhou S,Zhong X,et al.Spatial Modeling of the Traffic Density in Cellular Networks[J].IEEE Wireless Communications,2014,21(1): 80-88.

[6] Gotzner U,Rathgeber R.Spatial Traffic Distribution in Cellular Networks[C]∥Proc.VTC,1998,3(5)：1994-1998.

[7] Michalopoulou M,Riihijarv J,Mahonen P.Towards Characterizing Primary Usage in Cellular Networks: A Traffic-based Study[C]∥New Frontiers in Dynamic Spectrum Access Networks(DySPAN).2011 IEEE Symposium,2011: 652-655．[8]AlmeidaS,QueijoJ,CorreiaLM.SpatialandTemporalTrafficDistributionModelsforGSM[C]∥Proc.IEEEVTS50thVehicularTechnologyConference,1999,1(9):131-135.

[9]SonN,RobertA.ApproximatingUserDistributionsinWCDMANetworksUsing2-DGaussian[C]∥InternationalConferenceonComputing,CommunicationsandControlTechnologies,2005：1-5.

[10]AklR,HegdeM,Naraghi-PourM,etal.Multi-cellCDMANetworkDesign[C]∥IEEETransVehTechnol,2001,50(5):711-722.

[11]AklR,ParvezA.ImpactofInterferenceModelonCapacityinCDMACellularNetworks[C]∥ProceedingsofSCI04:CommunicationandNetworkSystems,TechnologiesandApplications,2004,3(7):404-408.

[12]GuanL,ZhangX,LiuZ,etal.SpatialModelingandAnalysisofTrafficDistributionBasedonRealDatafromCurrentMobileCellularNetworks[C]∥IEEE,2013：135-138.

Research and Analysis of Mobile Traffic Model

XU Chao1，2,XIE Ren-chao1，2,HUANG Tao1，2,LIU Jiang1，2,ZHANG Yun-yong3

(1.Beijing Advanced Innovation Center for Future Internet Technology,Beijing 100124;2.Beijing University of Posts and Telecommunications,Beijing 100876;3.China Unicom Research Institute,Beijing 100032)

Increasing mobile traffic has brought great challenges to the operators’ network.It is significant to describe the features of traffic accurately fornetwork structure design and network resources configuration.In this paper,several mobile spatial traffic modelsare introduced and real network traffic data is analyzed.Result shows that the traffic probability density follows lognormal distribution which can be used as the input data model in future network designfornetwork simulation and performance validation.

mobile network;traffic distribution;traffic model;traffic probability density

10.3969/j.issn.1003-3114.2017.01.02

许 朝，谢人超，黄 韬，等.移动流量特征模型研究与分析[J].无线电通信技术,2017,43(1):07-10,22.

2016-09-02

国家高技术研究发展计划(863计划)项目(2015AA016101)；国家自然科学基金项目(61501042)；北京市科技新星计划项目(Z151100000315078)；北京邮电大学青年科研创新计划专项(2015RC10)

许 朝(1993—)，男，硕士研究生，主要研究方向：未来网络关键技术、内容中心网络、网络缓存等。张云勇(1976—)，男，博士后，中国联通研究院副院长，北京邮电大学兼职教授，主要研究方向：云计算、移动互联网、融合网络技术等。

TN915

A

1003-3114(2017)01-07-4