NTRU型无需密钥交换的全同态加密方案

宋新霞，陈智罡，周国民

（1. 浙江万里学院基础学院，浙江 宁波 315100；2. 浙江万里学院电子与计算机学院，浙江 宁波 315100；3. 浙江警察学院计算机与信息技术系，浙江 杭州 310053)

NTRU型无需密钥交换的全同态加密方案

宋新霞1，陈智罡2，周国民3

（1. 浙江万里学院基础学院，浙江 宁波 315100；2. 浙江万里学院电子与计算机学院，浙江 宁波 315100；3. 浙江警察学院计算机与信息技术系，浙江 杭州 310053)

详细分析了环LWE上NTRU基本加密方案的噪声特性与同态性，引出了“零次同态加密”的概念，并且说明了环LWE上NTRU基本加密方案是一个零次同态加密。提出了2个同态加密方案，展示了如何基于NTRU零次同态加密，设计NTRU型BGN同态加密方案与全同态加密方案。在该NTRU型全同态加密方案中，其密钥在密文计算中始终保持不变，因此，无需密钥交换就获得了一个全同态加密方案。此外，该NTRU型全同态加密的密文是一个向量，相比密文是矩阵的GSW全同态加密方案，具有存储与传输上的优势。

全同态加密；NTRU加密；环LWE问题；密钥交换；BGN同态加密

1 引言

全同态加密能够在不知道密钥的情况下，对密文进行任意计算，这种特殊的性质使全同态加密有广泛的应用需求。同态加密的概念自 1978年提出后[1]，一直是密码学界的开放难题，直到2009年Gentry提出第一个全同态加密方案[2]。随后人们基于不同的困难问题，设计出一些全同态加密方案，如小数理想上的全同态加密方案[3]、整数上的全同态加密方案[4～6]、LWE（环LWE）上的全同态加密方案[7～12]。在这些全同态加密方案中，由于环 LWE上的全同态加密方案简单、效率高，安全性被归约到格上标准困难问题，并且被认为具有抗量子攻击的特性，所以成为目前主流的全同态加密方案。

目前，环 LWE上的全同态加密方案所基于的基本公钥加密方案[13,14]及其变形[7]，其本身具有加法同态属性，但不具有乘法同态属性。为了使密文能够进行乘法计算，定义密文乘积形式为张量密文c1⊗c2，对应的密钥是s⊗s。尽管这样定义能够使密文进行乘法计算，但这导致了密文和密钥的维数膨胀，如果不对维数约减的话，将进行不了几次乘法。为此，文献[7]引入了密钥交换技术，通过密钥交换可以将维数膨胀的密文转换成一个正常维数的新密文，对应的密钥是一个正常维数的新密钥。可以说，密钥交换技术导致了环 LWE上全同态加密方案的诞生，但密钥交换也是需要付出代价的。

一方面，每次密文乘法计算后，都要将乘积密文与密钥交换矩阵相乘，从而进行密钥交换得到一个正常维数的密文，极大地影响了计算效率；另一方面，密钥交换矩阵是公钥，对一个深度为L的全同态加密方案，在公钥中需要包含L个密钥交换矩阵。在环 LWE的全同态加密方案下，每个密钥交换矩阵是的矩阵，密钥交换矩阵的尺寸是，而在LWE的全同态加密方案下，每个密钥交换矩阵是的高维矩阵，密钥交换矩阵的尺寸是 (n + 1)3log2q。可见，密钥交换矩阵占用了大量空间。因此，如何去除密钥交换过程是全同态加密研究中一个非常重要的问题。

一个自然的想法就是如果密文是多项式，则多项式的乘积不会引起密文维数的增长。环LWE上的NTRU加密方案的密文是一个多项式，本文首先分析了该方案的噪声特性与同态性，引出了“零次同态加密”的概念，说明NTRU加密方案是一个“零次同态加密”，即密文乘积 c1·c2本身具有潜在的乘法同态性，但由于噪声增长依赖于密文c1的长度，导致密文乘积噪声过大而丧失了乘法同态性。此外，密钥在密文乘积中是保持不变的。这与先前的张量积形式构造的全同态加密方案是不同的。

为了约减噪声，本文将密文c1的系数展开成位的形式，同时为了获得同态性，将密文c2从多项式“提升”到向量c2'，其中，向量中的每个元素是分别对明文2im (i=0,…,l)的加密。即向量中的第一个密文是NTRU加密的原始密文，其他密文都是为了同态性而存在的。密文乘积是行向量与列向量的乘积，即 BitDecomp(c1)·c2'，其中，BitDecomp(c1)输出的是行向量。从而构建出一个BGN加密方案，该方案具有加法同态性，但是只能够进行一次乘法计算。是因为密文乘积的结果没有提供为了同态性而存在的元素。在此基础上，将密文c1也从多项式“提升”到向量。密文进行乘积时，将向量中的每个元素展开成位的形式，形成一个矩阵，密文乘积是矩阵与向量的乘积，从而获得了乘法同态性，构造出一个全同态加密方案。

本文详细展示了如何基于NTRU零次同态加密，设计一个NTRU型BGN同态加密方案与全同态加密方案。在该NTRU型全同态加密方案中，其密钥在密文计算中始终保持不变，因此无需密钥交换就获得了一个全同态加密方案。此外，该NTRU型全同态加密的密文是一个向量，而GSW全同态加密中的密文是矩阵[10]，因此具有存储与传输上的优势。

2 预备知识

1) 基本符号

本文的向量默认为列向量。向量用小写粗体表示，矩阵用大写粗体表示。R上的元素用小写表示。( )T表示转置。令a∈R，则，其中，是多项式 a的系数，定义表示无穷范数，即多项式 a的系数的最大值。对于 a，b∈R，有

使用x←D表示x从分布D中取样。为了简单起见，定义B边界分布为从该分布取样的值不超过B。如果D是R上的B边界分布，x←D表示x是一个B边界的多项式，即

2) 环LWE问题与判定小多项式比问题

本文方案的安全性基于判定环 LWE问题和判定小多项式比问题。环LWE问题是LWE问题在环上的推广[13,14]。判定小多项式比问题参考文献[15]。

3) 全同态加密

一个同态加密方案包含 4个概率多项式算法：公钥和密钥生成算法、加密算法、解密算法、密文计算算法。具体定义参考文献[2, 7]。另外，BGN同态加密指的是具有加法同态性，但是只能够进行一次乘法的方案[16,17]。

3 NTRU型BGN同态加密方案

本节基于文献[11]提出的NTRU基本加密方案，设计一个 BGN同态加密方案，该方案具有加法同态性，但是只能够进行一次乘法同态计算。首先对NTRU基本加密方案的加密噪声和解密噪声进行分析，为后面同态加密方案的噪声分析奠定基础。

3.1 NTRU基本加密方案的噪声分析

E.SecretKeygen(1λ)：选取 f′←χ，计算f←2f′+1使f≡1(mod 2)。若f在Rq上是不可逆的，则重新选取f′。令私钥sk=f∈R。

E.PublicKeygen(sk)：选取g←χ，计算h=2g f−1∈Rq，令公钥pk=h。

E.Enc(pk, m)：消息m∈{0,1}，选取s，e←χ，输出密文c←m+hs+2e∈Rq。E.Dec(sk, c)：输出m←cf mod 2。

下面从加密噪声和解密噪声的角度说明方案的正确性，也便于下文对同态操作的噪声进行分析。

引理1 加密噪声

q, n, Rq,χ是上述加密方案的参数，令χ的上界是B。任意f′←χ，计算f←2f′+1使f ≡1(mod 2)。若 f在 Rq上是不可逆的，则重新选取 f′。任意m∈{0,1}。令h←E.PublicKeygen(f)，c←E.Enc(h, m)，则存在v且使如下等式成立

其中，v为密文的噪声。

证明 根据基本加密方案有

cf = mf + hsf + 2ef = mf + 2gs +2ef = mf + 2v∈Rq

由于χ的上界是B，所以g、s、e的系数上界是B，f的系数上界是2B+1。又可知，gs的系数上界是nB2，ef的系数上界是nB(2B+1)，所以，v的系数上界是3nB2+nB，即

引理1给出了初始密文（新鲜密文）的噪声上界。由于密文计算过程中噪声会增长，而解密的正确性与密文中噪声大小是相关的，引理2给出了密文能够正确解密的噪声界。

引理2 解密噪声

任意f, c∈Rq，且有f ≡1(mod 2)。若满足其中，m∈{0,1}，。则有

E.Dec(f, c)=cf (mod 2)=mf + 2v(mod 2) = mf (mod 2)= m

引理2说明在解密过程中，只要保持形如“mf + 2v”的解密结构，且，就能够正确解密。这种保持解密结构的思想在下文设计同态加密属性的过程中非常有用。

3.2 NTRU型BGN同态加密方案

上述NTRU基本加密方案具有加法同态性，但不具有乘法同态性。为了获得乘法同态性，本文将上述NTRU基本加密方案的密文提升成向量的形式，向量中每个元素是对如下明文的加密：m, m2,…, m2l，向量的长度是。BGN同态加密方案的参数选择和NTRU基本加密方案相同，方案如下。

6) BGN.Mult(pk, c1, c2)：令c10是密文向量c1中的第一个元素，输出BitDecomp(c10)·c2∈。注意 BitDecomp(c10)是一个行向量，其中每个元素是一个系数为0或1的多项式，而c2是一个列向量。

上述BGN方案的正确性、安全性和NTRU基本加密方案是一样的。该 BGN加密方案的乘法密文的长度非常短，只是一个多项式，与基本加密方案的密文长度相同。下面分析这2个方案的同态性。

3.3 同态性

由于上述NTRU基本加密方案和BGN同态加密方案的加法同态性是显然的，下面只关注其乘法同态性。

3.3.1 NTRU基本加密方案的同态性

令ci∈Rq(i=1,2)是用基本加密方案对明文mi∈{0,1}的加密，其对应密钥是f，有cif =mif + 2vi∈Rq，且满足。令c×= c1⋅c2，则c×f= c1⋅ ( m2f + 2v2)= m2(m1f + 2v1)+2c1v2= m1m2f +2m2v1+ 2c1v2。其中，v2和v1的系数都是小的，但是由于c是R上的密文，所以其系数的界为1q，因此密文乘积的噪声主要依赖于密文 c1的长度，由于，显然噪声值远大于，因此

令ci∈(i=1, 2)是用BGN同态加密方案对明文mi∈{0,1}的加密，其对应密钥是f，其中，c10是密文向量 c1中的第一个元素。令 c×= Bit-Decomp(c10)⋅c2，则有

由于 v10、BitDecomp(c1)和 v2都是小的，所以密文乘法可以正确解密，从而密文进行一次乘法计算。

但是如果c×再和另外一个乘法密文c×＇进行乘法计算，由于没有c×和c×＇的向量形式密文，所以按照上述乘法定义将无法计算，从而只能进密文乘积无法正确解密。所以在乘法同态计算中，由于噪声依赖于密文导致噪声值过大，从而一次乘法也无法进行。所以基本加密方案不具有乘法同态性。

这种由于噪声阻碍了同态性的获得的方案，称为零次同态加密。零次同态加密可以看成是部分同态加密（somewhat homomorphic encryption）的极端情况。

3.3.2 BGN加密方案的同态性

令c为用BGN加密方案对明文m∈{0,1}的加密，对应密钥是f。根据解密定义可知c f =(c0f, c1f,…,clf)T= (mf +fhs0+2fe0, m2f + fhs1+2fe1,…, m⋅2lf + fhsl+ 2fel)T=(m, m2,…, m2l)Tf +2v= mPowerof2(f) +2v，其中，v= gsi+eif (i=0,…,l)。注意Powerof2(f)表示的是一个列向量。行一次乘法计算。

下面构造一个NTRU层次型全同态加密方案。

4 层次型全同态加密方案

在该层次型全同态加密方案中，密钥在密文计算过程中是保持不变的，不需要密钥交换。方案如下。

1) FHE.Setup(λ, L)：输入安全参数λ和电路深度 L，输出多项式次数 n、分圆多项式φ( x) = xn+1，其中，n是2的幂次方；环上的噪声分布χ，其界为 B；素数模 q。令

2) FHE.KeyGen(λ)：选取 f’←χ，计算 f←2f’+1使f ≡1(mod 2)。若f在Rq上是不可逆的，则重新选取f’。令私钥sk=f∈R。选取g←χ，计算h=2g f-1∈Rq，令公钥pk=h。

3) FHE.Enc(pk, m)：消息m∈{0,1}，选取si，ei←χ(i=0,…,l)，输出密文向量 c=ci(i=0,…,l)，其中，ci←m2i+hsi+2ei∈Rq。

4) FHE.Dec(sk, c)：输出m← c0f mod 2。

5) FHE.Add(pk, c1, c2)：输出

6) FHE.Mult(pk, c1, c2)：输出BitDecomp(c1)⋅

下面分析该方案的安全性。

定理1 选择参数（n, χ, q）使小多项式比问题和环 LWE问题的困难性假设成立。h和hsi+2ei(i=1,…,l)如全同态加密方案所述，则分布（h，hsi+2ei）与Rq×Rq上均匀选取的元素是不可区分的。

证明 对于任意的i，根据加密算法的定义，hsi+2ei相当于对0的加密。根据文献[11]中的小多项式比问题假设，gf−1与Rq上均匀选取的元素不可区分，所以，公钥h=2gf−1也是与Rq上均匀选取的元素不可区分。又根据文献[14]中RLWE困难性的假设，hsi+2ei与Rq上均匀选取的元素不可区分，所以，密文ci与Rq上均匀选取的元素不可区分。由此证明了上述全同态加密方案的安全性。

下面从同态性和噪声约减 2个角度进行分析，从而说明上述方案的正确性。

4.1 同态性分析

由于方案的加法同态性是显然的，所以只关注其乘法同态性。

由于v1、BitDecomp(c1)和v2中的元素都是小的，根据解密算法可以正确解密。因此方案具有乘法同态性。

4.2 密文计算的噪声分析

本节对上述方案的加法和乘法的噪声进行分析，从而说明方案可以进行多项式深度的同态密文电路计算。

1) 加法噪声分析

根据方案的加法定义，令c+= c1+c2，则有

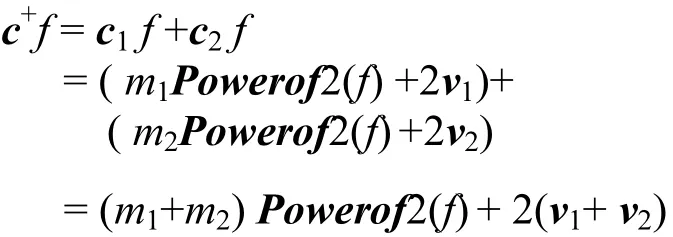
2) 乘法噪声分析

根据乘法定义，令 c×=BitDecomp(c1)⋅c2∈，则有 c×f=m1m2Powerof2(f) + 2m2v1+ 2BitDecomp(c1)⋅v2∈。令c1j是矩阵BitDecomp(c1)中的第j行向量，则c1j中有l+1个系数为0或1的多项式。另外根据≤3nB2+nB，得到≤nl(3nB2+nB)= nlE。令N=nl≈nlogq，有≤E，由此可知c×的噪声为(N+1)E。

下面分析深度为L的密文电路计算的噪声。这里只考虑乘法，因为乘法的噪声增长远大于加法的噪声增长。首先，分析深度为2的乘法电路，令1×c和2×c是经过深度为 1的乘法电路计算的结果，其噪声分别为 v1′和 v2′，由上可知≤(N+1)E。经过第2层乘法电路计算后，其结果记为，则有2BitDecomp(c1)⋅v2′。由于≤(N+1)E，所以≤N(N+1)E。另外(N+1)E，所以的噪声为(N+1)2E。以此类推，经过深度为L的电路计算，其噪声至多为(N+1)LE。只要(N+1)LE不超过，密文就能够正确解密。

4.3 乘法计算优化

在上述2个密文乘法计算中，噪声主要依赖于第一个密文（被乘数）的噪声，所以，改变乘法顺序可以优化密文计算。该事实也在文献[18]中观察到。如(i=1,…,4)是4个初始密文，每个密文中的噪声都为 E。上述电路乘法是两两相乘，即将乘积 c1c2c3c4分成 c5←c1c2和c6←c3c4，然后再计算c5c6。如果按照顺序方式乘积，首先计算c5←c1c2，再计算c6←c5c3，最后计算 c7←c6c4。根据上面的噪声分析，c5的噪声是(N+1)E，c6的噪声是(N+1)E+NE=(2N+1)E，c7的噪声是(2N+1)E+NE=(3N+1)E。以此类推，那么经过深度为L的电路计算，其噪声至多为(LN+1)E。这意味着对同样的L，经过乘法优化，q可以取为关于n的多项式，即q可以变得更小，使计算效率提高。或者说对于同样的q，电路深度L可以更深。关于全同态加密电路深度与具体参数问题可以参考文献[19～21]。

5 结束语

环LWE上的NTRU基本加密方案的密文形式非常简单，就是Rq上的一个多项式，因此其乘积形式也非常自然简单，就是2个密文多项式的乘积，但其密文乘积的噪声主要依赖于乘积中的第一个密文，所以密文乘积的噪声过大，导致一次乘法也进行不了。为了约减噪声，本文将第一个密文表示成位的形式，将第2个密文由多项式提升到向量，设计了一个环LWE上的NTRU型BGN同态加密方案。该BGN加密方案的乘法密文的长度非常短，只是一个多项式，与基本加密方案的密文长度相同。然后，将第一个密文也从多项式提升到向量形式，通过上述约减噪声的方法获得了乘法同态性。由于密文乘积是一个方阵与向量的乘积，所以密文乘积的结果还是向量，并没有导致密文乘积的膨胀，从而获得了一个无需密钥交换的全同态加密方案。本文方案与密文是矩阵的GSW全同态加密相比，具有存储与传输上的优势。

[1] RIVEST R L, ADLEMAN L, DERTOUZOS M L. On data banks and privacy homomorphisms[J]. Foundations of Secure Computation, 1978, 4(11): 169-180.

[2] GENTRY C. Fully homomorphic encryption using ideal lattices[C]//The 41st Annual ACM Symposium on Theory of Computing. 2009: 169-178.

[3] SMART N P, VERCAUTEREN F. Fully homomorphic encryption with relatively small key and ciphertext sizes[M]//Public Key Cryptography-PKC 2010. Berlin: Springer, 2010: 420-443.

[4] DIJK M V, GENTRY C, HALEVI S, et al. Fully homomorphic encryption over the integers[M]//Advances in Cryptology-Eurocrypt 2010. Berlin: Springer, 2010: 24-43.

[5] JEAN-SÉBASTIEN C, AVRADIP M, NACCACHE D, et al. Fully homomorphic encryption over the integers with shorter public keys[M]//Advances in Cryptology-CRYPTO 2011. Berlin Heidelberg: Springer, 2011: 487-504.

[6] JEAN-SÉBASTIEN C, NACCACHE D, TIBOUCHI M. Public key compression and modulus switching for fully homomorphic encryption over the integers[M]//Advances in Cryptology-Eurocrypt 2012. Berlin Heidelberg: Springer, 2012: 446-464.

[7] BRAKERSKI Z, VAIKUNTANATHAN V. Efficient fully homomorphic encryption from (standard) LWE[C]//IEEE 52nd Annual Symposium on Foundations of Computer Science, IEEE Computer Society. 2011: 97-106.

[8] BRAKERSKI Z, GENTRY C, VAIKUNTANATHAN V. (Leveled) fully homomorphic encryption without bootstrapping[C]//The 3rd Innovations in Theoretical Computer Science Conference. 2012: 309-325.

[9] BRAKERSKI Z. Fully homomorphic encryption without modulus switching from classical gapSVP[M]//Advances in Cryptology-CRYPTO 2012. Berlin Heidelberg: Springer, 2012: 868-886.

[10] GENTRY C, SAHAI A, WATERS B. Homomorphic encryption from learning with errors: conceptually-simpler, asymptoticallyfaster, attribute-based[M]//Advances in Cryptology-CRYPTO 2013. Berlin Heidelberg: Springer, 2013: 75-92.

[11] LÓPEZ-ALT A, TROMER E, VAIKUNTANATHAN V. On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption[C]//The 44th Symposium on Theory of Computing. 2012: 1219-1234.

[12] CHEN Z G, WANG J, ZHANG Z N, et al. A fully homomorphic encryption scheme with better key size[J]. China Communications, 2014, 11(9): 89-99.

[13] REGEV O. On lattices, learning with errors, random linear codes, and cryptography[C]//The 37th Annual ACM Symposium on Theory of Computing. 2005: 84-93.

[14] LYUBASHEVSKY V, PEIKERT C, REGEV O. On ideal lattices and learning with errors over rings[M]//Advances in Cryptology-EUROCRYPT 2010. Berlin Heidelberg: Springer, 2010: 1-23.

[15] STEHLÉ D, STEINFELD R. Making NTRU as secure as worst-case problems over ideal lattices[M]//Advances in Cryptology-EUROCRYPT 2011. Berlin Heidelberg: Springer, 2011: 27-47.

[16] GENTRY C, HALEVI S, VAIKUNTANATHAN V. A simple BGN-type cryptosystem from LWE[M]//Advances in Cryptology –EUROCRYPT 2010. Berlin Heidelberg: Springer, 2010: 506-522.

[17] BONEH D, GOH E J, NISSIM K. Evaluating 2-DNF formulas on ciphertexts[C]//Theory of Cryptography: Second Theory of Cryptography Conference(TCC 2005). 2005: 325-41.

[18] BRAKERSKI Z, VAIKUNTANATHAN V. Lattice-based FHE as secure as PKE[C]//The 5th Conference on Innovations in Theoretical Computer Science. 2014: 1-12.

[19] 陈智罡, 宋新霞，赵秀凤. 一个LWE上的短公钥多位全同态加密方案[J]. 计算机研究与发展, 2016,53(10): 2216-2223. CHEN Z G, SONG X X, ZHAO X F. A multi-bit fully homomorphic encryption with better key size from LWE[J]. Journal of Computer Research and Development, 2016, 53(10): 2216-2223.

[20] 陈智罡, 石亚峰, 宋新霞. 全同态加密具体安全参数分析[J]. 密码学报, 2016, 3(5): 480-491. CHEN Z G, SHI Y F, SONG X X. Estimating concert security parameters of fully homomorphic encryption[J]. Journal of Cryptologic Research, 2016, 3(5): 480-491.

[21] 陈智罡, 王箭, 宋新霞. 全同态加密研究[J]. 计算机应用与研究, 2014, 31(6): 1624-1631. CHEN Z G, WANG J, SONG X X. Survey on fully homomorphic encryption[J]. Application Research of Computer, 2014, 31(6): 1624-1631.

NTRU-type fully homomorphic encryption scheme without key switching

SONG Xin-xia1, CHEN Zhi-gang2, ZHOU Guo-min3

(1. College of Junior, Zhejiang Wanli University, Ningbo 315100, China; 2. College of Electronic and Computer, Zhejiang Wanli University, Ningbo 315100, China; 3. Department of Computer and Information Technology, Zhejiang Police College, Hangzhou 310053, China)

In order to construct a fully homomorphic encryption scheme based on NTRU cryptosystem from ring learning with errors, noise growth and homomorphic property in the NTRU cryptosystem were analyzed. The concept of zero homomorphic encryption was introdced and that the NTRU cryptosystem was zero homomorphic encryption was shown. A BGN homomorphic encryption scheme and a fully homomorphic encryption scheme were proposed based on the NTRU cryptosystem. In the proposed NTRU-type fully homomorphic encryption scheme, the secret key doesn’t change in homomorphic multiplications. Thus a fully homomorphic encryption scheme can be obtained without key switching that was used in the previous fully homomorphic encryption schemes. Moreover, the ciphertext is a vector in the proposed NTRU-type fully homomorphic encryption scheme which has the advantage of storage and transmission compared to GSW fully homomorphic encryption scheme where the ciphertext is a matrix.

fully homomorphic encryption, NTRU cryptosystem, ring learning with errors, key switching, BGN homomorphic encryption

TP309.7

A

10.11959/j.issn.2096-109x.2017.00117

宋新霞（1973-），女，陕西户县人，浙江万里学院副教授，主要研究方向为代数密码。

陈智罡（1972-），男，四川资中人，博士，浙江万里学院副教授，主要研究方向为全同态加密、格公钥密码学。

周国民（1971-），男，浙江义乌人，浙江警察学院副教授，主要研究方向为网络安全与执法。

2016-09-10；

2016-10-30。通信作者：陈智罡，zhig.chen@foxmail.com

浙江省自然科学基金资助项目（No.LYNF020002）；浙江省公益性技术应用研究计划基金资助项目（No.2017C33079）；NSFC—浙江两化融合联合基金资助项目（No.U1509219）；宁波市自然科学基金资助项目（No.2016A610226）

Foundation Items: Zhejinag Provincial Natural Science Foundation of China (No.LYNF020002), The Public Projects of Zhejiang Province (No.2017C33079), NSFC-Zhejiang Joint Fund for the Integration of Industrialization Information (No.U1509219), Ningbo Natural Science Foundation (No.2016A610226)