基于随机序列统计特性的伪随机序列生成方法

柏森，周龙福，郭辉，闫兵

（1. 重庆工程学院软件学院，重庆400056；2. 重庆通信学院信息工程系，重庆400035；3. 61541部队，北京 100094）

基于随机序列统计特性的伪随机序列生成方法

柏森1,2，周龙福1，郭辉3，闫兵2

（1. 重庆工程学院软件学院，重庆400056；2. 重庆通信学院信息工程系，重庆400035；3. 61541部队，北京 100094）

在现有生成伪随机序列的方法中，产生的伪随机序列存在均衡性、游程特性不够好的问题。根据随机序列的统计特性，在骑士巡游问题 SemiHam求解算法的基础上，提出了基于随机序列统计特性的伪随机序列生成方法。首先，对棋盘中的格子设定不同长度的0、1游程值；然后，再用骑士巡游问题SemiHam求解算法产生的Hamilton圈对设定游程值的棋盘进行扫描；最后，取出0、1游程值，得到伪随机序列。实验结果表明，该算法产生的伪随机序列满足随机序列统计特性，且随机性较好。

伪随机序列；随机序列统计特性；SemiHam算法；NIST SP800-22随机性测试

1 引言

在数据加密的应用中，人们希望得到真正的随机序列，但能否重复产生真正的随机序列，一直是争论的问题。由于伪随机序列能够重复产生和处理[1]，并且具有良好的随机特性，在数据加密[2]、卫星导航[3]、扩频通信[4]、探地雷达[5]等方面都有广泛的应用。因此，伪随机序列的生成方法一直是研究的重点问题之一。

良好的伪随机序列应具有真随机序列的统计特性[6]：伪随机序列中0和1的数量相等或相差1个；游程个数为序列长度的，长度为l的游程个数占总游程个数的。目前产生伪随机序列的方法主要有混沌[7～10]、有限域[11]、自动细胞机[12]等，但这些方法产生的伪随机序列不能完全满足真随机序列的统计特性。文献[7]给出了基于二维新混沌系统的伪随机序列生成方法，利用二维混沌系统产生混沌序列，序列通过取余得到密码流，十进制转化为二进制，得到伪随机序列。文献[10]通过Logistic混沌产生混沌序列，设定阈值量化混沌序列，产生二进制序列。文献[11]用椭圆曲线和迹函数，通过设定参数值产生伪随机序列。文献[12]提出了基于细胞自动机的组合伪随机序列的生成方法，用一组单个细胞自动机产生伪随机序列，将序列的一部分采用异或运算进行组合，将组合序列与其他序列进行异或组合，产生伪随机序列。这些方法产生的伪随机序列均衡性、游程特性较差，0、1数量相差较大，不同长度的游程个数与真随机序列的游程个数有偏差。

本文在骑士巡游问题 SemiHam求解算法随机生成Hamilton圈[13]的基础上，根据伪随机序列统计特性，提出了基于伪随机序列统计特性的伪随机序列生成方法。该方法首先对棋盘中的格子设定不同长度的0、1游程值，再用骑士巡游问题SemiHam求解算法产生的 Hamilton圈对设定游程值的棋盘进行扫描，取出0、1游程值，得到伪随机序列。

2 骑士巡游问题SemiHam求解算法

在一个棋盘中，求解骑士巡游问题的方法很多[13～16]。文献[13]中骑士巡游问题求解的SemiHam 算法是在马步图中随机找出一条Hamilton圈的方法，通过简单扩展（simple extension）、圈扩展（cycle extension）和旋转（rotation）的方法，随机产生顶点序列，算法流程如图1所示。

首先，将一个具有N格的棋盘转换为N个顶点的马步图和N×N的邻接矩阵，并将顶点标识为0～N−1。其次，随机选取一个起始点，通过simple extension的方法，依次在序列首和序列尾扩展；当序列首和尾有边连接时（形成圈），通过 cycle extension的方法对圈序列进行拆分，并继续进行简单扩展；当simple extension与cycle extension不能进行时，进行rotation操作，直到简单扩展、圈扩展和旋转操作不能进行为止。最后，检查各顶点是否遍历、序列头和序列尾是否有边连接，当遍历各顶点且序列头和序列尾有边连接时，则成功；否则，失败。

简单扩展（simple extension）。简单扩展分为序列头扩展和序列尾扩展，如果序列头的顶点可以跳动到未历经的顶点时，在序列头随机添加未历经的新顶点；如果序列尾的顶点可以跳动到未历经的顶点时，在序列尾随机添加未历经的新序列尾顶点。

圈扩展（cycle extension）。当序列v0v1…vl−1vl尾顶点与序列头顶点有边连接时，此序列为一个圈。对序列进行拆分，依次检测各顶点是否可以跳动到未历经的顶点，此顶点一定存在，若存在多个这样的顶点，则随机选取一个顶点 vi，在此处进行拆分，vivi−1…v1v0和 vlvl−1…vi+1vi，然后对序列vivi−1…v1v0vlvl−1…vi+1vi进行简单扩展。

旋转（rotation）。如果与序列头、序列尾连接的顶点都在序列中，对序列进行旋转操作。序列 v0v1…vl−1vl检查 v2～vl−1是否有顶点与 v0有边连接，当顶点vi与v0有边连接时，对v0…vi−1旋转，旋转后的序列为vi−1…v0vi…vl−1vl，对序列进行简单扩展和圈扩展；检查序列v0v1…vl−1vl的尾顶点vl，看v1v2…vl−2是否有与尾顶点vl有边连接，如果顶点 vi与 vl有边连接时，对 vi+1…vl旋转，旋转后的序列为 v0v1…vivl…vi+1，再进行简单扩展和圈扩展。

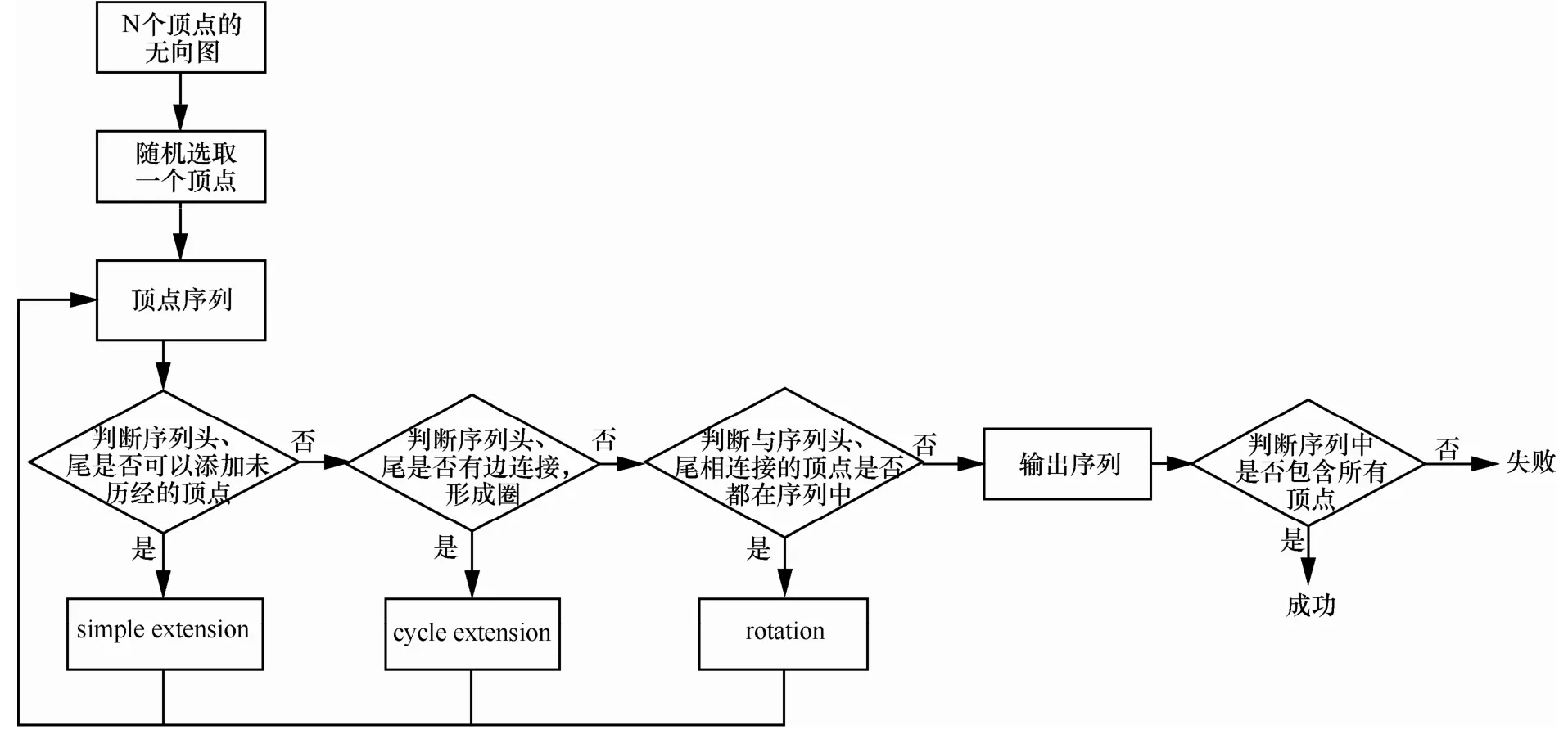
图1 骑士巡游问题SemiHam求解算法流程

3 基于骑士巡游问题解的伪随机序列生成方法

3.1 基本思想

骑士巡游问题是寻找棋盘中的一条Hamilton圈。由于马步的跳动是按照“日”的方式，行跳一个格子，列跳2个格子；或行跳2个格子，列跳1个格子。当棋盘中的格子以黑、白交叉分布时，马跳动的轨迹也是黑、白交叉的，图2为棋盘中骑士巡游轨迹的部分显示。如果一个白、黑格子分别代表一个0游程和1游程，那么，通过骑士巡游路径组合各格子的游程值，就可以得到具有 n（棋盘格子数）个游程的序列。骑士巡游问题 SemiHam求解算法是在马步图中随机生成的一条Hamilton圈，根据随机序列的统计特性，对棋盘中的格子赋不同长度的游程值，按照骑士巡游问题 SemiHam求解算法产生的骑士巡游问题路径，对棋盘中的格子进行扫描，取出游程值，产生伪随机序列。

3.2 棋盘的赋值

1) 棋盘赋值路径

图3为一个黑、白格子棋盘，其中，白格子代表0游程用0来表示；黑格子代表1游程用1来表示。一串0、1交叉的数据串对棋盘进行赋值。当采用横向扫描（光栅扫描）的方法对棋盘赋值，列数为奇数时，可以正确赋值，黑、白格子交叉即0、1交叉分布，如图3(a)所示。当列数为偶数时，棋盘则赋值不正确，0游程和1游程在同一列，如图3(b)所示，马在棋盘中跳动时，会出现连续0或1的情况。所以，不是所有的扫描方法都适合对棋盘进行赋值。经过对扫描方法的研究[17]，可以按照c、o、a、s、z、b扫描方式进行（如图4所示）。文中采用的扫描方式为c方式（如图5所示），这种方式对奇、偶数列都可以正确赋值。

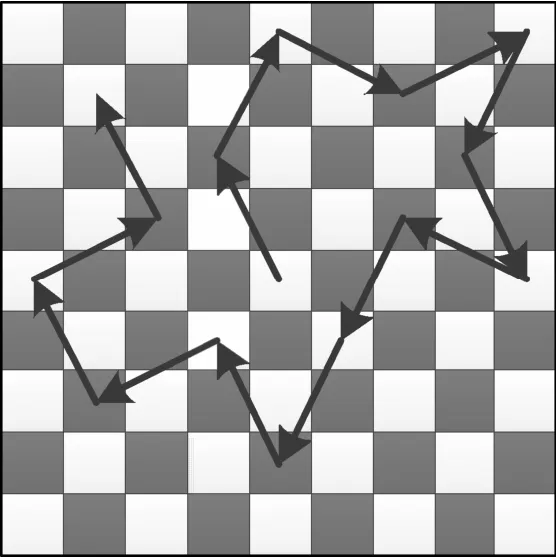
图2 骑士巡游路径的部分显示

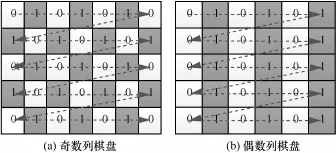
图3 光栅扫描的方式赋值

图4 扫描方式

图5 c扫描的方法赋值

2) 棋盘赋值方法

伪随机序列是具有随机特性的统计特性[6]。序列中0和1的个数接近相等；序列中长度为1的游程约占游程总数的，长度为2的游程约占总游程数的，长度为l的游程约占总游程的（如表1所示）。但在实际应用中，伪随机序列不可能完全满足游程的统计特性，在某些长度的游程上存在一点偏差。例如，一个具有25个游程的伪随机序列，长度为1的游程个数为12.5，长度为2的游程个数为6.25，长度为3的游程个数为3.125，长度为4的游程个数为1.562 5，长度为5的游程个数为0.781 25。当完全满足伪随机序列的统计特性时，游程个数可能会出现小数的情况。

表1 长度为l的游程个数占总游程比例

为了满足随机序列的统计特性，在此问题上，做如下处理。首先，确定长度为l的游程数，统计特性求出的游程个数除以 2，得到的值通过四舍五入，得出长度为l的0游程的个数或1游程的个数。其次，确定游程总数，当游程总数为偶数时，0游程和1游程各为游程总数的；当游程总数为奇数时，0游程比1游程多1个，多的1个游程值设为0，在求出的长度为1的0游程数上加 1即可。通过设定，上面的例子得到很好的解决，长度为1的游程个数为13，0游程的个数为7，1游程的个数为 6；长度为 2的游程为 6，0游程和1游程的个数分别为3；长度为3的游程个数为4，0游程和1游程的个数分别为2；长度为4的游程个数为2，0游程和1游程的个数分别为1；各游程数相加，得到总的游程个数为25。通过以上的设定，0、1的数量相等或多一个0，不同长度的游程数满足统计特性。

根据统计特性中游程的个数及不同游程所占比例，对棋盘进行赋值。长度为1的游程，首先设置长度为1的0游程，从第一个白格子开始设置，每隔3个格子设置0；长度为1的1游程，在长度为1的0游程后面一个格子赋值1即可。长度为l的0游程，从第一格开始扫描，第一格未赋值的点设置l个0，每隔2l+1–1个格子设置l个0，长度为l的1游程，在长度为l的0游程后一格添加即可。

3.3 伪随机序列生成方法的步骤

伪随机序列生成方法的步骤如下。

Step1 生成一个m×n的赋值棋盘。

设置棋盘的大小，即棋盘的行数m和列数n。计算不同长度的游程个数，创建一个空数组Q，并按照3.2节的方法为Q赋值，Q中的各值为游程的长度。按照c扫描的方式得到m×n的赋值棋盘。

Step2 利用骑士巡游问题SemiHam求解算法生成与棋盘大小相等的顶点序列，转化为骑士巡游路径。

骑士巡游问题SemiHam求解算法产生的是被标识的顶点序列，利用式(1)和式(2)求出马步图中的骑士每步所在的位置，得到骑士巡游路径。

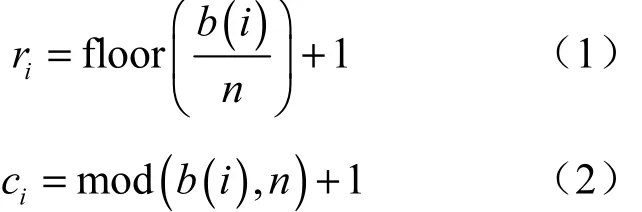
Step3 按照骑士巡游路径的方式，扫描赋值棋盘，得到伪随机序列。

伪随机序列的生成原理如图6所示。

算法举例：对一个5×6的棋盘进行赋值（如图7(a)所示），利用骑士巡游问题SemiHam求解算法产生的5×6骑士巡游路径（如图7(b)所示），骑士巡游路径对相同大小的赋值棋盘进行扫描，得到伪随机序列。例如，一个骑士巡游路径0、8、4、17、28、15、23、27、19、6、2、10、21、29、16、5、9、1、12、25、14、18、26、22、11、3、7、20、24、13。根据序列路线扫描棋盘赋值图，得到伪随机序列为01010111100110001100111010 10101000011100110001100101。

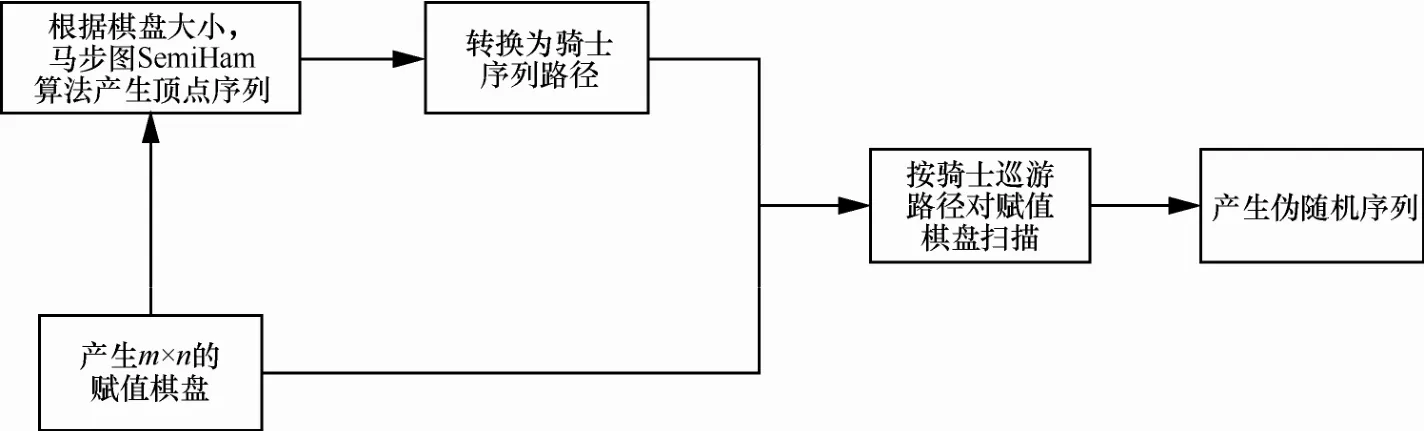
图6 伪随机序列生成原理

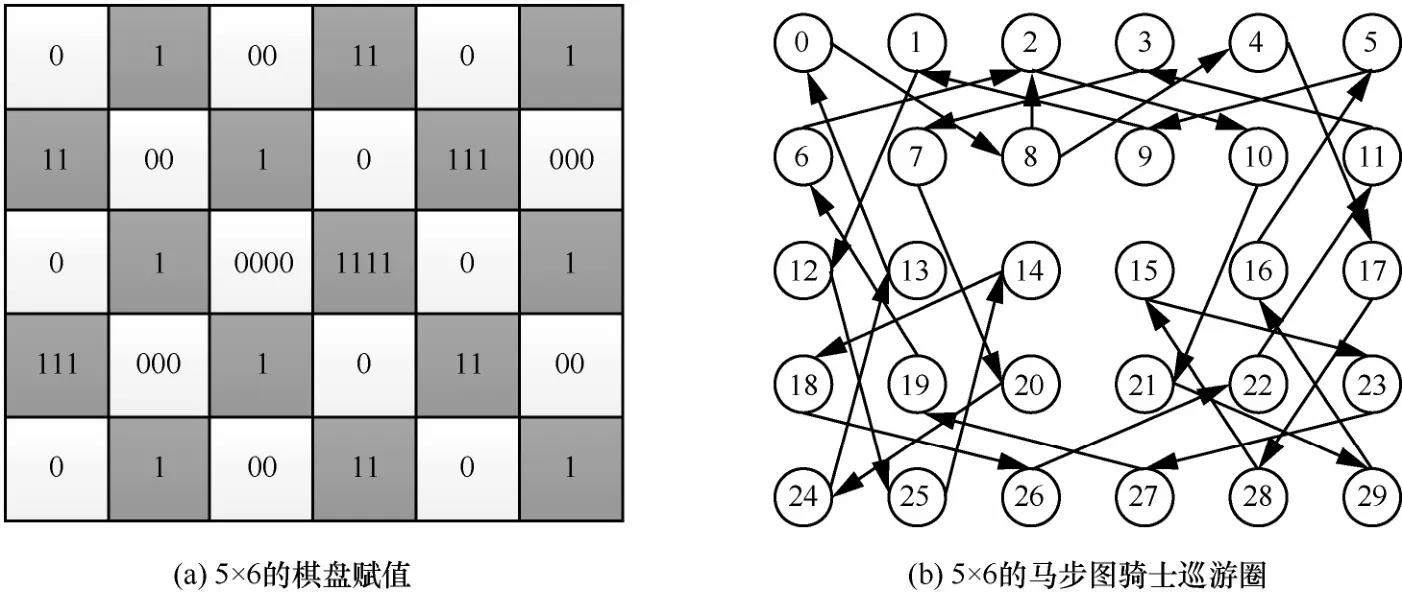
图7 5×6的棋盘赋值及骑士巡游圈

4 实验结果及分析

4.1 实验结果

本文算法是在伪随机序列统计特性的基础上，产生赋值棋盘，并通过骑士巡游路径产生伪随机序列。所以，伪随机序列中0、1的个数和不同长度游程的个数取决于棋盘中的赋值。当棋盘中的格子数为偶数时，0、1的数量相等；当棋盘中的格子数为奇数时，0的数量比1的数量多1个。如表2所示，伪随机序列的0、1的个数相等或相差一个，序列的均衡性较好。

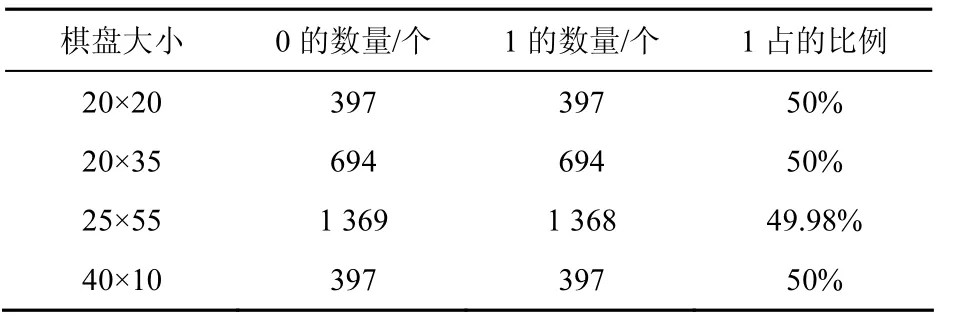
表2 伪随机序列中0、1的数量

一个伪随机序列在理想的情况下，长度为 l的游程占总游程的。由本文算法产生伪随机序列的统计情况如表3所示，长度为l（l 〉1）的游程中游程数为偶数，这是为保持序列的均衡性即0、1的数量相等，设定不同长度的0游程和1游程的个数相等。另一个原因，在计算游程个数时，并不是所有的游程个数结果为整数，可能会出现小数部分，所以游程个数并不是完全符合理想的情况。本文算法产生的伪随机序列符合随机序列的游程特性。

4.2 随机性分析

本文算法产生的伪随机序列进行了随机性测试，测试软件为美国国家标准与技术研究所的NIST SP800-22测试包，sts-2.1.1测试软件[18]。测试软件测试项目为15项，由于每一项测试对序列的长度有要求，只进行了其中的部分项目测试。当测试值≥ 0.01时，认为序列在该项测试中为随机的；当测试值＜ 0.01时，认为序列在该项的测试中为非随机的。本文算法在20×35的赋值棋盘上产生 5组伪随机序列，用sts-2.1.1测试软件对产生的伪随机序列进行测试，测试结果如表4所示。

由测试结果可以看出，只有一个测试项未通过测试，大多数测试值较大，本算法产生的伪随机序列的随机性较好。Frequency Test测试值为1，表示伪随机序列中0和1的个数相等，序列的均衡性较好。Frequency Test within a Block测试值中4个在0.7以上，其中2个在0.9以上，说明子块中1的分布与0的分布较为接近。Runs Test测试值相等，表示各序列中的游程个数相等，测试值为0.747 379，说明序列中游程数接近真随机序列中游程的个数。Test for the Longest of Ones in a Block测试值3个值大于0.8，说明子块中最长游程的比例接近真随机分布。Serial Test测试值 3个都在0.7以上，说明指定长度的子序列出现的次数趋于等概。Cumulative Sums Test测试值4个值都在0.7以上，说明0、1的分布较为均匀。Linear Complexity Test测试值为0.000 039小于0.01，说明产生序列的线性移位器较小，序列未达到随机序列的程度。

表3 伪随机序列中不同长度的游程个数

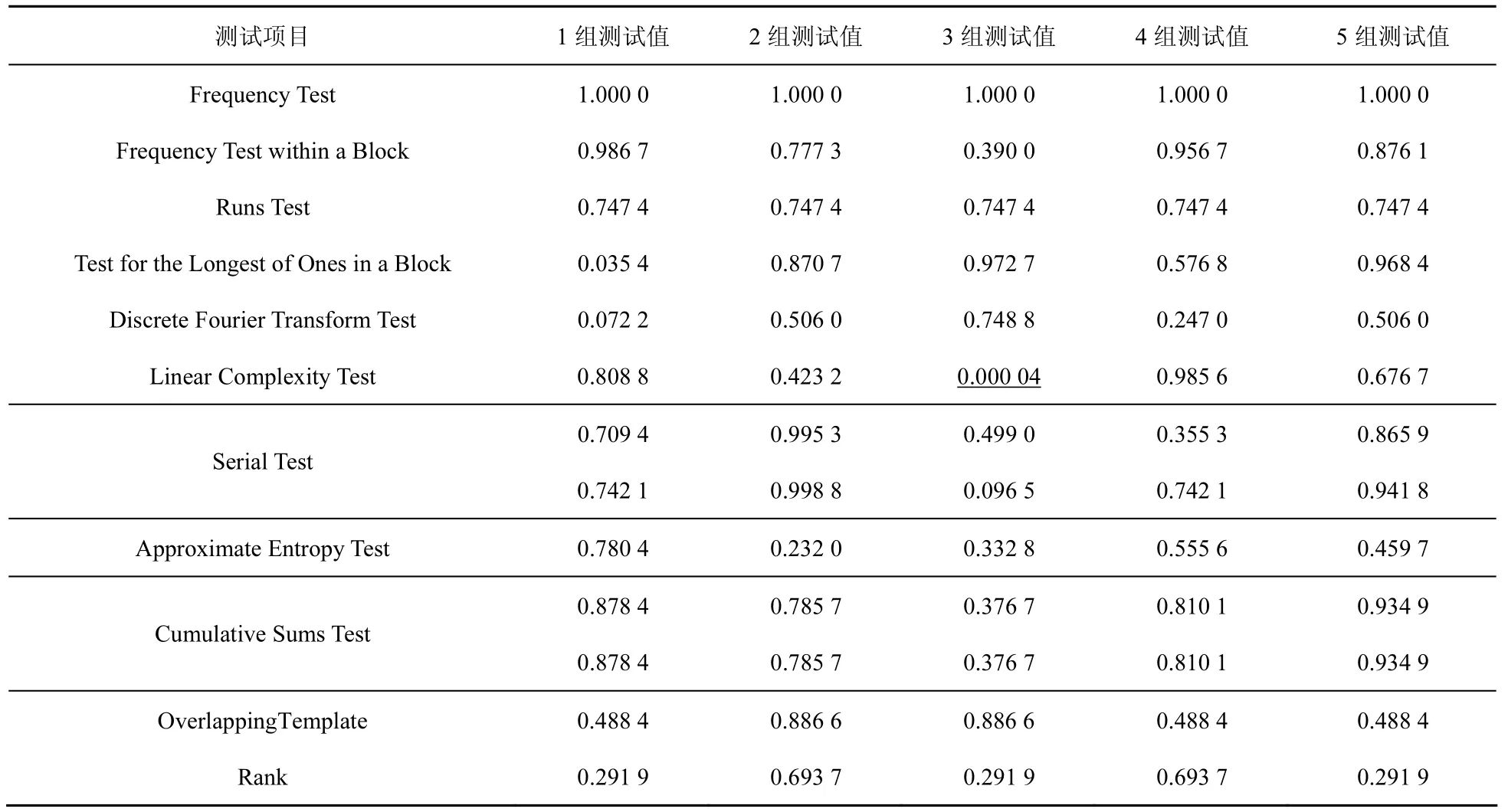
表4 随机性测试

4.3 随机性比较

文献[7,8]和文献[10]是目前较新的伪随机序列生成方法，但文献[7]使用FIPS 140-2进行随机性测试，不便与本文进行比较。文献[8]使用硬件FPGA产生伪随机序列，不好用来与本文算法进行比较。因此，选择与文献[10]算法进行随机性比较，分别产生5组长度约为1 400的伪随机序列。根据NIST SP800-22测试标准[18]，利用sts-2.1.1测试软件进行测试。测试结果如表5所示，测试值为每种算法5组伪随机序列的平均值。

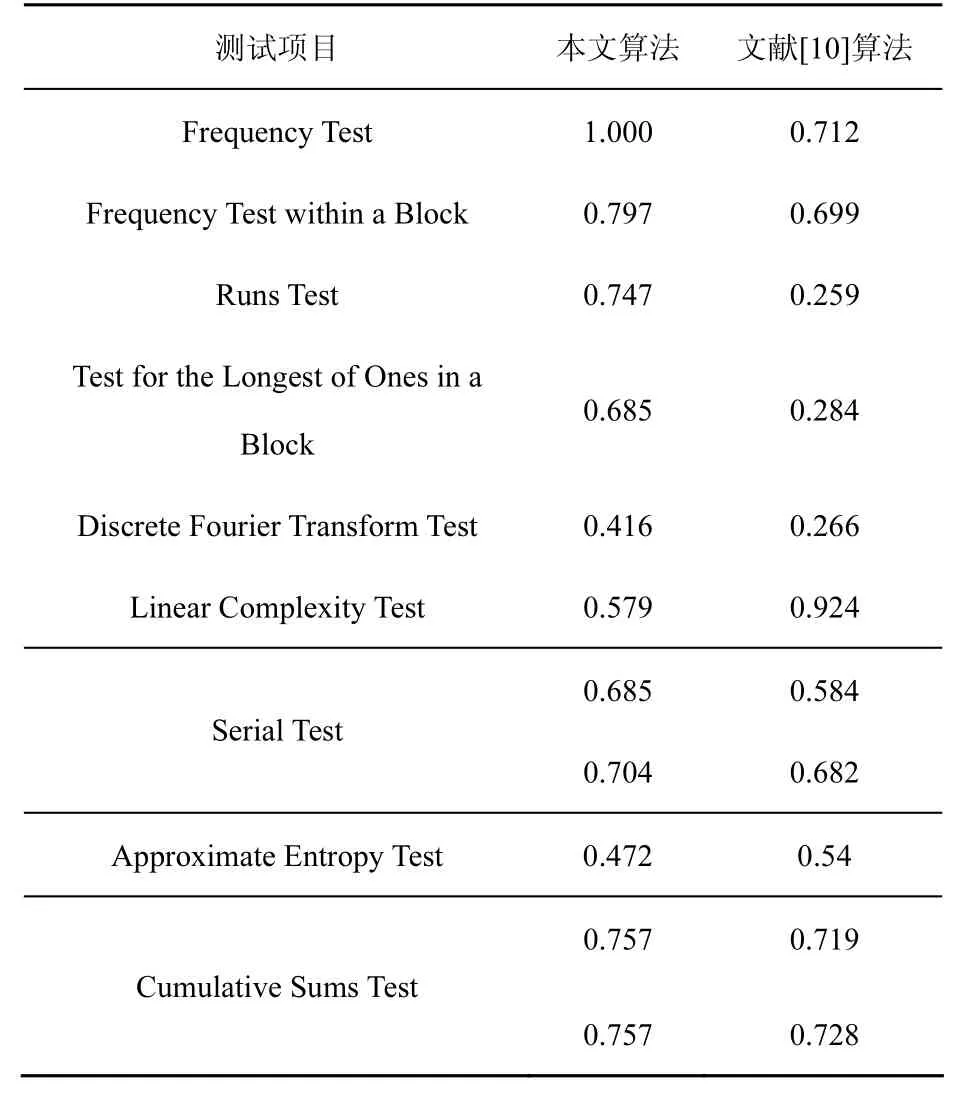
表5 随机性比较

由表5可以看出，在9项测试中，本文算法有8项测试值大于文献[10]算法。本文算法在线性复杂度上小于文献[10]算法，说明序列复杂度相对较低，但测试值都在0.5以上，满足随机性要求。从总体随机性上看，本文算法好于文献[10]算法。

5 结束语

本文基于骑士巡游问题的SemiHam求解算法，设计了伪随机序列生成方法。实验结果的对比分析表明，设计算法产生的伪随机序列满足随机序列统计特性，有较好的均衡性和游程特性，且随机性较好。当棋盘较大时，棋盘的赋值运算较少，运行效率高，但骑士巡游问题SemiHam求解算法求骑士巡游路径较复杂，运行效率低。下一步将研究大棋盘的分块，用骑士巡游问题 SemiHam求解算法产生多条骑士巡游路径对各分块进行扫描，组合各块序列，得到更大长度的伪随机序列。

[1] 吴资玉, 韩庆文, 通信原理[M]. 北京: 电子工业出版社, 2008: 316-317. WU Z Y, HAN Q W. Principles of communications[M]. Beijing: Publishing House of Electronics Industry. 2008: 316-317.

[2] HUANG X, YE G. An image encryption algorithm based on hyper-chaos and DNA sequence[J]. Multimedia Tools and Applications, 2014, 72(1): 57-70.

[3] 雷雄俊, 刘光斌. GPS伪随机序列的构成及应用分析[J]. 光通信研究, 2010, 21(6): 64-67. LEI H J, LIU G B. Architecture and applications of GPS pseudo-random sequence[J]. Study on Optical Communications, 2010, 21(6): 64-67.

[4] AHMED Z, CANCES J P, MEGHDADI V. Cryptographic spread spectrum relay communication[C]//Next Generation Mobile Applications, Services and Technologies. 2008: 588-591.

[5] 张群英, 方广有. 伪随机序列编码脉冲信号在探地雷达中的应用研究[J]. 电子与信息学报, 2012, 33(2): 424-428. ZHANG Q Y, FANG G Y. The study of pseudo random sequence’s application to GPR[J]. Journal of Electronics & Information Technology, 2012, 33(2): 424-428

[6] 杜小妮. 伪随机序列的构造及其随机性分析[D]. 陕西: 西安电子科技大学, 2008. DU X N. The construction and randomness analysis of pseudo random sequence[D]. Shaanxi: Xidian University, 2008.

[7] 张丽姣, 闵乐泉, 韩双霜. 二维新混沌系统和伪随机数生成器的设计[J]. 计算机工程与设计, 2014, 35(4): 1178-1182. ZHANG L J, MIN L Q, HAN S S. Design of 2-dimensional novel chaotic system and pseudo-random number generator[J]. Computer Engineering and Design, 2014, 35(4): 1178-1182.

[8] 孙克辉, 叶正伟, 贺少波. 混沌伪随机序列发生器的FPGA设计与实现[J]. 计算机应用与软件, 2014, 6(12): 3-7. SUN K H, YE Z W, HE S B. Design and implementation of chaotic pseudo-random sequence generator using FPGA[J]. Computer Applications and Software, 2014, 6(12): 3-7.

[9] 李家标, 曾以成, 陈仕必, 等. 改进型Henon映射生成混沌伪随机序列及性能分析[J]. 物理学报, 2011, 60(6): 126-130. LI J B, ZENG Y C, CHEN S B. Modified Hénon map generated chaotic pseudorandom-bit sequences and performance analysis[J]. Acta Physica Sinica, 2011, 60(6): 126-130.

[10] 叶珍, 臧鸿雁. 基于混沌系统的量化方法及伪随机性研究[J].计算机应用研究, 2014, 31(12): 3719-3721. YE Z, ZANG H Y. Research of quantization methods and pseudorandomness based on chaotic systems[J]. Application Research of Computers, 2014, 31(12): 3719-3721.

[11] 花文昭, 韩文报. 基于椭圆曲线的二元伪随机序列构造与分析[J]. 计算机工程, 2012, 38(18): 100-102. HUA W Z, HAN W B. Construction and analysis of binary pseudorandom sequences based on elliptic curve[J]. Computer Engineering, 38(18): 100-102.

[12] JESSA M, JAWORSKI M. Producing secure pseudorandom sequences with combined multiplicative congruential generators[C]// Systems, Signals and Image Processing (IWSSIP).2012: 160-163.

[13] NIVASCH G. Experimental results on hamiltonian-cycle-finding algorithms[R]. Weizman Institute, Israel, 2003.

[14] 柏森, 杨晓帆. 求马步图 Hamilton 圈的最优算法[J]. 计算机工程与科学, 2000, 22(2): 8-11. BAI S, YANG X F. An optimal algorithm for searching a Hamilton cycle of the knight-tour’s problem[J]. Computer Engineering & Science, 2000, 22(2): 8-11.

[15] DEMAIO J. Which chessboards have a closed knight's tour within the cube[J]. Journal of Combinatorics, 2007, 14(2): 1-9.

[16] BAI S, LIAO X F, QU X H, et al. Generalized knight's tour problem and its solutions algorithm[C]//2006 International Conference on Computational Intelligence and Security. 2006:570-573.

[17] SIVAKUMAR T, VENKATESAN R. A novel approach for image encryption using dynamic scan pattern[J]. IAENG International Journal of Computer Science, 2014, 41(2): 91-101.

[18] RUKHIN A, SOTO J, NECHVATAL J, et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications[R]. Booz-Allen and Hamilton Inc Mclean Va,2001.

Method to generate the pseudo random sequence based on the statistical properties

BAI Sen1,2, ZHOU Long-fu1, GUO Hui3, YAN Bing2
(1. School of Software, Chongqing Institute of Engineering, Chongqing 400056, China; 2. Information Engineering Department, Chongqing Communication Institute, Chongqing 400035, China; 3. Unit 61541 of PLA, Beijing 100094, China)

There are some problems existing in pseudo-random sequence generating methods, such as the weaker proportionality, bad run length characteristic, etc. Hence, based on the SimiHam algorithm in Knight’s tour problem, a pseudo-random sequences generating method was proposed according to the statistical properties of random sequence. First, set runs value 0 and 1 in different length for the grids in chessboard, and then scan the chessboard with Hamilton cycles which are generated by SemiHam algorithm in Knight’s tour problem, At last extract run length values of 0 and 1 and get the pseudo-random sequences. Experimental results show that the pseudo-random sequence generated by the proposed algorithm satisfies the statistical properties of a random sequence and has better randomness.

pseudo-random sequence, statistical properties of a random sequence, SemiHam algorithm, NIST SP800-22 random test

TN919.81

A

10.11 959/j.issn.2096-109x.2017.00125

柏森（1963-），男，四川达县人，博士，重庆工程学院教授、硕士生导师，主要研究方向为信息隐藏、图像加密。

周龙福（1971-），男，江西临川人，硕士，重庆工程学院副教授，主要研究方向为软件体系结构、数据库、网络与系统安全。

郭辉（1982-），男，河南辉县人，硕士，61541部队工程师，主要研究方向信息安全。

闫兵（1993-），男，湖南常德人，重庆通信学院硕士生，主要研究方向信息安全。

2016-10-24；

2016-12-02。通信作者：柏森，baisecq@126.com

国家自然科学基金资助项目（No.61272043）；重庆市基础与前沿研究计划基金资助项目（No.cstc2013jjB40009）；应急通信重庆市重点实验室能力提升基金资助项目（No.cstc2014pt-sy40003）

Foundation Items: The National Natural Science Foundation of China(No.61272043)，Basic & Frontier Project of Chongqing (No.cstc2013jjB40009), Capability Enhancement Foundation of Chongqing Key Laboratory of Emergency Communication (No.cstc2014pt-sy40003)