合作网络高阶聚集特性研究

杨忠明，梁本来，秦 勇，卢庆武

(1.广东科学技术职业学院 计算机工程技术学院，广东 珠海 519090; 2.中山职业技术学院 信息工程学院，广东 中山 528404; 3.东莞理工大学 计算机学院，广东 东莞 523808; 4.惠州学院 教育技术中心，广东 惠州 516007)

合作网络高阶聚集特性研究

杨忠明1，梁本来2，秦 勇3，卢庆武4

(1.广东科学技术职业学院 计算机工程技术学院，广东 珠海 519090; 2.中山职业技术学院 信息工程学院，广东 中山 528404; 3.东莞理工大学 计算机学院，广东 东莞 523808; 4.惠州学院 教育技术中心，广东 惠州 516007)

情报学领域的研究表明,研究工作者形成的科研合作关系网络是一个非连通网络,但是网络统计参数呈现出无尺度网络特性和小世界网络特性,合作网络是一种描述科研合作的典型网络。提出高阶聚集系数的概念，以期刊作者的合作网络数据为计算案例，计算期刊合作者的高阶聚集系数C(h)，形成图表并分析其高阶聚集系数C(h)在图中所表示的意义。通过采集国内计算机类一级学报的大量合作者样本数据并通过计算分析表明，合作者为20人左右时，合作团队拥有广泛的知识面和较高的合作水平，较易做出高水平的创新性成果，也意味着高水平的论文作者通常和学者20人左右直接或者间接保持合作关系。高阶聚集系数同样可用于语言网络等其他呈现出小世界效应的网络分析。

合作网络；小世界网络；高阶聚集系数；平均距离

1 概 述

网络可以用来描述人与人之间的社会关系、计算机之间的网络联接、网页之间的超链接、科研文章之间的引用关系等，而统计物理学是从微观到宏观的桥梁。研究网络中顶点与边的度值与权值等微观性质与网络的几何性质、效率与稳定性等宏观性质之间的关系正是复杂网络研究的核心内容。因而，与图论的研究有所不同，复杂网络的研究更侧重于从各种实际网络的现象之上抽象出一般的网络几何量，并用这些一般性质指导更多实际网络的研究，进而通过讨论实际网络上的具体现象发展网络上模型的一般方法，最后讨论网络本身的形成机制。在模型研究、演化机制与结构稳定性方面的丰富研究经验是在复杂网络研究领域得到广泛应用的原因；而图论与社会网络提供的网络静态几何量及其分析方法是复杂网络研究的基础，并得到了充分发展。合作网络属于复杂网络中社会网络的一种，它的提出是复杂网络系统研究的一个新的方向[1]。小世界网络中利用聚集度的计算来评价网络指标、反映网络性质的合作网络已成为评价网络指标的一种重要评价方法。根据权威文献表明，合作网络是一种优化评价网络指标的评价系统，自1993年到2010年，持续多年的研究更表明了合作网络的评价优化。科学合作的范围随着科学的进步而逐渐增长。论文合著是科学合作的表现之一，随着不同领域的合作者的介入，科学合作成果的质量也越来越好，合作网络成为更复杂的网络。

一个典型网络是由许多节点与连接两个节点间的一些边组成的，而复杂网络简单来说是呈现高度复杂性的网络，具有结构复杂、网络进化、连接多样性、动力学复杂性、节点多样性和多种复杂性融合的特点。复杂网络是具有自组织、自相似、吸引子、小世界、无标度网络中部分或全部性质的网络。合作网络是描述合作关系的网络，它属于复杂网络中社会网络的一种。

两个现实的复杂网络模型被广泛应用：小世界模型和无尺度模型。文中重点讨论小世界网络，其特征是局部集群连接的长的线，平均距离之间的顶点的对数的增长与网络中N的大小有关。以日常语言看，它反映的是相互关系的数目可以很小但却能够连接世界的事实，且小世界模型社会网络就是小世界的一种。科研人员合作网络是描述科研人员合作关系的网络，通常把每个科研人员作为网络中的一个顶点(或称节点)，如果两个科研人员之间共同发表过一篇论文，这两个顶点之间就连接一条边。科研人员之间形成了一个复杂网络，该网络的节点的复杂性、网络演化特性以及网络的合作行为等问题，所呈现出的密集度可以作为评价期刊的一个指标。研究基于合作网络的期刊高阶聚集特性分析，通过其看聚集度的计算发现目前研究热点，同时聚集度越大，合作越紧密，可作为评价期刊的一个重要指标。

Watts和Strogatz[2]构造出一种介于规则网络和随机网络之间的网络(WS网络)。随后Newman和Watts[3]给出一种新的网络构造方法。在NW网络中，原有的连边并不会被破坏，而是以一个很小的概率在原来的规则网络上添加新的连边，这样构造出的网络也同时具有大的簇系数和小的平均距离。BarabasiA[4]对科学合作社会网络的演化进行研究，认为作者合作社会网络是复杂网络的代表。

Watts和Strogatz的研究方法是通过其中一个规则网络转化为小世界网络，这种方法很少或基本没有改变顶点度的分布和量化参数。小世界网络中一个重要特征就是与随机网络相比有相当高的聚集系数，甚至比任意网络的都要高。聚集系数的定义如下。顶点v在图G中有相邻节点度k(v)，k(v)的相邻节点可能被连接成k(v)(l(v)-1)/2条边。实际存在的最大可能的边的分数数量就是图G的聚集系数Cv，所有节点v的平均聚集系数就是网络G的聚集度C。C的值接近于1意味着网络是高连通的。

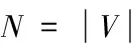
国内外学者在合作网络的构造、静态统计性质分析和演化模型等方面进行了研究。2006年Cardillo等分析了LosAlamos的2000-2005年间cond-mat数据库，发现该库的成长是通过合作网络图的连接增长体现的，主要特征体现在度-度相关性以及节点的聚集相关性[7]。周涛等提出了基于二分图资源的推荐算法[8]。李晓佳等[9]在自建的合作网络上，实现了层次聚集法和介数聚集法，在Newman的Q函数基础上讨论了聚集过程中的最佳集团数。还有学者从不同角度对社团网络及其应用做了研究，如范超等[10]利用合作网络及社会网络的结构知识对CNM算法作了改进，提高了社团发现的精度。

黄开木等[11]以近30年国内“竞争情报”领域作者合著发表期刊论文为研究对象，分析表明该领域科学家的产量、最大合著群体的产量和所有合著群体的规模都满足幂律分布。通过对该合著网络最大连通子图的统计分析，发现该合著群体具有高聚类和小世界性。

文中采集国内计算机领域一级学报的大量合作者样本数据，分析期刊作者的合作网络数据，计算其高阶聚集特性，分析期刊的作者合作情况，把高阶聚集系数的实验结果作为评价和衡量期刊作者合作的重要指标。通过采集样本期刊的合作者数据，计算合作者的高阶聚集系数，分析期刊合作者情况，考虑以高阶聚集系数作为评价期刊优劣的指标之一。

文中提出的合作网络高阶聚集特征还可用于其他呈现出小世界效应的网络分析。在复杂网络的研究中，语言网络作为一个新的研究方向[12]，大都符合WS小世界模型，大多数节点只需经过少量的边便可到达。在聚集系数上，与随机语言网络相比，真实语言网络的聚集系数较高。Minett等基于词典资源，根据汉语词汇中的共字关系构建了汉字网络[13]，由汉字构建的网络表现出明显的高聚集系数和无尺度特征。刘海涛对中文、英文等15种语言的依存句法网络进行聚类研究[14]，得出这15种语言网络均是小世界网络，但聚集系数存在显著差异，通过选择网络7组特征，对15种语言进行聚类，发现英语和汉语网络整体上较接近。

2 合作网络高阶聚集特征描述

2.1 聚集系数及其含义

定义一个网络或图表G=(V,E)，设V有N个顶点或节点，E有M个边或线段，每条边定义为一对顶点(有序配对的有向图)。让一个顶点v有相邻节点k(v)，k(v)的相邻节点可能被连接成k(v)(l(v)-1)/2条边。分数最大的边事实上存在于相邻的v和聚集系数Cv之间，平均聚集系数对所有v∈V是那个聚集系数C的网络G。一个网络C接近1可能包括聚集和有高度的连接，或稀疏的连接在本地群集中。

2.2 高阶聚集系数的定义

文中延伸Watts和Strogatz的聚集系数，定义h是相邻顶点v与顶点G的距离。假设v有邻节点h和kh(v)，k1(v)与k(v)的定义见2.1。然后最多可以有kh(v)(kh(v)-1)/2条边连接h的邻节点v。这个分数Cv(h)允许的边真实存在于h邻节点v与聚集系数h之间。假设当kh(v)=1时Cv(h)=1，这也涵盖了h=0时的特例。平均Cv(h)对所有v∈G，考虑高阶聚集系数的概念，聚集系数为h时为C(h)。聚集系数为1时C(1)是聚集系数定义在2.1的C。

顶点为N的网络有M条边，可得公式P(0)=1/N，P(1)=2M/N2>1/N。在h=1以外，不能精确地表达该值为P(h)，除了以几个固定网络为例。很多网络(小世界或反之)，P(h)的值与h一起上升直到最大值，然后下降至距离h与网络直径D越来越接近。

对于高阶聚集系数，这一趋势开始于聚集度减少，从C(0)=1到C(1)=C，然后是进一步减少。由于事实上h在增加，qh的节点数目按一定距离h的节点在增加，这些节点属于几个派系；因此，它们之间存在很多边是不可能的。在h向D靠拢的过程中，会出现不同的效果。一个极端的例子是其中每个节点在网络中到距离D的唯一节点(这有一个截然相反的单节点)，导致C(D)=1。同样的情况，C(D-1)可能广泛应用于鉴别存在多个直径和相同的相对的顶点。应注意前面的意思是在h向D靠拢的过程中C(h)会变大，并非C(h)一定要大。

因为P(h)(上升然后下降)和C(h)(下降然后上升)的趋势是相反的，所以P(h)C(h)应有一个上限值。因为一个常数c经常接近1但很少超过1，得出：

P(h)C(h)≤clogN/N

(1)

在这特例中h=1，方程(1)意味着P(1)C(1)≈logN/N。从小世界网络中知道P(1)=2M/N2≈logN/N。对于该类网络符合C(1)=C。

目前最有效的补充证据在方程(1)，利用这个确定性的小世界网络提出这个模型。事实上，通过这个模型，可以发现这种趋势表现在方程(1)。反观确定性模型，这是基于Cayley的图，提供了模型所需的支撑信息，从而可得该模型的聚集系数：

(2)

模型中，t=log2N和a=(2l-1)/t是自由调整参数，关系到互连密度，从而影响了C的价值。注意那个非常广泛的网络(N,t∞)，当a是常数时C趋向a2/(a+1)2。适当选择a，能获得不同的聚集系数，同时保持一个小的顶点使at+t-1=(a+1)log2N-1。

不像现实网络中计算C(h)非常困难，文中提出的确定性模型服从数学分析，能用封闭形式表达一个高阶聚集系数。在这个确定性模型中，对于数字m相邻的顶点之间，在相邻顶点h的任何顶点给出表达式：

(3)

数字kh(v)的相邻顶点h的顶点v是有界的：

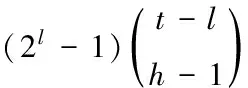
(4)

鉴于高阶聚集系数C(h)与m/(kh(v))2成正比，很容易得到高阶聚集系数为：

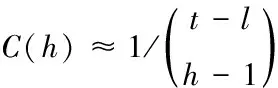
(5)

因此，定义聚集系数是基于相邻的节点，高阶聚集系数定义了涉及到一个更广泛的相邻距离参数h。利用实际上更广泛的复杂网络的实验数据，依据文中提出的确定性小世界网络模型，将网络中有关C(h)和P(h)的距离分布，定义为有一定概率的随机选择的距离为h的一对顶点。

高阶聚集系数是聚集系数的高度概括，并受聚集系统相关公式所控制。通过利用期刊作者所构成的网络数据进行实验和分析证明，不等式P(h)C(h)≤clogN/N在小世界网络中成立。这一结果明显表明该乘积P(h)C(h)有一个上限值，该上限值小于P(h)和C(h)的最大值。

高阶聚集系数的计算可以应用在期刊合作者上。把期刊合作者的数据进行高阶聚集系数C(h)的计算，可以得出一组关于顶点距离、阶数、高阶聚集系数C(h)和Cd*Pd等的数据。通过实验把数据制作成图表进行分析。期刊合作者的高阶聚集系数能得出一组曲线图，而这组曲线图的高峰能表明这时合作者人数在期刊中的普遍性，以及此时的合作者人数能做出较好的科研成果。也可以根据曲线图的高峰段来判断合作者的作品情况，可作为期刊的评价方法之一。

3 实 验

文中主要延伸Watts和Strogatz的聚集系数，计算期刊合作者的高阶聚集系数C(h)，形成图表并分析高阶聚集系数C(h)所表示的意义。

通过中国期刊网采集了《计算机研究与发展》(2000-2010)2 610篇论文共2 764位作者数据、《计算机学报》(2000-2010)2 109篇论文共1 647位作者数据和《软件学报》(2000-2010)2 602篇论文共2 462位作者数据。通过分类整理，分别把《计算机研究与发展》、《计算机学报》和《软件学报》三大期刊的作者分别输出，排列整理成文本数据，利用这些数据并通过延伸Watts和Strogatz的聚集系数，形成高阶聚集系数C(h)以计算期刊合作者的高阶聚集系数。高阶聚集系数能反映出期刊作者在不同阶段的聚集度。通过高阶聚集系数的计算与分析，能从结果中判断出期刊作者的密集性。通过输出的结果把三大期刊三组数据分别进行计算并作图，再进行比较。

3.1 高阶聚集系数的计算方法与环境

2.3节推导了高阶聚集系数的过程，利用此方法设计程序进行高阶聚集系数的计算。对实验数据首先计算最大连通子图，计算出顶点数与平均距离，继而计算各距离的点对数。根据平均距离数计算聚集度。

文中从中国期刊网将《计算机研究与发展》、《计算机学报》和《软件学报》(2000-2010)的作者信息进行数据采集，分别整理成3个单独存放作者信息的文档，再把论文是两位以上的作者进行分离和融合，形成每行为两位作者名称的格式。然后利用高阶聚集系数计算程序对3大期刊的作者数据进行计算。最后把数据信息分别整理成图表。

3.2 实验结果

计算结果如图1所示。

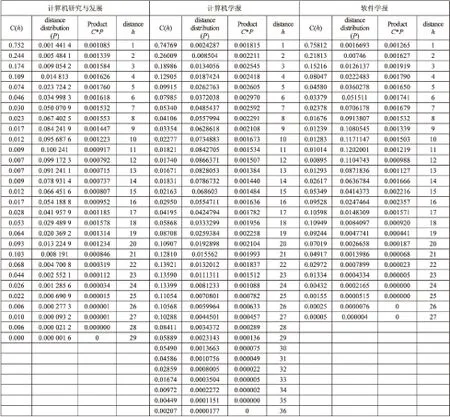
图1 高阶聚集系数计算结果

计算得出的图呈现驼峰分布型，即会出现2次高峰，在3-5的作者点集中均出现1次高峰，在后期点集中会出现2次高峰。此2次高峰将会说明作者合作群的合作关系是比较容易做出高水平创新研究成果的。三大期刊的合作者数据构成了合作网络，图2显示了三大期刊高阶聚集系数的分布情况：点集表示期刊合作者的高阶聚集系数。

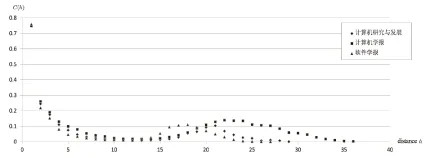
图2 三大期刊高阶聚集系数分布情况

3.3 实验分析与讨论

从图2中可以看出，图中出现了两个高峰。在合作者为2～3人的平均距离实验结果中出现第一高峰，即2～3人的合作情况比较普遍。随着合作者数量增加高阶聚集系数减小，但是合作者20人左右时出现第二聚集系数高峰。此高峰表明合作者20人左右时，合作团队拥有广泛的知识面和较高的合作水平，较易做出高水平的创新性成果，也意味着高水平的论文作者通常和学者20人左右直接或者间接保持合作关系。可以看出，这三组数据的第二高峰都处于相似的阶段，证明了高水平的论文作者和学者20人左右直接或间接保持合作关系。

4 结束语

文者提出的高阶聚集系数是聚集系数的高度概括，并受聚集系数相关公式所控制。通过利用期刊作者所构成的网络数据进行了实验分析，表明高阶聚集系数提供了对小世界网络结构的新见解，为小世界网络的探索提供了一个新的渠道。

通过实验数据结果可以看出，高阶聚集系数越高，期刊合作者合作关系越紧密，越能做出有水平的研究成果。2～3人的合作网络比较普遍，但并不意味着2～3人的合作者模式容易做出高水平成果。通过第二聚集系数高峰进行分析更具说服力，在合作者规模为20左右的合作关系比较容易做出高水平创新研究成果。文中所提出的高阶聚集系数还可应用于语言网络等其他呈现小世界效应的网络分析。

[1] 高 霞,陈凯华.合作创新网络结构演化特征的复杂网络分析[J].科研管理,2015,36(6):28-36.

[2] Watts D J,Strogatz S H.Collective dynamics of small word networks[J].Nature,1998,393(6684):440-442.

[3] Newman M E J,Watts D J.Scaling and percolation in the small-world network model[J].Physical Review E,1999,60:7332-7342.

[4] Barabasi A,Jeong H,Neda Z,et al.Evolution of the social network of scientific collaborations[J].Physical A,2002,311(3-4):590-614.

[5] Xiao Wenjun,Parhami B.Cayley graphs as models of deterministic small-world networks[J].Information Processing Letters,2006,97(3):115-117.

[6] 吴金闪,狄增如.从统计物理学看复杂网络研究[J].物理学进展,2004,24(1):18-46.

[7] Cardillo A,Scellato S,Latora V.A topological analysis of scientific coauthorship networks[J].Physica A Statistical Mechanics & Its Applications,2006,372(2):333-339.

[8] Zhou Tao,Red J,Medo M,et al.Bipartite network projection and personal recommendation[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2007,76(2):70-80.

[9] 李晓佳,张 鹏,狄增如,等.复杂网络中的社团结构[J].复杂系统与复杂性科学,2008,5(3):19-42.

[10] 范 超,王厚峰.社交网络中的社团结构挖掘[J].中文信息学报,2014,28(1):56-63.

[11] 黄开木,樊振佳,卢胜军,等.我国竞争情报领域期刊论文合著网络研究[J].情报杂志,2015,34(2):142-147.

[12] 韩 普,王东波,路高飞,等.语言网络研究进展[J].中文信息学报,2014,28(1):9-18.

[13] Minett J W,Peng G,Wang W S.The networks of syllables and characters in Chinese[J].Journal of Quantitative Linguistics,2008,15(3):243-255.

[14] 刘海涛.语言复杂网络的聚类研究[J].科学通报,2010,55(27-28):2667-2674.

Study on Characteristics of High Order Clustering for Collaboration Network

YANG Zhong-ming1,LIANG Ben-lai2,QIN Yong3,LU Qing-wu4

(1.College of Computer Engineering and Technique,Guangdong Polytechnic of Science and Technology, Zhuhai 519090,China; 2.College of Information Engineering,Zhongshan Polytechnic,Zhongshan 528404,China; 3.College of Computer Science,Dongguan University of Technology,Dongguan 523808,China; 4.Information Technology Center,Huizhou University,Huizhou 516007,China)

The research made in the field of information science shows that scientific collaboration relationship network formed by the researchers is unconnected.While the characteristics of scale-free network and small-world network presented from the network statistical parameter shows that collaboration network is a typical network describing the scientific collaboration research.The concept of high order clustering coefficient is presented.With the use of network data of journal authors,it will calculate journal collaborators’ high order clustering coefficientC(h),andformachartandanalyzethesignificanceofC(h)inthechart.Theanalysisofalargeamountofcollaborator’sampledatacollectedfromthefirst-classdomesticjournalofcomputershowsthatwhenthenumberofcollaboratorsisaround20,thecooperationteamhasextensiveknowledgeandahighlevelofcooperationanditiseasierfortheteamtomakeahighlevelofinnovativeachievement.Thatmeansahigh-levelauthorwillusuallykeepacooperativerelationshipwithabout20scholarsdirectlyorindirectly.

cooperation networks;small world network;high order clustering coefficient;average distance

2016-03-06

2016-06-15

时间：2016-11-22

国家自然科学基金资助项目(61170193)；广东省工业高新技术领域科技计划项目(2013B010401036)；广东省高等学校优秀青年教师培养计划项目(YQ2014187)；广东省自然科学基金项目(S2013010015940)；广东省教育厅科技创新项目(2013KJCX0178)

杨忠明(1980-)，男，硕士，副教授，CCF会员，研究方向为计算机网络、智能算法。

http://www.cnki.net/kcms/detail/61.1450.TP.20161122.1227.018.html

TP

A

1673-629X(2017)02-0200-05

10.3969/j.issn.1673-629X.2017.02.046