基于嵌入式的智能搜救无人机飞控系统设计

卢清秀

(广东工业大学华立学院，广东 广州 511325)

基于嵌入式的智能搜救无人机飞控系统设计

卢清秀

(广东工业大学华立学院，广东 广州 511325)

针对当前搜救无人机飞控系统控制性能差的问题，基于嵌入式平台进行了搜救无人机的飞控系统设计，以提高搜救无人机的飞行稳定性，并提出一种基于LM-Smith神经网络泛函的搜救无人机飞行控制算法。飞控系统设计主要包括控制算法设计和硬件模块设计两大部分，采用最小信息熵进行LM-Smith神经网络泛函加权，对被控对象进行模式识别和稳定性自适应修正，对飞行控制的位置偏移进行完全跟踪补偿，通过构建的LM-Smith神经网络泛函的控制器，获得渐进稳定收敛的飞行控制算法。以S3C2440A ARM9处理器作为控制核心和以Micro2440为核心主控板，基于嵌入式Linux系统加载控制程序，实现了控制系统改进设计。为验证飞控系统与控制算法的有效性和适用性，进行了性能测试与分析。测试结果表明，所构建的飞控系统在智能搜救无人机飞行控制中具有较高的轨迹跟踪控制精度，姿态稳定性和控制性能较好。

嵌入式；搜救无人机；飞控系统；控制算法；神经网络

0 引 言

随着机械自动化制造技术和人工智能技术的发展，无人机得到了一定的发展，无人机的稳定性飞行控制一直是制约其发展的一个重要瓶颈。智能搜救无人机作为一种新型的无人飞机，在未来的野外探测、军事侦察、遥感监测和探险考察等领域都会有较好的应用价值。智能搜救无人机的气动特性导致飞行姿态不稳定性，需要通过飞机惯导设计进行扰动抑制，防止飞机翻滚和失衡，因此研究智能搜救无人机的飞控系统设计方法，对提高飞机的稳定性和平衡性具有重要意义[1]。

在嵌入式平台下进行搜救无人机的飞控系统设计，智能搜救无人机的气动特性导致飞行姿态不稳定性，需要通过飞机惯导设计进行扰动抑制，防止飞机翻滚和失衡[2-3]。传统方法中，对搜救无人机的飞控系统设计主要是在控制算法和控制系统设计上进行深入研究，其中，文献[4]提出了一种基于模糊神经网络控制的智能搜救无人机的飞行控制方法，基于能量反演镇定函数非线性跟踪制导进行飞控算法设计，然后在Linux嵌入式内核平台中进行系统集成，提高了飞控系统的稳定性。但是该方法具有计算开销较大、实时性不好的问题。文献[5]提出了一种基于惯导失衡补偿的无人机飞控系统设计方法，采用最小信息熵泛函方法进行反演控制，能够基本满足姿态控制的需求。但该飞控系统在受到气流的强扰动下对无人机的搜索角度提出了较为苛刻的要求，导致控制性能不好[6]。

针对上述问题，对传统的搜救无人机的飞控系统设计方法进行改进，在嵌入式平台下进行无人机飞控系统设计，并改进了控制算法设计，提出一种基于LM-Smith神经网络泛函的搜救无人机飞行控制算法。在嵌入式平台下进行了飞控系统的模块化设计以及主控芯片集成设计。仿真实验与性能测试结果表明，所构建的飞控系统有效可行，在提高搜救无人机的控制性能和飞行稳定性控制精度方面具有较为显著的优越性。

1 智能搜救无人机控制算法设计

1.1 智能搜救无人机飞控系统的控制原理

为了进行智能搜救无人机的飞控系统设计，提高飞行稳定性和姿态自校正性能，采用的是最小信息熵的LM-Smith神经网络泛函稳定性控制模型[7]。假设在D维搜索空间中，智能搜救无人机飞控系统的控制渐进稳定性的状态函数为：

(1)

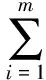
(2)

根据Hopfield网络极大熵准则[8]，对一定的范围内按照自身姿态误差时变的时滞函数，控制系统的输入基函数分别为d1(t)和d2(t)，其满足：

0≤d1(t)≤h1<∞,0≤d2(t)≤h2<∞

(3)

(4)

其中，h1,h2,τ1与τ2为正常量。

在飞控系统设计中，由确定性方程得到的具有随机性的运动状态，通过实时自适应学习算法对被控对象进行辨识，得到飞控状态函数：

(5)

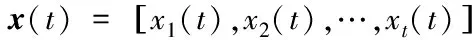
根据上述给出的智能搜救无人机飞控系统的控制原理，进行控制算法和控制系统设计。

1.2 智能搜救无人机控制算法改进设计

在上述控制原理的基础上，进行控制算法设计，提出了一种基于LM-Smith神经网络泛函的搜救无人机飞行控制算法，采用最小信息熵进行泛函加权得到智能搜救无人机的位姿状态信息，定义d(t)=d1(t)+d2(t)，得到智能搜救无人机的飞控系统的状态跟踪连接权值为：

(6)

其中，Gc(s)和G0(s)为适当维数的归一化定标因子矩阵，计算飞控系统前馈神经网络的权值和阈值，通过规范权值点函数，训练FNNs，得到飞控系统神经网络的第一层全局最优位置为：

(7)

当满足上述条件下，得到的LM-Smith神经网络系统有较大的Lyapunov指数。为了满足稳定性条件[9-10]，采用无限折叠迭代混沌映射得到飞控系统的状态参量d1(t)和d2(t)，合并成一个时滞d(t)，得到：

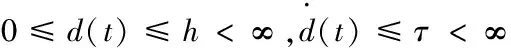
(8)

更新智能搜救无人机的速度Vi和位置Xi，系统可写为：

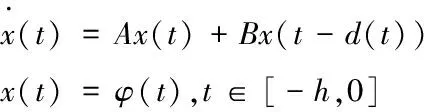
(9)

利用前述现有的稳定性条件，以全局最优智能搜救无人机的位置Xggbest为初始点，得到LM-Smith神经网络泛函的控制器的结构，如图1所示。

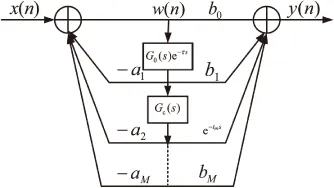
图1 LM-Smith神经网络泛函的控制器的结构

上述控制结构中，G0(s)e-τs是平衡位置与外力矩耦合的惯导函数，Gc(s)是初始化后的LM-Smith神经网络系统[11]，Gm(s)与e-tms是搜救无人机质心在地面上的投影权值和偏值初始函数。智能搜救无人机三通道模型的权值和偏转向量时滞不相关时，Gm(s)=G0(s)，tm=τ，得到控制参量的反馈信号为：

H(s)+Y(s)=Gm(s)U(s)

(10)

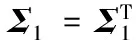
(11)

显然当pk=-gk时，F(xk+1)对于LM-Smith神经网络泛函的迭代优化公式为：

xk+1=xk-αgk

(12)

其中，α是学习速率。

通过上述设计，可见设计的控制算法是渐进稳定的。

2 基于嵌入式平台的无人飞控硬件设计

在上述控制算法设计的基础上，基于嵌入式Linux系统，进行飞控系统的硬件模块设计。在ARM为核心的计算机系统中使用ARM，PowerPC，以及一些嵌入式DSP系统，进行飞控系统的集成设计。飞控系统内的主控芯片采用的是嵌入式AD9225[13]，AD9225是AD公司一款高性能A/D芯片，单5V供电，分辨率12位，最大采样频率25MHz。首先进行A/D电路设计，数字电源采用数字3.3V供电，采用10μF、0.1μF和0.001μF的电容并联来滤除不同频率的噪声。为满足MOSFET半桥功率分配的需求，在飞行控制的状态识别中，采用双通道双向电平转换ADG3301在3.3～5V的电平转换传输时延为6ns，使得ADCLK相比PPI-

CLK延迟6ns,采用π型滤波，减少电源毛刺，设计高性能运放，降低电路底噪声。在飞控系统设计中，需要进行A/D电路设计，负责对调理后的接收和参考信号进行采样，送入DSP内处理。在EEPROM设计中，当检测到飞行控制异常时，驱动蜂鸣器发出报警信号。系统在选择数字信号处理器时考虑如下两方面：

(1)运算能力。运算能力是考察整个飞控系统的智能处理速度和能力的重要特征，在嵌入式平台下，飞控系统采用2个40位ALU，4个8位视频ALU进行高频数学运算，实现快速处理与实时处理的关键因素[14]。选择的数字信号处理器应该满足系统对计算速度的要求。

(2)指令系统。由于飞控系统的控制指令复杂，需要简洁而功能强大的指令系统，芯片选择Blackfin系列中的高性能产品，有利于系统编程，对智能搜救无人机的飞控系统开发有利。

综上分析，在飞控系统设计过程中，指标性能满足：

(1)2个通道全双工同步串行接口，峰值运算能力可达2.4GMAC/s；

(2)12个通用32-bit定时/计数器，支持PWM；

(3)支持IrDA(InfraredDataAssociation)的UART，2个对称的600MHz高性能Blackfin内核；

(4)内核电压0.8～1.2V，片内调压器可调。

在上述系统的指标性能分析和芯片选择的基础上，在嵌入式平台进行飞控系统的主控电路设计，使用的宿主机是Intelx86构架的PC机，嵌入式软件系统的开发通常采用交叉编译环境，即开发环境安装在桌面或者服务器计算机系统，表征数字信号处理器处理能力的重要标志，再通过网线、232串口、USB等方式将程序下载至嵌入式系统中。控制算法加载过程如图2所示。

在无人机飞控系统的网络通信模块中，通过LEEP帧的信息来估计EETX值，每当收到一个LEEP帧，会触发SubReceive.receive()事件。

3 实验与结果分析

为了测试设计的智能搜救无人机飞控系统在优化飞行控制，提高飞机稳定性和平衡性方面的性能，进行仿真实验。实验的硬件平台：CPU采用三星S3C2440，运行于400MHz。NORFLASH为2M，嵌入式平台采用可支持ARM-Linux(内核版本Linux-2.6.32.2)、

图2 飞控系统的控制算法程序执行流程

WindowsCE5.0/6.0、uCos2的S3C2440AARM9处理器，控制算法采用Matlab进行数学编程，使用JTAG板(一般借助H-JTAG软件)直接烧写入NorFlash进行控制算法的程序读写。飞控系统的姿态稳定性控制中，进行姿态特征采样，采样时间为13ms，起始频率为35kHz，带宽为20kHz。无人机飞行控制模型状态离散方程为：

y(k)=0.579 6y(k-1)+0.399u(k-5)+0.021 46u(k-6)

(13)

y(k)=0.472 4y(k-1)+0.633 2u(k-1)

(14)

飞行控制的频率变化范围为23～40kHz，LM-Smith神经网络泛函控制参数如下：

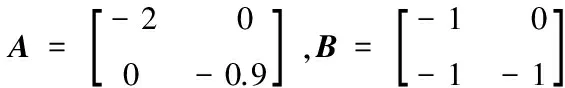
(15)

在上述仿真环境和参数设定的基础上，采用设计的控制算法和控制系统进行飞行控制稳定性测试。首先输入测试信号，测试飞控系统进行轨迹跟踪的性能，进行搜救无人机的轨迹跟踪性能测试，输出结果如图3所示。

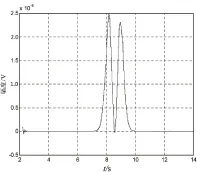
图3 飞控系统轨迹跟踪控制输出

由图3可见，Pd=0.995，Pf=0.000 1,满足无人机姿态跟踪识别和控制的精度要求，系统抗干扰信噪比满足：d≥16.57dB。采用文中设计的飞控系统进行智能搜救无人机的轨迹跟踪，具有较准确的姿态和轨迹跟踪性能，提高了控制精度，展示了该系统的优越性。

4 结束语

智能搜救无人机的气动特性导致飞行姿态不稳定性，需要通过飞机惯导设计进行扰动抑制，以防止飞机失稳。因此，智能搜救无人机飞控系统设计方法的研究，对提高无人机的稳定性和操纵性具有重要意义。为此，在嵌入式平台下进行了搜救无人机的飞控系统设计与实现，以提高搜救无人机的飞行稳定性。在控制算法设计中，提出了一种基于LM-Smith神经网络泛函的搜救无人机飞行控制算法；在飞控系统的模块化设计中，基于嵌入式平台进行了飞控系统主控芯片集成设计。仿真与测试结果表明，所构建的飞控系统应用在无人机飞行控制中，具有较高的轨迹跟踪控制精度，实现了无人机的稳定性控制。

[1] 孙克辉,贺少波,董燕青.简化洛伦兹混沌系统的追踪同步控制[J].信息与控制,2015,44(4):393-397.

[2]MahmoudEE.Complexcompletesynchronizationoftwononidenticalhyperchaoticcomplexnonlinearsystems[J].MathematicalMethodsintheAppliedSciences,2014,37(3):321-328.

[3]MathenyMH,GrauM,VillanuevaLG,etal.Phasesynchronizationoftwoanharmonicnanomechanicaloscillators[J].PhysicalReviewLetters,2014,112(1):014101.

[4]NjahAN.TrackingcontrolandsynchronizationofthenewhyperchaoticLiusystemviabacksteppingtechniques[J].NonlinearDynamics,2010,61(1-2):1-9.

[5]ChenG,LewisFL.DistributedadaptivetrackingcontrolforsynchronizationofunknownnetworkedLagrangiansystems[J].IEEETransactionsonSystems,Man,andCybernetics,PartB:Cybernetics,2011,41(3):805-816.

[6]SunKH,LiuX,ZhuCX.Dynamicsofastrengthenedchaoticsystemanditscircuitimplementation[J].ChineseJournalofElectronics,2014,23(2):353-356.

[7] 宋申民,郭 永,李学辉.航天器姿态跟踪有限时间饱和控制[J].控制与决策,2015,30(11):2004-2008.

[8]GuoY,SongSM.Adaptivefinite-timebacksteppingcontrolforattitudetrackingofspacecraftbasedonrotationmatrix[J].ChineseJournalofAeronautics,2014,27(2):375-382.

[9]ChutiphonP,PimchanaS.Nonsingularterminalslidingmodebasedfinite-timecontrolforspacecraftattitudetracking[J].InternationalJournalofControl,AutomationandSystems,2014,12(3):530-540.

[10] 李贵明,刘良栋.刚体卫星姿态的有限时间控制[J].空间控制技术与应用,2011,37(3):1-8.

[11] 徐为民,徐 攀.不确定扰动下双起升桥吊双吊具鲁棒自适应滑模同步协调控制[J].控制与决策,2016,31(7):1192-1198.

[12] 陈海燕,刘 威,李 莉.相对相位噪声对相干光通信系统性能影响[J].激光技术,2016,40(1):94-98.

[13] 王 勋,张代兵,沈林成.一种基于虚拟力的无人机路径跟踪控制方法[J].机器人,2016,38(3):329-336.

[14]MahboubiH,MoezziK,AghdamAG,etal.Distributeddeploymentalgorithmsforimprovedcoverageinanetworkofwirelessmobilesensors[J].IEEETransactionsonIndustrialInformatics,2014,10(1):163-174.

Design of Flight Control System for Intelligent Search and Rescue UAV with Embedded System

LU Qing-xiu

(Huali College of Guangdong University of Technology,Guangzhou 511325,China)

In order to solve the problem of poor performance of unmanned rescue flight control system,the flight control system of unmanned rescue has been designed for lift of its flight stability.A flight control algorithm suitable for flight control system of the intelligent search and rescue UAV has also been proposed based on LM-Smith neural network,which mainly includes two parts,design of control algorithm and that of hardware module.The LM-Smith neural network functional weighted method with minimum information entropy has been employed for pattern recognition of controlled object and self-adaptive modification of flight stability.The location offsets in process of flight control has been tracked and compensated wholly.And thus asymptotically stable convergence of the proposed flight control algorithm has been achieved via established functional controller with LM-Smith neural network.The promoted design of flight control system has been implemented by adopting S3C2440A processor as control core and processing and ARM9 as core main control board and loading embedded Linux system as control program.The tests and analysis have been conducted to verify effectiveness and applicability of both the established flight control system and the designed flight control algorithm.The test results show that the established flight control system has higher precision of trajectory tracking and control,better attitude stability and control performance.

embedded;unmanned rescue machine;flight control system;control algorithm;neural network

2015-11-19

2016-04-05

时间：2017-01-10

2012广东省质量工程项目(粤教高函[2012]204号)；2015年广东省教育重点平台及科研项目青年创新人才类项目(自然科学类)(2015KQNCX218)

卢清秀(1979-)，女，硕士，讲师，研究方向为计算机控制算法、人工智能。

http://www.cnki.net/kcms/detail/61.1450.TP.20170110.1010.040.html

TP271

A

1673-629X(2017)02-0191-04

10.3969/j.issn.1673-629X.2017.02.044