在物理课堂教学中渗透数学思维方法——“运动快慢的描述——速度”拓展习题

张 宇，聂 妍，肖天华

(1.佳木斯大学 理学院，黑龙江 佳木斯 154007；2.佳木斯第三中学，黑龙江 佳木斯 154007)

在物理课堂教学中渗透数学思维方法
——“运动快慢的描述——速度”拓展习题

张 宇1，聂 妍1，肖天华2

(1.佳木斯大学 理学院，黑龙江 佳木斯 154007；2.佳木斯第三中学，黑龙江 佳木斯 154007)

物理教学中渗透数学思维方法对学生学好物理具有极其重要的作用。总结出一些帮助学生提高在物理学习中运用数学能力的策略，并通过研究高中物理拓展习题教学案例，从实践的角度探究如何在物理教学中渗透数学思维方法。

物理课堂教学；渗透；数学思维方法；拓展习题

在物理教学中渗透数学思维方法不仅能够帮助学生更好地学习物理，而且能提高学生综合运用学科知识解决问题的能力。

一、物理教学中渗透数学思维方法的策略

(一)让学生正确认识数学在物理学习中的重要作用

让学生明确数学在物理中的重要作用，知道数学有利于物理问题的定量分析、物理概念规律的精确表述，让学生有意识地在学习物理前打好数学基础。与此同时，教师也要注意不能夸大数学在解决物理问题时的作用，避免把物理问题数学化。例如，有些学生在用数学公式解答物理习题的时候，没有仔细思考公式所表达的物理量之间的因果关系，导致无法成功解题或解答错误。

(二)帮助学生建构数学模型

在物理教学中，培养学生的创新精神和实践能力特别重要，这一切都离不开物理建模能力的培养。如何帮助学生理解生活中的物理问题，建立起物理模型，是中学物理教学重点，也是难点。在教学中渗透数学思维方法时，可以引导学生将物理模型转化为数学模型；建立物理模型后，启发学生找出相关物理量，并用符号、字母、数字等数学语言表示这些物理量，引导学生建立数学模型，列出所研究物理问题的相关特性以及量与量之间关系的数学表达式，从数学模型出发将各个物理量构建联系。

(三)培养学生运用数学语言来表述物理概念、规律的能力

数学语言主要包括符号、字母、数字、图像、图表等。中学物理所学习的概念和规律常用数学语言、公式来表达。在教学中应该鼓励学生使用合适的数学语言来表述物理概念和规律，进一步写出数学表达式。在学习概念和规律时，应该通过对公式、文字表达的分析，强调其物理意义，理解公式所描述的物理事实和物理现象之间的因果关系。但要注意防止学生将物理公式按单纯的数学关系理解。

(四)在实验教学中培养学生运用数学方法探究物理规律的能力

在实验教学中，应该启发学生通过对实验数据的分析，发现变量、定量之间蕴含的数学联系，也可以通过绘制图像来帮助发现关联，并让学生独立思考，总结表述出物理规律。要培养学生运用数学语言表述物理规律的能力，进一步培养学生通过数学方法独立分析、总结物理规律的能力。这样不仅能够加深学生对于物理过程、物理规律的记忆和理解，更有助于培养学生的创新精神和实践能力。

二、运动快慢的描述拓展习题

(一) 教学片段：人教版物理课程必修一第一章第三节：运动快慢的描述——速度

习题：一条小船停放在一条足够长的小河的岸边。拴船的缆绳突然断开，由于风和水流的作用，小船以2.5km/h的速度，沿与河岸成15度角的方向漂走。与此同时，船夫从同一地点开始追赶小船，已知他在岸边跑的速度是4km/h，水中游的速度是2km/h，问船夫能否追上小船？

教师：大部分同学都能根据题意画图来帮助解题，在物理学习中，有时数学的图形能帮助简化许多问题，像这道题我们可把物理问题转化成三角形中边长、角度之间关系的问题。假设，AO所在的直线为河岸，AC所在的直线是小船漂走的方向，船夫沿AB在岸上追赶，沿BC在水中追赶。我们知道，如果船夫可以在小船之前到达C点，那么我们就说船夫可以追上小船。做辅助线CD垂直于AO。

板书：

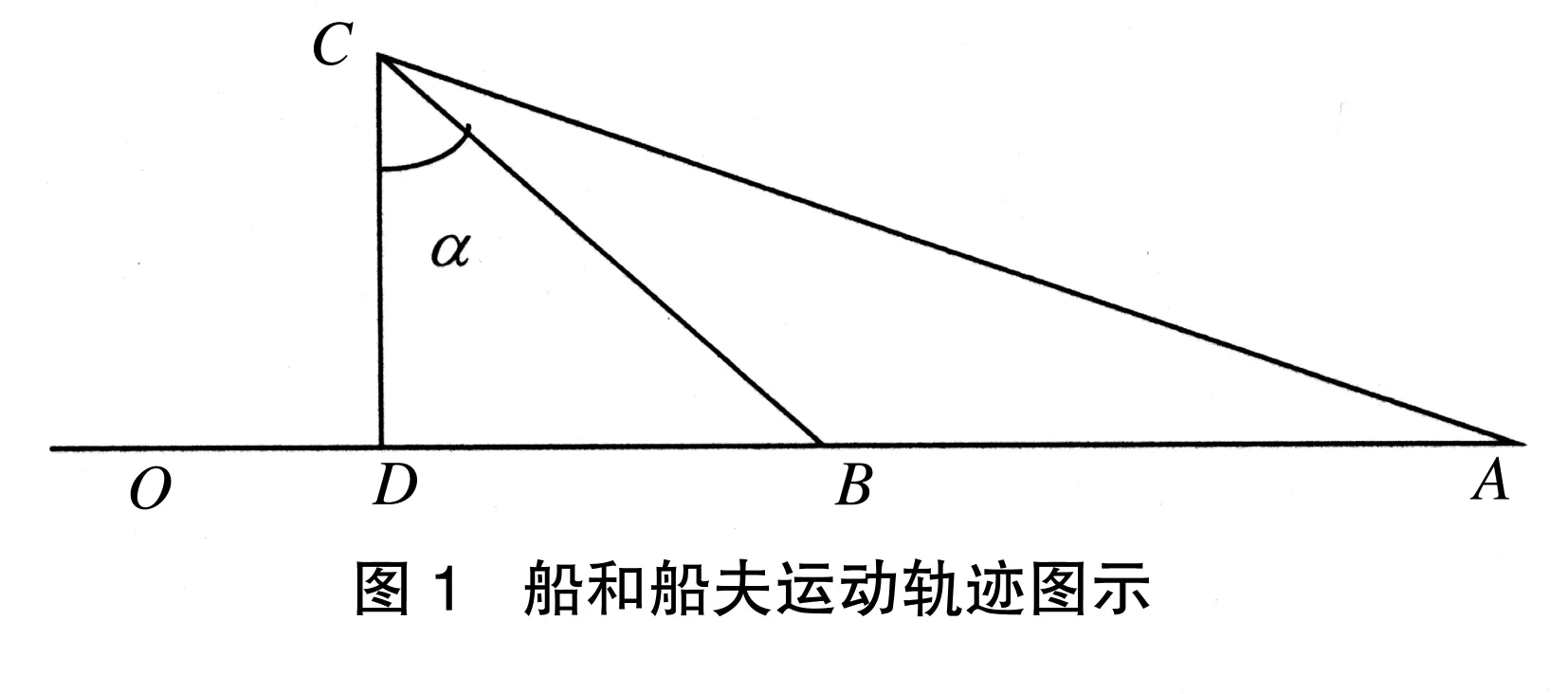
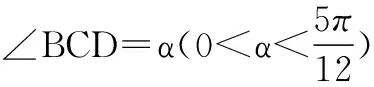
教师：假设小船到达C点需要的时间为Th，AC=2.5T。只要船夫到达C点的时间不超过Th，即能追上小船。下面我们通过求AB、BC的长度来求出船夫到达C点所需要的时间，这两段长度，我们可以通过三角函数求出。

板书：

(1)

AB=AC·cos15°-AC·sin15°·tanα

(2)

教师：知道了AB、BC的长度，已知船夫在岸上跑、水中游的速度，我们就可以写出船夫所用时间的函数表达式了。

板书：

(3)

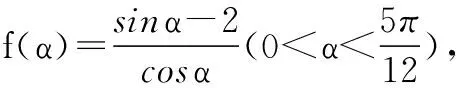
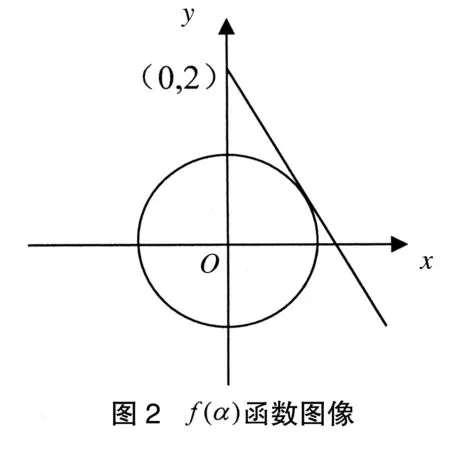
板书：

板书：

(4)

教师：通过比较，我们发现t的最小值小于T，即船夫可以追上小船。通过这道习题的解决，我们发现，把船夫所用的时间转化为三角形的边长问题就很容易列式，函数的最小值问题用图像来观察变得形象又容易……这种把直观的几何图形和抽象的数学语言、数量关系结合起来简化问题的方法，就是我们经常提到的数形结合。这种方法在物理学习中经常能够用到，学生在平时的练习中可以试着用图形来代替一些数量关系，尽量简化做题时的思维过程和求解过程。

(二)教学反思

本题包含的数学知识比较多元化，小船运动的位移，船夫在水中游、岸边跑的位移的计算要运用到数学课程中的三角函数知识，求最小值的过程中则应用了高中数学课程的三角函数知识，时间的计算和比较主要用到不等式和函数。求船夫所用时间最小值时涉及了数形结合的数学思维方法，将函数最小值问题转化到图像中去解决，这一过程中，学生是否能提取并简化所求函数中的变量，画出它的图像是渗透数形结合方法的关键，教师可以在教学前做好数学知识准备，带领学生回忆初中时学习的关于函数的几种表达形式、函数的截距式、斜率公式等。在教学过程中用到了两种渗透数学思想方法的策略。一是建构数学模型，本题中涉及的物理知识点并不难，主要是速度公式的熟练应用，但学生是否能在解决问题的最初建构数学模型，将追及问题转化到三角形中解决是教学的关键。二是培养学生运用数学语言来表述物理概念、规律的能力。建构数学模型之后，引导学生将题目中的已知条件用数学语言表达出来，例如用三角形边长的长度代替运动的位移。学生抽象问题以及表述问题的能力需要在平时进行有针对性的训练，不是一蹴而就的。

数学对于表述物理学、创造和发展物理学理论，有着很大的作用。在中学生学习物理课程的过程中，数学也是学生解决物理问题的基本工具。在大学物理理论与实验的学习中数学思维方法与物理学的结合，同样有利于学生科学素养的培养，无论对于学生今后的学习，还是从事科学研究、进行个人决策、参与社会事务都有着重要的意义。

〔责任编辑：李海波〕

Permeation of Mathematical Thinking Method into Physics Classroom Teaching——“The Description of the Movement Speed — Speed” Expanding Exercises

ZHANG Yu1， NIE Yan1， XIAO Tian-hua2

(1.College of Science, Jiamusi University, Jiamusi 154007, China； 2.Jiamusi No.3 Middle School, Jiamusi 154007, China)

The penetration of mathematical thinking method into physics teaching plays an extremely important role in students learning physics well. This article summarizes some strategies to help students improve their ability to use mathematics in physics learning. And from the angle of practice it explores how to permeate mathematical thinking method in physics teaching through the study of high school physics to expand exercises teaching cases.

physics teaching； permeate； mathematics thinking methods； expanding exercises

2016-11-20

佳木斯大学教科研课题(JKC2012-023)

张宇(1977—)，女，黑龙江佳木斯人，讲师，硕士，从事物理教学研究。

10.3969/j.issn.1008-6714.2017.02.034

G633.7

A

1008-6714(2017)02-0073-02