S-S型旋翼末敏弹气动特性规律研究

吕胜涛，季丹丹，刘荣忠，郭锐，马晓冬

(1.南京理工大学 化工学院，江苏 南京 210094；2.南京理工大学 机械工程学院，江苏 南京 210094)

S-S型旋翼末敏弹气动特性规律研究

吕胜涛1，季丹丹1，刘荣忠2，郭锐2，马晓冬2

(1.南京理工大学 化工学院，江苏 南京 210094；2.南京理工大学 机械工程学院，江苏 南京 210094)

无伞末敏弹的稳定尾翼在母弹开舱前包裹于子弹外壁，因威力要求，子弹直径需要尽可能大，导致稳定尾翼的厚度较小，而末敏子弹下落速度较快，尾翼极易在空气动力的作用下发生挠曲变形。为深入分析尾翼结构参数对末敏弹气动特性及尾翼挠曲变形的影响规律，采用双向流体- 固体耦合方法对S-S型旋翼末敏弹进行分析。研究结果显示：末敏弹阻力系数随弯折角α21的增大呈递增趋势，而随其余3个弯折角的增大呈递减趋势；转动力矩系数随4个弯折角的增大均呈递增趋势，随4个弯折比的增大均呈现准线性递增趋势，随两翼长宽比的增大呈递减趋势。高塔自由飞行试验结果表明，末敏弹阻力系数和转动力矩系数的仿真误差分别不超过7.8%和6.1%，证明了双向流体- 固体耦合方法分析无伞末敏弹气动特性的可行性与正确性。

兵器科学与技术；末敏弹；气动弹性；气动特性；流体- 固体耦合；自由飞行试验

0 引言

经历了第一次世界大战的初露锋芒，自第二次世界大战开始，坦克等装甲战车确立起在现代地面战争中的霸主地位，为占据现代战争中的主导优势，世界各军事大国积极开展了对反坦克武器的研制工作[1]。以聚能射流为毁伤元素的破甲弹[2]和以动能侵彻为毁伤手段的杆式穿甲弹[3]在打击常规装甲坦克上取得了骄人的成绩，但随着防护技术的迅速发展，诞生了大量的新型装甲防护如反应装甲、复合装甲、陶瓷装甲等，极大地削弱了以正面、侧面装甲为打击点弹药的毁伤效能[4-5]。与此同时，各类智能、新型弹药也逐渐问世。药型罩以聚能装药原理形成的爆炸成型弹丸(EFP)[6]在目标装甲厚度较小时表现出良好的侵彻能力与靶后效应，已普遍应用于各类智能弹药。于是，一种采用EFP战斗部专门打击坦克顶部薄弱装甲的新型弹药——末端敏感弹药(简称末敏弹)，成为世界反坦克武器中的新星[7]，其中以美国研制的SADARM[8-10]末敏弹，德国研制的SMArt末敏弹，瑞典法国联合研制的BONUS[11]末敏弹为典型代表。

20世纪70年代，美国首先提出末敏弹的概念，之后很长一段时间里均采用涡环伞作为末敏子弹的减速减旋及稳态扫描平台，伞衣充分展开后面积较大，可为末敏子弹提供很大的阻力，减缓其下落速度，对早期并不十分先进的毫米波、红外等敏感器要求不高，给予其充分的扫描探测时间。但也正因如此，装甲目标拥有足够长的反应时间对末敏子弹进行干扰甚至反击。此外，涡环伞末敏弹极易在环境横风的影响下发生“随风飘”的情况，使子弹偏离目标区域以至无法准确扫描目标，极大降低了子弹对装甲目标的捕获概率及命中概率。针对涡环伞末敏弹的劣势，一种以金属尾翼作为弹体稳态扫描机制的旋翼末敏弹，引起了各国的重视。旋翼末敏弹采用迎风面积更小的金属尾翼为弹体减速，下落速度较快，极大地降低了横风的影响，且不易被敌方拦截。

旋翼末敏弹完成既定战斗任务的前提是实现稳态扫描运动，即下落过程中维持稳定的落速、转速和扫描角。圆柱形弹体难以为弹体提供稳定的阻力和转动力矩[12]，这就需要金属尾翼为末敏子弹提供尽可能大的阻力以延长其滞空时间，为弹载敏感器提供充足的扫描探测时间；同时，尾翼需要提供足够大的转动力矩以维持末敏弹的稳定转速，保证敏感器在地面上的扫描线形成阿基米德螺旋线，提高子弹对目标的捕获概率。国外许多学者研究了末敏弹的气动特性及运动特性，但由于技术保密，关于旋翼末敏弹动力学建模和动力学特性分析方面的书籍、文献资料等并不多见[13-15]。近年来，随着计算流体力学(CFD)的迅速发展，国内对旋翼末敏弹的仿真及试验研究方法得以更新和扩充。舒敬荣等[16]在分析质量分布非对称力学表示方法的基础上，建立了末敏弹动力学模型，编制了模型的仿真计算软件。胡志鹏等[17]采用CFD方法分析旋翼末敏弹，获得了流场特性、末敏弹表面压力分布和阻力系数、升力系数等气动参数随攻角的变化规律，并通过自由飞行试验对平板尾翼和S-C型尾翼末敏弹进行了动态气动特性研究。郭锐等[18]设计了一种非对称双翼结构末敏弹的高塔投放试验，通过改变尾翼形状、面积及布局，分析了非对称双翼结构对末敏弹实现减速导旋性能的影响。吕胜涛等[19]基于CFD和正交优化方法对S-S型双翼末敏弹进行了尾翼结构的优化设计，得到了满足最大阻力系数和最大转动力矩系数的末敏弹尾翼结构。周志超等[20]提出轴向折叠和径向折叠两种尾翼类型的末敏子弹气动外形结构，设计了末敏弹模型和实验装置，进行了小迎角低速风洞实验，获得了模型分别在固定和旋转条件下的气动力数据，测量了模型在空气动力作用下的转速，并对模型的稳定性进行了分析。舒敬荣等[21]针对旋翼末敏弹稳态扫描时做大攻角圆运动的特点，求取了其在一般形式赤道阻尼力矩作用下攻角方程的近似解析解，在此基础上运用振幅平面法分析旋翼末敏弹的运动稳定性。赵博博等[22]针对掠飞末敏弹新型扫描机理的作战效能进行评估，研究末敏弹在弹道末段的捕获特性。综上所述，国内外学者分析旋翼末敏弹气动特性时大多将尾翼视为刚性体，随着模拟手段的丰富及研究方法的完善，对末敏弹尾翼气动弹性及其对末敏弹气动特性影响规律的研究十分迫切，将有助于提高旋翼末敏弹尾翼结构的设计精度，而国内外在此方面的研究报道并不多见。

受限于母弹的装填空间及末敏子弹的直径要求，旋翼末敏弹稳定尾翼的厚度通常不超过1 mm，而末敏弹稳态扫描阶段的下落速度可达到30 m/s，末敏弹尾翼在空气动力作用下极易发生一定程度的挠曲变形，变形后的尾翼将会对末敏子弹周围流场产生影响，流场的变化反过来又进一步影响了尾翼的变形。这一过程将对末敏弹的气动特性产生一定的影响，使其实际运动参数与设计参数发生偏差。旋翼末敏弹尾翼的结构参数众多，有必要深入分析各参数对旋翼末敏弹气动特性以及尾翼挠曲变形的影响规律。

1 计算模型

1.1 旋翼末敏弹结构

如图1所示，S-S型末敏弹采用两片S形金属尾翼作为弹体的稳态扫描机制，尾翼以90°安装角固定于弹尾部，结构参数不同的两翼可为弹体提供阻力，稳定其落速，同时尾翼可为末敏弹提供转动力矩，保证末敏弹的转速。

图1 S-S型旋翼末敏弹计算模型Fig.1 Simulation model of S-S-shaped TSP

1.2 分析方法

末敏弹弹体为圆柱体，直径110 mm，高135 mm，两S形翼厚度均为1 mm. 流场为边长2000 mm的立方体，末敏弹弹体模型位于流场的中心，如图2和图3所示。

图2 弹体网格划分Fig.2 Grid generation of TSP

图3 流场网格划分Fig.3 Grid generation of flow field

采用ANSYS WORKBENCH双向流固耦合方法对旋翼末敏弹气动特性进行分析，仿真过程为：采用CFX对末敏弹流场进行模拟，得到的弹体表面压力数据传递给瞬态结构动力学模块进行尾翼的挠曲变形分析；对变形后的末敏弹结构重新进行流场分析，此过程反复进行，直至流体域和固体域均达到稳定状态，认为流体- 固体耦合过程结束。其中流场仿真的湍流模型采用k-ε模型，入口采用速度入口，出口采用outflow，弹体表面为壁面边界，对弹性尾翼变形导致的流场变动采用动网格技术进行处理。时间采用2阶欧拉后差格式，计算步长0.1 s，总时间5 s. 参考面积为末敏弹圆柱弹体横截面积，参考长度为圆柱弹体母线长度。对于固体域，尾翼材料选用65Mn弹簧钢，密度为7 850 kg/m3，杨氏模量为70 GPa，泊松比为0.3，流场工质采用常温标准空气，密度为1.29 kg/m3. 旋翼末敏弹的设计落速在30 m/s左右，弹轴与铅垂线的夹角，即攻角约为30°，如图4所示。

图4 末敏弹运动姿态Fig.4 Locomotion characteristics of TSP

1.3 网格无关性检验

对于CFD仿真，域网格划分越细密，计算精度越高，但网格数目过大也将延长仿真时间而降低计算效率。根据文献[22]，对于一确定模型，模型计算精度随网格数目的增大而提高，在网格数达到某一值后，计算结果趋于稳定，本文首先对不同网格数目的模型进行计算分析，以期在满足计算精度的基础上尽可能缩短计算时间。

网格划分时，弹体部分采用统一尺寸，流场域靠近弹体部分的网格密度与弹体网格密度相同，远离弹体则逐渐减小网格密度。由于末敏弹结构复杂，本文以非结构化网格对末敏弹流场进行划分。用于进行无关性检验的模型网格总数分别为50万、100万、150万、200万、250万、300万、350万和400万，分析各模型阻力系数Cd和转动力矩系数Cm随模型网格数的变化规律，如图5所示。

图5 末敏弹气动参数随模型网格数目变化Fig.5 Aerodynamic characteristics of TSP

由图5可见，模型网格数目较少时，末敏弹气动参数变化较大且无规律性，在网格数超过300万后，Cd、Cm曲线趋于平缓，故本文在进行末敏弹气动特性分析时以300万网格数目进行划分。

1.4 末敏弹尾翼结构参数

S-S型末敏弹尾翼结构参数的定义如图6所示，S10、S20分别为两翼与弹体横截面平行部分的面积，S11、S12、S21、S22分别为两翼弯折面的面积；l10、l11、l12、l20、l21、l22分别为对应的尾翼长度；w1、w2分别为两翼弦长。弯折比定义Δ11=S11/S10，Δ12=S12/S10，Δ21=S21/S20，Δ22=S22/S20，两翼长宽比定义为lw1=(l10+l11+l12)/w1，lw2=(l20+l21+l22)/w2，S-S型旋翼末敏弹弯折角定义见图7.

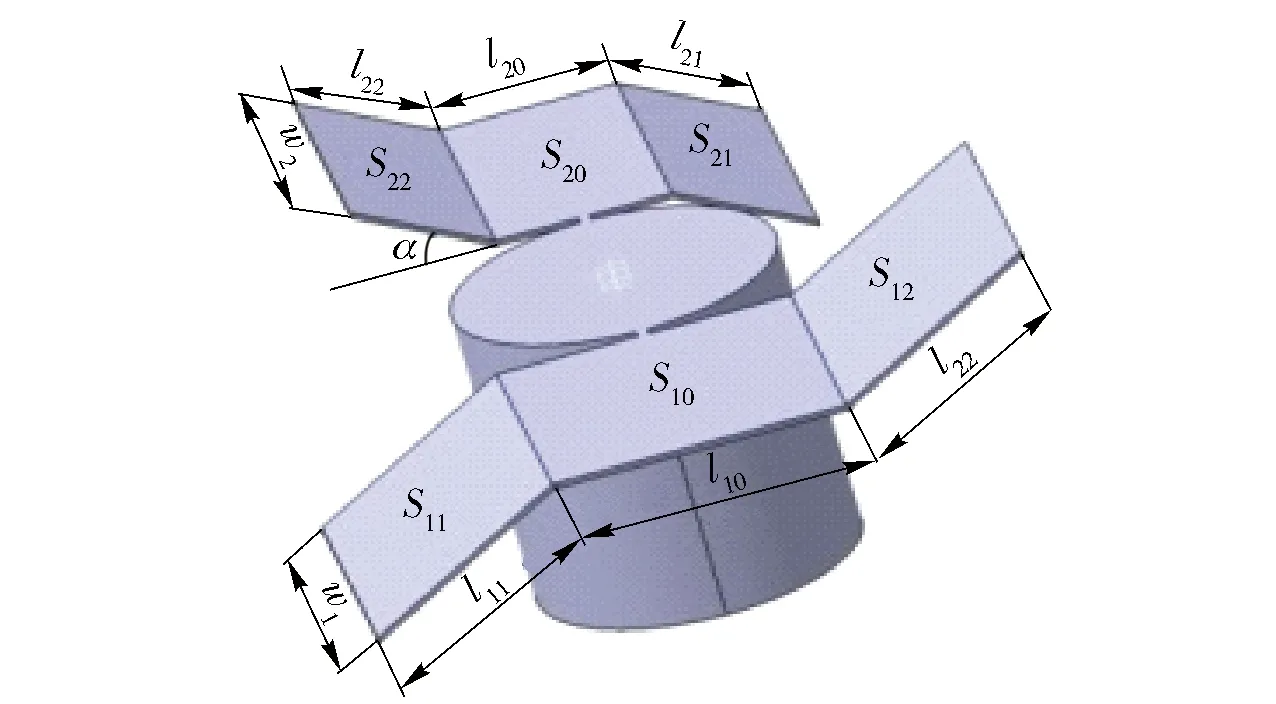
图6 尾翼结构Fig.6 Wing structure

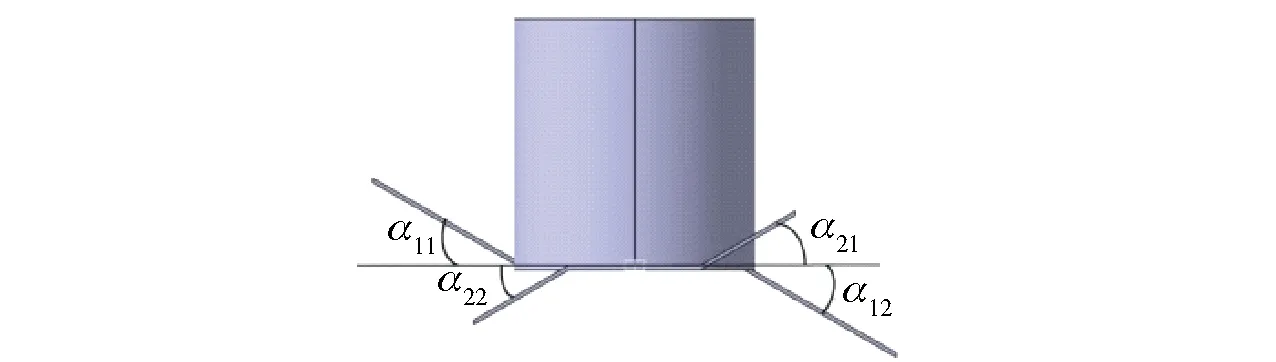
图7 尾翼弯折角Fig.7 Bending angles

2 控制方程

2.1 流体域方程

流体流动要遵循质量守恒定律和动量守恒定律。对于本文的末敏弹流场，守恒定律可通过如下控制方程进行描述。

质量守恒方程

(1)

动量守恒方程

(2)

(3)

2.2 固体域方程

固体(即末敏弹弹体)部分的守恒方程由牛顿第二定律导出：

(4)

2.3 流体- 固体耦合方程

流固耦合遵循最基本的守恒原则，故在流体- 固体耦合交界面处，应满足空气与弹体应力、位移等变量的守恒：

(5)

式中：τf为流体应力；τs为结构应力；nf为τf的法向矢量；ns为τs的法向矢量；ds为结构位移；df为流体位移。

3 结果分析

3.1 模型参数

本文计算模型的初始模型参数如下：α11=α12=α21=α22=30°，Δ11=Δ12=Δ21=Δ22=1.0，lw1=2.3，lw2=1.4. 在分析各参数对末敏弹气动特性影响规律时，保持其他参数恒定，弯折角取值范围0°～30°，间隔5°；弯折比取值范围0.7～1.3，间隔0.1；lw1取值范围2.0～2.6，间隔0.1，lw2取值范围1.1～1.7，间隔0.1.

3.2 弯折角对气动特性的影响

图8所示为尾翼弯折角对S-S型旋翼末敏弹阻力系数的影响规律，可见末敏弹阻力系数随α21的增大呈递增趋势，而随其余3个弯折角的增大呈递减趋势。参考图7，α21是较小S翼向迎风面弯折的部分，由于尾翼的气动弹性，此角度较小时，来流容易从该翼的短边处溢出，导致迎风面压力减小，阻力系数也较小。从增大末敏弹阻力系数、减小落速的角度考虑，应增大α21，减小其余3个角度值。

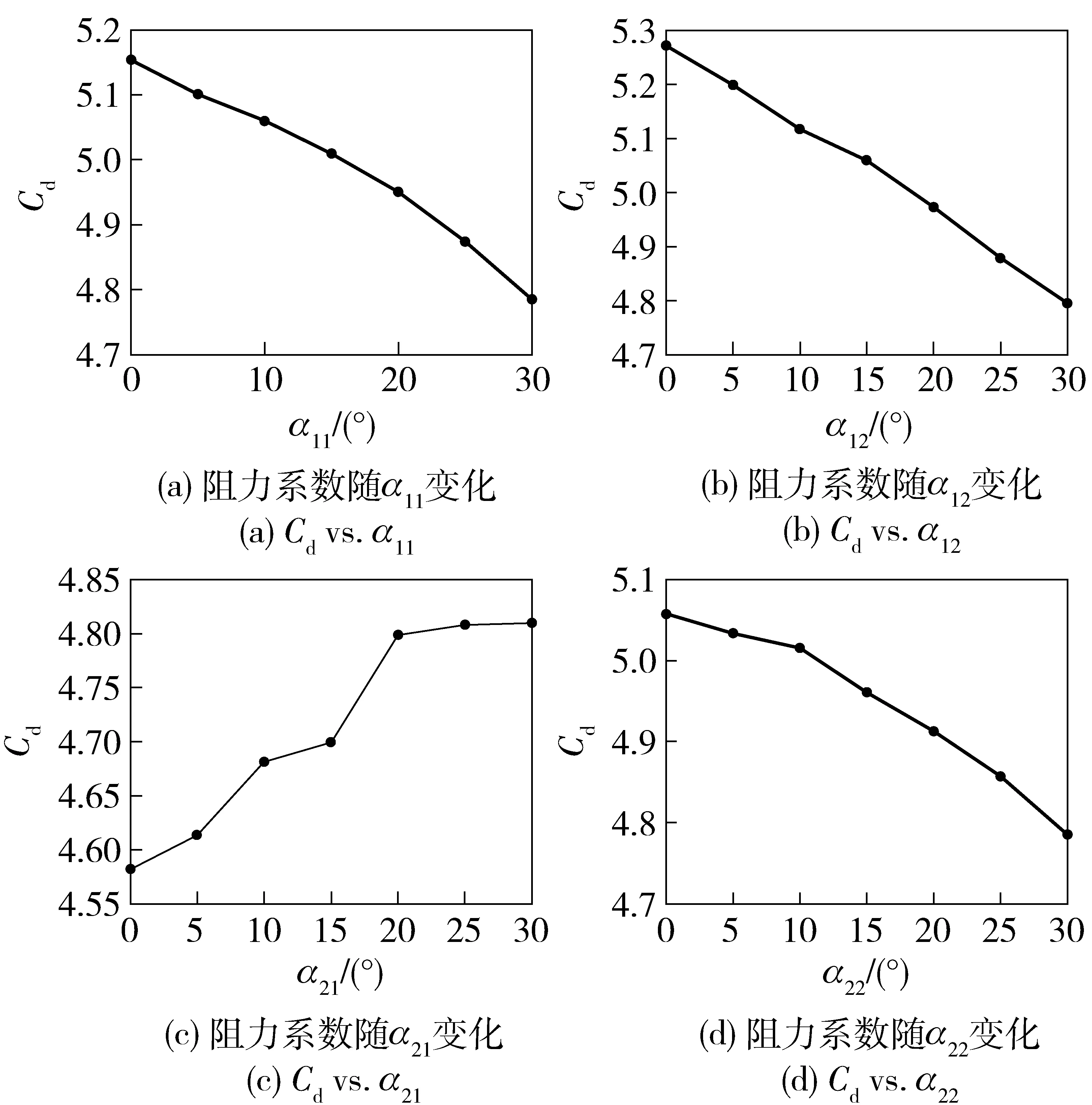
图8 弯折角对阻力系数的影响规律Fig.8 Cd vs. bending angle

图9所示为尾翼弯折角对S-S型旋翼末敏弹转动力矩系数的影响规律，可见末敏弹转动力矩系数随4个弯折角的增大均呈递增趋势。根据文献[23]，平板尾翼末敏弹难以产生维持末敏弹稳定旋转的转动力矩，故而从末敏弹稳定转速来看，应增大4个弯折角的数值。

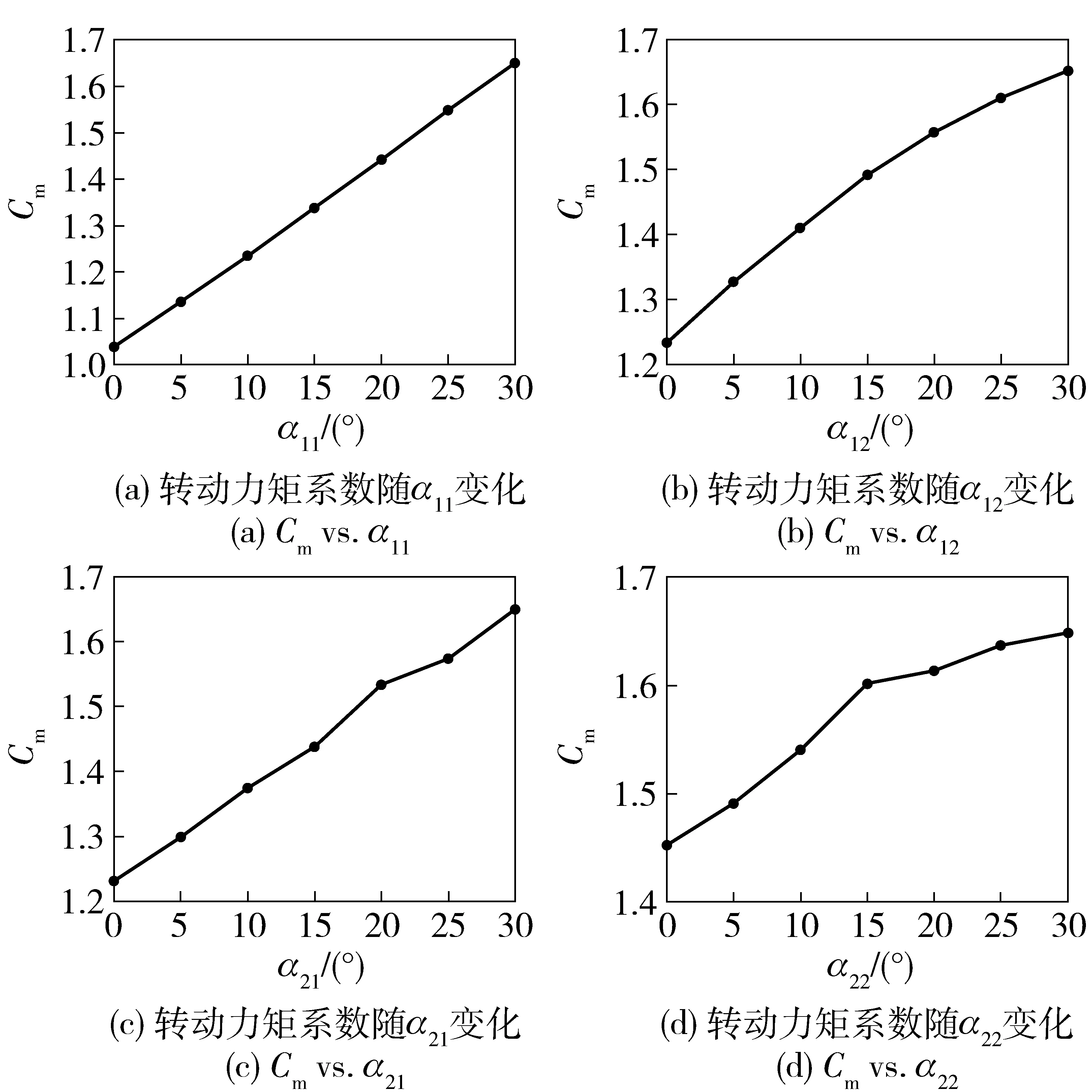
图9 弯折角对转动力矩系数的影响规律Fig.9 Cm vs. bending angle

3.3 弯折比对气动特性的影响

图10所示为尾翼弯折比对S-S型旋翼末敏弹阻力系数的影响规律，可见尽管4条曲线随弯折比的增大或递增或递减，但对比纵轴数据可以看出变化范围很小，各曲线的极差均在2.5%以内，故可认为在本文所取弯折比范围内，此参数不影响旋翼末敏弹的阻力系数。

图10 弯折比对阻力系数的影响规律Fig.10 Cd vs. bending ratio

图11所示为尾翼弯折比对S-S型旋翼末敏弹转动力矩系数的影响规律，可见随4个弯折比的增大，末敏弹转动力矩系数均呈准线性递增趋势，对比4条曲线的斜率，对转动力矩系数影响重要程度的顺序依次是Δ11>Δ21>Δ12>Δ22.

图11 弯折比对转动力矩系数的影响规律Fig.11 Cm vs. bending ratio

图12 长宽比对阻力系数的影响规律Fig.12 Cd vs. length-width ratio

图13 长宽比对转动力矩系数的影响规律Fig.13 Cm vs. length-width ratio

3.4 长宽比对气动特性的影响

图12所示为两翼长宽比对S-S型旋翼末敏弹阻力系数的影响规律，对比纵轴数据可见两曲线的极差很小，均不超过1%，故可认为两翼长宽比不影响末敏弹阻力系数；图13所示为两翼长宽比对S-S型旋翼末敏弹转动力矩系数的影响规律，可见随两翼长宽比的增大，末敏弹转动力矩系数呈递减趋势，对比两曲线斜率，lw1对转动力矩系数的影响略大于lw2.

3.5 尾翼挠曲变形分析

图14所示为S-S型旋翼末敏弹尾翼最大挠曲变形随弯折角的变化规律，可见随弯折角α11的增大，尾翼最大挠曲变形呈递增趋势，在此角度超过15°后变形量保持相对稳定；由其余3个弯折角的纵轴数值来看，尽管变形规律不一，其极差很小，不超过5%，可认为此参数不影响尾翼的挠曲变形。

图14 弯折角对尾翼最大挠曲变形的影响规律Fig.14 Deformation vs. bending angle

图15所示为S-S型旋翼末敏弹尾翼最大挠曲变形随弯折比的变化规律，可见尾翼挠曲变形随Δ11和Δ22的增大呈递增趋势，随Δ12的增大呈递减趋势；图15(c)的纵轴数据显示，Δ21不影响尾翼挠曲变形。

图15 弯折比对尾翼最大挠曲变形的影响规律Fig.15 Deformation vs. bending ratio

图16所示为S-S型旋翼末敏弹尾翼最大挠曲变形随两翼长宽比的变化规律，可见尾翼挠曲变形随lw1的增大呈递减趋势，而lw2对挠曲变形的影响可忽略。

图16 长宽比对尾翼最大挠曲变形的影响规律Fig.16 Deformation vs. l-w ratio

4 试验验证

4.1 样弹模型及场地布置

为验证数值计算的准确性，本文采用高塔自由飞行试验对S-S型旋翼末敏弹进行气动特性测试。加工多枚末敏弹模拟弹，如图17所示。样弹子弹体部分保持直径110 mm和高度135 mm恒定，弹质量4.2 kg，尾翼材料为65Mn弹簧钢，两翼翼展110 mm，厚度为1 mm. 如图18所示，采用高速摄像仪对末敏弹运动姿态进行记录，结合平行于塔身的高度标志物(见图19)对S-S型旋翼末敏弹进行落速及阻力系数分析，而弹体的飞行姿态参数则由弹载姿态记录仪测得。模拟弹自100 m高塔上以人工抛射的方式投出，采用文献[24]所使用的图像处理技术对本文所得数据进行整理。

图17 末敏弹模拟弹Fig.17 TSP model

图18 地面监控站Fig.18 Monitor and camera

图19 高度标记物Fig.19 Height marker

4.2 试验结果分析

自由飞行试验采用8种尾翼结构组合模拟弹，各模型尾翼参数如下：

1)α11=α12=α21=α22=30°,l10=30 mm,l11=l12=80 mm;l20=100 mm,l21=l22=30 mm；

2)α11=α12=α21=α22=30°,l10=100 mm,l11=l12=80 mm;l20=100 mm,l21=l22=30 mm；

3)α11=α12=α21=α22=30°,l10=100 mm,l11=l12=80 mm;l20=130 mm,l21=l22=30 mm；

4)α11=α12=10°,α21=α22=20°,Δ11=Δ12=0.8,Δ21=Δ22=0.15；

5)α11=α12=20°,α21=α22=20°,Δ11=Δ12=0.8,Δ21=Δ22=0.15；

6)α11=α12=20°,α21=α22=30°,Δ11=Δ12=0.8,Δ21=Δ22=0.15；

7)α11=α12=30°,α21=α22=20°,Δ11=Δ12=0.8,Δ21=Δ22=0.15；

8)α11=α12=30°,α21=α22=30°,Δ11=Δ12=0.8,Δ21=Δ22=0.15.

分别对8种不同尾翼结构组合模拟弹进行自由飞行试验，通过弹道参数辨识，可得到各组模型的阻力系数和转动力矩系数。对各模型进行流体- 固体耦合仿真，所得结果如表1所示。

由表1可见，本文所采用的流体- 固体耦合方法求得的旋翼末敏弹气动参数与试验值吻合良好，阻力系数和转动力矩系数的误差分别不超过7.8%和6.1%.

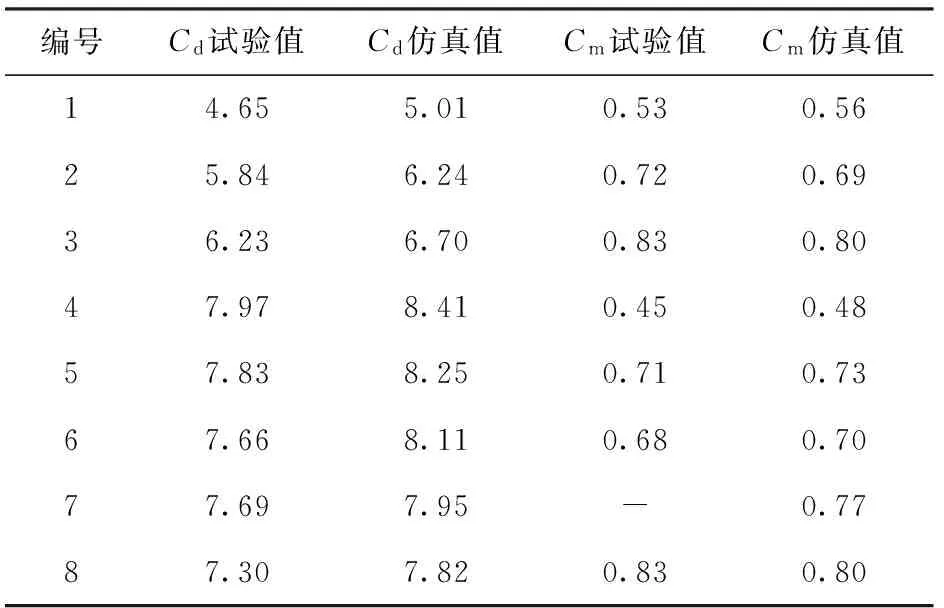
表1 末敏弹模拟弹气动参数试验值与数值解Tab.1 Cd and Cm of TSP

5 结论

本文对S-S型旋翼末敏弹的气动特性进行了仿真及试验分析，深入讨论了尾翼结构参数对旋翼末敏弹气动特性及尾翼变形的影响规律；加工末敏弹模拟弹进行了高塔自由飞行试验，获得其气动参数实测值，通过与仿真结果的对比，得到了以下结论：

1)末敏弹阻力系数随α21的增大呈递增趋势，而随其余3个弯折角的增大呈递减趋势；转动力矩系数随4个弯折角的增大均呈递增趋势。

2)末敏弹转动力矩系数随4个弯折比的增大均呈现准线性递增趋势，对转动力矩系数影响重要程度的顺序依次是Δ11>Δ21>Δ12>Δ22.

3)末敏弹转动力矩系数随两翼长宽比的增大呈递减趋势，且lw1对转动力矩系数的影响略大于lw2.

4)尾翼最大挠曲变形随α11的增大呈递增趋势，在此角度超过15°后变形量保持稳定；随Δ11和Δ22的增大呈递增趋势，随Δ12的增大呈递减趋势；随lw1的增大呈递减趋势。

5)本文所采用流体- 固体耦合方法求得的末敏弹气动参数与试验值吻合良好，阻力系数和转动力矩系数的误差分别不超过7.8%和6.1%，计算方法和结论具有一定的准确性。

References)

[1] 吴太霞, 王婉丽, 刘家英. 国外坦克武器系统精确打击技术现状及发展趋势[J]. 兵工学报, 2010, 31(2):66-69. WU Tai-xia, WANG Wan-li, LIU Jia-ying. Status and trends of precise attack technologies of foreign tank weapon system [J]. Acta Armamentarii, 2010, 31(2):66-69.(in Chinese)

[2] 王国辉, 李向荣, 彭锐枫, 等. 破甲弹对复合装甲毁伤数值模拟分析[J]. 北京理工大学学报:自然科学版, 2014, 34(8):781-785. WANG Guo-hui, LI Xiang-rong, PENG Rui-feng,et al. Numerical simulation on damage effects of shaped charge to composite armor[J]. Journal of Beijing Institute of Technology: Natural Science Edition, 2014, 34(8):781-785.(in Chinese)

[3] 董永忠, 陈廷芬. 高速长杆穿甲弹垂直穿甲过程的实验研究[J]. 兵工学报, 1981, 2(2):36-47. DONG Yong-zhong, CHEN Ting-fen. An experimental research of the vertical penetrating process of the high-velocity long rod armor-piercing projectiles[J]. Acta Armamentarii, 1981, 2(2):36-47.(in Chinese)

[4] 迟润强, Ahmad Serjouei, 范峰, 等. 弹靶尺寸对陶瓷/金属复合装甲防护性能的影响[J]. 爆炸与冲击, 2014, 34(5):594-600. CHI Run-qiang, Ahmad Serjouei, FAN Feng, et al. Geometrical effects on performances of ceramic/metal armors impacted by projectiles[J]. Explosion and Shock Waves, 2014, 34(5):594-600.(in Chinese)

[5] 曹阳, 朱世范, 果春焕, 等. 新型金属间化合物基层状装甲防护复合材料[J]. 兵器材料科学与工程, 2014, 37(6):122-128. CAO Yang, ZHU Shi-fan, GUO Chun-huan,et al. Novel metal-intermetallic laminate composite for armor material[J]. Ordnance Material Science and Engineering, 2014, 37(6):122-128. (in Chinese)

[6] 徐浩铭, 顾文彬, 曾政, 等. 延时起爆对串联EFP成型及其侵彻效应的影响[J]. 高压物理学报, 2014, 28(1): 79-86. XU Hao-ming, GU Wen-bin, ZENG Zheng,et al. Effect of delay time on formation and penetration of tandem EFP[J]. Chinese Journal of High Pressure Physics, 2014, 28(1):79-86.(in Chinese)

[7] 杨绍卿. 灵巧弹药工程[M]. 北京:国防工业出版社, 2010. YANG Shao-qing. Smart munition engineering[M]. Beijing:National Defense Industry Press, 2010.(in Chinese)

[8] Wilkerson S, Hopkins D, Gazonas G, et al. Developing a transient finite element model to simulate the launch environment of the 155-mm SADARM projectile, ADA388168[R]. US: US Army Research Laboratory, 2000.

[9] Nitzche M P. XM898 projectile 155-mm SADARM packaging design and engineering test report, ADA264522[R]. NJ, US: US Army Armament Research, Development and Engineering Center, 1993.

[10] Jameson T C, Luces S A, Knapp D. Comparisons of ballistic trajectory simulations using artillery meteorological messages derived from local balloon data and battlescale forecast model data for the 1998 SADARM IOT & E firings, ADA440117[R]. NM, US: Army Research Lab and Computational & Information Science Directorate US Government, 2001.

[11] Dan B, Paulsson L. Aerodynamics of a rotating body descending from the separation position of an artillery munition shell[C]∥11th Aerodynamic Decelerator Systems Technology Conference. San Diego, CA, US:AIAA, 1991.

[12] 胡志鹏. 双翼末敏弹稳态扫描技术研究[D]. 南京:南京理工大学, 2013. HU Zhi-peng. The study onstable scanning technology of two-wing terminal sensitive projectile[D]. Nanjing:Nanjing University of Science and Technology, 2013.(in Chinese)

[13] Vicente N M, Angel S A, Alvaro C. Experimental investigation of an autorotating-wing aerodynamic decelerator system[C]∥18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Munich, Alemania: AIAA, 2005.

[14] Vicente N M, Angel S A, Alvaro C. Model of the aerodynamic behavior of a pararotor[J]. Journal of Aircraft, 2006, 43(6): 1-15.

[15] Vicente N M, Piechocki J, Cuerva A, et al. Experimental research on a vertically falling rotating wing decelerator model[C]∥19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Williamburg, VA, US:AIAA, 2007.

[16] 舒敬荣, 王代智, 杨海波, 等. 质量分布特性对无伞末敏弹扫描特性的影响规律[J]. 弹道学报, 2015, 27(1):33-39. SHU Jing-rong, WANG Dai-zhi, YANG Hai-bo, et al. Rule of mass distribution characteristics influencing scanning characteristics of non-parachute terminal sensitive ammunition[J]. Journal of Ballistics, 2015, 27(1):33-39.(in Chinese)

[17] 胡志鹏, 刘荣忠, 郭锐. 两种典型尾翼形状对无伞末敏弹气动特性的影响[J]. 南京理工大学学报, 2012, 36(5):739-744. HU Zhi-peng, LIU Rong-zhong, GUO Rui. Effect of two-typical wing shapes on aerodynamic characteristics of non-parachute terminal-sensitive projectile[J]. Journal of Nanjing University of Science and Technology, 2012, 36(5):739-744.(in Chinese)

[18] 郭锐, 刘荣忠, 王本河. 等. 一种非对称双翼结构弹丸减速导旋特性试验研究[J]. 弹箭与制导学报, 2009, 29(5): 249-254. GUO Rui, LIU Rong-zhong, WANG Ben-he, et al. Experimental study on decelerating and spinning characteristics of an asymmetric two-wing projectile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(5):249-254.(in Chinese)

[19] 吕胜涛, 刘荣忠, 郭锐, 等. S-S双翼末敏弹气动外形优化设计[J]. 兵工学报, 2013, 34(9): 1150-1154. LYU Sheng-tao, LIU Rong-zhong, GUO Rui, et al. Optimum design on aerodynamic shape of the S-S style non-parachute terminal sensitive projectile[J]. Acta Armamentarii, 2013, 34(9):1150-1154.(in Chinese)

[20] 周志超, 赵润祥. 不同尾翼灵巧子弹气动特性实验研究[J]. 实验流体力学, 2010, 24(4):52-55. ZHOU Zhi-chao, ZHAO Run-xiang. Experimental investigation on aerodynamic characteristics of smart submunitions with different tail fins[J]. Experiments and Measure in Fluid Mechanics, 2010, 24(4):52-55.(in Chinese)

[21] 舒敬荣, 杨玉林, 张婷, 等. 无伞末敏弹大攻角扫描运动稳定性分析[J]. 航空学报, 2015, 36(10): 3411-3417. SHU Jing-rong, YANG Yu-lin, ZHANG Ting,et al. Analysis on kinetic stability for non-parachute terminal sensitive ammunition’s scanning motion at large angle of attack[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10):3411-3417.(in Chinese)

[22] 张涵信. 关于CFD计算结果的不确定度问题[J]. 空气动力学学报, 2008, 26(1):47-49, 90. ZHANG Han-xin. On the uncertainty about CFD results[J]. Acta Aerodynamica Sinica, 2008, 26(1):47-49, 90.(in Chinese)

[23] 赵博博, 刘荣忠, 郭锐, 等. 新型掠飞末敏弹的捕获概率分析[J]. 兵工学报, 2016, 37(2): 232-238. ZHAO Bo-bo, LIU Rong-zhong, GUO Rui, et al. Research on acquisition probability of a novel hedgehopping terminal sensitive projectile[J]. Acta Armamentarii, 2016, 37(2): 232-238.(in Chinese)

[24] 胡志鹏, 刘荣忠, 郭锐, 等. 基于弹丸图像的末敏弹阻力系数计算方法[J]. 探测与控制学报, 2012, 34(3):8-12, 18. HU Zhi-peng, LIU Rong-zhong, GUO Rui,et al. TSP drag coefficient calculation based on projectile image processing[J]. Journal of Detection & Control, 2012, 34(3):8-12, 18.(in Chinese)

Research on Aerodynamic Characteristics of Terminal Sensitive Projectile with S-S-shaped Flexible Wings

LYU Sheng-tao1, JI Dan-dan1, LIU Rong-zhong2, GUO Rui2, MA Xiao-dong2

(1.School of Chemistry Engineering,Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China; 2.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)

The stabilizing wings are wrapped on the outer wall of terminal sensitive projectile (TSP). The diameter of TSP is generally large to meet the demand of power, which restricts wing thickness. The falling speed of TSP is so quick that the wings deform under the action of aerodynamic force. The effect of the structure parameters of wings on the aerodynamic characteristics of TSP is studied using fluid-structure interaction (FSI) method. The results show that the drag coefficient (Cd) increases withα21and decreases with other bending angles. The moment coefficient (Cm) increases with bending angles and bending ratios,Cmdecreases with length-width ratio of wing. The free flight test results show thatCdandCmare in agreement the simulated results well.

ordnance science and technology; terminal sensitive projectile; aeroelasticity; aerodynamic characteristic; fluid-structure interaction; free flight test

2016-04-05

国家自然科学基金项目(11372136)；国家自然科学基金青年科学基金项目(1102088)

吕胜涛(1985—)，男，博士后。E-mail:st_lv1985@163.com

刘荣忠(1955—)，男，教授，博士生导师。E-mail:liurongz116@163.com

TJ414+.5

A

1000-1093(2017)01-0050-09

10.3969/j.issn.1000-1093.2017.01.007