基于等效磁化强度法的一种电磁式角振动台气隙磁场分析方法

唐波，何闻，贾叔仕

(1.中国计量大学 工业与商贸计量技术研究所, 浙江 杭州 310018；2.浙江大学 机械工程学院 浙江省先进制造技术重点实验室, 浙江 杭州 310027)

基于等效磁化强度法的一种电磁式角振动台气隙磁场分析方法

唐波1,2，何闻2，贾叔仕2

(1.中国计量大学 工业与商贸计量技术研究所, 浙江 杭州 310018；2.浙江大学 机械工程学院 浙江省先进制造技术重点实验室, 浙江 杭州 310027)

针对有限元法求解气隙磁场的磁路几何模型占用内存空间多和计算时间长等问题，提出一种基于等效磁化强度法求解电磁式角振动台气隙磁场分析方法。基于等效磁化强度法建立矢量磁位的微分方程组，得到包含磁路几何参数的磁感应强度解析表达式；与有限元法计算结果对比，验证等效磁化强度法的正确性；采用等效磁化强度法对磁路参数进行优化。分析结果表明：当气隙厚度保持不变时，随着永磁体扇形角的增加，气隙中有效均匀磁感应强度的区域变宽，而随永磁体厚度的增加，气隙磁感应强度将增强；当永磁体扇形角和厚度保持不变时，磁感应强度随气隙厚度的增加而减小。该方法可以快速分析磁路结构参数变化对气隙磁感应强度的影响程度，为优化设计电磁式角振动台磁路结构提供理论参考。

电磁学；角振动台；气隙磁场；等效磁化强度法；有限元法

0 引言

随着科学技术的发展，角振动传感器在航空航天、交通运输和工业自动化等领域得到广泛应用[1-2]。同线振动传感器类似，为实现角振动传感器测量结果的准确性和统一性，出厂或使用一段时间后需要对其进行校准[3-4]。电磁式角振动台是用于校准角振动传感器的角运动发生设备，其性能将影响角振动传感器的校准精度，而磁路结构设计是电磁式角振动台的重要环节[5]。基于轴向气隙磁场的磁路结构具有能量转换效率高、气隙磁感应强度大和结构紧凑等优点[6-7]，提出了一种适用于电磁式角振动台的双磁源磁路，对其磁路参数进一步优化设计，改善气隙磁场分布特性，对设计优良特性的电磁式角振动台具有重要的意义。

对于普通磁路结构分析，一般采用有限元法[8]和解析法[9]。有限元法虽然求解准确、精度高，但前处理复杂、求解时间长，无法直接反映出某参数变化对气隙磁场的影响，而解析法具有简洁、快速的特点，其关键还在于通过建立的解析表达式，可直接研究磁路结构参数对气隙磁场特性的影响。解析法主要有等效磁路法[10]和等效磁化强度法[11-12]，等效磁路法存在精确建模困难，漏磁系数和磁阻系数采用经验值，对于不同磁路结构其取值大小不同等问题；等效磁化强度法是将永磁体等效成磁化强度，将整个求解区域划分成：气隙区域和永磁体区域，从而建立矢量磁位的微分方程组，该方法具有解析公式简单、求解精度高的特点[13-14]。本文采用等效磁化强度法推导了电磁式角振动台双磁源磁路的气隙磁感应强度解析公式，并通过有限元法验证该解析公式的正确性。最后采用等效磁化强度法对磁路参数进行优化。

1 双磁源磁路结构

具有双磁源磁路结构的电磁式角振动台结构模型如图1所示，主要由运动部件、空气轴承、弹性装置和双磁源磁路等组成。运动部件的上端部为角振动台台面，用于安装被校准角振动传感器，下端部连接圆盘式动圈，为动力发生部；运动部件通过空气轴承气浮支撑，以减小运动摩擦力，提高运动精度；弹性装置用于保持运动部件的平衡位置。

图1 角振动台结构模型Fig.1 Structural model of angular vibrator

角振动台的动力源是位于双磁源磁路结构气隙磁场中圆盘式动圈受到的力矩作用，原理图如图2所示。图2中表示了单匝线圈在磁场中受力的情形：两个独立的单匝线圈在相邻处沿圆盘径向位置形成两个驱动力部，分别位于两段磁场区域中，且两段磁场的磁感应强度B1(方向朝下)和B2(方向朝上)的方向均垂直于圆盘式动圈平面；合理设计线圈的绕向，使得当导线通过电流时，处于两段磁场中的导线将因受洛伦兹力的作用而同时产生顺时针或逆时针的扭转力矩，从而推动运动部件产生旋转运动。

图2 圆盘式动圈产生力矩Fig.2 Generation of force moment on disk moving coil

为了提高机电转换效率及输出波形精度，实现强而均匀的气隙磁场是关键。所谓双磁源磁路结构由上下永磁体、上下导磁体、导磁环及气隙构成，如图3所示。根据串联式磁路结构特性，当上、下对应永磁体的磁化方向相同时，可有效增强气隙磁感应强度。根据圆盘式动圈导线由内绕到外或由外绕到内的方式，同一根导线形成的两个驱动力部的导线中电流方向相反，因此对应永磁体处的磁场方向相反，从而在驱动力部处产生相同方向的旋转力矩，使角振动台输出旋转加速度。

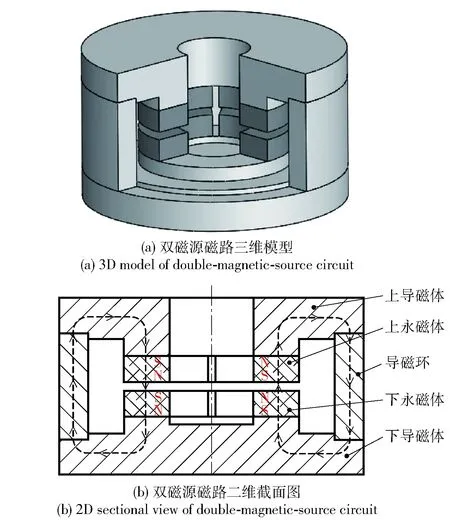
图3 磁路结构Fig.3 Magnetic circuit structure

2 等效磁化强度法

等效磁化强度法首先将三维模型等效为二维模型，接着采用永磁体的等效磁化强度分布函数建立矢量磁位的微分方程组，然后用分离变量法求解方程，最后得到包含磁路参数的气隙区域磁感应强度解析表达式。

以永磁体平均半径围成的曲面为基准，将其展开成平面，则双磁源磁路三维模型转化成二维等效磁路模型，并做以下假设：1)导磁体的磁导率为无穷大；2)展开后的双磁源磁路结构上下对应的永磁体沿着展开方向周期性复现；3) 永磁体的径向方向尺寸假设为无限大。利用对称性简化求解过程，以气隙中心线为x轴，以永磁体分布对称线为y轴建立直角笛卡尔坐标系，展开后的等效双磁源磁路模型如图4所示，图中将求解区域划分为3个区域：气隙区域Ⅰ、下永磁体区域Ⅱ和上永磁体区域Ⅲ.

图4 等效双磁源磁路模型Fig.4 Model of equivalent double-magnetic-source magnetic circuit

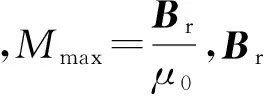
图5 下永磁体磁化强度分布Fig.5 Distribution of lower permanent magnet magnetization intensity

根据图5磁化强度分布规律，可得永磁体磁化强度分布函数M(x)的傅立叶级数[15]为

(1)

在气隙区域Ⅰ中，矢量磁位AzI满足拉普拉斯方程

(2)

在永磁体区域Ⅱ和Ⅲ中，矢量磁位AzII和AzIII分别满足泊松方程

(3)

式中：M(x)=MII(x)=-MIII(x)，MII(x)为下永磁体的磁化强度分布，MIII(x)为上永磁体的磁化强度分布。

气隙区域Ⅰ和永磁体区域Ⅱ、Ⅲ中偏微分方程的通解可表示为

(4)

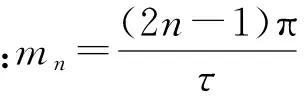
由于气隙区域Ⅰ和永磁体区域Ⅱ、Ⅲ关于x轴对称，则

(5)

根据磁通折射定律，磁通在通过交界面时磁场强度的切向分量连续，而磁感应强度的法向分量连续，由此可以得到不同区域的边界条件。

气隙区域Ⅰ和下永磁体区域Ⅱ交界面上的边界条件为

(6)

式中：HxI(x,y)和HxII(x,y)分别为气隙区域I和下永磁体区域Ⅱ切向分量的磁场强度；ByI(x,y)和ByII(x,y)分别为气隙区域I和下永磁体区域Ⅱ法向分量的磁感应强度。

气隙区域Ⅰ和上永磁体区域Ⅲ交界面上的边界条件为

(7)

式中：HxIII(x,y)为上永磁体区域Ⅲ切向分量的磁场强度；ByIII(x,y)为上永磁体区域Ⅲ法向分量的磁感应强度。

由于假设导磁体的磁导率为无穷大，下永磁体区域Ⅱ和上永磁体区域Ⅲ与导磁体界面上磁感应强度切向分量为0，则磁感应强度的边界条件为

(8)

将(5)式、(6)式、(7)式和(8)式代入(4)式中，并化简得

(9)

通过(9)式对矢量磁位求偏导，得到气隙区域中的磁感应强度ByI法向分量的表达式为

(10)

从(10)式中可以看出，气隙磁感应强度与永磁体剩余磁感应强度Br、永磁体宽度τm、永磁体所占极距τ、永磁体厚度hm和气隙厚度h有关。

3 气隙磁场分析

由于角振动台的双磁源磁路中采用相同的永磁体，除永磁体的磁化方向有区别外，其他磁性能均保持一致，另外又由于磁路结构的对称性，形成的闭合磁回路路径也相同，因此每条闭合磁回路气隙磁感应强度大小相等，方向相同或相反。鉴于此，可取其中一条闭合磁回路分析气隙磁场的分布特性。上、下永磁体正对着的气隙为扇形气隙磁场，以扇形气隙磁场平均半径处的圆弧为测试路径，圆弧起点、终点与原点之间连线形成的夹角为扇形气隙角度。

3.1 等效磁化强度法的解

借助Matlab商用数值分析软件，对气隙区域磁感应强度解析表达式(10)式进行有限阶次展开，得到不同阶数时气隙磁感应强度分布的解，如图6所示。

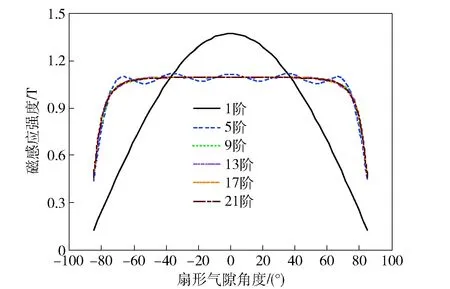
图6 气隙磁感应强度分布Fig.6 Distribution of MFDs in air-gap

由图6可见，当展开阶数大于13阶后，曲线基本重叠，从而说明表达式的解收敛；进一步，以展开阶数21阶作为参考值，计算各展开阶数下解的误差收敛情况，如图7所示。由图7可见，随着表达式展开阶数的增加，气隙磁感应强度分布解的误差逐渐减小，分布曲线变得光滑和平坦。气隙磁感应强度分布曲线呈两端部小、中间大而均匀的趋势，这是由于永磁体的边缘效应引起，越靠近端部漏磁越多，磁阻也越大。

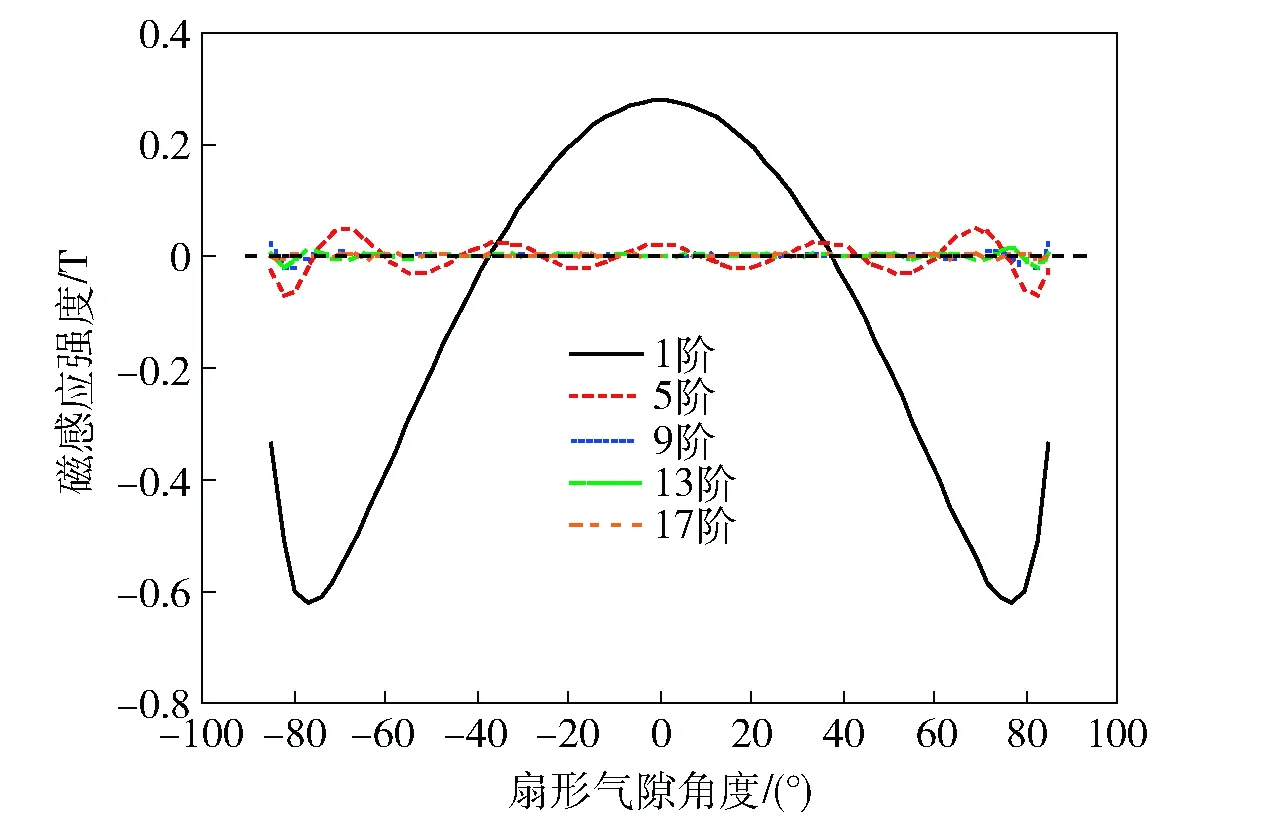
图7 气隙磁感应强度分布解的误差分析Fig.7 Error analysis of distributed solution for air-gap MFDs

3.2 等效磁化强度法解的验证

有限元是准确计算电磁场的有效工具，在磁路结构和参数确定后进行精确分析具有独特的优势，因此采用有限元法对等效磁化强度法求解气隙磁感应强度分布结果的正确性进行验证。考虑到求解结果的可比性，根据相同磁路几何模型和参数，采用基于磁化强度法和有限元法对永磁体扇形气隙角度为170°时的气隙磁感应强度分布情况进行比较，其结果如图8所示。

图8 两种方法气隙磁感应强度分布Fig.8 Distribution of MFDs with two methods

从图8中可以看出，采用等效磁化强度法与有限元法求得的气隙磁感应强度分布曲线基本一致，验证了等效磁化强度法的正确性，中间段上等效磁化强度法求得的值大于有限元法是由于等磁化强度法计算时未考虑导磁体的磁阻而有限元法分析时考虑了导磁体的磁阻。

3.3 磁路参数对气隙磁场的影响

3.3.1 永磁体扇形角的影响

由图2的圆盘式动圈驱动原理可知，为了使得在驱动力部产生同向的驱动力矩，必须在两个驱动力部处有两个方向相反的气隙磁场，所以双磁源磁路中上、下永磁体必须分别由两块极性相反的磁体拼接起来，其中每块磁体的扇形角大小对气隙磁场的影响有必要进行计算研究。在永磁体厚度和气隙厚度不变的条件下，选取永磁体的扇形角分别为160°、170°和175° 3种情况，计算得到气隙磁感应强度分布如图9所示。

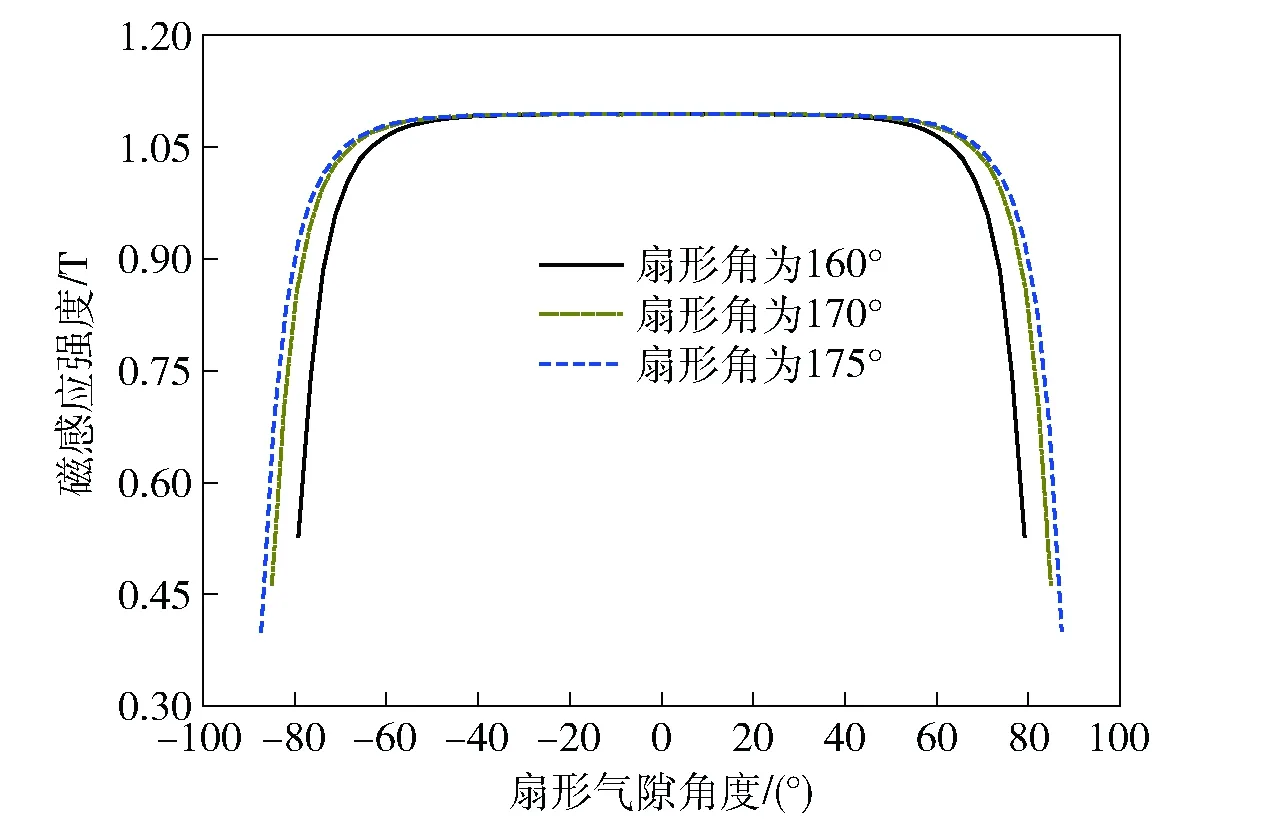
图9 不同永磁体扇形角时气隙磁感应强度分布Fig.9 Distribution of air-gap MFDs at different sector angles of PM

从图9中可以看出，随着永磁体扇形角的增大，气隙中有效均匀磁感应强度的区域越宽；然而扇形角过大，相邻永磁体之间的漏磁作用增强，影响气隙磁感应强度分布，同时也不利于永磁体的安装和固定。因此在选取永磁体扇形角度时既要考虑动圈的有效运动范围，又要考虑永磁体的安装问题，二者之间需要合理取舍。

3.3.2 永磁体厚度的影响

由于角振动台双磁路的磁源为永磁体，永磁体厚度涉及到永磁体内部磁能大小，直接影响到气隙磁感应强度的大小，从而影响圆盘式动圈输出力矩能力，在永磁体扇形角和气隙厚度不变的条件下，对永磁体厚度为13 mm、17 mm和21 mm 3种情况的气隙磁感应强度分布进行分析，其计算结果如图10所示。

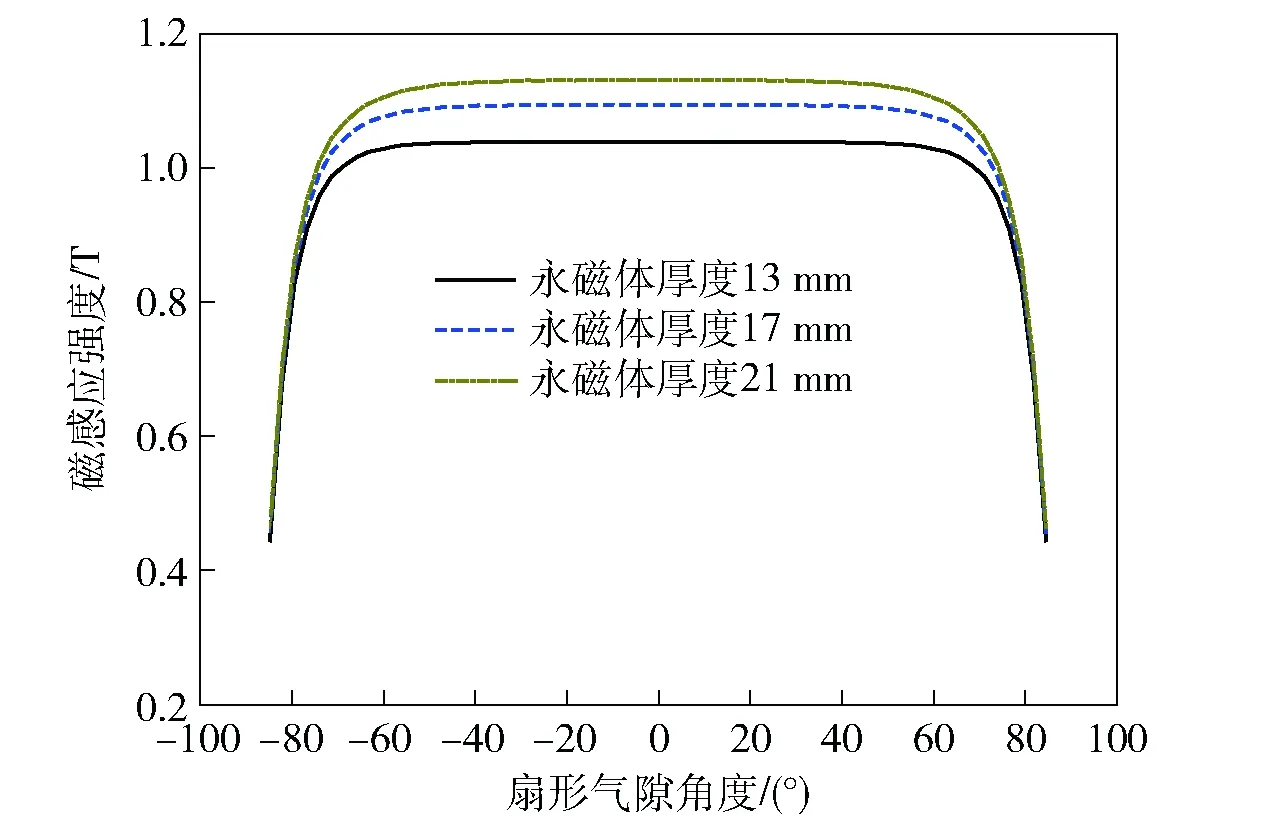
图10 不同永磁体厚度时气隙磁感应强度分布Fig.10 Distribution of air-gap MFDs for different thickness of PM

从图10中可以看出，随着永磁体厚度的增加，气隙磁感应强度也随之增加，增加幅值先大后小，但是由于永磁体的磁导率接近于空气，永磁体厚度增加的同时也增加了磁阻，由于磁阻的非线性，由此造成永磁体厚度的增加量与气隙磁感应强度的增加量不呈正比关系。

3.3.3 气隙厚度的影响

气隙磁场是电磁式角振动台实现机电能量转换的重要载体，在扇形角和永磁体厚度不变的条件下，分别对气隙厚度为5 mm、7 mm和9 mm 3种情况的气隙磁感应强度分布进行分析，其结果如图11所示。

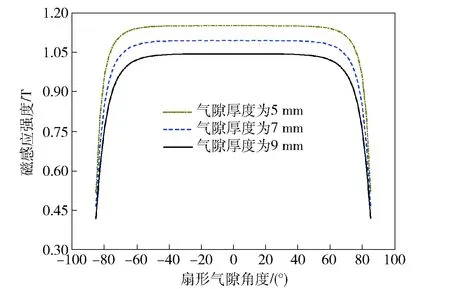
图11 不同气隙厚度时气隙磁感应强度分布Fig.11 Distribution of air-gap MFDs for different thicknesses of air-gap

从图11中可以看出，在磁路结构确定的条件下，气隙厚度越小，气隙磁感应强度越大，气隙磁感应强度大是由于气隙磁场中单位体积的能量密度增大引起。为了获得强的气隙磁感应强度，在满足条件的情况下，气隙厚度越小越好，然而气隙的厚度受到圆盘式动圈厚度的限制。

4 实验验证

将优化后的双磁源磁路参数应用于电磁式角振动台样机中，同时为了测试电磁式角振动台样机中气隙磁场的分布特性，采用BST-100高斯计对气隙磁场的磁感应强度进行测试，在气隙磁场平均半径位置上沿圆周方向每隔10°作为一个测试点，实测得到的气隙磁感应强度分布如图12所示。

图12 电磁式角振动台气隙磁感应强度分布Fig.12 Distribution of air-gap MFDs in the electromagnetic angular vibrator

通过图12中测试值和计算值对比可以看出，二者具有类似的分布趋势，由于机械间隙、实际的永磁体性能参数和物理尺寸存在偏差，测试得到的磁感应强度稍低于理论计算值，验证了解析算法的正确性。

5 结论

本文提出一种基于等效磁化强度法求解电磁式角振动台双磁源磁路气隙磁感应强度的分析方法，采用变量分离法求解气隙区域拉普拉斯方程和永磁体区域泊松方程，得到包含磁路几何参数的气隙区域磁感应强度的解析表达式，借助Matlab商用数值分析软件对气隙磁感应强度的分布情况进行数值求解，并与有限元法求得的结果进行对比，二者的磁感应强度分布趋势一致，验证了等效磁化强度法的正确性。通过等效磁化强度法计算，结果表明：当气隙厚度保持不变时，随着永磁体扇形角的增加，气隙中有效均匀磁感应强度的区域变宽，而随永磁体厚度的增加，气隙磁感应强度将增强；当永磁铁扇形角和厚度保持不变时，磁感应强度随气隙厚度的增加而减小。该方法可以快速分析磁路结构参数变化对气隙磁感应强度的影响程度，为优化设计电磁式角振动台磁路结构提供理论参考。

References)

[1] Naqui J, Martin F. Transmission lines loaded with bisymmetric resonators and their application to angular displacement and velocity sensors[J]. IEEE Transactions on Microwave Theory and Techniques, 2013, 61(12): 4700-4713.

[2] Mustafa M S, Cheng P, Oelmann B. Stator-free low angular speed sensor based on a MEMS gyroscope[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(11): 2591-2598.

[3] ISO 16063—2006 Methods for calibration of vibration and shock transducers [S]. Geneva: ISO Copyright Office, 2006.

[4] GB/T 20485—2010 振动与冲击传感器校准方法[S]. 北京:中国标准出版社, 2010. GB/T 20485—2010 Methods for calibration of vibration and shock transducers [S]. Beijing: Standards Press of China, 2010. (in Chinese)

[5] 唐波, 何闻. 宽频带电磁式角振动台运动部件动态优化设计[J]. 农业机械学报, 2015, 46(10): 376-382, 390.

TANG Bo, HE Wen. Dynamic optimization design of moving component for broadband electromagnetic angular vibration[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(10): 376-382, 390. (in Chinese)

[6] Park S, Kim W, Kim S. A numerical prediction model for vibration and noise of axial flux motors[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10):5757-5762.

[7] Pippuri J, Manninen A, Keranen J, et al. Torque density of radial, axial and transverse flux permanent magnet machine topologies[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2339-2342.

[8] 刘晓, 叶云岳, 郑灼, 等. 永磁直线伺服电机的磁场分析及优化设计[J]. 浙江大学学报:工学版, 2008, 42(11): 1962-1965. LIU Xiao, YE Yun-yue, ZHENG Zhuo, et al. Magnetic analysis and optimization of permanent magnet linear servo motor[J]. Journal of Zhejiang University:Engineering Science, 2008, 42(11):1962-1965. (in Chinese)

[9] He W, Wang C Y, Yu Mei, et al. Closed-double-magnetic circuit for a long-stroke horizontal electromagnetic vibration exciter[J]. IEEE Transactions on Magnetics, 2013, 49(8):4865-4872.

[10] 赵精晶, 石庚辰, 杜琳. 盘式永磁微型发电机的磁路设计方法[J]. 兵工学报, 2014, 35(8): 1144-1151. ZHAO Jing-jing, SHI Geng-chen, DU Lin. Design method of magnetic circuit in planar permanent magnetic micro-generator[J]. Acta Armamentarii, 2014, 35(8): 1144-1151.(in Chinese)

[11] Wang J B, Jewell G W, Howe D. A general framework for the analysis and design[J]. IEEE Transactions on Magnetics, 1999, 35(3):1986-1999.

[12] Kang G H, Hong J P, Kim G T. A novel design of an air-core type permanent magnet linear brushless motor by space harmonics field analysis[J]. IEEE Transactions on Magnetics, 2001, 37(5): 3732-3736.

[13] 刘晓, 叶云岳, 郑灼, 等. 空心式永磁直线伺服电机气隙磁场及推力分析[J]. 浙江大学学报:工学版, 2010，44(3):533-538. LIU Xiao, YE Yun-yue, ZHENG Zhuo, et al. Magnetic field and thrust analysis of air-cored permanent linear servo motor[J]. Journal of Zhejiang University:Engineering Science, 2010, 44(3): 533-538. (in Chinese)

[14] 葛研军, 聂重阳, 辛强. 调制式永磁齿轮气隙磁场及转矩分析计算[J]. 机械工程学报, 2012, 48(11):153-158. GE Yan-jun, NIE Chong-yang, XIN Qiang. Analytical calculation of air-gap magnetic field and torque of modulated permanent magnetic gears[J]. Journal of Mechanical Engineering, 2012, 48(11):153-158.(in Chinese)

[15] 叶其孝, 沈永欢. 实用数学手册[M]. 第2版. 北京:科学出版社, 2006. YE Qi-xiao, SHEN Yong-huan. Practical mathematics handbook[M]. 2nd ed. Beijing: Science Press, 2006. (in Chinese)

An Air-gap Magnetic Field Analysis Method of Electromagnetic Angular Vibrators Based on Equivalent Magnetization Intensity Method

TANG Bo1,2，HE Wen2，JIA Shu-shi2

(1.Institute of Industry and Trade Measurement Technique, China Jiliang University, Hangzhou 310018, Zhejiang, China;2.Key Laboratory of Advanced Manufacturing Technology of Zhejiang Province, College of Mechanical Engineering, Zhejiang University, Hangzhou 310027, Zhejiang, China)

The finite element method (FEM) takes much more memory space and computing time for establishing a magnetic circuit geometrical model for the analysis of the air-gap magnetic field . An efficient analytical approach is presented to solve the air-gap magnetic field of electromagnetic angular vibrators based on the equivalent magnetization intensity method (EMIM). The differential equations of the magnetic potential vector are built up based on the EMIM, and an analytical expression of magnetic flux density (MFD) that contains the geometrical parameters of magnetic circuit is derived. The effectiveness of EMIM is verified by comparing the calculated results of FEM and EMIM. The magnetic circuit parameters are optimized by using EMIM. The results show that the region of the effective uniform MFD is widened with the increase in the sector angle of permanent magnet (PM), and MFD in the air-gap becomes strong with the increase in the thickness of PM when the thickness of air-gap remains constant. MFD decreases with the increase in the thickness of air-gap when the sector angle and thickness of PM remain constant. The proposed method can be used to quickly analyze the parameters of magnetic circuit that impact on the air-gap magnetic field, and provide the theoretical reference of the magnetic circuit optimal design in electromagnetic angular ribrators.

electromagnetism；angular vibrator；air-gap magnetic field；equivalent magnetization intensity method；finite element method

2016-04-06

国家自然科学基金项目(51375443)；国家重大仪器设备开发专项项目(2013YQ470765)；浙江省自然科学基金杰出青年基金项目(LR12E05001)；浙江省先进制造技术重点实验室开放基金项目(2016KF05)

唐波(1985—)，男，讲师。E-mail:tang-bo001@163.com

何闻(1969—)，男，教授，博士生导师。E-mail:hewens@zju.edu.cn

TB534+.2

A

1000-1093(2017)01-0202-07

10.3969/j.issn.1000-1093.2017.01.027