三叶孔板强化换热性能及机理分析
魏志国,李华峰,柯汉兵,张克龙
(武汉第二船舶设计研究所热能动力技术重点实验室,湖北 武汉 430205)
三叶孔板强化换热性能及机理分析
魏志国,李华峰,柯汉兵,张克龙
(武汉第二船舶设计研究所热能动力技术重点实验室,湖北 武汉 430205)
三叶孔板是以纵向流形式强化管壳式换热器性能的一种典型支撑板结构,具有附加阻力小和能够降低管束流激振动等诸多优势。为了分析三叶孔板对管壳式换热器壳程传热性能的强化效果和机理,本文依据周期性和对称性特征构建了不同孔高的换热器单元流道模型,采用重整化群k-ε湍流模型和SIMPLE耦合算法分析其壳程流场分布特征并评估其综合换热性能。结果表明,三叶孔板换热器Nu数和阻力系数较无孔板管壳式换热器均有所增加,相对Nu数(Nu/Nu0)和相对阻力系数(f/f0)随孔高H增大而减小,性能评价指标(performance evaluation indicators,PEC)随孔高H增大而增大。与无孔板管壳式换热器相比,三叶孔板换热器壳程纵向各处场协同角β较小而纵向涡强度Ωx较大,因此场协同性的改善和纵向涡强度的提高是三叶孔板强化换热的原因。
三叶孔板;强化换热;综合性能;机理分析
管壳换热器是重要的间壁式换热器类型[1]。为提高其传热能力,通常采用弓形、环形等各类折流板使壳程流体产生宏观横向运动、增大其冲刷管壁流速,从而达到提高壳程以及总传热系数的目的,但由此也带来了换热器阻力加大、管束诱导振动等问题,对综合效能和可靠性产生负面影响。
为了解决上述问题,相关学者提出了螺旋折流板等新型管壳式换热器折流板形式,以之代替弓形、环形折流板不仅可以降低换热器壳程流阻、弱化管束激振,而且能够较好地避免由结垢、漏流等引起的传热性能恶化现象[2],螺旋折流板换热器的以上种种优点使其在诸多领域展现出广阔应用前景。
采用三叶孔板等纵流换热器取代横流换热器是解决上述问题的另一种途径,虽然此类换热器对于水-水等低黏度介质的强化换热作用不及螺旋折流板换热器,但是在降低流动阻力[3]以及管束振动抑制[4]方面表现出一定的自身优势,并且通过特征结构的优化设计同样可以获得较好的综合换热性能,因此三叶孔板换热器在船舶动力以及核电等对于泵功率、结构振动和可靠性具有特殊要求的行业领域具有潜在应用价值。鉴于目前有关三叶孔板换热器强化换热机理的研究较为欠缺,本文借助通用CFD软件平台开展其换热特性仿真分析并阐释其强化换热机理,以期为三叶孔板换热器的结构优化改进提供理论指导。
1 计算方法
1.1 几何结构及网格剖分
三叶孔板换热器的主要换热功能部件包括三叶支撑孔板和换热管,相邻孔板由纵向管支撑定距,由于三叶孔板主要改变的是壳程流动,可针对壳侧流场进行单向换热分析,其典型横截面结构及特征尺寸如图1所示。其中,S为相邻换热管的管间距,Ro为换热管外半径,H为三叶孔的开孔高度。
从图1可以看出,三叶孔板换热器壳程结构具有明显的周期性和对称性,据此可以对换热器结构模型进行简化。本文针对换热管和三叶孔板对称面围成区间建立了壳程的单元流道模型[5]。在此基础上,对上述计算域进行了空间结构离散,典型三叶孔板换热器单元流道模型结构和网格剖分情况如图2所示。
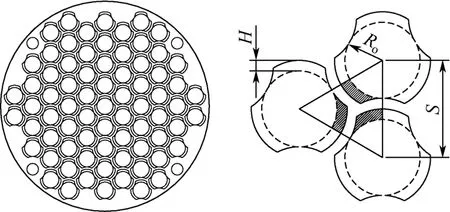
图1 三叶孔板换热器模型结构及特征尺寸
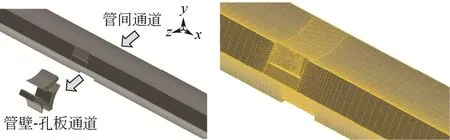
图2 三叶孔板换热器单元流道模型结构及网格
考虑到开孔高度是换热器综合性能的主要影响因素之一[6],因此在建模过程中通过调整三叶孔板间隙高度改变换热器结构,以分析其对于强化换热的影响规律(模型特征结构参数见表1)。与此同时,在管间距、管径、布管方式相同的条件下创建了无孔板单元流道模型CASE-0,作为分析对照基准。表1给出了不同流道模型的特征结构尺寸参数,其中各模型中三叶孔板厚度均为5mm,间距300mm。

表1 三叶孔板换热单元模型及几何参数
1.2 数值离散方法及边界条件
在三叶孔板换热器性能分析过程中采取了以下简化假定:
(1)壳侧换热流体为不可压缩流体(水),由于温度区间较小物性参数恒定,其流动换热为定常过程;
(2)忽略重力和由于流体密度差异引起的浮升力;
(3)忽略由于黏性耗散引起的热效应;
(4)所有界面和接触表面不变形,液固接触面无滑移。
在上述假定条件下,三叶孔板换热器壳程流道的流动换热过程遵循的连续性方程、动量方程、能量方程等控制方程的通用格式为式(1)[7]。
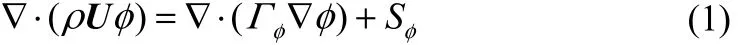
湍流模型选用RNGk-ε模型[8],以提高对三叶孔板换热器壳测流场畸变的计算精度。数值计算过程中压力-速度耦合采用SIMPLE算法,压力项的差分采用标准差分格式,其他项的差分采用Second Order Upwind格式。连续性方程、动量方程、k方程和ε方程收敛残差均为10−6级,能量方程的收敛残差设置为10−8级。
各个几何边界的边界条件设定如图3所示。
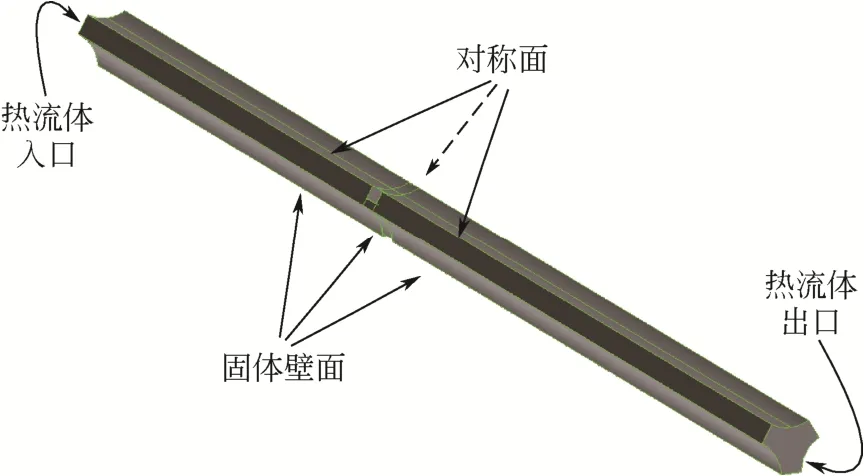
图3 三叶孔板换热器单元流道仿真模型边界条件
(1)壳程热流体入口为速度入口条件。其中速度大小uin;方向垂直于入口截面;入口温度Tin;湍流强度,其中,水力直径。
(2)壳程热流体出口为压力出口条件,出口压力均匀恒定。
(3)换热器管壁和支撑孔板为无滑移固体壁面,其中前者为等温条件,壁温Tw,后者为绝热条件。贴壁湍流黏性底层采用标准壁面函数法进行处理。
(4)相邻换热基本单元的共用界面为对称边界。
另外需要说明的是,为了避免入口效应影响,根据xfd,t/De≥10设置了入口长度,保证换热过程的充分发展[9]。
1.3 网格无关性考核
为了得到三叶孔板换热器传热特性的网格独立解,以CASE-3为例在表2所列边界条件下对不同网格节点数的离散模型进行了仿真计算。
图4给出了不同网格数量下换热器单元流道的压差、传热性能曲线。结果表明,在网格单元尺寸小于0.08mm、数量超过390万以后,换热通道阻力以及传热系数随网格数量的增加相对变化较小。由于结构变化不大,其他模型的网格无关性考核结果与之类似,后续分析模型的网格划分密度均以此为准。
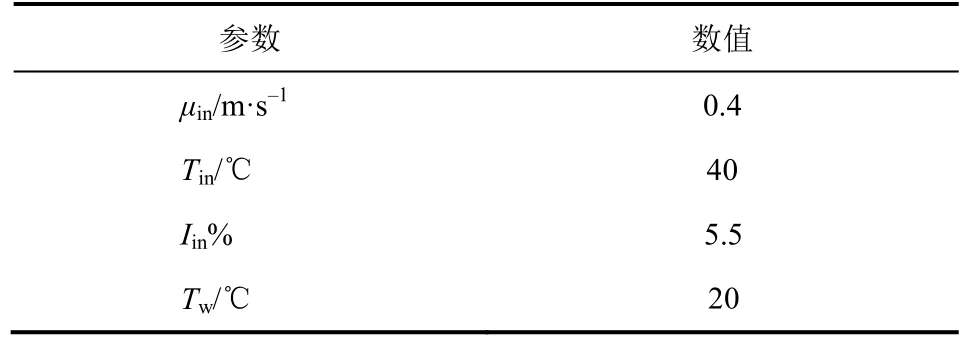
表2 网格无关性考核主要边界条件
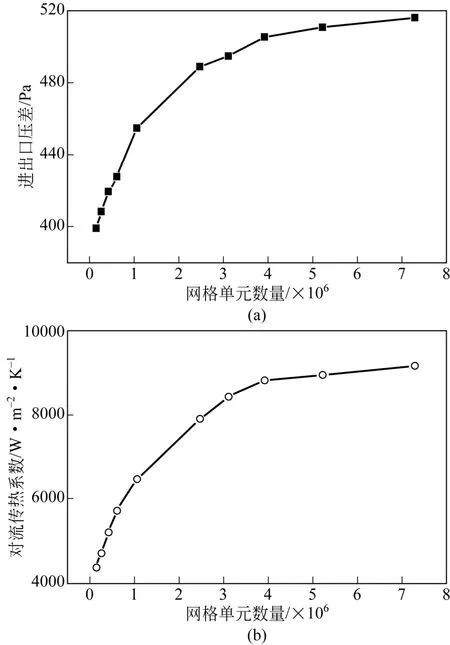
图4 典型三叶孔板换热单元网格独立性考核
1.4 数值计算方法验证
采用上述方法,在Re=1×104~1.5×104范围内对三叶孔板换热器的传热性能进行了计算分析,并将数值仿真与试验结果[10]进行了对比,以验证本文计算方法的准确性,对比结果如图5所示。从对比情况来看,基于单元流道模型的换热器传热性能数值计算结果与试验结果具有较好的一致性,相对误差在3%以内,可以满足换热器性能分析的精度要求。
2 三叶孔板强化换热性能分析
为了分析三叶孔板对换热器壳侧对流传热的强化效果,首先在单元流道模型孔板后沿纵向等间隔截取分析平面如图6所示(对无孔板管壳换热器也在对应位置截取分析平面),进而采取面积平均方法对壳程状态参数分布进行纵向一维简化。
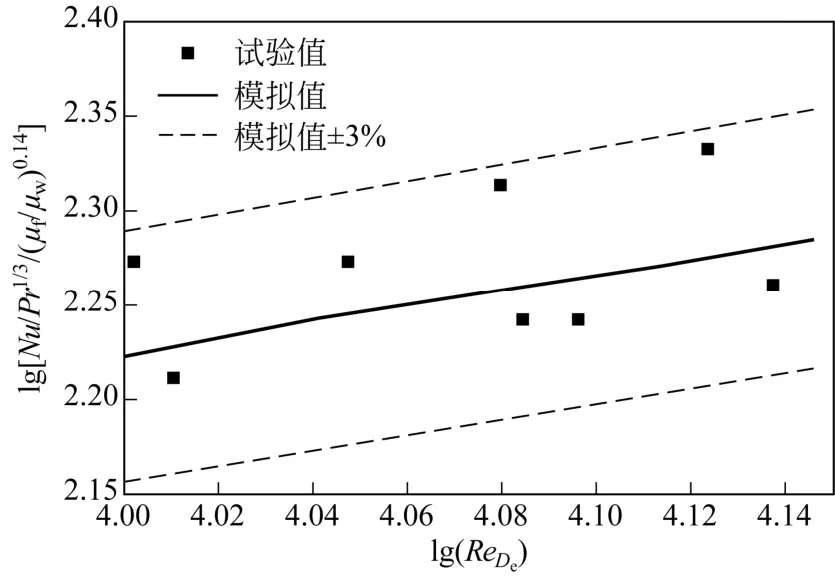
图5 数值计算方法验证结果
图7对比了相同条件下不同孔高的三叶孔板换热器以及无孔板换热器壳侧温度的纵向分布。结果表明,三叶孔板换热器纵向各点的平均温度均明显低于无孔板管壳式换热器,且两种换热器的壳程截面平均温差随流动的发展而逐渐增大,由此可知三叶孔板在板后相当长距离内对壳程对流换热均有强化效果,存在累积效应。


图6 三叶孔板换热器单元流道模型分析截面
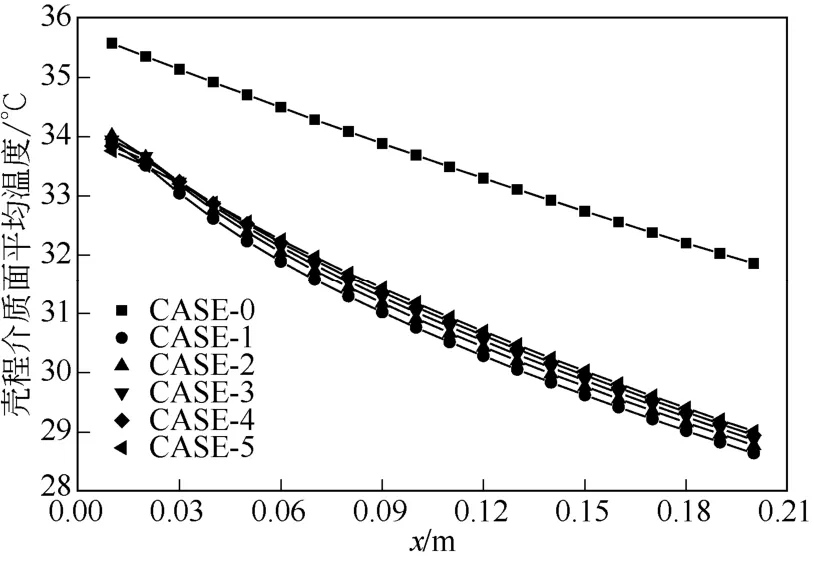
图7 换热器单元流道纵向温度分布对比曲线

以无孔板管壳换热器为基准,分别计算了不同孔高H条件下三叶孔板换热器的相对Nu数以及相对阻力系数如图8所示。结果表明,三叶孔板换热器相对Nu数随H增大而降低,说明孔高越小壳程对流换热能力越强;另一方面,相对阻力系数也随H的增加而降低,说明孔高越小壳程流动阻力越大为了较为全面反映三叶孔板对管壳式换热器换热和阻力性能的影响,采用性能评价指标PEC对换热器进行综合评价,见式(4)[11]。

不同孔高条件下三叶孔板换热器单元流道的PEC计算结果如图9所示,从中可以看出,在本文分析区间内三叶孔板换热器PEC随孔高H的增加而增大,且在H≥2mm情况下有PEC>1,说明当间隙高度大于上述临界值时三叶孔板对壳程对流换热性能的强化作用才能充分抵消流动阻力增加对换热综合性能产生的负面影响。
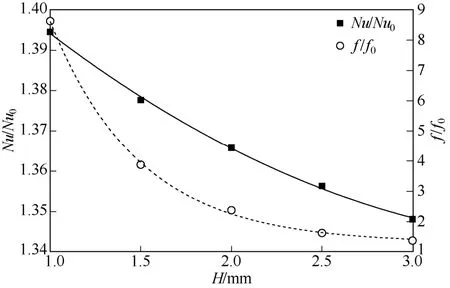
图8 三叶孔板换热器相对Nu数和阻力系数
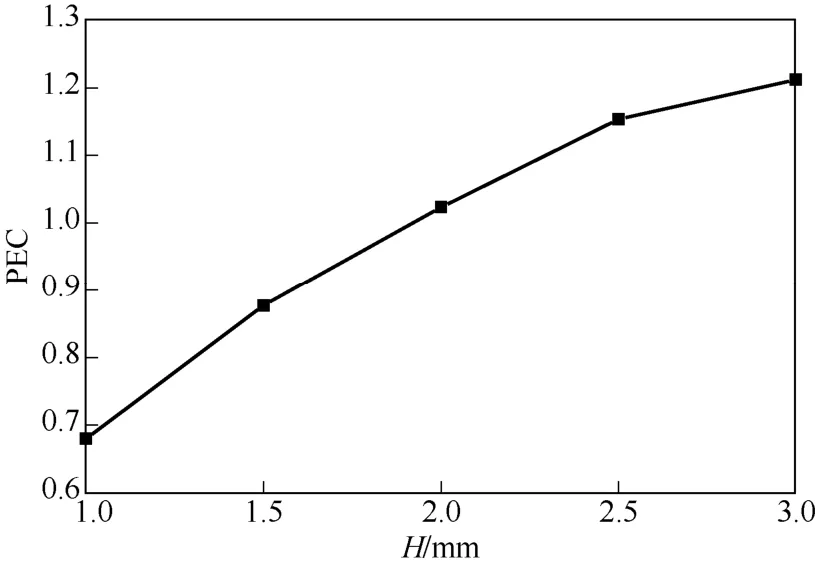
图9 三叶孔板换热器基本单元综合评价系数
3 三叶孔板强化换热机理分析
3.1 基于场协同理论的三叶孔板强化换热机理分析
以上分析结果表明三叶孔板换热器较无孔板管壳式换热器壳程传热性能明显增强。但是传热系数和Nu数等只能宏观反映三叶孔板换热器的传热总体性能,而对于三叶孔板换热器的强化换热机理仍有待进一步分析。为此,本文对比了三叶孔板对于换热器壳程单元流道场协同性的影响[12]并据此分析其强化换热机理。
首先针对有/无三叶孔板的管壳换热器壳程速度、温度的协同性进行了直观图像分析。鉴于换热器内热对流、扩散过程的Peclet数通常较大,在此情况下通常不考虑纵向传热[13],因此在强化换热机理分析重点考虑横截面的流动换热行为。
在此过程中,以CASE-0和CASE-3作为无孔板换热器和三叶孔板换热器的典型代表,选取孔板后1cm截面(无孔板换热器截取对应位置截面)作为特征面对换热器壳侧流体的速度、温度截面分布特征及其协同性进行定性分析。两种换热器截面参数分布对比结果如图10所示,简单对比可以发现,对于无孔板的管壳式换热器基本单元,通过各等温线的平面二次流速度较弱,由此可能导致速度和温度梯度点乘的积分较小;而采用三叶孔板后截面速度明显增大(约3个数量级),为提高换热器热通量提供了条件。

图10 换热器单元流道横截面速度、温度场分布特征
场协同理论(field synergy principle)指出,速度场和温度梯度场的方向越接近平行,对流换热的协同性越好。换言之,在场协同角(synergy angle)β小于90°且接近0°,或者大于90°且接近180°的两种情况下换热器的场协同性较好。为了使协同性判别更为直观,通过重新定义协同角将其限定在[0,90]范围内,见式(5)[14]。
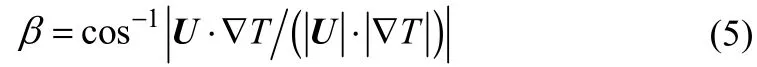
图11分别给出了两种换热器单元流道横截面的场协同角分布情况,可以看出对于无孔板管壳式换热器而言,其协同角β较小的位置主要集中在横截面几何中心处的小范围内,而在其他位置处β均接近90°,总体而言换热器的场协同性较差。相比之下,采用三叶孔板后,相同横截面几何中心处的场协同角明显减小;更为重要的是,场协同较低的强对流区间在整个截面内分布更为均匀,从而使换热器壳程的场协同性得到整体改善。
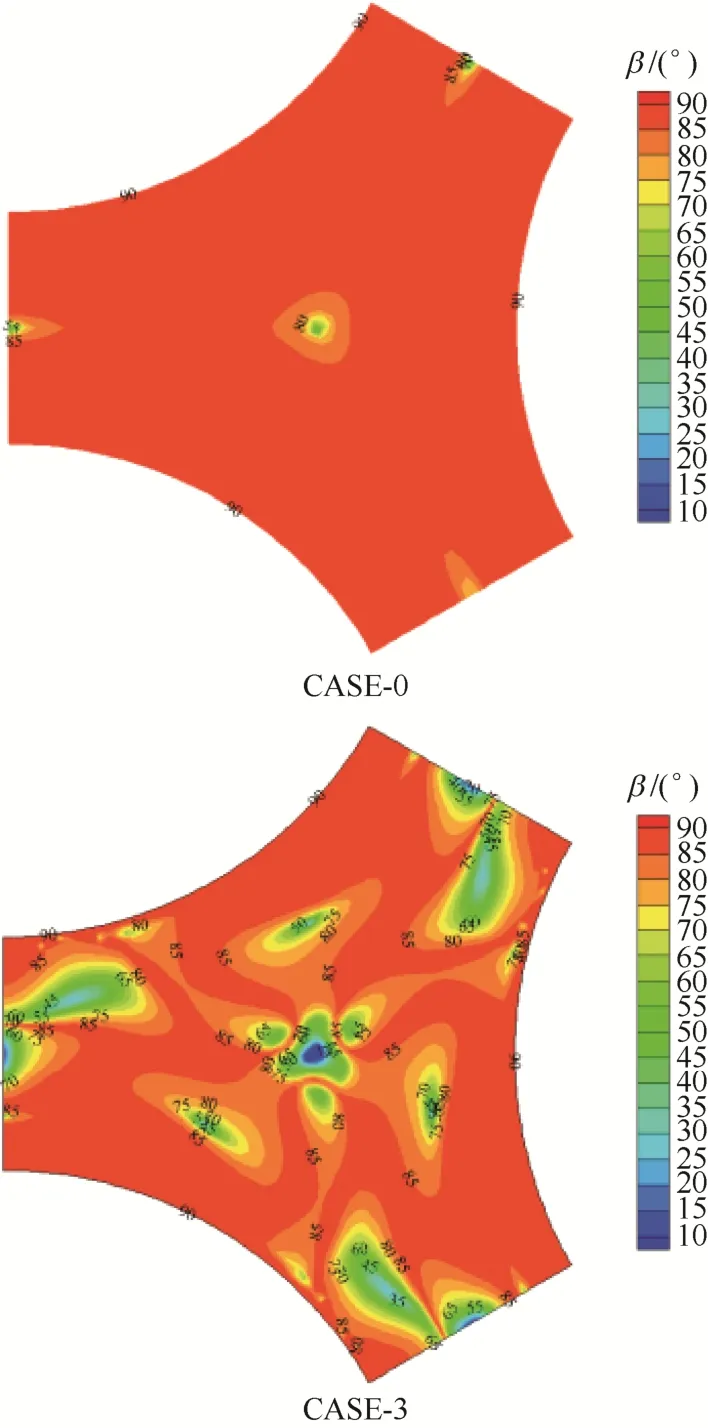
图11 换热器单元流道横截面场协同角分布
在此基础上,分别对有/无三叶孔板支撑的管壳式换热器场协同角进行面积平均和体积平均[15],见式(6)、式(7)。
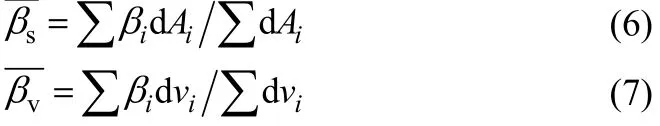
以此作为判据定量评估三叶孔板对换热器场协同性的提升效果。相同条件下各换热器模型的纵向分布情况如图12所示。
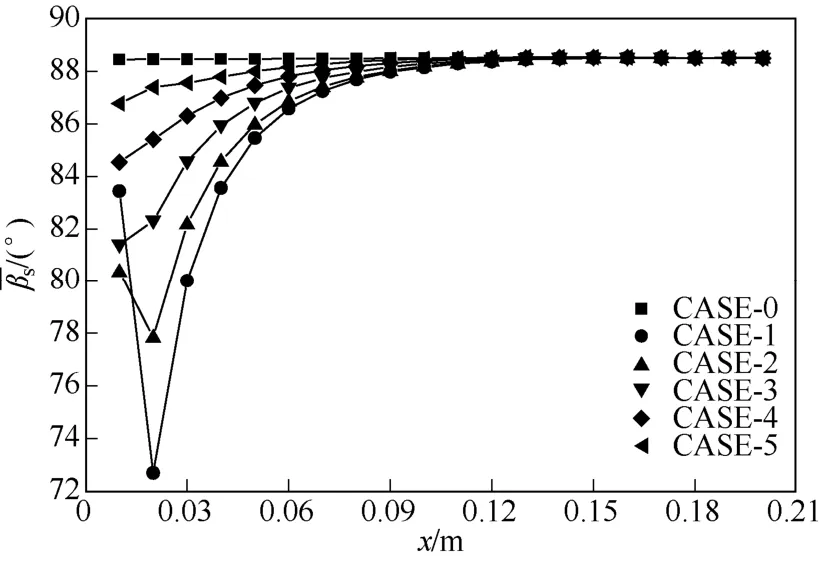
图12 三叶孔板换热器壳程单元纵向分布
图12的对比结果表明,三叶孔板换热器各纵向位置上的低于无孔板管壳式换热器,并且在距离孔板较近的位置处差异尤为明显。与后者在整个纵向范围内保持基本恒定的规律不同,前者随纵向距离总体呈现增加趋势,即距离孔板越近,强化换热作用越强。但是在间隙高度H较低的情况下出现例外性的先降后升,推测是由于在此情况下通过三叶孔后射流速度较大,而孔板后产生的回流导致其附近的场协同性稍差。另外,从的纵向增长规律可知,在三叶孔板后一定距离以外其对于改善换热器壳程场协同性的作用将不再明显,该距离可作为孔板支撑间距设计的一种参考。
不同孔高条件下三叶孔板换热器单元流道场协同角的体积平均值如图13所示。计算结果表明,三叶孔板换热器单元流道随H的增加而增加,这说明虽然减小H会影响三叶孔板后局部的传热性能,但是采用较小的间隙高度H可以从总体上提高三叶孔板换热器壳程的场协同性,从而进一步提高其强化对流换热能力。
3.2 基于纵向涡理论的三叶孔板强化换热机理分析
在管壳式换热器内采用强化换热结构必然使强化侧产生有旋流动,相关研究发现,不同流动状态下纵向涡的强化换热效果均优于横向涡,此即纵向涡强化换热的基本原理[16]。所谓纵向涡是指旋转轴方向与主流方向一致的流动涡旋,其大小定义为式(8)[17]。
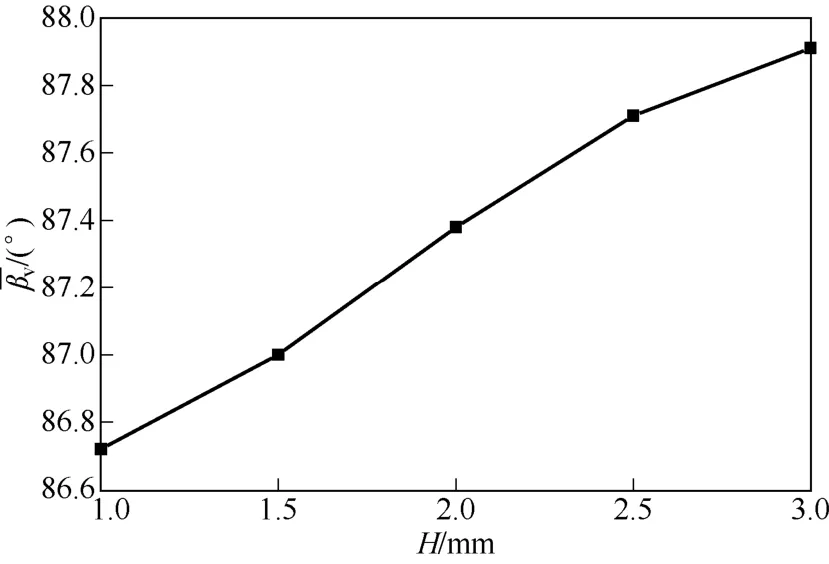
图13 孔高对三叶孔板换热器单元流道的影响
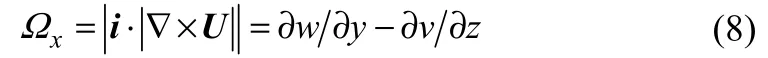
本文以CASE-0和CASE-3为代表对比了采用三叶孔板对换热器单元流道纵向涡结构的影响。如图14所示,对比结果表明采用三叶孔板前壳程单元流道纵向涡的影响范围小并且强度较弱;而采用三叶孔板后单元流道截面内的纵向涡分布区域及其强度均明显增大。由此可知,三叶孔板和管壁形成的通道间隙可以诱发壳程流体旋转形成纵向涡,进而促进主流区与传热壁面附近流体间动量与能量的交换,这从直观上解释了三叶孔板强化换热的原因。
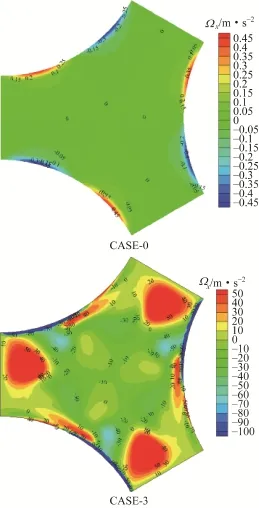
图14 管壳式换热器采用三叶孔板前后纵向涡分布
为了分析三叶孔板换热器壳程单元流道内纵向涡的一维分布规律,定义其面平均值为式(9)。
各横截面上如图15所示。统计结果表明,不同孔高的三叶孔板换热器值随截面到孔板距离均呈现先升高后降低的分布规律,因此壳程纵向涡强度在三叶孔板后的一定距离处均会出现极大值。这说明三叶孔板换热器壳程对流传热能力都在孔板后一定距离距离区间内达到最大,在该区间以外换热器壳程纵向涡强度逐渐减弱,对流换热性能也会有所降低。由此可知,保证壳程纵向涡强度可以作为孔板间距设计的另一种参考依据。
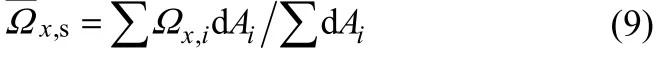
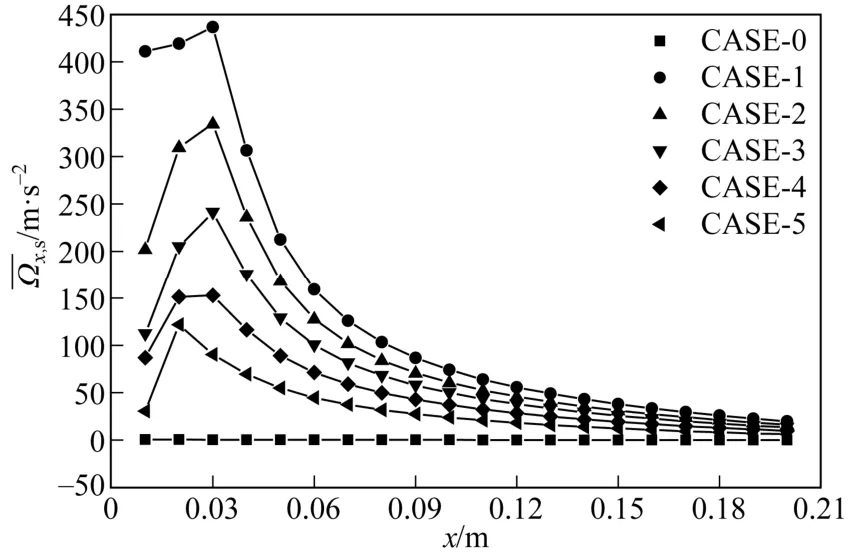
图15 三叶孔板换热器壳程单元纵向分布
4 结论
本文通过创建三叶孔板换热器单元流道模型对其壳程换热性能进行了数值计算,进而借助场协同和纵向涡理论分析其强化换热机理,得出以下结论。
(1)三叶孔板换热器传热Nu数和阻力系数f较无孔板管壳式换热器均有所增加,在孔高H≤3mm区间内PEC随孔高增大而增大。
(2)三叶孔板换热器壳程单元流道特征横截面内的二次流较强,存在较大范围的低场协同角区域,并且其在各纵向位置处的均小于无孔板管壳式换热器,说明前者速度-温度场协同性较好,从场协同角度解释了三叶孔板换热器强化换热的原因。
(3)三叶孔板换热器壳程单元流道内各纵向位置处纵向涡平均值均大于无孔板管壳式换热器,由此可根据纵向涡理论对三叶孔板强化换热机理进行解释。
(4)场协同和纵向涡强化换热理论均表明三叶孔板支撑间距存在最佳范围,不显著增大以及不显著降低可以作为指导支撑间距优化设计的两个参考依据。
符号说明
A——通流面积,m2
De——水力直径,m
f——阻力系数,量纲为1
f0——无孔板换热器阻力系数,量纲为1
H——开孔高度,m
——对流传热系数,W/(m2·K)
I——湍流强度,%
k——湍动能,m2/s2
L——分析通道长度,m
Nu——努塞尔数,量纲为1
Nu0——无孔板换热器努塞尔数,量纲为1
P——通流湿周,m
PEC——综合性能指数,量纲为1
Ro——换热管外半径,m
ReDe——基于水力直径的雷诺数,量纲为1
S——管间距,m
T——温度,℃
Tin——进口温度,℃
Tw——壁面温度,℃
U——速度矢量,m/s
uin——进口速度,m/s
β——速度-温度梯度场协同角,(°)
ε——湍流耗散率,m2/s3
λ——导热系数,W/(m·K)
——纵向涡强度,m/s2
——纵向涡强度面积平均值,m/s2
[1] 钱颂文. 换热器设计手册[M]. 北京:化学工业出版社,2002. QIAN S W. Heat exchanger design handbook[M]. Beijing:ChemicalIndustry Press,2002.
[2] 王秋旺,罗来勤,曾敏,等. 交错螺旋折流板管壳式换热器壳侧传热与阻力性能[J]. 化工学报,2005,56(4):598-601. WANG Q W,LUO L Q,ZENG M,et al. Shell-side heat transfer and pressure drop of shell-and-tube heat exchangers with overlap helical baffles[J]. CIESC Journal,2005,56(4):598-601.
[3] 汪淑奇,黄素逸. 纵流式换热器壳侧支撑方式的数值研究[J]. 化工学报,2007,58(5):1097-1103. WANG S Q,HUANG S Y. Numerical investigation on shell side support of longitudinal flow heat exchanger[J]. CIESC Journal,2007,58(5):1097-1103.
[4] 冯刚. 换热器管束流体诱导振动机理与防振研究进展[J]. 化工进展,2012,31(3):508-512. FENG G. Research progress in the flow induced vibration mechanism of tube bundles in heat exchangers and precautionary measures[J]. Chemical Industry and Engineering Progress,2012,31(3):508-512.
[5] 吴金星,魏新利,董其伍,等. 杆支撑换热器壳程的单元流道模型及流场分布[J]. 化工进展,2007,26(1):69-72. WU J X,WEI X L,DONG Q W,et al. Unit duct model and flow field distribution in shell side of rod baffle heat exchanger[J]. Chemical Industry and Engineering Progress,2007,26(1):69-72.
[6] 董其伍,白彩鹏,刘敏珊,等. 三叶孔板换热器壳程流体流动和传热研究[J]. 工程热物理学报,2013,34(1):115-117. DONG Q W,BAI C P,LIU M S,et al. Research on flow and heat transfer in shell-side of the trefoil-baffle support type heat exchanger[J]. Journal of Engineering Thermophysics,2013,34(1):115-117.
[7] 陶文铨. 数值传热学[M]. 2版. 西安:西安交通大学出版社,2006. TAO W Q. Heat exchanger design handbook[M]. 2nd ed. Xi’an:Xi'an Jiaotong University Press,2006.
[8] YAKHOT V,SMITH L M.The renormalization group,theε-expansion and derivation of turbulence models[J]. Journal of Scientific Computing,1992,7(1):35-61.
[9] 弗兰克 P. 英克鲁佩勒,大卫 P. 德维特,狄奥多尔L. 伯格曼,等. 传热和传质基本原理[M]. 葛新石,叶宏,译. 6版. 北京:化学工业出版社,2007:303. INCROPERA F P,DEWITT D P,BERGMAN T L,et al. Fundamentals of heat and mass transfer[M]. GE X S,YE H,trans. 6th ed. Beijing:Chemical Industry Press,2007:303.
[10] 焦兰. 三叶孔整圆形支撑板换热器的实验及数值模拟研究[D]. 武汉:华中科技大学,2011. JIAO L. Experimental study and numerical simulation of heat exchanger with triporate full circular supporting structures[D]. Wuhan:Huazhong University of Science & Technology,2011.
[11] WEBB R L. Performance evaluation criteria for use of enhanced heat transfer surfaces in heat exchanger design[J]. International Journal of Heat and Mass Transfer,1981,24(4):715-726.
[12] GUO Z Y,LI D Y,WANG B X. A novel concept for convective heat transfer enhancement[J]. International Journal of Heat Mass Transfer,1998,41(14):2221-2225.
[13] TAO W Q,GUO Z Y,WANG B X. Field synergy principle for enhancing convective heat transfer––its extension and numerical verifications[J]. International Journal of Heat and Mass Transfer,2002,45(15):3849-3856.
[14] 王定标,王宏斌,梁珍祥. 扭曲三叶管传热与流阻性能的数值研究[J]. 化工学报,2012,63(7):2064-2069. WANG D B,WANG H B,LIANG Z X. Numerical research on heat transfer and flow resistance performance of twisted trifoliate tube[J]. CIESC Journal,2012,63(7):2064-2069.
[15] 何雅玲,陶文铨.强化单相对流换热的基本机制[J]. 机械工程学报,2009,45(3):27-38. HE Y L,TAO W Q. Fundamental mechanism of enhancing single-phase convective heat transfer[J]. Journal of Mechanical Engineering,2009,45(3):27-38.
[16] MARTIN F. Embedded vortices in internal flow: heat transfer and pressure loss enhancement[J]. International Journal of Heat and Fluid Flow,1995,16(5):376-388.
[17] 童秉纲,尹协远,朱克勤. 涡运动理论[M]. 合肥:中国科学技术大学出版社,1994. TONG B G,YIN X Y,ZHU K Q. Eddy motion theory[M]. Hefei:Press of University of Science and Technology of China,1994.
Analysis on performance and mechanism of heat transfer enhancement of trifoil-hole baffle
WEI Zhiguo,LI Huafeng,KE Hanbing,ZHANG Kelong
(Science and Technology on Thermal Energy and Power Laboratory,Wuhan 2nd Ship Design and Research Institute,Wuhan 430064,Hubei,China)
Trifoil-hole baffle is a typical support plate which can improve heat transfer performance of tube and shell heat exchanger in the form of longitudinal flow,with many advantages such as smaller resistance and the ability of flow induced vibration weakening. In order to analyze the heat transfer enhancement effect and mechanism of trifoil-hole baffle on the shell side of tube and shell heat exchanger,a series of unit channel models for trifoil-hole baffle with different hole heightHwas built according to the periodical and symmetrical characteristics. The renormalization groupk-epsilon turbulence model and SIMPLE coupling algorithm were adopted for numerical simulation of shell side flow and comprehensive heat transfer performance evaluation. Results showed that Nusselt numberNuand resistance coefficientfof heat exchanger with trifoil-hole baffle are all larger than that without trifoil-hole baffle. Both the relative ratio ofNu/Nu0andf/f0decrease withHbut the value of performance evaluation indicators(PEC)increases with H. Besides,the surface average of synergy angle β is lesser and longitudinal vortex magnitude Ωx is larger for heat exchanger with trifoil-hole baffle compared with that without trifoil-hole baffle,which illustrate the improvement of field synergy and intensification of longitudinal vortex all contribute to the heat transfer enhancement of trifoil-hole baffle.
trifoil-hole baffle;heat transfer enhancement;comprehensive performance;mechanism analysis
TK124
:A
:1000–6613(2017)02–0465–08
10.16085/j.issn.1000-6613.2017.02.009
2016-06-29;修改稿日期:2016-08-03。
国家自然科学基金(51406138)及湖北省自然科学基金(2015CFB521)项目。
及联系人:魏志国(1984—),男,硕士,工程师。E-mail:za2002@163.com。

