证券公司效率与经济增长:理论框架与实证研究
翟永会

摘要:鉴于证券行业的特殊性,证券公司的效率始终游离于经济增长和金融发展关系的研究之外,文章考察了宏观经济增长对证券公司微观效率的影响和作用,在吸收和借鉴国内外已有理论并结合中国实际情况的基础上,建立了经济增长对证券公司效率影响的理论分析框架,并实证获得了经济增长不利于金融发展和证券业效率提升的证据,认为财政分权、政治集权的体制及经济增长方式的粗放性是背后的深层次原因,改革不尽合理的财政收入分配制度和地方官员考核晋升制度、适度调低经济增长目标、实现经济增长方式从粗放型向集约型转变有利于证券公司效率的提升。
关键词:经济增长;公司效率;Grange因果关系检验;脉冲响应函数
中图分类号:F224; F832.51
Abstract: Given the special nature of the securities industry, the securities company's efficiency has always been separated from the research of relationship of economic growth and financial development. This paper examines the efficiency and role of macroeconomic growth for securities company's micro-efficiency. Theoretical framework for economic growth affect the efficiency of the securities firm has been established by absorbing and learning the existing theories based on the actual situation in China. The evidence of economic growth is not conducive to financial development and securities company's efficiency has been obtained. The fiscal decentralization, institutional and political centralization and extensive mode of economic growth are the deep-seated reasons. The efficiency of securities companies can enhance by reforming unreasonable fiscal income distribution system and local officials assessment promotion system, Modesting reduction in the economic growth target, and achieving economic growth mode from extensive to intensive.
Key words: Economic Growth; Companies Efficiency; Grange Causality Test; Impulse Response Function
一、引言
经济增长和金融发展的关系是目前全球范围内备受关注和挑战的前沿课题之一,关于此论题目前尚未有明确结论,而证券公司作为重要的金融机构,关于其微观效率与经济增长关系的研究更是鲜有涉及。证券公司效率作为微观金融效率的一个重要分支,其与经济增长之间的关系是金融经济关系研究中不可忽视的因素。要研究这一论题,必须从金融全面发展的视角出发,不仅要研究经济增长对证券公司效率的影响,更要研究对与之密切相关的金融组织规模和效率的影响和作用,建立经济增长对证券公司效率影响的分析框架,吸收和借鉴国内外已有理论,并结合中国的实际情况,进行针对性分析。
现有文献中,几乎没有对证券公司效率与经济增长关系的直接研究,仅涉及金融效率和经济增长的关系,而且多把金融效率看作金融发展的一个侧面,从金融發展和经济增长关系的角度,来认识金融效率和经济发展的关系。关于金融发展与经济增长关系的认识,已有的理论大致可以分为三类:正相关论、负相关论和不相关论。根据对正相关关系的不同解释,正相关论又可以进一步细分为正向因果论、反向因果论、双向因果论和无因果论(统计现象论)。
正向因果论的论述,最早可以追溯到Schumpeter(1911)[1]。此外,Gurley & Shaw(1955)[2]、Goldsmith(1969)[3]和Hicks(1969)[4]均持有类似的观点,他们认为发达的金融系统可以把金融资源引导到生产率最高的用途上,这被形象的称为“供给领先”观点。关于反向因果论的论述,是由 Robinson(1952)[5]声称经济增长引致了对于金融服务需求,金融系统作为反应提供了这些服务,金融发展只是完全被动地适应经济增长的要求。反向因果论被归纳为“需求追随”。双向因果论则认为正向和反向因果关系均存在。内生金融发展和增长模型证明了两者之间互利的交互作用,这实际上说明因果关系可能是双向的。无因果论(统计现象论)认为经济增长和金融发展这种正相关关系仅仅是一种统计现象,并不意味着两者之间存在因果关系,两者之间的正相关关系,可能是由于两者均受某种共同因素的同方向影响造成。
与正相关论不同,负相关论的研究,则大都侧重于金融发展对于经济增长的负面影响研究。Jappelli & Pagano(1994)[6]年发表的著名文章,为主张金融部门发展和经济增长之间存在负相关关系的理论提供了依据。此外,Gregorio & Guidotti(1995)[7]也认为金融中介和经济增长之间的负相关关系,在不受管制的金融自由化和政府可能会采取救援行动预期的作用下,会发生逆转。在20世纪80年代,以Wijnbergen(1982,1983)[8][9]、Taylor(1983)[10]和Buffie(1984)[11]为首的新结构主义者提出的发展中经济体模型中,假定在发展中国家中可能存在一个竞争而又有效的场外市场或非机构信贷市场,在这种情况下,正规金融的发展,可能造成对场外交易的替代,从而不利于长期经济增长。同时,以股票市场为代表的直接融资体系同样有可能对经济增长产生不良影响。Kindleberger(1978)[12]指出,在过度杠杆放大情形下,预期不稳定性和资产投机可能对经济产生严重负面影响。非理性投资催生资产价格泡沫,泡沫将会破灭,由于银行系统的脆弱性,并引发经济危机。这个观点得到Singh(1997)[13]的进一步支持。
不相关论,是基于新古典增长理论的研究,其表明金融发展对经济增长的影响只有水平效应,没有增长效应。这样在长期内,金融发展和经济增长率就是不相关的。此外,根据Modigliani & Miller(1958)[14]的论证,在信息完备、任何经济活动都不存在交易成本的情形下,实际经济决策独立于金融结构。
上述文献均属于理论假说研究,而大多数实证检验出现在20世纪90年代以后,以King & Levine(1993b)[15]开创性工作为先导。根据实证研究采用的数据和方法不同,已有的实证大致可以分为横截面数据研究、时间序列研究和面板数据研究三种类型,由于不同经济体具有不同制度和结构特性,实证结果呈现很大差异: (一)基于截面数据的研究只是对于两者之间相关关系的检验, 根据对James(2008)[16]的总结中所涉及13项截面数据研究的统计,在13项研究中,有12项研究均支持正相关观点。(二)根据James(2008)中所涉及时间序列研究的统计,1984-2007年间共计有18项相关研究,其中有7项研究支持正向因果论,有6项研究提供了混合的证据,即在部分样本中发现了支持正向因果论的证据,在另一部分样本上发现了支持反向因果论的证据。(三)无论是采用截面数据还是时间序列数据的研究,样本容量太小引起的自由度问题会降低研究结论的可靠性,近年,有研究者试图用面板数据来扩充样本容量,根据James(2008)的总结,1995-2005年间的17项面板数据研究中,有10项明确无误的支持正向因果论。
目前国内部分学者也借鉴国外相关的研究思路与指标,运用计量经济手段对中国金融发展与经济增长关系进行了研究:根据本文的不完全统计,在25篇相关研究文献中,其中6篇进行了相关性分析,另外的文献集中于因果关系检验:(一)在6篇相关性分析文献中,除华晓龙等(2004)[17]的研究得出不相关结论外,其余研究均支持正相关结论。并且除华晓龙等(2004)的研究采用了截面数据外,其余5项研究均采用了时间序列数据,但上述6篇文献均在没有检验序列平稳性的条件下进行了回归分析,存在伪回归的可能,在研究方法上存在一定不足。因此,尽管其中部分文献声称发现了因果关系的证据,但严格来说其研究只能表明存在相关性。(二)在因果关系检验中,大部分研究都以Grange因果关系检验作为主要研究工具。根据我们的不完全统计,在18篇相关研究中,有8篇文献支持正向因果论,有6篇文献则证实了负向因果论,有4项研究则支持双向因果论,没有研究支持无因果论。其中周好文和钟永红(2004)[18]以及张珂等(2009)[19]的研究注意到了经济金融关系在不同地区表现形式的差异性。从数量上分析,存在因果关系的结论得到了绝大多数实证支持,但关于因果关系的方向,现有研究却不能达成一致。
综上可知,实证研究并不能给理论争论提供唯一正确答案。此外,已有实证研究,在数据选取或研究方法上还存在一些缺陷或不足:首先,由于缺乏发展中国家的足够时间序列数据,实证研究一直以多个国家的截面数据为主,以截面数据的单方程回归分析,来作为判断因果关系的依据,缺乏可靠的统计基础 ;其次,数据积累少,研究样本容量小,影响了结论的可靠性和稳定性,这一问题在针对中国的相关研究中更加突出 ;最后,个别研究在研究方法和工具使用上处理不够严谨,部分研究在进行格兰杰因果关系检验前没有进行协整检验,在研究方法和程序上存在缺陷 ,此外,根据Granger(1988)[20]的研究,即使在两非平稳变量之间存在协整关系,水平形式Granger因果检验此时也存在设定偏误,应使用误差修正模型(error correction model,ECM)形式的检验,但除王志强和孙纲(2003)[21]以及周好文和钟永红(2004)的研究外,其余的文献均采用了水平形式Granger因果检验。
既有研究表明,經济增长和金融发展关系的研究目前仍尚无定论,而作为微观金融效率的一个重要分支,证券公司效率是金融经济关系研究中不可忽视的因素,但目前证券公司(或投资银行)的效率始终游离于经济增长和金融发展关系的研究之外,本文试图在这方面做有益的尝试,创新之处在于:(一)以往基于新古典经济增长理论的研究范式对企业效率和经济增长的研究,多是强调企业效率或生产率(主要是制造业)对宏观经济增长的影响和贡献,本文的研究考察了宏观经济增长对证券公司微观效率的影响和作用,在吸收和借鉴国内外已有理论并结合中国实际情况的基础上,建立了经济增长对证券公司效率影响的理论分析框架,基于这一框架进行的理论分析表明,经济增长率提高会对证券公司效率造成负面影响;(二)鉴于以往实证研究之不足,本文采用月度数据扩充数据量,并在Grange因果关系检验基础上利用VECM模型进行实证检验,得到支持理论假说成立的结论。
二、经济增长与证券公司效率:一个理论分析框架
本文认为中国经济增长和证券公司效率的关系更多的是呈现负相关特征,并且在中国造成这种负相关关系的原因可能是反向的,即存在经济增长对证券公司效率和金融发展的负面影响,具体的分析思路见图1:
财政分权是中国转型经济中最重要体制设计之一,中国的财政分权改革是在垂直的政治管理体制内进行的,因而同时具备经济上分权和政治上集权的双重特征。为防范经济分权后地方政府的“机会主义行为倾向” ,经济增长指标成为中央政府衡量地方政府绩效的核心指标,并将地方政府官员的政治升迁和经济增长指标挂钩。这样的财政收入分配体制和政治激励机制就形成了地方政府和地方政府官员追逐经济增长的强烈冲动 ,中国地方政府之间关系最终表现为“为GDP增长而竞争”。
另一方面,地方政府主导的地区间GDP增长竞争不可避免地加剧了以低价格要素大量投入为基本特点的经济增长方式,在这样的背景下,增加资本和劳动等要素投入而不是提高全要素生产率成为首要选择。地方政府的增长冲动就转化为投资冲动。相对不足的地方财力,相对于提高经济增长率和增加投资的冲动显得捉襟见肘。由于金融资金与政府支出和投资的高度互补性,地方政府对金融运行和金融资源配置的干预成为必然选项。
迄今为止,国内研究只注意到了地方政府干预对信贷资源配置效率的影响。这种干预在最初体现为对国有商业银行信贷资源配置的干预,这导致国有银行体系产生大量呆坏账和不良资产。其实,地方政府干预金融资源配置还有另外一条途径,那就是对证券市场运行进行直接和间接干预。地方政府对证券市场干预的最直接表现是不遗余力扶持当地企业上市,除此之外,地方政府对证券市场的干预更多的是通过对中央政府和监管当局的游说,通过中央政府和监管当局的行动来实现。
根据我们建立的分析框架,在财政分权和政治集权的体制下,政府具有追求高增长的强烈冲动,这种冲动造成了地方政府以及在地方政府游说和压力下中央政府和监管当局对金融运行的干预,这种干预对证券公司效率形成了一种负向冲击(见图2)。并且地方政府追求经济增长的动机越强,设定的增长目标越高,这种负向冲击就会越大。这样一个分析框架为经济增长对证券公司效率和金融发展的负面影响提供了一种解释。为检验这一框架在中国是否成立,我们进行了实证检验。
三、 经济增长与证券公司效率关系的实证检验
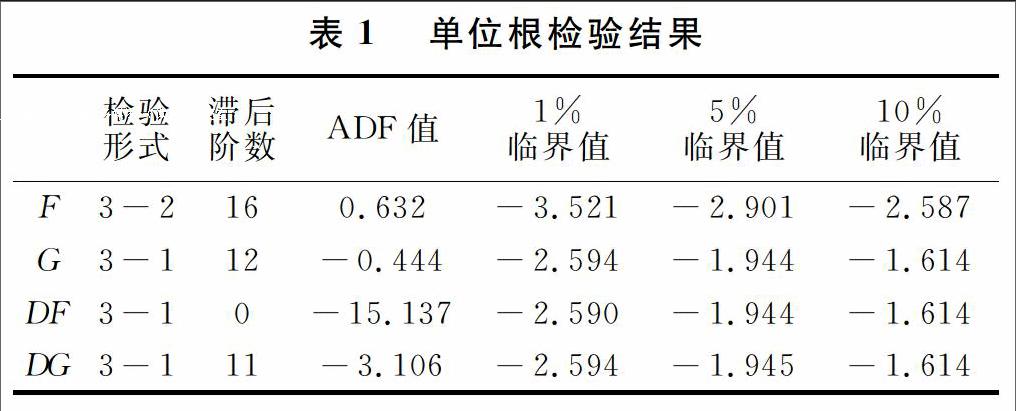
为了扩充样本容量,本节采用了月度数据,用工业增加值月增长率来度量经济增长(工业增加值数据来源为Wind资讯金融数据库)。证券公司效率由于缺少相应的月度数据无法直接通过计算获得,本文利用交易所中每个交易席位所完成的平均交易额来表示证券公司的效率。对股票市场交易额和上证综合指数进行Spearman检验的结果表明,两者间的相关系数为0.886,而且这种相关关系在1%的水平下显著。因此,每个席位股票市场的交易额除受证券公司效率影响外,还要受股票市场行情起伏的影响。为比较准确的衡量证券业效率,在计算每个席位的平均交易额前,应剔除股市行情变动的干扰。为此,我们用股票市场的交易额除以上证综合指数得到以1990年12月19日的不变价格度量的实际交易额,用实际交易额比交易席位数,得到每个席位的平均交易额。考虑到证券公司一般在深圳和上海同时开户并设有席位,席位总数采用深圳证券交易所的席位总数,数据来源为《深圳证券交易所市场统计年鉴》。每个席位月平均交易额序列和工业增加值增长率序列分解记为F和G。样本数据的时间区间为2002年1月至2014年9月。本节借助VAR模型和Grange因果关系检验来判定我国经济增长和证券公司效率之间的因果关系。建立VAR模型的前提是待检验的序列必须是平稳序列或同阶单整且存在协整关系。因此,我们首先需要进行ADF检验,来判断相关序列的平稳性。
(一)序列平稳性的ADF检验
与方程(2)相比,方程(3)中增加了截距项,而方程(4)中增加了截距项和时间趋势项。
利用ADF检验来判断序列平稳性,事先必须解决两个问题:首先,是检验形式的选择问题。检验形式的選择,我们采取观察序列的方法,若变量序列的数据呈现出无规则上升和下降,并重复这一状况,说明数据主要由随机趋势所支配,因而我们选择方程(2)作为估计模型;若数据呈现随时间逐渐上升或下降的趋势并且这种趋势不太陡峭,则说明数据主要由随机趋势和固定趋势联合支配,我们选择方程(3)作为估计模型;若数据呈现随时间迅速上升或下降的趋势,则说明数据主要由时间趋势所支配,我们可以选择方程(4)作为估计模型 。其次是滞后阶数p的确定。在上述三个检验模型中加入滞后差分项的目的,是为了防止残差项可能存在的自相关,但过多滞后项又会引起不必要的信息损失。滞后阶数p的确定,我们依据的原则是,根据序列的长度给出一个上限,然后由EViews软件基于最小信息准则(AIC)来确定实际滞后阶数。
由数据可以看出,F呈明显的上升趋势,并且这种趋势不太陡峭,我们对其采用方程(3)的检验形式;G呈无规则升降,我们对其采用方程(2)的检验形式。设定滞后阶数的上限为30,EVIEW软件依据AIC准则自动确定的滞后阶数分别16、12,检验结果见表1:
检验结果表明,两个序列的ADF统计量均大于10%的显著性水平下对应的临界值,存在单位根的原假设不能被拒绝,因而证券公司效率序列和工业增加值增速序列均为非平稳序列。为了判断两序列是否为同阶单整序列,我们继续对其一阶差分序列进行检验。分别用DF、DG表示其一阶差分。EViews软件依据AIC准则,对两个差分序列自动确定的滞后阶数分别0、11。检验结果见表1。两个差分序列的ADF统计量均小于1%显著性水平下的临界值,这说明我们均可以以99%的置信度拒绝存在单位根的原假设。从而DF、DG均为平稳序列。这样序列F和序列G均为I(1),满足协整检验的前提。下面继续检验是两者之间是否存在协整关系。
(二)协整关系检验
协整的经济意义在于两个或多个变量虽然它们有各自的长期波动规律,但是如果它们是协整的,那它们之间就存在着一个长期稳定的比例关系即这些变量之间不能互相分离太远。序列F与G之间的协整关系检验采用Johansen检验。协整检验同样要面临两个事先的选择:
一个是滞后阶数的选择。一般而言,滞后阶数可以通过似然比统计量、AIC准则、SC准则来确定。
二是需要确定检验形式。Johansen协整检验包含五种可能的形式:
1.序列没有确定趋势,协整方程没有截距。
2.序列没有确定趋势,协整方程有截距。
3.序列有线性趋势,协整方程仅有截协整距。
4.序列和协整方程都有线性趋势。
5.序列有二次趋势且协整方程有线性趋势。
F序列具有明显的非随机趋势,因此我们选择选项4。依据AIC准则,所选择的最大滞后阶数分别为18,检验结果见表2:
检验结果表明,无论是采用迹统计量方法,还是采用最大特征值统计量方法,在5%的显著性水平下,不存在协整关系的原假设总是可以被拒绝,因此,在F和G间存在协整关系。这样的结果,意味着具备了利用VAR模型进行Granger因果关系检验的前提条件。
(三) Granger因果关系检验
根据Granger(1988)的研究结论 ,两变量之间存在协整关系,那么也一定存在Granger因果关系。因此,检验的重点不在于是否存在因果关系,而在于因果关系的方向。但此时,传统的Granger因果检验存在设定偏误,应使用误差修正模型(error correction model,ECM)形式的检验。为此,我们以F和G为基础建立如下向量误差修正模型(vector error correction model,VECM),来进行因果关系检验:
在方程(5)中,待检验的原假设为 ,如果原假设不能被拒绝,则意味着DG的滞后项对F取值没有影响,同时表示F和G之间长期均衡关系的误差修正项 对F取值也没有影响,即G不是F的格兰杰原因。同样,在方程(6)中,原假设 不能被拒绝则表明,F不是G的格兰杰原因。
Gujarat(1995)[22]指出,Granger 因果检验的结论对滞后阶数高度敏感,因此在实际使用过程中必须格外小心。因此,利用VECM进行的格兰杰因果关系检验,滞后阶数的选择十分关键,选择不同的滞后阶数有可能获得不同的检验结论。VECM滞后阶数的选择我们利用其对应的水平状态的VAR模型(7)来确定。
VAR模型滞后阶数的判定,通过如下两个步骤:首先确定一个最大滞后阶数; 其次,利用滞后长度标准选择最为合适的实际滞后阶数。
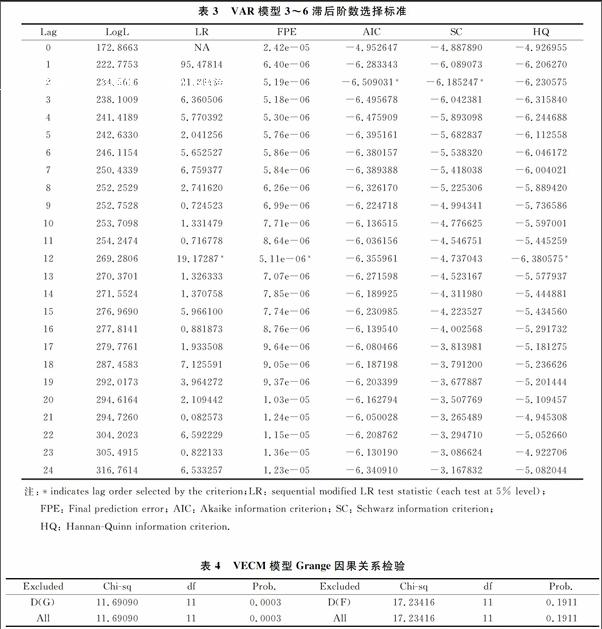
根据张成思(2008)[23]推荐的标准,月度数据可以考虑的滞后阶数是12、18或24。我们总共有93个样本点,在双内生变量VAR模型容许的最大滞后阶数为30。Granger因果检验的结论对滞后阶数很敏感,因此一个可靠的做法是从一个尽可能大的滞后阶数开始。综合数据自身特征和Granger因果检验的要求两方面因素,我们设定最大滞后阶数为24。表3给出了VAR模型在最大滞后阶数为24时的滞后阶数长度选取标准。尽管在5种选择标准未能作出完全一致的选择,在5%的水平下,其中似然比检验(LR)、最终预测误差(FPE)和HQ信息准则给出的最优滞后阶数均为12,因此我们设定模型3-6的最佳滞后阶数应该为12。由于VECM的滞后阶数是针对一阶差分项而言,因此其滞后阶数会比对应的水平形式VAR模型低1。综上,我们设定VECM的滞后阶数为11:
表4中的结果表明,在方程3-4中, 的假设在5%的常用显著性水平下可以被拒绝。在方程(6)中, 的假设则不能被拒绝。对于VECM模型,现有计量工具中的Grange因果检验选项仅检验一阶差分滞后项的系数是否联合为0,不检验误差修正项的系数是否为0,因而不能单独依此直接作为判断因果关系的依据,需要综合考虑对误差修正项系数的检验结果:
誤差修正项的估计值的t-统计量服从自由度为59(等于样本数92减去待估参数23)的T分布,在5%的显著性水平下,对应临界值为2.000。表5中误差修正项系数的估计结果表明,因此,方程3-4中 的t统计量绝对值大于对应的临界值, 的假设可以被拒绝。方程3-5中对应t统计量绝对值小于对应的临界值, 的假设不能被拒绝。而且误差修正项系数绝对值大于1,这意味着这一方程不会收敛于长期均衡状态。
综合来看, 不成立,这意味G是F的格兰杰原因,并且这种因果关系不仅在短期,而且在长期均是存在的。 则不能被拒绝,这表明F不是G的格兰杰原因。同时也表明了证券公司效率对经济增长的影响不仅在长期而且在短期是可以被忽略的。
格兰杰因果关系检验的结果只表明了存在从经济增长到证券公司效率的因果关系,但经济增长对证券公司效率的作用是正向的还是负向的,上述检验并不能给出直观而又有效的回答。对于两者之间长期的因果关系,可以通过方程3-4中误差修正项的系数(估计结果见表6)来判定:
从方程(8)来看,经济增长对证券公司效率的长期影响显然是负向的。至于经济增长对证券公司效率的短期影响,则需要借助脉冲响应函数(Impulse Response Function)进一步分析。
(四)基于脉冲响应函数的进一步分析
脉冲响应函数是用来衡量随机扰动项的一个标准差冲击对其它变量当前和未来取值的影响轨迹,它能够比较直观地刻画出变量之间的动态交互作用及效应。利用VAR模型进行脉冲响应函数分析的前提是,VAR模型必须是平稳的。为此,在保证模型平稳性的条件下,我们选择一个尽可能大的滞后阶数24开始试验,依次降低滞后阶数。结果发现滞后14阶以上的VAR模型无法满足稳定性要求,从滞后14阶开始,VAR模型可以满足稳定性要求。表7给出了对滞后14阶模型3-6的进行平稳性检验的AR根:
滞后14阶、含有2个内生变量的VAR模型3-6共有28个根(12乘以2),从表中可以看出,VAR模型的所有根模的倒数均小于1,即均位于单位圆内,因而该模型是平稳的。
另外,由于脉冲响应函数对冲击的顺序非常敏感,根据Sims(1980)[24]提出的排序,应该先是不易受影响的变量(如弱外生变量),后是与之相关的内生变量,最后是其它内生变量。工业增加值序列与证券公司效率序列比较,后者对外界冲击的反应更加敏感。因此我们设定的冲击顺序为G、F。
我们设定追溯期数为60(即5年),用残差协方差矩阵的Cholesky因子的逆来正交化脉冲,在估计残差协方差矩阵利用Cholesky因子分解时进行了小样本自由度修正,获得了对G施加一个标准新息(Innovation)冲击,引起的F的脉冲响应函数及累计脉冲响应函数曲线(见图3)。从图中可以看出,给G施加一个标准新息冲击对F以后各期取值的影响,随着追溯期数的增加,呈现以负值为主、不断衰减、最后收敛于0的趋势。但从累计脉冲响应函数的估计值分析,无论在短期还是在长期,全部为负值。这说明,经济增长率提高对证券公司效率的的总体影响无论在短期内还是长期都是负向的。
检验结果表明,存在从经济增长到证券公司效率的Grange因果关系,而且这种因果关系无论在长期或短期均存在,并且经济增长率提高对证券公司效率的累计影响无论在短期还是在长期均是负向的。这样的结果与我们提出的经济增长会对证券公司效率造成负面影响的分析框架相一致。
理论推演及实证检验的结果均表明经济增长率的提高不利于证券公司效率的提升,这意味着在经济增长和证券公司效率之间存在潜在矛盾,在这种情况下,究竟该如何权衡取舍,这需要考虑是否有利于金融全面发展和金融资源的有效配置。
四、结论
本文从金融全面发展的视角出发,首先提出了一个关于证券公司效率和经济增长关系的理论分析框架:经济增长对证券公司效率会造成负面影响。提出这样的论断是基于两个方面的原因,一是财政分权、政治集权的特殊体制,二是不合理的经济增长方式。紧接着利用Grange因果关系检验和脉冲响应函数进行的实证表明,这一分析框架是成立的,这意味着在经济增长和证券公司效率之间存在潜在矛盾。在这种情况下,究竟该如何权衡取舍,需要考虑是否有利于金融全面发展和金融资源的有效配置。证券公司效率提高对于资本市场发展以及金融的全面发展具有重要意义。因此,有必要為证券公司效率提升和金融全面发展创造条件,具体而言:(一)从源头上需要改革不尽合理的财政收入分配制度和地方官员政绩考核晋升机制, 改变地方政府在现有的财政体制下过度追求地方经济利益最大化、片面追逐经济增长的行为,转变中国地方政府之间 “为GDP增长而竞争”的状态,不以经济增长率作为衡量地方官员政绩的主要考核指标,短期内中央政府应适度调低经济增长目标,在“新常态”下转变经济发展方式,加快实现经济增长方式转变的步伐,经济增长不再以单纯依靠增加资本和劳动等要素投入的投资拉动为主,应向提高全要素生产率转变。(二)政府部门应减少对证券市场运行进行过度的干预。正如干预信贷资金配置不利于商业银行经营效率提升一样,对证券市场的干预,则有会对证券公司效率造成负面影响和作用,因此,一方面,地方政府应转变在强烈增长冲动和投资冲动的作用下,“不遗余力” 扶持当地企业上市以弥补地方政府财力不足和拉动当地经济增长的行为,另一方面,应改变当前中国股市二级市场极具特色的政策市循环现象,事实上,二级市场政策市对证券公司的效率提升具有很大消极作用,在此环境下,证券公司不再致力于加强经营管理、提高服务能力,而是积极打探各种消息,利用这些消息作自营或及时把它们提供给客户以增加其交易量,因此若想提高证券公司效率必须改变当前的政策市现象,使证券市场在效率提升的竞争中真正发挥其市场融资的功能。

