基于结构模态的机翼带吊舱有限元建模方法

李阳, 刘颖

(中国飞行试验研究院 飞机所, 陕西 西安 710089)

基于结构模态的机翼带吊舱有限元建模方法

李阳, 刘颖

(中国飞行试验研究院 飞机所, 陕西 西安 710089)

针对无有限元模型的颤振计算建模问题,提出了一种采用结构优化方法建立有限元模型的方法。依据标准算例的结构尺寸和材料特性建立其有限元模型,采用集中质量单元和连接杆模拟外挂吊舱结构,得到了机翼带吊舱的标准模型。计算其结构模态并作为优化目标,建立几何尺寸、质量与标准模型一致。但结构参数不一致的初始模型;然后采用敏度优化算法优化初始模型,得到机翼带吊舱的优化模型。计算结果表明,优化模型与标准模型的颤振速度和频率均较为接近。

结构模态; 敏度优化算法; 颤振分析

0 引言

随着航空试飞能力的发展,大量的航空设备、机载系统需要进行它机试飞,以验证其在真实环境下的性能及与飞机的相容性。由于飞机机体空间有限,因此这些设备大多作为外挂吊舱的形式挂于机翼下方。吊舱种类多样,气动外形、结构质量刚度特性各异,与机翼气动力耦合严重,对挂载平台的影响很大,需要进行颤振特性分析评估,以确保飞行安全。常规的方法是从原机模型出发,建立带外挂的有限元模型,然后进行地面共振试验,修改模型,经过一系列迭代,最终才能得到较为准确的结果[1]。然而该方法过程繁杂,且在实际工程应用中某些机型无法获得原机结构有限元模型,因此迫切需要一种简便、实用的机翼带外挂物建模方法，以便高效地解决上述问题。

李阳等[2]已经发展了一种无外挂机翼的结构动力学建模方法,并以一个标准模型为参考,对该方法进行了验证。本文在此基础上增加外挂吊舱,计算结构模态参数,并以此作为优化目标,采用结构优化的方法,建立了一个机翼带外挂物的有限元模型,划分了气动力网格和结构网格,计算了机翼带外挂物的颤振速度,得到了较为满意的结果。

1 理论基础

1.1 模态分析

结构的模态分析方程一般可表示为[3]:

(1)

式中:K和M分别为刚度矩阵和质量矩阵;λ和φ分别为特征值和特征向量。

1.2 颤振分析

V-g法和p-k法是两种最主要的颤振分析方法。相对而言,p-k法能够更加贴近试验结果。p-k法颤振分析方程为[4]:

(2)

式中:V为来流速度;b为参考半弦长;p为特征值;B为阻尼矩阵;K为减缩频率;Q为非定常气动力矩阵;下标hh表示模态分析集h-set;上标R表示实部;上标i表示虚部。

1.3 优化方法

模型优化涉及的优化研究是一个标准的优化问题,即在ndv维空间中搜索一组设计变量使得目标函数F(v)最小化[5],如式(3)所示[6]。

(3)

式中:gj(v)指定了不等式约束条件,又称性能约束,如颤振速度约束、发散速度约束、变形约束、强度约束、副翼效率约束等;vi指定了设计变量的上下限,又称边界约束。

本文采用敏度优化算法对设计对象进行优化设计[3]。敏度优化算法是一种根据函数的梯度信息进行数值搜索、比较适合结构详细设计阶段的优化方法,能快速地收敛于最优解,计算效率高。目前,该类方法是结构多学科优化和气动弹性多学科优化中普遍使用的方法,其计算流程如图1所示。

图1 敏度优化算法流程图Fig.1 Flow chart of sensitivity optimization algorithm

2 模型优化

2.1 标准算例

本文采用AGARD445.6机翼作为标准算例。AGARD445.6机翼是美国NASA兰利研究中心用于风洞颤振试验的一个国际上公认的跨声速标准颤振计算模型,国内外大量的颤振算法的验证标模均采用该模型[7]。AGARD445.6机翼翼型为 NACA65A004,是具有明显跨声速气动特性的变厚度薄形机翼,展长为762 mm,1/4弦线的后掠角为45°,展弦比为1.62,根稍比为0.66,机翼平面形状如图2所示。

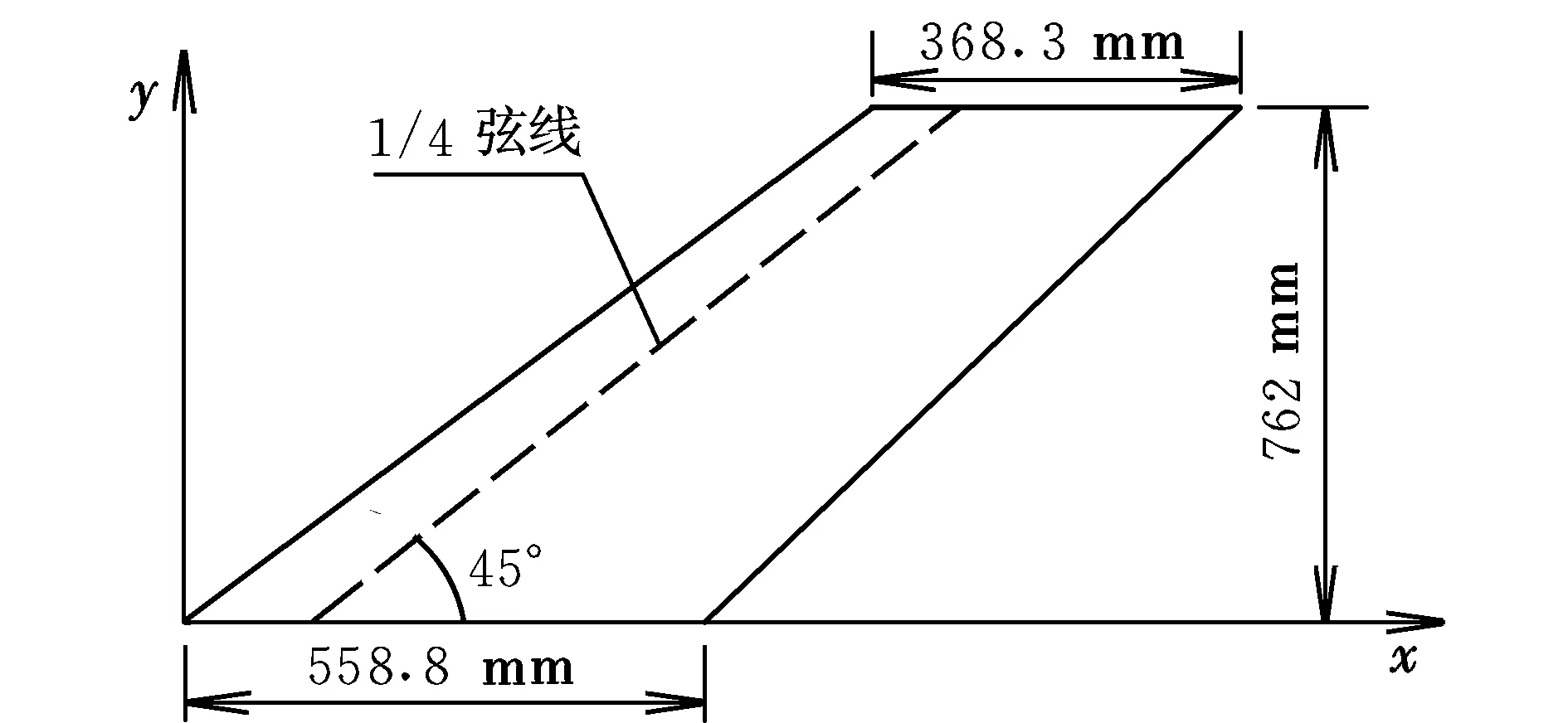
图2 AGARD445.6机翼平面形状Fig.2 Layout of AGARD445.6 wing

AGARD445.6机翼采用材质均匀的层合板制成,机翼材料和模态频率的试验值如表1所示。

表1 AGARD445.6机翼材料和固有频率

依据AGARD445.6机翼的几何外形和材料特性,建立了标准算例的有限元模型,并加入外挂物模型。采用集中质量单元模拟外挂物质量分布,梁单元模拟吊舱与机翼的连接刚度及吊舱的刚度分布。其中,在图3所示吊舱部位分布3个集中质量单元,每个质量单元0.3 kg,模型总重2.7 kg。得到机翼带吊舱的三维有限元模型,简称标准模型。

图3 AGARD445.6机翼带外挂物标准有限元模型Fig.3 Reference FE model of AGARD445.6 wing with pods

对上述结构模型进行有限元模态计算,计算模态如表2所示。

表2 AGARD445.6标准模型计算模态

2.2 模型优化及结果分析

建立AGARD445.6机翼有限元模型,其中沿着弦向划分4个单元,展向划分8个单元,单元数共32个。单元初始厚度均为10 mm,初始密度为527.8 kg/m3。采用集中质量单元模拟吊舱质量分布,梁单元模拟吊舱与机翼的连接刚度及吊舱的刚度分布。其中,在图4所示吊舱部位分布3个集中质量单元,每个集中质量单元0.3 kg,模型总重2.7 kg。得到机翼带吊舱的三维初始有限元模型。分别选取翼尖前缘点、翼尖后缘点为振型优化点,对带吊舱机翼的前5阶固有频率及振型进行优化。由于缺少机翼振型的试验数据,故翼尖振型值采用标准模型计算值作为优化目标。

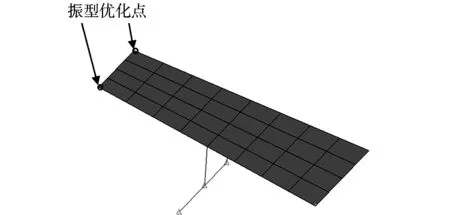
图4 AGARD445.6机翼带外挂物初始有限元模型Fig.4 Initial FE model of AGARD445.6 wing with pods

已知条件:已知机翼的平面形状、总体质量、前五阶模态的频率及振型。

目标函数:机翼一阶弯曲频率及振型、吊舱俯仰频率、机翼二阶弯曲频率及振型、吊舱偏航频率、机翼一阶扭转频率及振型与实验结果接近。

设计变量:机翼厚度分布、机翼材料密度、吊舱连接刚度。

约束条件:(1)质量约束,调节机翼密度使得在优化计算中保持机翼质量不变;(2)厚度约束,机翼厚度最小不低于1 mm,最厚不超过25 mm;(3)频率约束,约束前5阶模态频率;(4)振型约束,约束机翼前3阶模态对应点的振型值。

表3和表4分别给出了优化前后机翼的频率和振型对比。

表3 计算频率对比

表4 计算振型对比

与标准模型对比,优化后频率除机翼一阶弯曲和吊舱偏航模态外,其余模态误差均较小,所有模态频率误差不超过21%。因为翼尖前缘振型值较小,所以相对误差较大,但总体都在可接受范围内。

3 算例计算

采用AGARD445.6机翼为算例,对机翼带吊舱的颤振速度和颤振频率进行计算和比较。计算中采用升力面模拟机翼和竖直板的非定常气动力,采用升力体模拟吊舱并考虑3个部件非定常气动力之间的相互耦合影响[8]。其中,吊舱距离翼面100 mm,吊舱直径25 mm,长600 mm,如图5所示。

图5 机翼带吊舱气动模型Fig.5 Aerodynamic model of wing with pods

在海平面及Ma=0.5工况下,计算该模型前五阶模态颤振速度和颤振频率,得到其标准模型和优化模型的V-g和V-f结果分别如图6和图7所示。

由图6可以看出,在Ma=0.5工况下的颤振速度和颤振频率分别为150 m/s和14.9 Hz。颤振形式为一阶弯曲和吊舱俯仰耦合颤振。

由图7可以看出,在Ma=0.5工况下的颤振速度和颤振频率分别为160 m/s和13.6 Hz。颤振形式为一阶弯曲和吊舱俯仰耦合颤振。

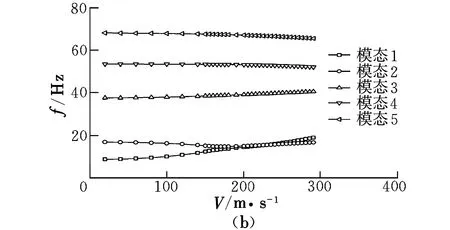
图6 标准模型的V-g和V-f结果Fig.6 V-g/V-f results of reference model

图7 优化模型的V-g和V-f结果Fig.7 V-g/V-f results of optimized model

综上所述,本文优化模型可以相对准确地计算出机翼带吊舱的颤振速度和颤振频率,与标准模型相比,优化模型的颤振速度误差为6.67%,颤振频率误差为-8.7%。

4 结束语

本文开展了利用结构模态参数,建立机翼带吊舱动力学模型的建模方法研究。该方法利用敏度优化方法,以机翼结构厚度、密度、吊舱连接刚度作为设计变量,结构模态频率和振型作为目标函数,建立了机翼带吊舱的优化模型。经与标准模型颤振计算结果的对比,表明本文所建立的优化模型能够较好地预估颤振速度和颤振频率。针对带外挂物复杂结构的颤振分析问题,可以开展地面模态试验,取得真实模态值后,采用此种优化方法,建立有限元模型,开展颤振分析。

[1] 陈桂彬,邹丛青,杨超.气动弹性设计基础[M].北京:北京航空航天大学出版社,2004:148-149.

[2] 李阳,寇宝智.一种基于模态试验的结构动力学建模方法[J].飞行试验,2016,32(1):1-5.

[3] 龚尧南.结构力学[M].北京:北京航空航天大学出版社,2001:110-114.

[4] 赵永辉.气动弹性力学与控制 [M].北京:科学出版社,2007:224-258.

[5] 谭申刚,万志强.基于现代优化方法的气动弹性建模与设计技术[J].工程力学,2008,25(8):235-240.

[6] 王伟,杨伟,赵美英.多工况下机翼结构优化设计方法研究[J].强度与环境,2007,34(3):18-22.

[7] 吕斌,谭申刚,万志强,等.T型尾翼气动弹性优化设计[J].北京航空航天大学学报,2007,33(4):409-413.

[8] 万志强,唐长红,邹丛青.柔性复合材料前掠翼静气动弹性分析[J].复合材料学报,2002,19(5):118-124.

(编辑：李怡)

Finite element modeling method based on structural mode for wings with pods

LI Yang, LIU Ying

(Aircraft Flight Test Technology Institute, CFTE, Xi’an 710089, China)

This paper presents a method for finite element (FE) modeling with structural optimization method for flutter analysis without the wing FE model. A reference FE model was established by adding the pods to a standard wing FE model. An initial model was also built with the same geometry and mass as the reference model. Taking the structural modes of reference model as the objective, the optimization of initial model was conducted by means of sensitivity algorithm. Calculation results show that the flutter speed and frequency of the optimized model approximate those for the reference model.

structural mode; sensitivity optimization algorithm; flutter analysis

2016-05-11;

2016-09-05;

时间:2016-11-10 09:10

李阳(1987-)，男，江苏镇江人，工程师，硕士，研究方向为结构动力学。

V215.3

A

1002-0853(2017)01-0093-04