干扰和执行器故障系统的自适应神经网络控制
王丽, 刘春生
(1.南京航空航天大学 自动化学院, 江苏 南京 210016;2.南京航空航天大学 金城学院, 江苏 南京 211156)
干扰和执行器故障系统的自适应神经网络控制
王丽1,2, 刘春生1
(1.南京航空航天大学 自动化学院, 江苏 南京 210016;2.南京航空航天大学 金城学院, 江苏 南京 211156)
针对一类存在未知外部扰动和执行器故障的过驱飞行器系统的控制问题,提出了一种非线性自适应控制方案。在自适应控制方案中,设计了神经网络补偿算法逼近未知干扰项来消除环境干扰对系统的影响,提高了系统的鲁棒性。同时,控制律的输出作为控制分配器的输入,设计自适应控制分配算法来补偿执行器故障或输入饱和,从而提高了系统的稳定性和操作性,并利用李亚普诺夫稳定理论证明了所设计的控制系统能使误差系统最终一致渐近有界。最后,给出了一个数值仿真算例,验证了控制方法的有效性。
非线性控制; 神经网络; 控制分配; 干扰项
0 引言
为了提高系统可靠性和容错性能,执行器冗余是一种被广泛采用的解决方案。近年来,在飞行器控制领域的高效控制执行器和故障容错方面,已取得较多的研究成果[1-3]。文献[2]提出了一种基于故障补偿控制律的故障容错方法。文献[3]利用最优控制分配方法提高了系统的容错性能。文献[4]提出基于控制分配的在线重构控制器,实现了故障容错。利用控制分配进行故障补偿时,不但保证了系统的容错性能,而且还不改变控制律。另外,实际应用系统常常受到外部干扰的影响,多表现为系统的非线性特性。文献[5]利用外部干扰观测器结合滑模控制来消除外部干扰。文献[6-7]利用智能控制方法处理系统的参数不确定性。文献[8-10]介绍了基于神经网络(RBFNN)的在线控制算法,提高了跟踪系统的局部特性。
以上方法主要是消除范数已知,或是消除线性时变的外界扰动对线性系统的影响。基于此,本文提出了一种自适应神经网络控制律,即建立在线调整神经网络参数的补偿算法,消除外部未知非线性干扰对系统的影响,从而保证了系统的鲁棒性。另外,结合控制分配实现了系统的故障补偿功能。
1 问题描述
考虑广义多输入多输出非线性纵向模型系统:

(1)
将模型进行线性化,得到如下形式的线性化模型:

(2)

假设1;矩阵对(A,B)可控。Rank(B)=q 假设2:未知外界扰动d(t)满足范数有界,即‖d(t)‖2≤α,但α未知。 (3) 式中:B=BvBu和Bv∈Rn×k均为列满秩矩阵;v=BuLu(t),v∈Rk为虚拟控制信号。 控制系统的结构如图1所示。该系统设计了控制律及参数更新律,保证了系统的鲁棒性,使误差系统渐进稳定。控制分配将虚拟控制信号分配到实际的良好执行器,使得系统在故障状态下仍然保持了良好的状态。 图1 控制系统结构图Fig.1 Structure diagram of control system 2.1 控制律与参数估计 神经网络鲁棒控制器的结构如图2所示,包括消除干扰的估计和反馈参数K的估计两部分。 设计的自适应控制律如下: (4) 图2 自适应神经网络控制器结构图Fig.2 ARBFNNC structure RBF神经网络包括输入层、隐藏层和输出层,本文的RBFNN的节点数分别为:2,7,1。总存在理想权重矩阵W*,满足: (5) (6) 式中:非线性高斯函数S(x)由基函数的si(x)组成(i = 1,2,…,n) : 式中:ci和σi分别为中心向量和带宽向量。 由式(2)~式(6)可得: (7) 设计在线自适应神经网络参数更新律为: (8) (9) 式中:Ξ为任意常数矩阵。总是存在理想常数阵K*和对称正定矩阵PT=P>0满足: (10) 为了消除神经网络的近似ζ(x)误差对系统的影响,设计滑模虚拟控制律: (11) 证明:选取Lyapunov函数 则V(t)对时间的导数为: 通过监测分析石化企业中一台驱动离心压缩机组的汽轮机,设计工作转速6 500r/min,一阶临界转速:4 020r/min,二阶临界转速:8 150r/min,多块可倾滑动轴瓦,迷宫密封,入口蒸汽压力:3.8MPa,出口蒸汽压力:0.008MPa,振动报警值—峰峰值38μm,振动停机值-峰峰值65μm。 2.2 控制分配律设计 将虚拟的控制输入指令v(t)分配给实际的控制输入u(t) : (12) 式中:Bx=BuL。由式(12)设计控制分配律: (13) 根据式(12),控制输入发生饱和后的控制分配最优解为: (14) 由式(13)和式(14),可得控制输入误差为: (15) (16) 那么系统的控制输入误差eu最终一致有界,即eu∈L2。 证明:选取Lyapunov函数 (17) 根据式(16),V1(t)对时间的导数为: (18) 另外,也可以得出:当执行器发生失效故障时,即Li≠1,控制分配律可以在线调节重新分配执行器,从而保证系统良好的控制性能。 结合定理1,系统在引入控制分配律后,控制系统仍然稳定,即具有良好的鲁棒性和故障补偿性能。 本文采用ADMIRE飞行器模型,飞行条件为Ma=0.22,H=3 km。状态矩阵和输入矩阵分别为: 当系统加入外部干扰,即d(t)=[0.1 sin 0.2t,0.5 cos 0.2t,0.02 sin 0.5t,0.2 cos 0.2t,5 sin 0.1t]T, 执行器无故障时,状态响应仿真结果如图3所示。可以看出,系统状态能够迅速镇定,保证了系统的鲁棒性。 图3 系统状态响应Fig.3 System state responses 在同样的外部干扰下,执行器控制效率失效40%时,或者飞行器中的左鸭翼失效10%,右鸭翼卡死,右内部升降副翼失效20%,方向舵卡死时,状态响应仿真结果如图4和图5所示。可以看出,虽然性能有所下降,但是系统状态最终仍然能够稳定。 图4 控制效率失效40%的状态响应Fig.4 State responses for loss of 40% control effectiveness 图5 执行器失效和卡死的状态响应Fig.5 State responses with actuator stuck-faults 由以上仿真验证可以看出,带有神经网络鲁棒控制器的闭环系统,在受到外部非线性时变干扰的情况下和执行器故障时,仍然一致渐进稳定。 本文针对一类有界干扰和执行器故障系统,采用神经网络的自适应控制算法与控制分配相结合的控制方案,很好地解决了飞机在受到外部干扰和执行器出现故障下的控制问题,其优势在于将自适应控制律与控制分配器独立设计。以ADMIRE模型为例,利用自适应神经网络控制算法近似有界未知的干扰项,加入负反馈消除了干扰因素对系统的影响,保证了系统的鲁棒性。控制律的输出作为分配器的输入,无需重构控制律,独立设计自适应控制分配器重新分配良好的执行器来补偿执行器失效和卡死的故障。仿真结果表明,该方法能够保证系统的鲁棒性,并有效解决故障情况下的控制分配问题,保证系统快速镇定,从而保持了飞行器较好的操纵品质。 [1] Chen W,Jiang J.Fault-tolerant control against stuck actuator faults[J].Control Theory and Applications,2005,152(2):138-146. [2] Dobre C.A cluster-enhance fault tolerant Peer-to-Peer system[J].International Journal of Innovative Computing,2014,10(2):417-436. [3] Liu Yu,Crespo L G.Adaptive control allocation in the presence of actuator failures[R].AIAA-2010-7772,2010. [4] Schwager M,Annaswamy A M,Lavretsky E.Adaptation-based reconfiguration in the presence of actuator failures and saturating[J].American Control Conference,2005,4(4):2640-2645. [5] Ginoya D,Shendge P D,Phadke S B.Sliding mode control for mismatched uncertain systems using an extended disturbance observer[J].IEEE Transactions on Industrial Electronics,2014,61(4):1983-1992. [6] Raimundez J C,Camano J L,Baltar J A.MIMO output feedback adaptive neural network control of an autonomous scale model helicopter mounted in a 2DOF platform[C]∥Automatic Congress,2004.Proceeding World.IEEE,2004:215-222. [7] Martens D.Neural network as a tool for the assessment of human pilot behavior in wind shear[J].Aerospace Science and Technology,1999,3(1):39-48. [8] Lei X,Lu P.The adaptive radial basis function neural network for small rotary-wing unmanned aircraft[J].IEEE Transactions on Industrial Electronics,2014,61(9):4808-4815. [9] Enns R,Si J.Helicopter trimming and tracking control using direct neural dynamic programming[J].IEEE Transactions on Neural Networks,2003,14 (4):929-939. [10] Tee K P,Gee S S,Tay F E H.Adaptive neural network control for helicopters in vertical flight[J].IEEE Transactions on Control Systems Technology,2008,16(4):753-762. (编辑:崔立峰) Robust adaptive neural network control with disturbances and actuator failures WANG Li1,2, LIU Chun-sheng1 (1.College of Automation Engineering, NUAA, Nanjing 210016, China;2.Jincheng College, NUAA, Nanjing 211156, China) A novel nonlinear adaptive control scheme is proposed for an over-actuated control system with unknown external disturbance and actuator failure. Through the reconstructed directly neural network,the parameter updating laws are used for providing automatic disturbance rejection ability in real time,it improves the robustness of system. Adaptive control allocation effectively compensates actuator failures or avoids the input saturation to improve the stability and maneuver. The sufficient conditions of stability are derived from Lyapunov arguments. Simulation results show the effectiveness and feasibility of the approach. nonlinear control; neural network; control allocation; disturbance 2016-09-02; 2016-10-25; 时间:2016-10-26 08:40 国家自然科学基金资助(61074063) 王丽(1977-),女,山东青岛人,讲师,博士研究生,研究方向为智能控制方法研究。 V249.1; TP183 A 1002-0853(2017)01-0030-04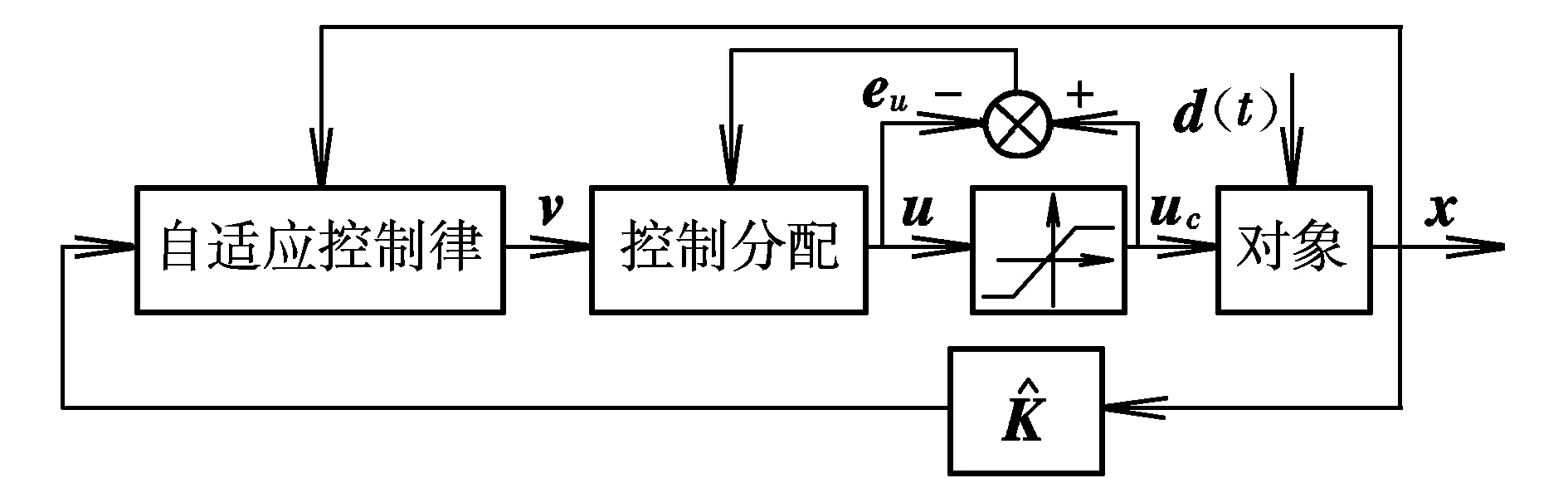
2 控制器设计


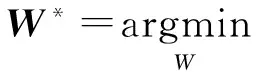


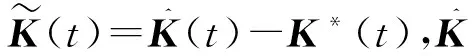



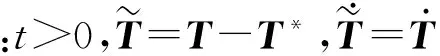



3 仿真验证





4 结束语

