机动飞行数值模拟关键技术及初步验证

李 立

(西安航空计算技术研究所 第七研究室, 陕西 西安 710068)

机动飞行数值模拟关键技术及初步验证

李 立

(西安航空计算技术研究所 第七研究室, 陕西 西安 710068)

建立飞机机动飞行仿真及飞行性能评估能力是未来航空CFD发展的重要目标之一,为此,对机动飞行数值模拟的方法、原理、关键技术及潜在的应用方向进行了探讨。采用惯性系下任意拉格朗日-欧拉 (ALE)形式描述的Navier-Stokes方程与机体运动学方程相耦合的方法,结合动网格技术建立了通用的机动飞行数值模拟应用框架。从微分方程形式的运动学方程出发,建立了与流动控制方程进行紧耦合和松耦合计算的两套计算方案,并提出了利用预报-校正技术提高耦合计算精度的方法。计算结果表明,所提方案合理、可行,为单自由度/多自由度机动飞行模拟、动导数分析等计算提供了可靠的新工具。

机动飞行; 动导数; 惯性系; 非惯性系; 计算流体力学

0 引言

机动性是评价现代航空武器装备性能优劣的重要指标。如第四代战机设计明确要求满足高机动飞行要求,而第五代战机设计要求进一步提升以满足超机动飞行要求[1]。这表明,对飞行器机动飞行及其气动特性的数值模拟将成为未来航空CFD应用的重要方向。广义的机动飞行可以定义为飞行状态(包括飞行速度、高度和方向)随时间变化的飞行,比如飞行表演中歼击机做出的各种机动飞行动作(盘旋、横滚、“眼睛蛇”等)。可见,机动飞行数值模拟显然是非定常的,必须采用基于非定常计算的手段才可能得到相对准确的计算结果。这也给算法的构建及具体计算带来实际困难,包括时间求解方面要有足够的精度,并且由于采用非定常计算迭代,计算时间较长。

本文主要对机动飞行数值模拟的方法、原理、关键技术及具体解决途径进行了探讨,建立了一种机动飞行数值模拟方案,并进行了初步验证,为进一步深入开展相关问题的数值分析奠定了基础。

1 总体技术思路

按照机动飞行的定义,要对机动飞行进行数值模拟,必须首先解决飞行状态的定义问题。具体包括3个要素:飞行速度、高度和方向。其中,飞行高度决定了计算中使用的当地气流条件,与飞行器本身的受力状态无关,在一定条件下可以忽略;而飞行速度、飞行方向是模拟中需要密切注意的关键量,与飞行器的受力状态直接相关。在飞行器飞行中,主要受力包括飞行器自身的重力、飞行器飞行中产生的气动力,以及基于飞行控制律施加的外力。这些合力直接决定了飞行器的飞行状态。由此不难分析,机动飞行模拟中,飞行状态的定义问题最终可归结为飞行器的机体运动学方程的建立问题。其次是机动飞行条件下流动控制方程如何建立的问题,即如何将传统的、在静态情况下建立的Euler或Navier-Stokes方程推广到能够处理机体运动的情况。此外,为了实现具体问题的分析求解,还必须解决上述两类方程如何耦合进行数值求解的问题。

2 关键技术及方案

2.1 机体运动学方程的建立

飞行器飞行状态可通过机体运动学方程来描述:描述飞行速度的方程对应了机体质心的运动学方程,即平动方程;描述飞行方向的方程对应了机体姿态变化的运动学方程,即转动方程。这两类方程均可通过3种方式建立,即解析方法、离散数据方法和动力学方程方法。其中:前两种方式本质上属于强迫运动形式,即飞行器飞行状态随时间的变化关系预先明确给定,计算中只关心机动飞行中飞行器气动特性的变化,不再考虑飞行轨迹的模拟及如何具体实现的问题;第三种方式可看作自由运动形式,即飞行器飞行状态随时间的变化关系需要以数值求解的方式,通过与流动控制方程耦合求解得到,同时,计算中需要考虑飞行控制律及飞行中各操纵面的影响。

在自由运动形式下,飞行器的飞行状态随时间的变化关系可由六自由度方程给出[2]。描述质心位移的平动方程和飞行姿态变化的转动方程分别为:

(1)

(2)

其中:

式中:T为姿态角变化率与体轴系下角速度之间的转换矩阵;Fouter,Mouter分别为合外力及合外力矩;m,I分别为飞行器机体的质量和转动惯量张量。

上述方程根据实际情况,还可只考虑平动或转动,从而形成三自由度方程。

2.2 流动控制方程的建立

在机动飞行模拟中,流动控制方程的建立可以采用两种思路。一种是在绝对坐标系(惯性系)下建立方程,这时求解的流体动力学方程为常规Euler/Navier-Stokes方程,同时考虑机体运动对流体的影响。其优点是流动控制方程的公式表达简单,可在现有求解器上直接开发,只需要在通量计算和边界处理中计及网格运动速度影响;缺点是必须显式进行网格运动,因而必须引入动网格技术来实现完整的求解过程。另一种思路是在相对坐标系(非惯性系)下建立方程,这时求解的流体力学方程是关于流体相对运动速度的方程,机体运动的影响通过控制方程的源项来体现。其优点是不需要显式进行动网格,因而不需要使用动网格技术,所有计算均在同一计算网格下进行;缺点是公式推导非常复杂,流场(在惯性系下)的动态变化过程必须通过对计算结果的后处理来完成。

本文选择第一种思路。在这种情况下,计算中计算域与机体一起运动,机体运动对流体的影响体现为网格运动带来的几何守恒律问题。基于几何守恒律,不难推导得到采用任意欧拉-拉格朗日(ALE)形式统一描述的Euler/Navier-Stokes方程:

(4)

其中,守恒变量及对流通量项的形式为:

(5)

(6)

式中:U,at分别为流体的相对速度及网格运动的法向速度,定义U=(u-xt,v-yt,w-zt),at=xtnx+ytny+ztnz。

当网格运动速度为0时,上述方程就是常规的Euler/Navier-Stokes方程。

2.3 运动学方程与流动控制方程的耦合

由ALE描述的Euler/Navier-Stokes方程(4),采用有限体积法可得其半离散形式为:

(7)

在惯性系下,网格运动速度根据

可得:

(8)

这样,式(7)和式(8)连同运动学方程式(1)和式(2)就构成了机动飞行模拟实际需要联立求解的方程组。该方程组是一个关于时间微分的常微分方程组,可采用松耦合或紧耦合的策略进行求解。松耦合方法是在同一时间步内独立求解流体力学方程和运动学方程,但按同一物理时间步推进更新流动控制变量及运动学参数。紧耦合方法是在同一时间步上,联立求解流动控制方程和运动学方程。理论上,紧耦合方法稳定性优于松耦合方法,但具体实践表明,两种方式的计算效果相当。松耦合方法的优势是可独立形成求解模块,便于编程及程序移植。本文采用松耦合方法。

3 具体方案及验证

整体采用松耦合求解思路,在同一物理时间步实现两者的耦合,利用预报-校正的技巧提高整体耦合求解的计算精度。流动控制方程求解基于结构网格有限体积法,采用时-空分开的半离散形式,空间离散采用3阶迎风偏置AUSM+格式(基于MUSCL插值和Albada限制器实现),时间推进采用τ-TS双时间步方法实现非定常计算。其中,物理时间计算采用二阶精度的后向差分法;虚拟时间计算采用LU-SGS格式。运动学方程求解通过独立模块实现,基于统一策略采用4级Runge-Kutta方法求解,并采用预报-校正技巧及“小窗口”技术提高整体耦合的物理时间计算精度[3]。

3.1 运动学方程求解验证

为了对运动学方程求解模块进行验证,采用两个具有解析解的典型算例进行了计算。一个是自由落体算例,用于验证平动方程求解的计算精度;另一个是自激振荡算例,用于验证转动方程求解的计算精度[4]。算例参数均进行了无量化处理。

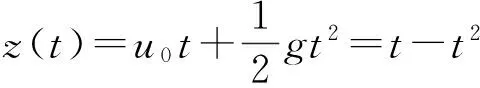
自激振荡算例中,假设机体不受任何外力和外力矩的作用,初始速度为u0=(0,0,0)；初始转速为ω0=(1.0,0.0,0.5),对应的解析解为ωx=a× cos(λt),ωy=bsin(λt),ωz=c,其中,a=1,b=-1,c=0.5,λ=0.25。

图1给出了不同时间步长得到的数值解与解析解的比较。可以看出,本文运动学方程求解程序稳定性非常好,对不同时间步长都有很好的适应性。

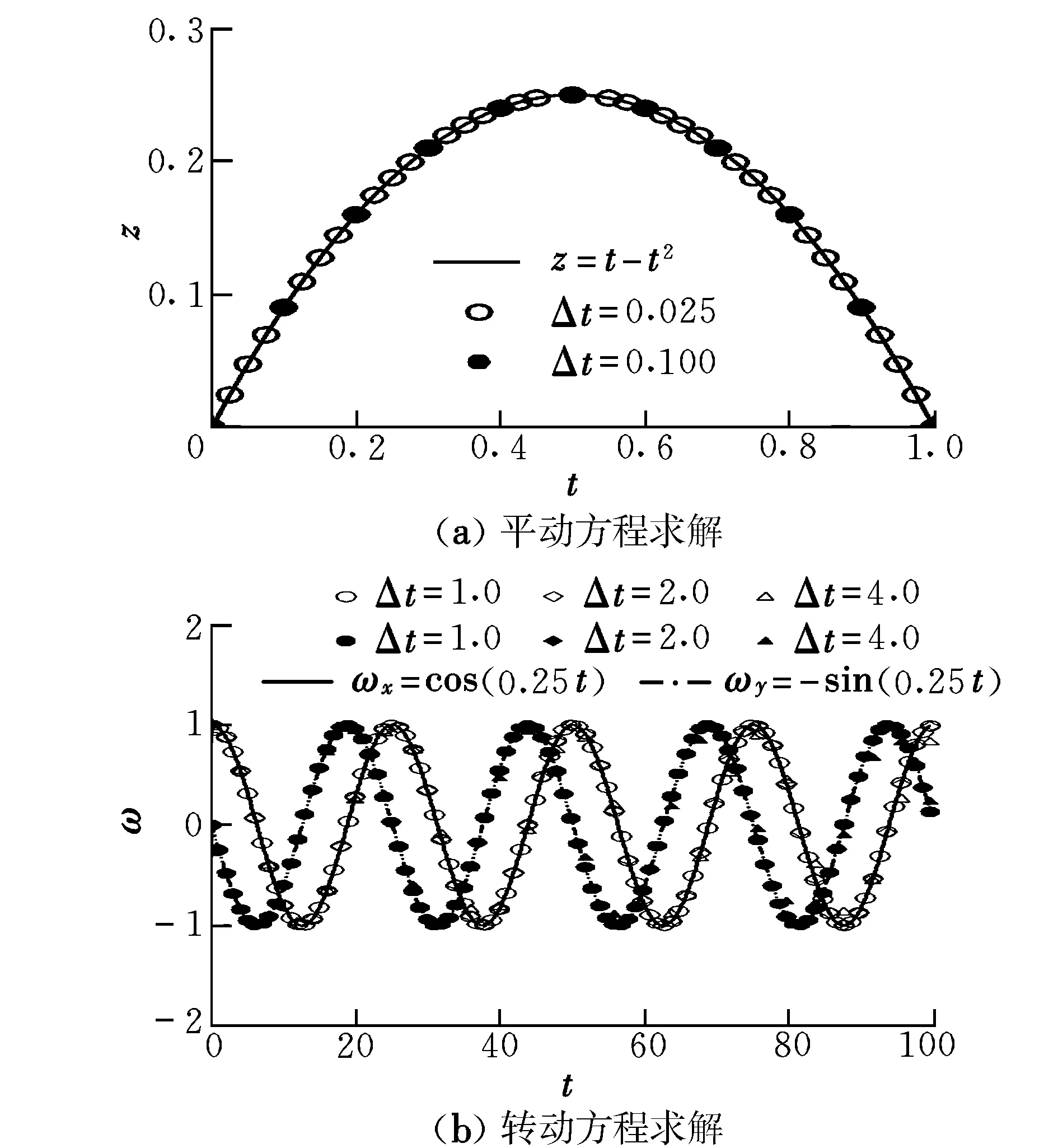
图1 运动学方程求解验证结果Fig.1 Validation results for solving the kinetic equation

3.2 强迫运动及动导数算例计算

与常规强迫运动采用解析形式或离散数据形式给出不同,这里,强迫运动采用等价的微分方程形式给出,以便考核运动学方程与流动控制方程耦合求解的能力,采用NACA0012俯仰振荡算例[5]和高超声速动导数计算标模HBS算例。俯仰振荡解析表达式θ=α+Δθsin(2πft)的等价微分形式可写为:

(9)

这样,通过联立流动控制方程、式(9)和角位移方程即可实现俯仰振荡计算。图2给出了NACA0012翼型典型结果。选取的计算状态为:Ma=0.6,α=2.89°,Re=4.8×106,并取式(9)中Δθ=1.41°,f=50.32 Hz,t无量纲。

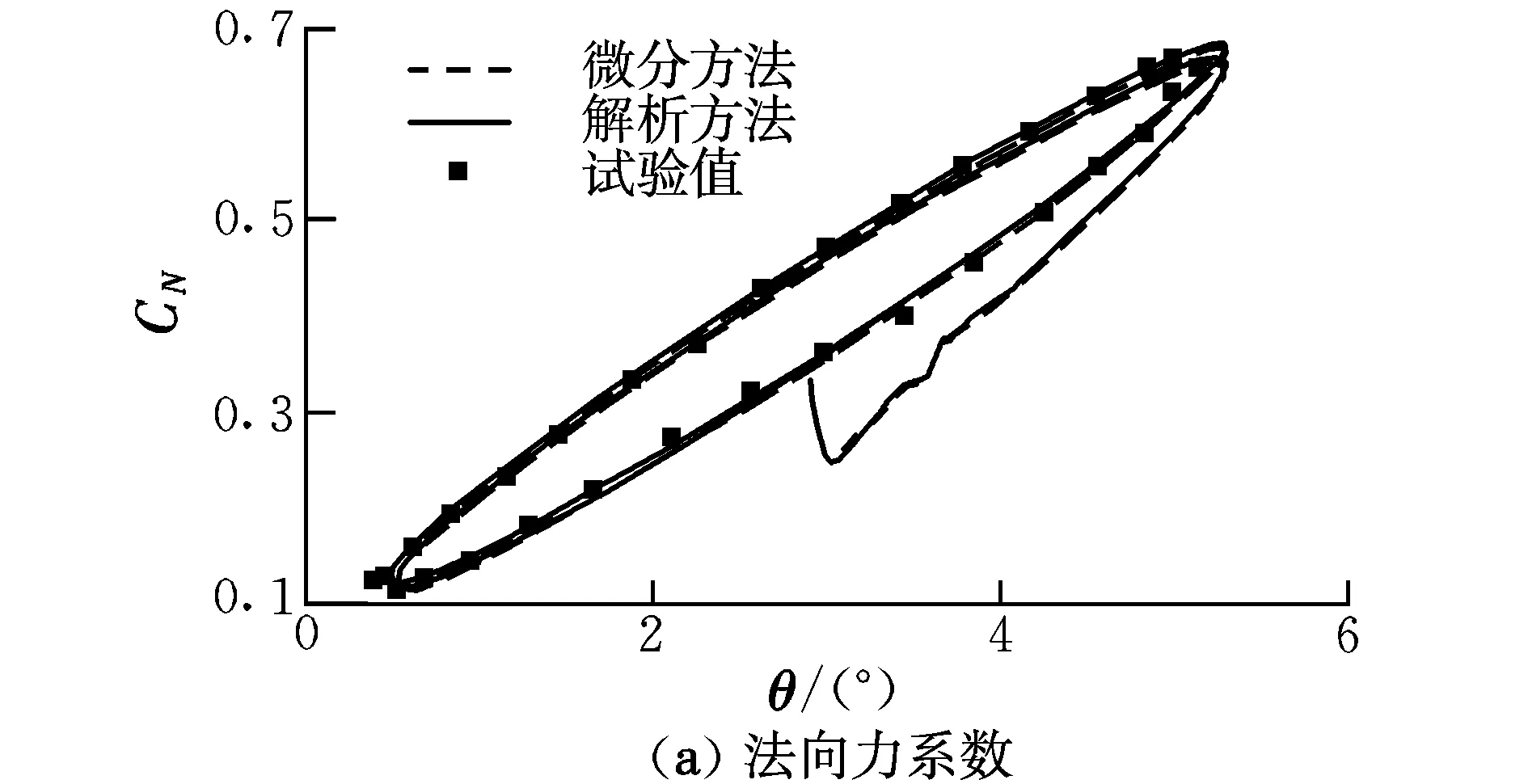
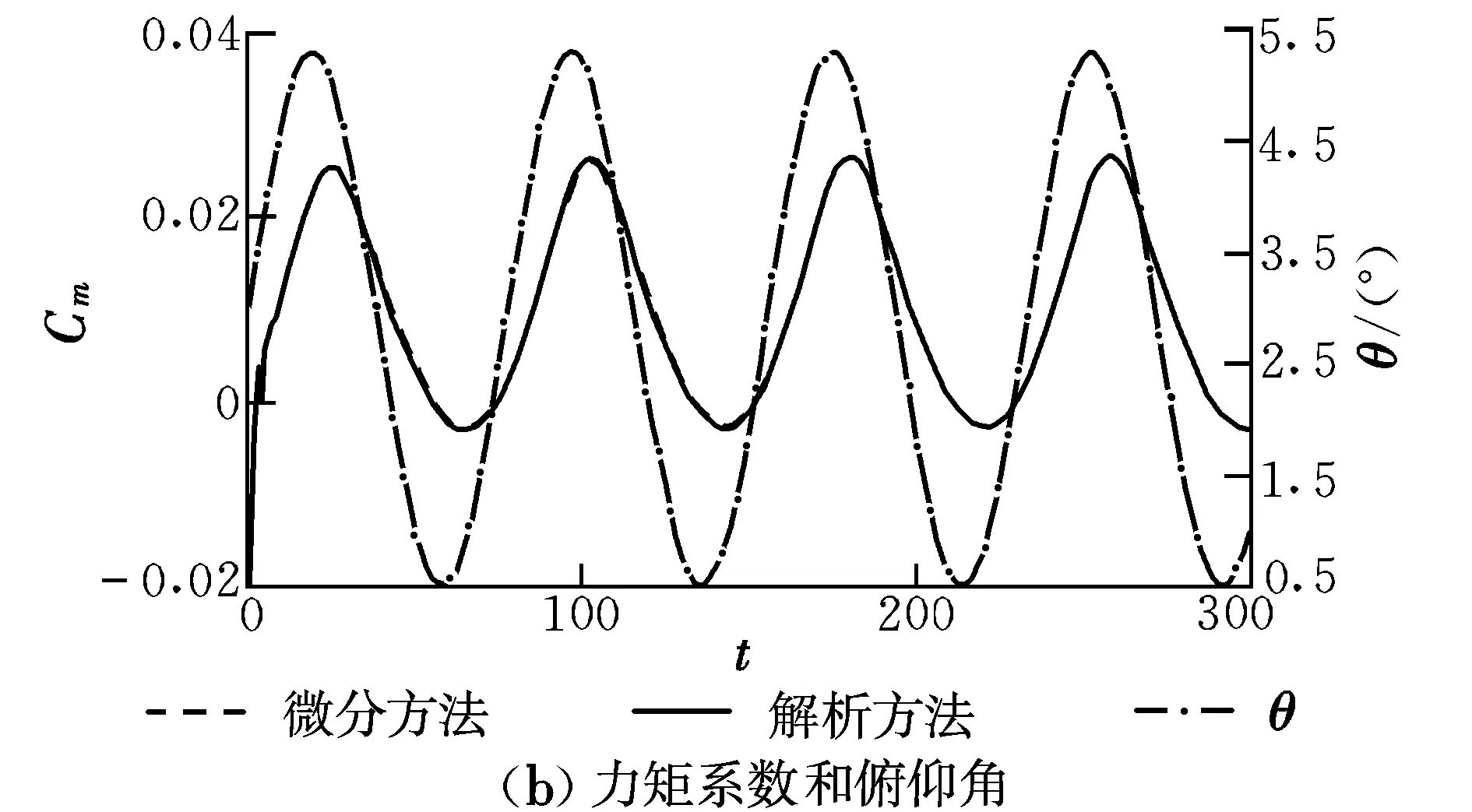
图2 NACA0012俯仰振荡算例计算结果Fig.2 Typical results for pitching NACA0012 airfoil

由图2可以看出,采用解析形式与本文采用微分方程形式得到的结果一致,表明本文运动学方程与流动控制方程耦合求解的程序实现完全正确。

图3给出了采用类似方法得到的高超声速弹体外形(HBS)算例的静导数和动导数计算结果,来流条件为:Ma=6.85,α=0°～15°。其中,动导数的后处理分析采用积分法、最小二乘法、T-F方法等多种方法作为对比。可以看出,几种处理方法得到的结果一致,并与试验值和理论值符合良好,获得了预期的计算效果。

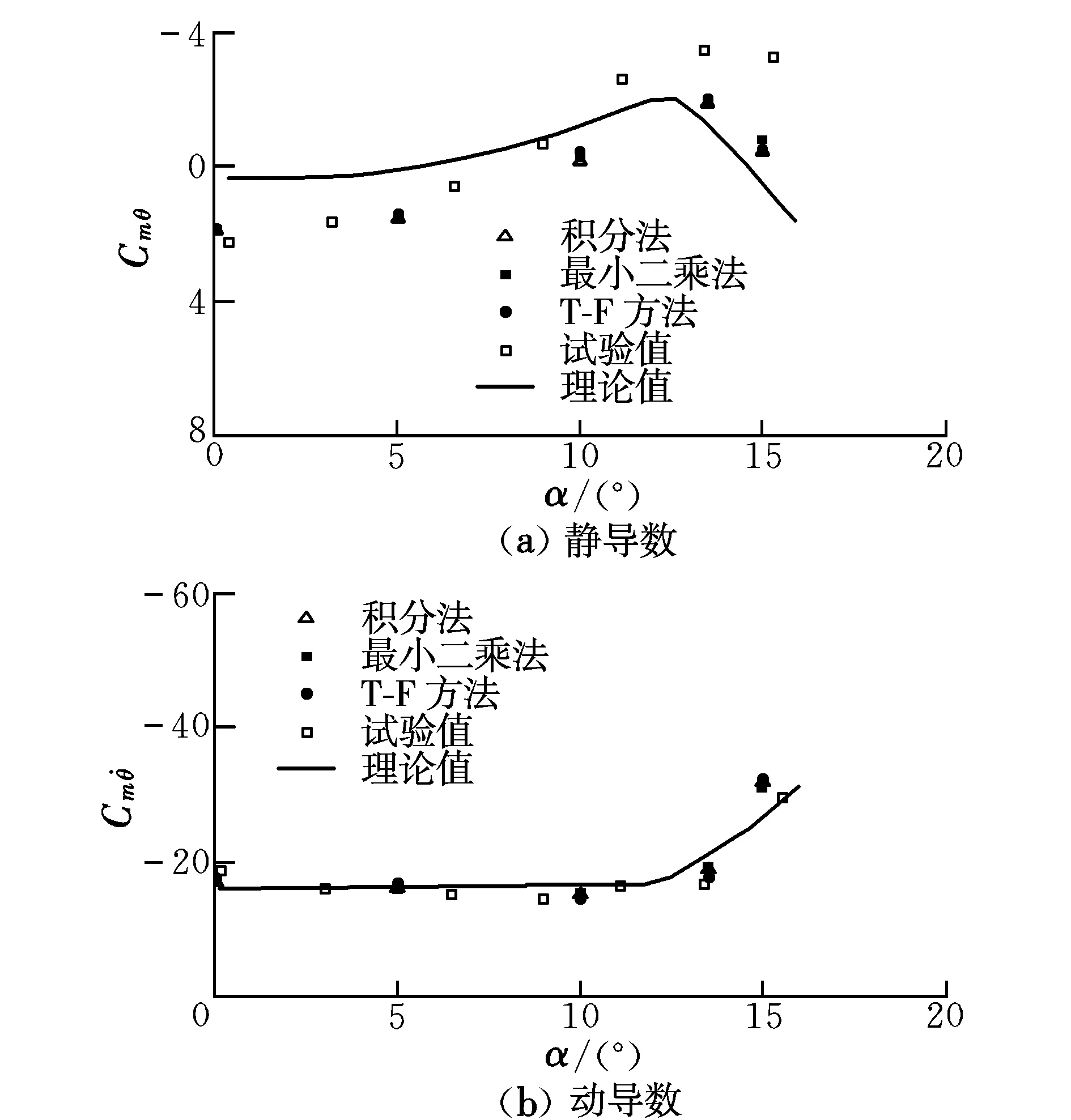
图3 HBS静导数和动导数算例计算结果Fig.3 Results for static and dynamic derivatives of HBS

3.3 自由运动算例计算

为了对程序在自由运动情况下的机动飞行模拟能力进行验证,选择NACA0012翼型进行自由振荡计算。这类计算的实际应用包括通过计算寻找配平迎角的计算等。具体选择Ma=0.8,α0=0°和Ma=0.8,α0=1.25°两个状态开展计算,t无量纲。模拟场景为翼型固定在0.25c位置,在气动力矩作用下逐渐平衡。图4给出了计算得到的迎角及升力系数随时间的变化历程。可以看出,两个计算条件下得到的配平状态基本一致,结果合理。

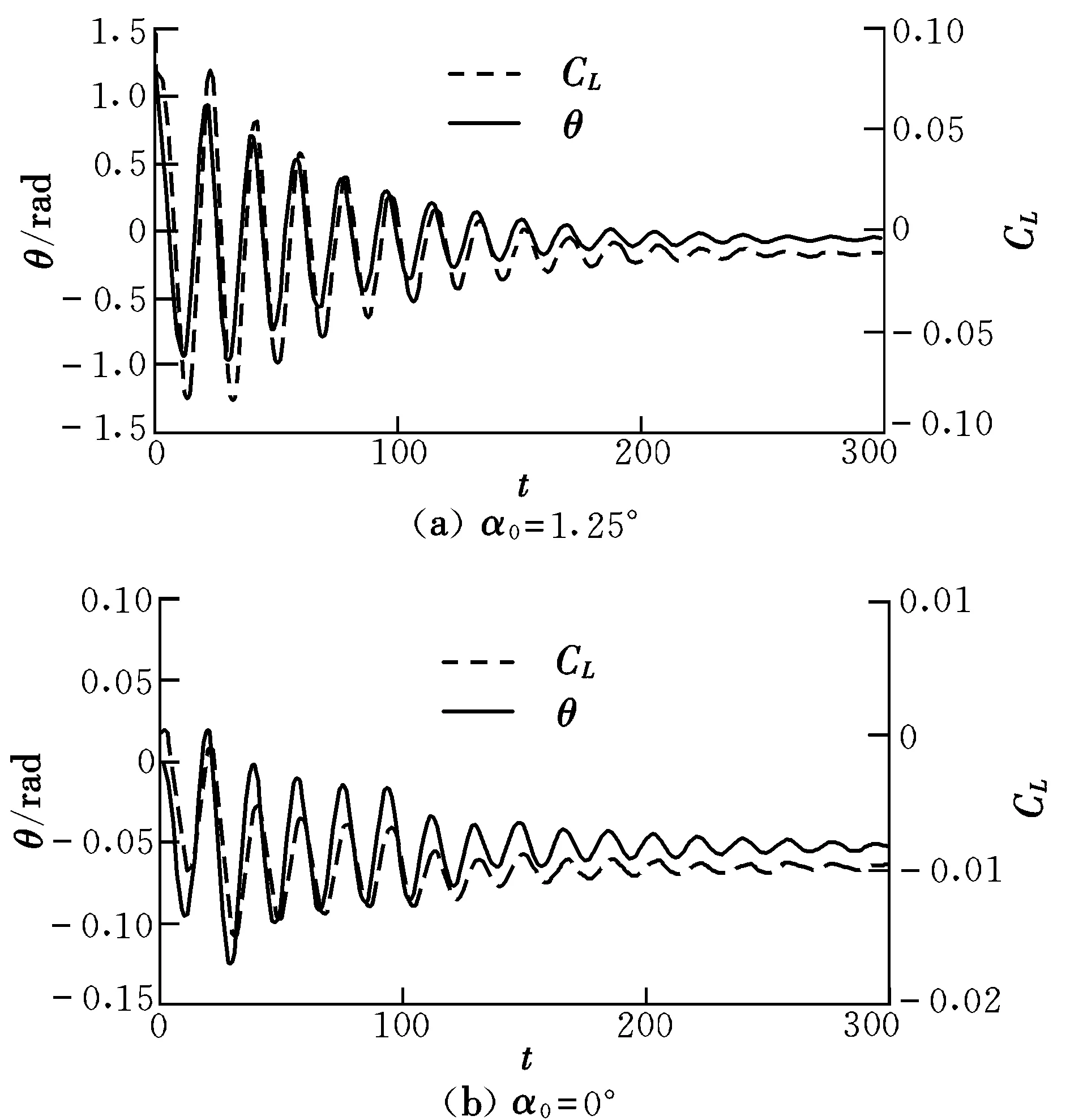
图4 NACA0012自由振荡算例计算结果Fig.4 Calculation results for free oscillating NACA0012 airfoil

4 结束语

本文对飞行器(飞机、导弹)机动数值模拟的相关关键技术进行了研究,发展了一套开放的机动飞行数值模拟计算框架,并通过典型算例进行了程序验证,得到了合理的计算结果,表明上述方案合理、可行,有望为单自由度/多自由度机动飞行模拟、动导数计算提供可靠的新工具。下一步有必要进一步开展上述程序的工程验证及复杂工程应用。同时,在该程序基础上,研制在非惯性系下的机动飞行模拟程序,主要难点包括:推导非惯性系下基于相对运动速度描述的流动控制方程的一般形式;等效源项的隐式处理;计算结果后处理等。

[1] 高劲松,陈哨东.国外六代机发展情况研究[J].飞航导弹,2014(1):54-59.

[2] 肖业伦.飞行器运动方程[M].北京:航空工业出版社,1987:21-24.

[3] 邓建中,葛仁杰,程正兴.计算方法[M].西安:西安交通大学出版社,1985:269-270.

[4] Murman S M,Aftosmis M J.Simulations of 6-DOF motion with a cartesian method[J].AIAA-2003-1246,2003.

[5] Landon R H.NACA0012 oscillating and transient pitch,compendium of unsteady aerodynamic measurements[R].AGARD-R-702,1982.

(编辑：李怡)

Key technologies and preliminary validation for numerical simulation of maneuver flight

LI Li

(Seventh Department, ACTRI, Xi’an 710068, China)

Establishing the capability of flight simulation and flight performance estimation is one of the important goals for the future aviation CFD, some keynotes on numerical simulation of maneuvering flight with its methodologies, principles, key technologies and potential applications were discussed. Combined with moving grid techniques, an open framework for simulation of maneuvering flight was established based on the Navier-Stokes equation in arbitrary Lagrange-Euler (ALE) formulation coupled with the kinematic equation for aircraft. Based on kinematics equation in the form of differential equation, two numerical schemes to loose coupling and tight coupling with flow control equation were built, and a predictor-corrector method was further proposed to increase the prediction accuracy. Numerical results show that the schemes are reasonable and feasible, which can be used as a new robust tool for simulation of single or multiple freedom degree maneuver, prediction of dynamic derivatives.

maneuvering flight; dynamic derivative; inertial frame; non-inertial frame; CFD

2016-06-08;

2016-10-27;

时间:2016-11-10 09:10

国家863计划资助项目(2012AA01A304)；航空科学基金资助(2015ZA31002)

李立(1977-)，四川成都人，高级工程师，硕士，研究方向为计算流体力学。

V211.3

A

1002-0853(2017)01-0089-04