刍议摆钟走时快慢的相对误差
宋辉武
(鄂尔多斯市第一中学 内蒙古 鄂尔多斯 017010)
赵林明
(广东实验中学 广东 广州 510375)
刍议摆钟走时快慢的相对误差
宋辉武
(鄂尔多斯市第一中学 内蒙古 鄂尔多斯 017010)
赵林明
(广东实验中学 广东 广州 510375)
从物理学角度探究了不准确摆钟走时的相对误差,并通过举例分析用相对误差的两种表达式解题时所带来的差别,期望可以澄清广大教师对这一问题的误解.
摆钟 相对误差 准确度
摆钟问题历来是高中物理的一个难点,很多教师曾在各大刊物发表过大量的论文,但是对于其中的一个问题(即不准确摆钟走时的相对误差问题)似乎大部分教师都非常容易走进误区.由于这一问题具有一定难度,因此并不要求学生掌握,也正因为如此,很多人也就不太注意,但是如果将这个错误观点带进课堂,学生利用这一结论直接解题将会出现严重的错误.笔者深入研读了近几十年的大量文献,发现很多文献都在这个问题上犯错,而由于问题的隐蔽性极高,再加上大多数人的思维定势导致这一错误并没有被人发现,下面笔者将通过其中一篇典型的文章展开讨论,进而澄清这一问题.
1 问题的提出
问题:走时准确的摆钟的周期为T准,走时不准确的摆钟的周期为T不准,问走时不准确的摆钟的相对误差为多少?

这一观点在有的刊物上得到公开发表,其错误的隐蔽性可见一斑,鉴于此,笔者认为这一在教师中广为流传的错误观点亟待澄清.
文献[1]通过数学分析法得出摆钟问题的计算公式,其主要思路是先进行了一个假设
(1)

其中l为摆长,并利用这个错误公式计算了几道例题.
读罢文献[1]收获颇多,尤其被作者扎实的数学功底所折服,由于文献[1]是完全通过数学途径得出的结论,因此顺着其思路根本不会发现文章中的任何错误,隐蔽性极高,而笔者也是从物理学的角度进行对照时才发现其错误所在.
2 问题分析
问题剖析:值得注意的是,严格地讲,摆钟并不是单摆,而是复摆(即刚体绕定轴旋转的物理摆),引入等值摆长后可视为单摆.根据摆钟的机械构造,不论走时准确的钟还是不准确的钟,只要摆钟的摆完成了一次全振动,钟面指针摆过的角度都是相同的,比如说秒针都跳动了1 s,因此走得快的摆钟,其实际周期短,走得慢的摆钟,其实际周期长.其中主要涉及两类摆钟问题,摆长发生变化引起的以及重力加速度发生变化引起的计时不准确问题.下面我们针对慢钟和快钟从物理学角度进行讨论.
2.1 慢钟走时的相对误差
假设不准确的慢钟在时间t内其钟面显示的时间为t′,其周期为T慢,准确摆钟的周期为T准,不难理解T慢>T准,则不准确的慢钟在时间t内摆动的次数为
因此,不准确的摆钟其钟面显示的时间
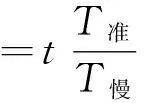
不准确的慢钟走时的相对误差为
2.2 快钟走时的相对误差
假设不准确的快钟在时间t内其钟面显示的时间为t′,其周期为T快,准确摆钟的周期为T准,不难理解T快 因此,不准确的快钟其钟面显示的时间 不准确的快钟走时的相对误差为 2.3 摆钟走时快慢的相对误差 由此可知不准确摆钟走时的相对误差为 (2) 反过来我们可以看出文献[1]中的错误出现在源头的假设上,实际上假设式(1)应该由 (3) 替代才能得出正确结论. 而对于文献[1]中给出的例题来说,其解析过程也是错误的. 【例1】某摆钟当摆长调到30.00 cm时,12 h内慢了150.0 s,试问当摆长调到29.50 cm时,在一昼夜内摆钟是快了还是慢了多少时间? 原文错解:已知 由摆长调整公式可得 当摆长为29.50 cm时,由同一公式求出 由于k′是负值,故可知摆钟又走快了,由 Δt′=k′t′=0.004 9×86 400 s≈ 423.4 s≈7.06 min 正确解析:由式(2)可得 因此 l准=30.00×(1-0.003 5)2cm≈29.79 cm 当摆长为29.50 cm时,根据 即可解得 86 400×0.004 9 s≈423.4 s≈7.06 min 【例2】如果摆长为l1的摆钟在一段时间里快了n秒,摆长为l2的摆钟在相同时间里慢了n秒,则准确摆钟的摆长应为多少? 典型错解:根据 对于走时慢的钟有 即 (4) 对于走时快的钟有 即 (5) 联立式(4)、(5)即可解得 正确解析:根据式(2),对于走时慢的钟有 即 (6) 对于走时快的钟有 即 (7) 联立式(6)、(7)即可解得 1 查裕康.摆钟问题的计算公式.物理教师,2004(4):54~55 2016-03-20)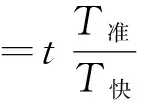
3 例题分析
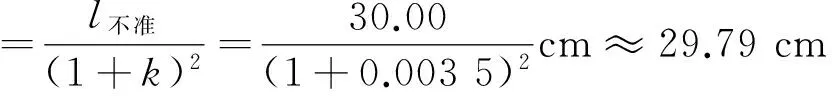
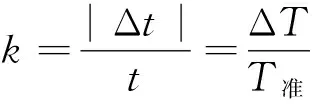
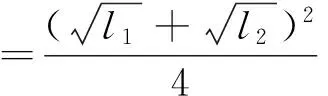

4 结束语

