水中直尺像上刻度线的疏密变化研究
董芳芳
(盐城市亭湖高级中学 江苏 盐城 224000)

水中直尺像上刻度线的疏密变化研究
董芳芳
(盐城市亭湖高级中学 江苏 盐城 224000)
由于存在像散,水中放置直尺所成虚像的清晰度将受到破坏.直尺所成虚像一般呈弧形,像上刻度线的疏密程度随之发生相应变化.数值计算结果表明,像上刻度线的疏密程度随观察位置变化而变化,在同一位置观察时像上各部分刻度线的疏密程度也有所不同.一般地,像上刻度线较原尺变密,而在特定情形下,像上刻度线有可能较原尺变疏.
折射 虚像 刻度线 几何光学
现将一把直尺放入水中,观察者在水面上方不同位置观察水中直尺所成虚像,为简单起见,不妨假设直尺、直尺入水点处的法线以及眼睛共面,如图1所示,显然,由于存在像散直尺所成虚像的清晰度将受到一定程度的破坏.但直尺所成虚像上刻度线的密度将发生什么变化?是变疏了还是变密了?
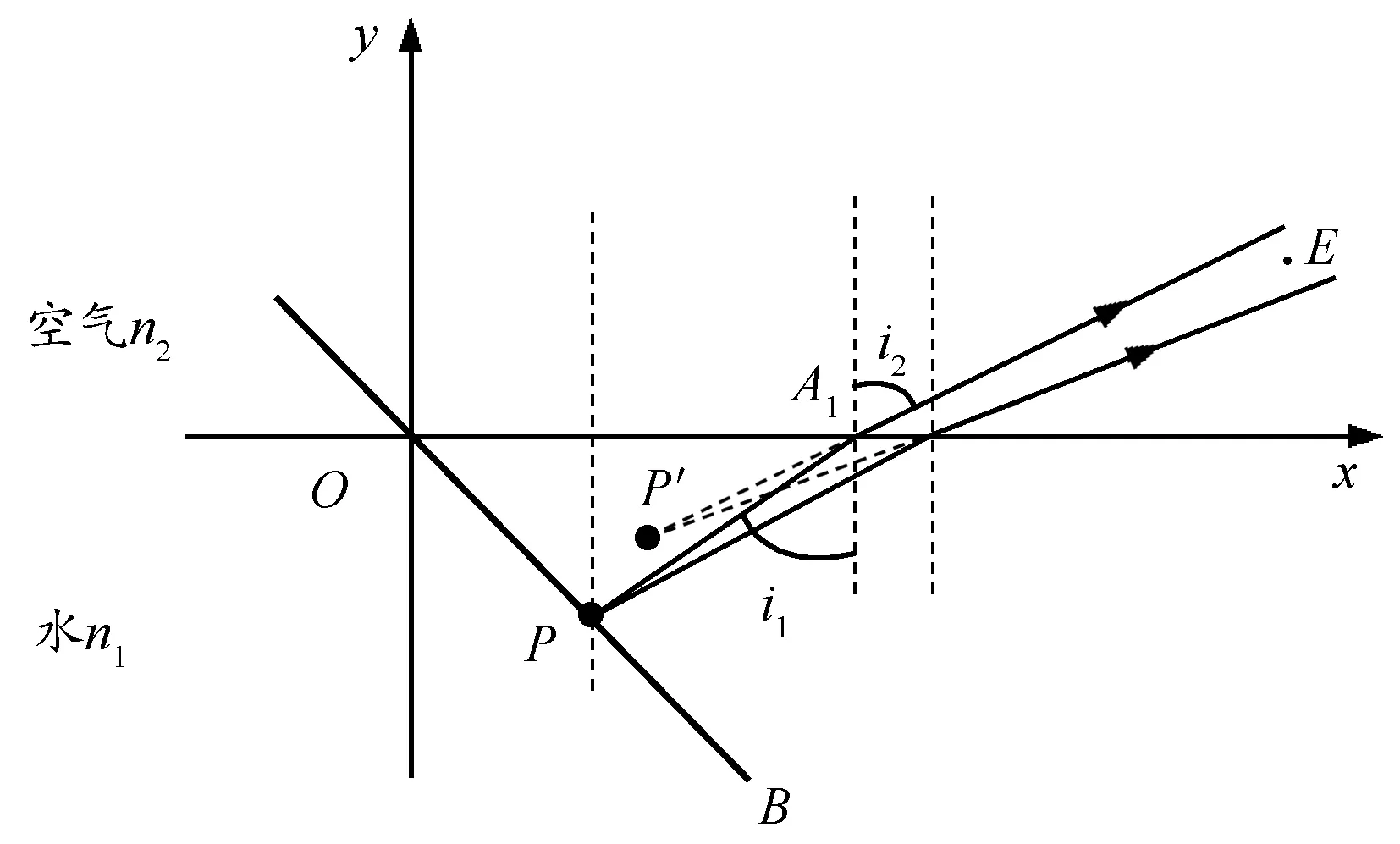
图1 水下直尺成像光路图
在图1中,人眼处于水面上方并在直尺右侧的E点处,其坐标设为E(xE,yE),直尺OB倾斜放置时所处直线的方程设为y=kx,其中k为斜率(当直尺OB竖直放置时k=∞).考虑水下直尺上任意一点P(xP,yP)发出的两条相互靠得极近的光线经折射所成的虚像为P′(xP′,yP′),入射光线PA1与法线的夹角为入射角i1,相应的折射角为i2.虚像P′的坐标经计算可得[1]
(1)
可见,虚像P′的坐标满足方程
其中入射角i1满足下列关系
(2)
其中n1为水的相对折射率,n2为空气的相对折射率.本文将采用数值计算的方法给出人眼观察到水下直尺所成虚像的位置.不妨取水的相对折射率为n1=1.3,空气的相对折射率n2=1,在计算中取直尺倾斜放置时斜率k=-1,直尺水下部分的长度OB=0.2 m,人眼所处E点的坐标分别为(0.3,0.2),(0.4,0.2),(0.5,0.2)(单位:m),则所观察到的虚像的位置分别如图2中B,C,D3条曲线所示,直线A表示水下直尺的成像位置,可见人眼处于不同位置观察到的虚像的弯曲程度不同,同一虚像上各部分图像的斜率也不相同,以致水下直尺所成虚像上各部分刻度线的疏密程度也随之发生变化.
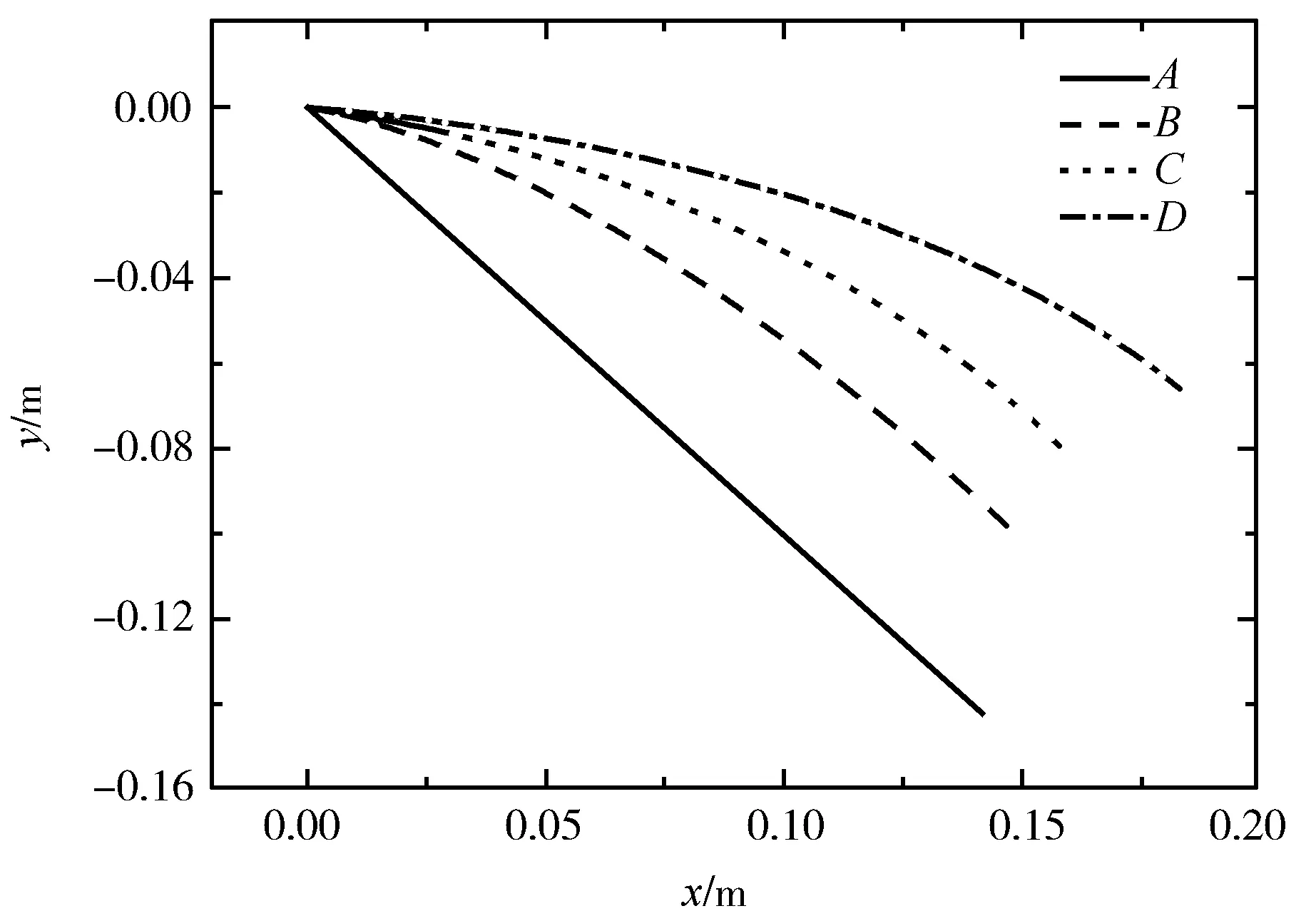
图2 人眼处于不同位置观察到水下倾斜放置直尺所成虚像位置
为比较虚像上刻度线的疏密变化程度,我们将直尺水下部分从O点到B点等分为40段,并分别标为第1~40段,每段的长度为5 mm.图3中,人眼所处E点的坐标分别为(0.3,0.2),(0.4,0.2),(0.5,0.2)(单位:m)时观察所得各等分段虚像所对应长度与尺上原长的比值如图3中B,C,D3条曲线所示,直线A为比值为1的参考线.由图3可以看出,如果直尺足够长,那么直尺水下部分接近水面的地方虚像各段的长度相对于原尺上各等分段的长度变长,沿着直尺向下虚像各段的长度逐渐减小,直至小于直尺等分段的长度,然后逐渐增加.即相对于原尺上的刻度线而言,斜率k=-1的水下直尺所成虚像上的刻度线从入水点开始先变疏,再逐渐变密,但尺的下端稠密程度或有所减小.
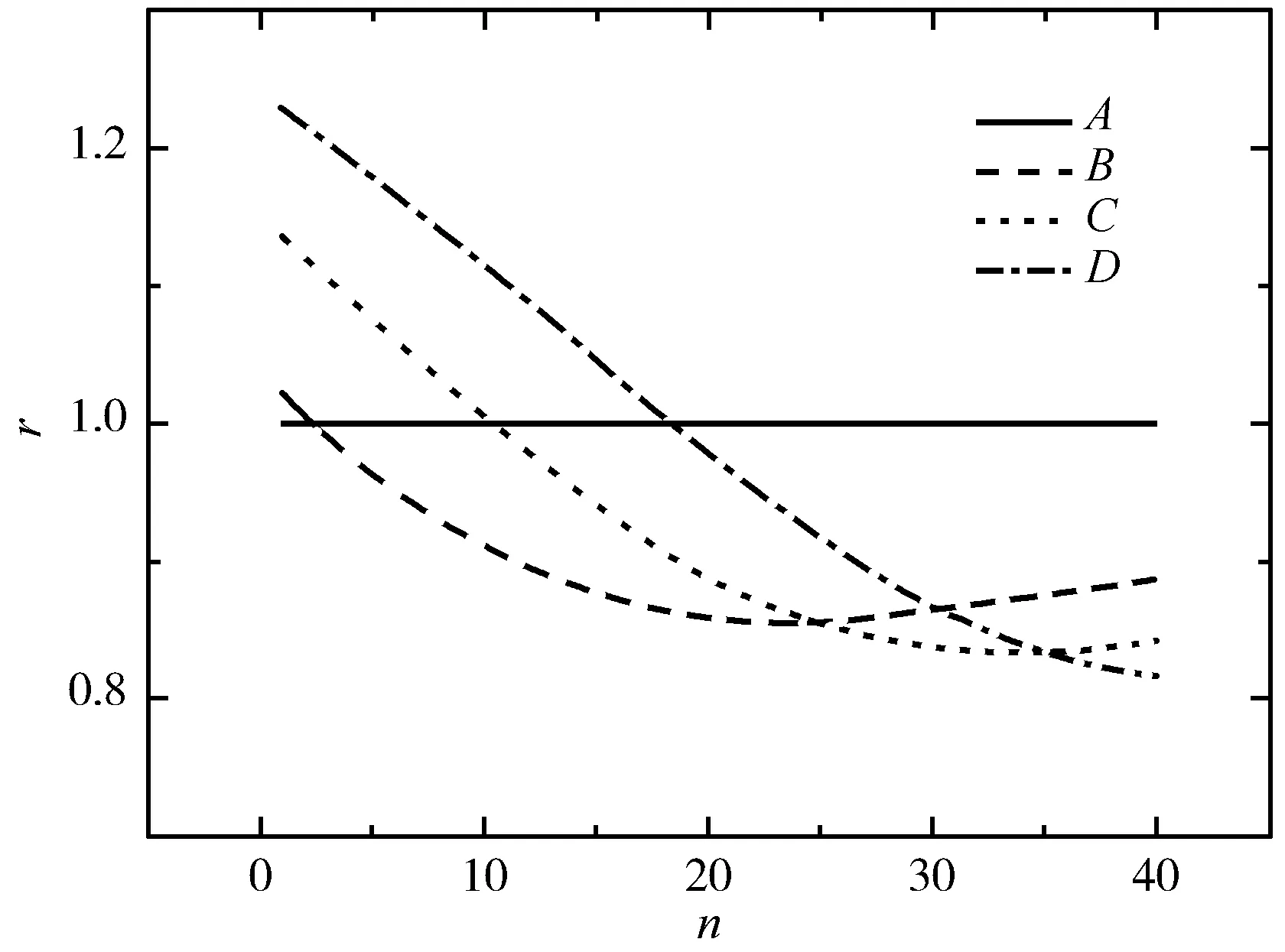
图3 人眼处于不同位置观察到水下倾斜放置直尺各等分段所成虚像长度与原长之比
作为对比,我们还给出了水下直尺竖直放置时人眼处在不同位置观察到的虚像位置以及所成虚像上刻度线疏密变化情况,分别如图4和图5所示.
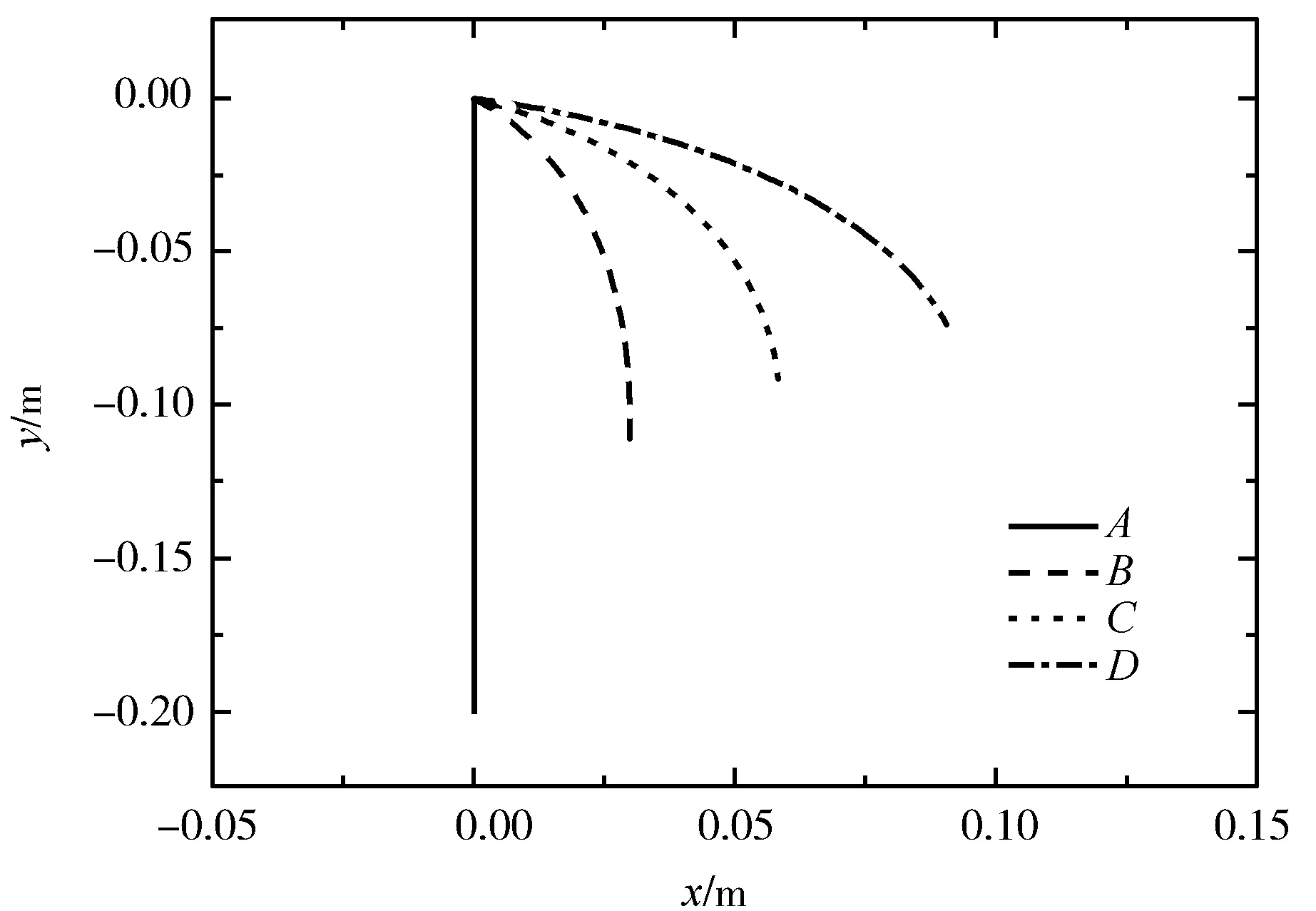
图4 人眼处于不同位置观察到水下竖直放置直尺所成虚像位置
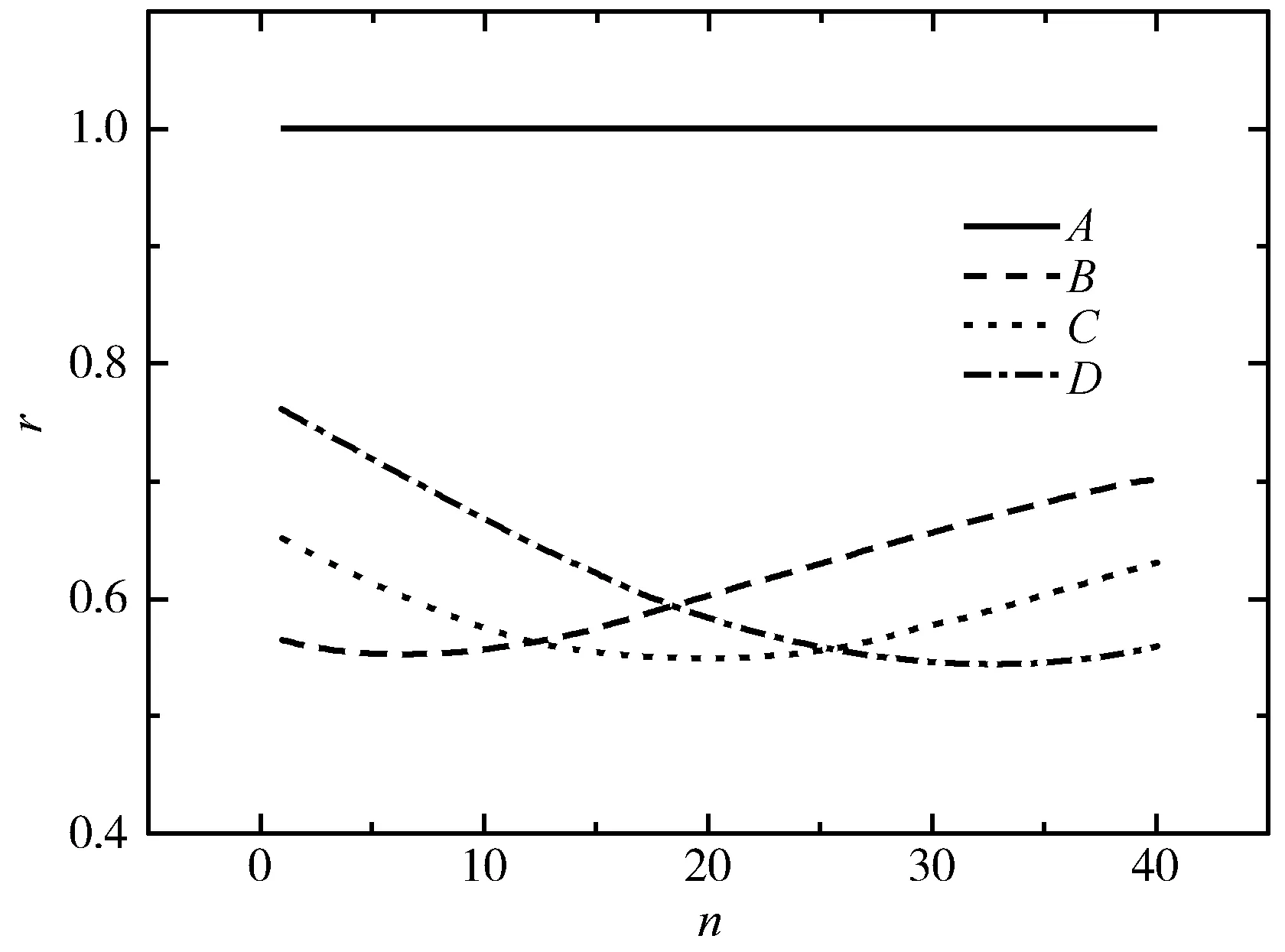
图5 人眼处于不同位置观察到水下倾斜放置直尺各等分段所成虚像长度与原长之比
在图4中,人眼所处E点的坐标分别为(0.3,0.2),(0.4,0.2),(0.5,0.2)(单位:m)时,观察到的虚像的位置分别如图中B,C,D3条曲线所示,图中A表示水下直尺的成像位置.同样,人眼处于不同位置观察到的虚像的弯曲程度不同,同一虚像上各部分刻度线的疏密程度也随之发生变化.在图5中,人眼所处E点的坐标分别为(0.3,0.2),(0.4,0.2),(0.5,0.2)(单位:m),观察到各等分段虚像所对应长度与原长之比如图5中B,C,D3条曲线所示,直线A为比值为1的参考线.可见当原尺水下部分足够长时,相对于原尺上刻度线,水下直尺竖直放置时所成虚像上的刻度线从入水点开始逐渐变密,但靠近尺的下端稠密程度或有所减小.
总之,相对于原尺上刻度线而言,人眼处于同一位置观察到的水下直尺上刻度线的密度有可能变疏,也有可能变密;眼睛处于不同位置观察到水下直尺的像的弯曲程度不同,像上各处刻度线的密度也有所不同.
1 姚启钧. 光学教程.北京:高等教育出版社,2002.160~161
StudyontheChangesofScaleMarkDensityonaRulerImageunderWater
DongFangfang
(TinghuSeniorHighSchool,Yancheng,Jiangsu224000)
The clarity of the virtual image of a ruler underwater reduces due to the astigmatism. The virtual image of the ruler bends to some degree, and the scale mark density of the image changes. The calculation shows that the scale mark density of the image changes with the position of the observer. Even when the observer is at the same position, the scale mark density of the different parts of the ruler is somewhat different. The scale mark density of the image may be greater or smaller than the original density.
refraction; virtual image; scale mark; geometrical optics
董芳芳(1987- ),女,硕士,中教一级,主要从事中学物理教学.
2016-08-02)

