黏性土边坡上条形基础安全距离分析

赵志峰，韦张林

(南京林业大学土木工程学院，南京210037)

黏性土边坡上条形基础安全距离分析

赵志峰，韦张林

(南京林业大学土木工程学院，南京210037)

在边坡上修建建筑物时，基础距坡顶的水平距离将直接影响到建筑物和边坡的稳定性，而目前缺乏合理确定基础距坡顶安全距离的方法。采用数值方法建立了不排水条件下黏性土坡上条形基础的计算模型，通过与经典文献中的计算结果对比验证了数值计算的可行性，然后通过数值计算得到的承载力系数变化趋势来确定安全距离。在大量数值分析的基础上，研究了土体强度、土体重度、基础宽度、边坡坡角等因素对于安全距离的影响。结果表明：土体的归一化抗剪强度对于边坡破坏模式以及基础的安全距离都有较大的影响；当边坡较陡尤其是抗剪强度较低时，基础距坡顶的安全距离明显增大；当坡高大于一定值后对于基础承载力系数的影响可忽略不计。通过结果整理，得到了不同情况下的安全距离的建议取值，为实际工程中确定建筑物在坡上的位置提供参考。

黏性土坡；条形基础；安全距离；数值分析

我国地势辽阔、分布着大量的山区和林区，由于地形起伏大，这些地区的发展建设常会面临建设用地的问题。根据地形地貌，在山地边坡上修建各类建筑物是合理利用土地资源的一种有效方式[1]。但不同于平地，在坡上修建建筑物必须考虑边坡稳定的影响。如果距坡顶过近，建筑物所产生的荷载会增加边坡失稳的风险，从而使建筑物的整体安全面临巨大威胁。因此，在坡上修建建筑物时必须合理控制基础距坡顶的水平距离。

目前关于边坡稳定的分析方法和平地上基础承载力的确定方法都比较成熟，但关于坡上基础对边坡稳定和地基承载力影响的研究相对较少[2-4]。Hansen是较早研究坡上基础承载力的学者，并给出了承载力系数的确定公式；Vesic在此基础上对公式进行了修正。他们提出的方法未考虑土坡的重度，且认为基础位于坡顶，与实际情况不符[5]。Michalowski[6]利用极限分析给出了坡上基础的上限承载力的理论解。Bowles[7]给出了确定坡上基础距坡顶合理距离的经验公式，但公式中并未考虑坡高和土体参数的影响。Georgiadis[8]分析了位于坡顶的条形基础在轴心及偏心荷载下的承载力。这些研究基本都是研究不同情况下坡顶基础的承载力，对于基础距坡顶的安全距离并未涉及。

我国《建筑地基基础设计规范》规定：位于稳定边坡上的基础，当基础底面边长不超过3 m时，其基础底面外边缘线至坡顶的水平距离应符合下式要求，且不小于2.5 m：

a≥ξb-d/tanβ

(1)

式中：β为土坡坡角(°)；d为基础埋深,m；b为基础宽度,m；ξ为系数，取3.5(条形基础)或2.5(矩形和圆形基础)。

从图1可以看出，规范给出了坡上基础距坡顶水平距离的确定方法，公式(1)中考虑了坡角、基础宽度及埋深的影响，但未考虑边坡土体参数等因素的影响，存在不足。另外，规范的公式仅适用于坡角不超过45°的情况，对于较陡但土质较好的边坡并未给出确定方法。

图1 规范关于坡上基础安全距离的示意图Fig. 1 Diagrammatic sketch of foundation on the slope in national standards

基于目前缺乏合理确定坡上基础安全距离方法的这一现状，笔者采取数值分析的方法、在参考前人研究结果的基础上，充分考虑影响因素，对黏性土边坡坡上基础的安全距离进行了全面分析，旨在总结出合理的确定方法，为实际工程提供参考。

1 数值模型的建立及验证

1.1 基本模型

由于实际情况下，黏性土边坡的数量更多，所以本试验研究黏性土边坡上条形基础的安全距离。建立的几何模型如图2所示，其中：条形基础的宽度为B，其外边缘距坡顶的水平距离用λB表示。λ为本试验所研究的相对安全距离，当基础距坡顶的距离达到λB时，基础的承载力几乎不受边坡存在的影响。作用在基底上的极限荷载为qu；边坡的坡角为β，坡高为h。土体采用经典的莫尔库伦模型，建模时所需的黏性土的参数有：土的抗剪强度、重度和压缩模量。由于黏性土的渗透系数低，所以抗剪强度取不排水强度cu；土的重度和压缩模量对于土坡稳定和地基承载力的影响很小，所以两个指标取为定值(γ取20 kN/m3，Es取30 MPa)。模型两侧施加水平约束，底面施加全约束[9]。

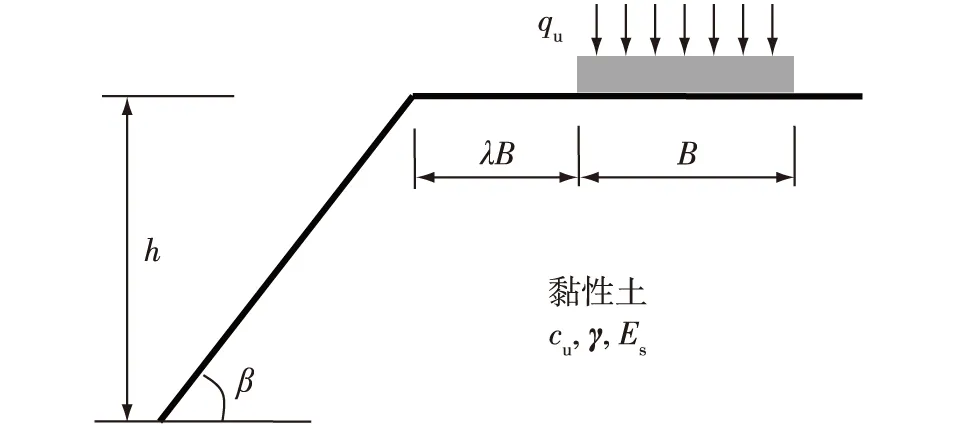
图2 几何模型示意图Fig. 2 Diagrammatic sketch of geometric model

根据理论分析和前人的研究结论，影响坡上基础稳定性的主要因素是坡角β、基础距坡顶距离λB、黏性土不排水强度cu和坡高h。由于当坡高大于某定值后，对结果没有影响(后文中将提到)，所以在初步分析中取h=3B(基础宽度B取3 m)。主要影响因素的取值范围为：

β取30°，45°，60°，75°，90°；λ取0，1.0，1.5，2.0，2.5，3.0，3.5，4.0，5.0；cu取30，60，120，180，300 kPa。

1.2 数值计算验证

为了验证数值计算的可靠性，与经典文献中关于类似问题的计算结果进行了比较。Georgiadis[5]在2010年针对坡上基础的承载力系数进行了一系列数值模拟计算：将有限元的模拟结果与现有方法进行比较，以验证数值计算结果的正确性。

不排水条件下条形基础的极限承载力可如下表示[10]：

qu=cuNc

(2)

式中：Nc为无量纲承载力系数，其数值可直接反映承载力的大小，其变化趋势可反映安全距离的取值。

图3为本研究有限元数值模拟(FE)结果同Georgiadis计算结果的对比。从图中可知：在坡角取不同值(30°，45°，60°)时，随着相对距离λ的增加，承载力系数Nc逐渐增加；当λ大于一定值后，Nc保持不变，等同于平地时的承载力系数，说明此时边坡的存在对基础已经没有影响，达到了安全距离。数值计算结果非常接近，说明了本研究计算的可靠性。存在少许误差的原因可能是由于网格疏密度以及计算过程中收敛准则的影响。

图3 数值计算结果对比验证Fig. 3 Comparison and verification of numerical computation results

图6 不同λ时β对Nc的影响Fig. 6 The influence of β on Nc with different λ

2 安全距离的影响因素分析

2.1 黏性土抗剪强度的影响

本次研究中通过一个无量纲归一化强度cu/(γB)来反映不排水强度的影响，原因是：①无量纲的强度参数便于讨论和应用，这也是国外学者广泛采用的表达形式[11-12]；②已有研究表明虽然cu、γ、B都会对Nc值有影响，但当cu/(γB)的比值相同时，可以得到大致相同的Nc值。

由于篇幅原因，只列举λ取0和5时，cu/(γB)对Nc的影响(图4)。从图中可知，cu/(γB)对Nc的影响很小(但对承载力qu有直接影响，qu=Nccu)，仅在β改变的情况下，Nc值才发生变化。且当λ较大时(λ=5)，不同坡角时的承载力系数趋于一致。

值得注意的是，计算中发现cu/(γB)的数值虽然对Nc几乎没有影响，但是会影响坡上基础的失稳模式。图5为不同坡角时cu/(γB)对坡上基础承载力的影响。当cu/(γB)小于一定数值时，承载力qu的数值迅速下降，说明此时破坏模式发生了变化，即从地基承载力破坏转化为边坡整体失稳[13]。因为当抗剪强度过低时，边坡本身就很难维持稳定。所以存在一个临界值cu/(γB)crit：当cu/(γB) >cu/(γB)crit时，可以将建筑物基础修建在边坡上；若cu/(γB)

图4 cu/(γB)对Nc的影响Fig. 4 The influence of cu/(γB) on Nc

图5 cu/(γB)对失稳模式的影响Fig. 5 The influence of cu/(γB) on the mode of instability

2.2 坡角β的影响

坡角越大、边坡越陡，对坡上基础的不利影响就越明显。当cu/(γB)=2或5时，承载力系数Nc均随着β的增加而减小。当基础位于坡顶(λ=0)时，这一趋势更加明显(图6)。

当基础离坡顶距离增大时(λ=3)，坡角对承载力系数Nc的影响明显降低：当cu/(γB)=2、坡角小于60°时的承载力系数完全相同，仅当坡角超过60°时，Nc才会有明显下降；而当cu/(γB)=5时，Nc仅有少量下降。当λ=5时，坡角对Nc几乎没有影响。这说明基础距坡顶越远，土坡对基础的影响越小，安全距离的数值与坡角、土的强度等因素有关。

2.3λ的影响

λ是表征基础外边缘至坡顶水平距离的参数，直接反映出安全距离的取值，其含义是相对安全距离[14-15]。图7为不同cu/(γB)数值、不同坡角β时，λ对Nc的影响。当cu/(γB)=1时，β和λ对Nc的影响十分明显。当λ取较大值(>7)时，Nc才基本趋于稳定。

图7 λ对Nc的影响Fig. 7 The influence of λ on Nc

随着cu/(γB)数值的增加，土体的强度提高，边坡对基础的影响逐渐减弱，表现为Nc在λ取值较小时就趋于稳定。当cu/(γB)=2时，除β为90°外，Nc在λ=4时保持不变；而当cu/(γB)=5时，在不同坡角下，Nc在λ=3.5时保持不变。这也充分说明了安全距离的取值同多种影响因素相关，而且同很多因素呈现非线性变化的趋势。

2.4 埋深的影响

当基础埋置于地面以下时，埋深范围内的土体自重会抑制破坏面的发展而使得承载力有所提高。取基础的埋深d为1 m，模拟了不同强度、不同坡角的情况，并与无埋深(d=0 m)时进行对比。从图8可以看出，当土体强度较低时，不同坡角下有无埋深时的Nc曲线变化趋势相似，有埋深时的承载力略高于无埋深时。当土体强度较高时，有埋深时的承载力系数明显高于无埋深情况，但Nc都在λ=3时趋于稳定。模拟结果表明，埋深使承载力有所提高，但对相对安全距离并无实质的影响。所以不考虑基础埋深对于研究相对安全距离是可行的，且结果偏于安全。

图8 埋深对Nc的影响Fig. 8 The influence of foundation depth on Nc

3 结果与分析

由数值计算结果可见，坡上基础的承载力系数Nc受到多种因素的影响。当Nc下降时，说明基础的承载力降低，边坡对邻近的基础造成了影响[16]。当Nc趋于稳定时，表明边坡的存在对于基础几乎没有影响，可认为已达到安全距离。根据Nc的变化趋势整理出相对安全距离λ的结果如表1所示。

表1 相对安全距离λ结果

从表1可以看出，相对安全距离λ与归一化土体强度cu/(γB)和坡角β有关。随着坡角的增加，基础所需的安全距离逐渐增加；随着归一化强度的增加，安全距离逐渐减小。实际工程中黏性土坡上条形基础的安全距离可以参照表1取值(λB)。

4 结 论

1)目前缺乏黏性土坡上基础距坡顶水平距离的合理确定方法。本试验建立黏性土坡上的条形基础的数值模型，研究了不同情况下条形基础承载力系数的变化趋势，并确定出基础的安全距离。

2)土体强度与重度、基础宽度、坡角等因素对基础距坡顶的相对安全距离有着直接的影响。参数分析结果表明：①土体归一化强度cu/(γB)的大小会影响坡上基础的失稳模式，即存在一个临界值cu/(γB)crit，当cu/(γB)

[1]何思明, 张晓曦, 欧阳朝军. 条形基础荷载对边坡稳定性影响与加固研究[J]. 岩土工程学报, 2011, 33(12):1980-1986. HE S M, ZHANG X X, OUYANG C J. Influences of loads of stripe footing on slope stability and its reinforcement[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12):1980-1986.

[2]KESKIN M S, LAMAN M. Model studies of bearing capacity of strip footing on sand slope[J]. KSCE Journal of Civil Engineering, 2013, 17(4):699-711.

[3]酆庆增. 临近边坡的基础的极限承载力[J]. 上海力学, 1999, 20(1):24-27. FENG Q Z. Ultimate bearing capacity of the foundation near a slope[J]. Shanghai Journal of Mechanics, 1999, 20(1):24-27.

[4]HUANG C C, KANG W W. The effects of a setback on the bearing capacity of a surface footing near a slope[J]. Journal of GeoEngineering, 2008, 3(1):25-32.

[5]GEORGIADIS K. Undrained bearing capacity of strip footings on slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 136(5):677-685.

[6]MICHALOWSKI R L. Three-dimensional analysis of locally loaded slopes[J]. Geotechnique, 1989, 39(1):27-38.

[7]BOWLES J E. Foundation analysis and design[M]. 5th edition. New York: The McGraw-Hill Companies, Inc., 1996.

[8]GEORGIADIS K. The influence of load inclination on the undrained bearing capacity of strip footings on slopes[J]. Computers and Geotechnics, 2010, 37(3):311-322.

[9]赵志峰, 杨帆. 刚性下卧层对地基变形影响的计算方法[J]. 南京林业大学学报(自然科学版), 2014, 38(5):139-142. ZHAO Z F, YANG F. Convenient computation method of settlement considering the existence of rigid ground[J]. Journal of Nanjing Forestry University(Natural Sciences Edition), 2014, 38(5):139-142.

[10]卢廷浩. 土力学[M]. 北京: 高等教育出版社, 2010.

[11]KUSAKABE O, KIMURA T, YAMAGUCHI H. Bearing capacity of slopes under strip loads on the top surfaces[J]. Soils and Foundations, 1981, 21(4):29-40.

[12]TAIEBAT H A, CARTER J P. Bearing capacity of strip and circular foundations on undrained clay subjected to eccentric loads[J]. Geotechnique, 2002, 52(1):61-64.

[13]SHIAU J S, MERIFIELD R S, LYAMIN A V, et al. Undrained stability of footings on slopes[J]. International Journal of Geomechanics, 2011, 11(5):381-390.

[14]LESHCHINSKY B. Bearing capacity of footings placed adjacent toc′-φ′ slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(6):1-13.

[15]GEORGIADIS K. An upper-bound solution for the undrained bearing capacity of strip footings at the top of a slope[J]. Géotechnique, 2010, 60(10):801-806.

[16]KESKIN M S, LAMAN M. Model studies of bearing capacity of strip footing on sand slope[J]. KSCE Journal of Civil Engineering, 2013, 17(4):699-711.

Study on the safety distance of strip footing on cohesive soil slope

ZHAO Zhifeng，WEI Zhanglin

(SchoolofCivilEngineering,NanjingForestryUniversity,Nanjing210037,China)

The horizontal distance between the foundation and the top of the slope directly affect the stability of the slope and buildings. However, the reasonable method determining the safety distance from the foundation to the top of the slope is in deficiency at present. In this study, numerical simulation method is applied to analyze the factors which influence the safety distance and make parameter study. First, numerical models of strip footing on slope of cohesive soil under undrained condition are established and the feasibility of numerical simulation is verified by comparison with the results in the classic literature. Afterwards, the safe distance is determined through the change trend of the bearing capacity coefficient obtained by numerical calculation. On the basis of large quantity of numerical computation, the influences of several factors such as soil shear strength, soil unit weight, footing width, slope angle on the safety distance are studied. The simulation results indicated that the normalized shear strength of soil has remarkable influence on the failure mode on the slope and the safety distance. The safety distance increases significantly on the case of steep slope angle especially when the soil shear strength is low. The height of slope has negligible effect on the bearing capacity of footing and slope stability when the slope is higher than a certain value. The relative safety distance in different conditions is obtained through sorting out the simulation results, which can provide a reliable reference for determining the position of the strip footing on the slope in the practical projects.

cohesive soil slope; strip footing; safety distance; numerical analysis

2016-05-26

2016-11-03

国家自然科学基金青年项目(51508279)。

赵志峰，男，副教授，研究方向为地下工程、生物岩土。E-mail:zzf0911@163.com

TU433

A

2096-1359(2017)01-0130-05