基于振动信号残差法的齿轮故障诊断分析与仿真*
田原嫄,李超逸
(东北电力大学 机械工程学院,吉林 吉林 132012)
基于振动信号残差法的齿轮故障诊断分析与仿真*
田原嫄,李超逸
(东北电力大学 机械工程学院,吉林 吉林 132012)
为了防止齿轮故障,文章基于振动信号残差法,将采集的振动信号进行同步时域平均后,再将其进行快速傅里叶变换,将平均后的信号独立分离成两部分,从而得到齿轮的常规信号和故障信号。然后,再通过计算残差信号有效值,对故障变化程度给出定量描述。通过比较,可以明显看出时域图中信号波形无明显差异,而经处理后的残差图中常规振动信号幅度较小,波形中出现明显的峰值变化处,即故障信号,同时峰值越突出的地方即故障越严重的位置。
齿轮故障诊断;振动信号;残差法;同步时域平均法;MATLAB
0 引言
近年来随着风电机组的广泛使用,由齿轮箱故障或损坏引起的机组停运事件时有发生,由此带来严重的直接损失和间接损失,维修人员投入维修的工作量也不断增加。然而,齿轮是齿轮箱的重要组成部件之一,据有关资料统计,齿轮故障占旋转机械故障的10.3%[1]。为了保证齿轮箱平稳工作,防止振动和冲击,齿轮故障诊断与仿真工作逐渐成为风电设备领域的研究热点之一[2]。一般来说,齿轮振动信号中总是存在着很强的与故障无关的“常规振动”成分,而由于故障所造成的振动信号相对于“常规振动”来说总是很小的,因此,如果直接利用齿轮振动测量信号所得到的特征基数往往不够敏感,因此,本文采用振动信号残差分析法[3-4],将上述的两种成分分离开来,并独立分析“故障振动”部分信号,则可以提高诊断的识别精度。
1 振动信号残差法的齿轮故障诊断原理
残差分析方法的具体过程:先对同步时域平均后的信号进行快速傅里叶变换(FFT)滤波处理。从而分别得到齿轮的“常规振动”信号r(n)和“故障振动”信号d(n)。然后再通过计算残差信号有效值(RMS值)或峭度系数,从而对故障变化程度给出定量描述。常规振动经变化和反变换后差值较小。而故障振动信号经变换后与原来的信号差值较大。残差分析法的工作原理图,如图1所示,残差分析法的仿真分析流程图,如图2所示。
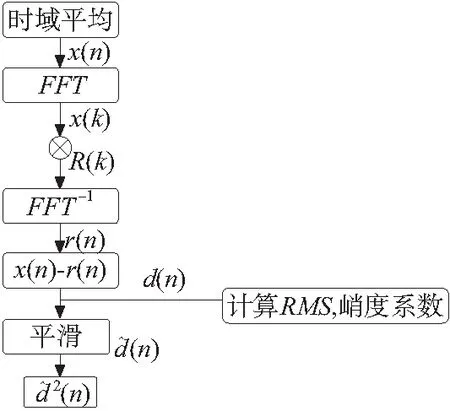
图1 振动信号残差法分析原理
1.1 时域同步平均法
从齿轮振动中取出啮合频率成份,将它同齿轮轴的旋转频率同步相加、平均,这种方法称作时域同步平均法[5]。由于齿轮由振动引起故障时导致异常啮合,冲击振动的振幅要比其它齿的大,所以时域平均信号曲线上幅值最大的峰值位置即是异常齿的位置,其分析原理如图3所示。

图2 残差分析法的仿真分析流程图
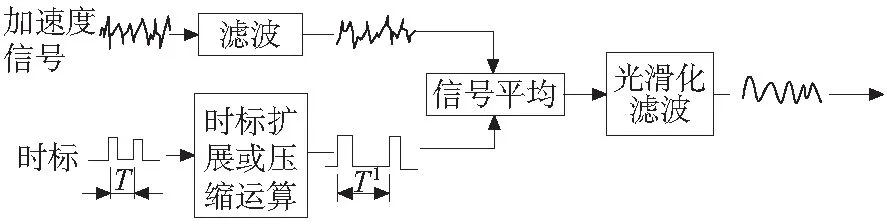
图3 同步时域平均法原理
本文基于Matlab处理振动特征信号时将仿真故障信号(如图4a所示)截取N段(如图4b所示),然后进行平均运算得到如图5所示的信号。
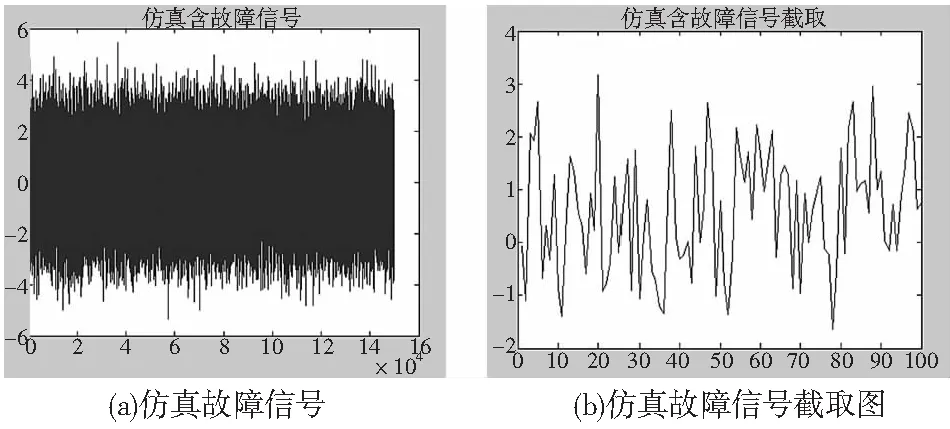
图4 仿真故障信号

图5 同步时域平均仿真波形图
1.2 快速傅里叶变换及反变换原理
快速傅里叶变换(FFT)是有限序列离散傅里叶变换的一种快速算法,该算法由Cooly 和Tukey[6](1965)提出。快速傅里叶变换的主要特点是大大地减少进行离散傅里叶变换所需要的运算次数。同时,由于运算次数的减少,从而减少了运算时间,提高了计算机的使用效率,使振动信号的实时处理得以实现。本文将采集到的信号分成N段,建立N点序列x(r),形成N点离散傅里叶变换可表示成[7]:

(1)
其中利用系数Wkr的周期性,即:
Wkγ=Wk(γ+N)=W(k+N)γ
(2)
可将离散傅里叶变换运算中的某项合并。利用其对称性,即:
Wkγ+N/2=-W
(3)
根据其周期性可将长序列的离散傅里叶变换分解成短序列的离散傅里叶变换。FFT算法基本上可以分为两大类:按时间抽取法和按频率抽取法。本文采用按时间抽取的FFT算法。
将N=2L的序列x(r)(r=0,1,3,...,N-1),先按r的奇偶分成两组:
x(2s)=x1(s)
x(2s+1)=x2(s)
(4)
分别求N/2点的离散傅里叶变换,得到前半部分:
X(k)=X1(k)+WkX2(k)(k=0,1,2,…,N/2-1)
(5)
后半部分为:
X(k+N/2)=X1(k)-WkX2(k)(k=0,1,2,…,N/2-1)
(6)
重复这一过程,可得到x(r)的FFT。快速傅里叶变换算法和快速傅里叶反变换的算法原理基本相同,逆变换公式为:

(7)
经过以上求算,获得残差图(如图6所示),并截取部分残差图(如图7所示)。
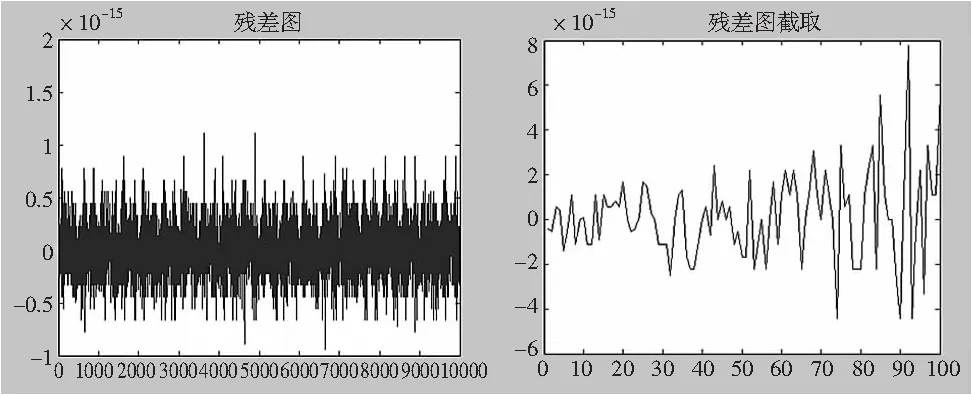
图6 残差图 图7 残差截取图
经图5的仿真模拟信号截取的信号时域波形图和图7残差截取图的比较,可以明显看出时域图中信号波形无明显差异,而经处理后的残差图中常规振动信号幅度较小,而波形中80~100之间出现明显的峰值变化,即是故障信号。同时峰值越突出的地方即是故障越严重的位置。
2 故障诊断试验平台
本实验所使用的齿轮箱实验装置由动力系统、传动系统和磁粉加载器三部分组成。试验台的结构示图如图8a所示,实物装置如图8b所示。

图8 实验台结构图
本实验台采用三相异步电动机作为动力源,采用变频器进行调速。图8b中1为三相异步电动机(1),2为变频器,3为一级齿轮箱,4为电磁粉末制动器,5为三相异步电动机(2),6为二级齿轮箱,7为电磁粉末制动器。电动机(1)的型号为Y80M2-4,其功率为0.75kW,转速为1390r/min,频率50Hz;电动机(2)的型号YYJ110-440-4,其功率为400W,转速为1350r/min,频率为50Hz。变频器的调速范围为0~150Hz,输出功率为1.5kW。
一级齿轮箱的型号为ZDY100,其传动比为1:81.5;二级齿轮箱的型号为ZLY112,其传动比为1:10。
电磁粉末制动器的型号为GXFZ-B-6,额定转矩为6N·m,通过激磁电流进行加载,达到模拟齿轮箱工作负载的作用。
齿轮箱振动信号的测试系统由传感器,数据采集卡和动态信号分析软件等组成。
本实验系统选用的传感器是YD-37型压电式加速度传感器[8]。为了安装和拆卸方便,以及检测的准确性,选择了通过打孔将其与减速器直接安装,从而大大方便了采集的灵活性和装卸的方便及不易损坏。
本实验选用ADLINKPCI-9111系列采集卡[9],其为16通道,多功能、低价位数据采集卡,具有模拟输入、配置容易的特点。
3 仿真结果与分析
本文所采用的旋转机械为一级齿轮箱和二级齿轮箱[10]。主要检测其齿轮振动故障和轴承振动故障,其测点如图9所示。

图9 齿轮箱检测点分布图
通过对一级减速器、二级减速器的数据采集得到两组数据:5746、4731。分别对采集的两组数据进行分析,得到两组时域波形图与残差图,如图10所示。

图10 两组时域波形图与残差图
数据5746的波形图中有较多突出峰值,从其时域波形图中很难看出信号中是否有故障信息,无法对齿轮箱进行故障诊断。而经过处理后的残差图中可以看见明显的突出峰值,即是故障信号位置。峰值所在区域对应的位置即是齿轮发生故障的位置。而数据4731的时域波形图经处理后无明显变化。所以齿轮箱无明显故障。
4 结束语
观察时域平均后的齿轮振动波形对于识别故障类型帮助很大,即使一时难以得出明确的结论,对后续分析和判断也可以提供极具参考价值的信息。本文基于残差信号分析技术对齿轮及齿轮箱进行状态监测与故障诊断,实现齿轮箱由事后维修、定期维修到视情维修的根本转变,减少一些不必要的经济损失,从而在风力发电机组中创造更大的经济效益和社会效益。
[1] 游子跃,王宁,李明明,等.基于EEMD和BP神经网络的风机齿轮箱故障诊断方法[J].东北电力大学学报,2015,35(1):64-72.
[2] 徐英帅,王细洋,孙伟.基于小波变换的齿轮箱故障诊断[J].组合机床与自动化加工技术,2012 (2):66-71.
[3] 曹玉苹,田学民. 基于典型变量分析状态残差的故障检测方法[C].全国技术过程故障诊断与安全性学术会议,2007:74-76.
[4] 肖白,杨修宇,穆钢,等.基于多变量分析的城市电网空间负荷预测方法[J].东北电力大学学报,2013,33(1/2):39-44.
[5] 胡贵锋,王细洋. 基于时域同步平均法的行星齿轮振动信号分离技术[J].中国机械工程,2013,24(6):787-791.
[6]CooleyJamesW,TukeyJohnW.AnalgorithmforthemachinecalculationofcomplexFourierseries[J].Math.Comput,1965,19: 297-301.
[7] 张贤达.现代信号处理[M].2版.北京:清华大学出版社,2002.
[8] 陆兆峰,秦旻,陈禾,等. 压电式加速度传感器在振动测量系统的应用研究[J].仪表技术与传感器, 2007(7):3-4.
[9] 余文成. 基于数据采集卡PCI-1711L的振动测试系统的设计[J].计量与测试技术, 2009, 36(11):62-63.
[10] 夏松波,张礼勇. 旋转机械故障诊断技术的现状与展望[J]. 振动与冲击, 1997(2):1-5.
(编辑 李秀敏)
Fault Diagnosis Analysis And Simulation for Gear Based on Vibration Signal Residual Method
TIAN Yuan-yuan,LI Chao-yi
(Institute of Mechanical Engineering,Northeast Dianli Universty,Jilin Jilin 132012,China)
At first, in the paper vibration signals have been collected and dealt based on time synchronous averaging (TSA) in order to prevent gear fault. Then fast Fourier transform method has been used in order to make signals averaged into two parts, so normal signal and fault signal of gear has been obtained. After calculating valid residual value, quantitative presentation of fault variety can be gotten. By comparing, the results show that there is no difference in time domain waveform, while vibration amplitude is smaller in residual error diagram than in time domain waveform. The fault signal is in the place of obvious peak value where the prominent position of peak value is the place of the most serious fault.
gear fault diagnosis; vibration signal; residual error method; time synchronous averaging (TSA); MATLAB
1001-2265(2017)01-0095-03
10.13462/j.cnki.mmtamt.2017.01.026
2015-12-12;
2016-03-11
吉林省教育厅科研项目(2010290);企业横向项目(2012220202000228);东北电力大学研究项目(201201)
田原嫄(1979—),女,长春人,东北电力大学副教授,博士,研究方向为三维测量技术、机械设备故障诊断、优化设计,(E-mail)328965859@qq.com。
TH132;TG506
A

