基于改进S变换的高频地波雷达阵列信号DOA估计*
田潇潇,刘爱军,李春鹏
(哈尔滨工业大学(威海)信息与电气工程学院,山东 威海 264209)
基于改进S变换的高频地波雷达阵列信号DOA估计*
田潇潇,刘爱军,李春鹏
(哈尔滨工业大学(威海)信息与电气工程学院,山东 威海 264209)
传统阵列信号的DOA估计可以同时对空间不同方向上的多个信号源实现方向估计,为了提高估计精度,可以进行时频变换,但小波及希尔伯特黄变换等,都存在交叉项问题,而S变换可以避免交叉项的影响。由于S变换中高斯窗宽度为频率的倒数,为提高信号的时频分辨率,本文在高斯窗中加入调节因子,可以灵活调节高斯窗函数随频率尺度的变化趋势。本文将改进S变换与阵列信号DOA估计结合,通过计算机仿真给出了该方法与传统方法的性能对比,并与高频地波雷达的实测数据结合,验证了此方法的有效性与可行性。
改进S变换; 阵列信号; DOA估计; 时频变换
工作在短波波段(3~30 MHz)的高频地波雷达(High Frequency Surface Wave Radar,HFSWR)利用垂直极化电磁波能够沿海面绕射的原理[1],在海上及低空飞行目标超视距探测、大面积海洋环境监测等军事领域取得了巨大成功[3]。高频地波雷达超分辨测向本质上是阵列空域信号处理,属于空间谱估计的范畴[2]。
在过去30多年中,使用空间内按某种规则排列着的传感器所形成的阵列来接收信号[4],通过分析空域、频域、时频或时频域提取人们所感兴趣的有用信息,从而进行被测信号的参数估计是当今信号处理研究的一个非常重要分支[5]。其本质是使用空间内按一定规律排列着的传感器阵列,通过多通道来获取信号源的空域和时域等等多维的信息,从而达到接收信号和提取所接收到的信号参数的目的[7]。阵列信号处理已经被广泛的应用到声呐、地质勘探、雷达、通信、生物医学等等实际应用工程中,并且取得了很好的实际效果[8]。早在 1940 年,传感器阵列就已经被应用到了雷达领域。时频分析的方法可以分为线性时频分析、双线性时频分析、参数化时频分析等。典型线性时频分析有短时傅立叶变换、Gabor 变换[9]、小波变换以及最近提出的 S 变换的方法等等,而典型的双线性时频分析方法有 Wigner-ville 分布等等[11];近年以来,参数化的时频分析的方法也逐渐的发展起来了。
S 变换是近 10 年来发展起来的一种新型的时频变换[12],最初是由 stockwell(1996)等人提出。其是以 Morlet 小波为基本小波的连续小波变换延伸。现在,对 S 变换的研究主要是对一维时间序列进行研究,并且已经运用到了一些实际的工程运用中[14],如电力信号中用于监测电能质量异常、地震信号用于检测油气异常和医学领域中用于多普勒分析等等。
本文针对阵列信号波达方向处理中分辨率较低的问题,创新性的提出将改进S变换与阵列信号DOA估计相结合的思想,并使用蒙特卡洛法仿真分析了不同信噪比、不同MUSIC算法下,使用改进S变换及普通DOA估计的结果的不同之处,验证了该方法在实际应用中的效果。
1 理论部分
1.1 DOA估计基本的阵列信号模型
本文中波达方向估计系统都可以看成3个组成部分:来波信号、均匀线阵接收信号以及用阵列信号处理知识得到DOA估计值。相对应也可以把DOA估计系统分为目标空间、信号采集空间和信号处理空间(见图1)。
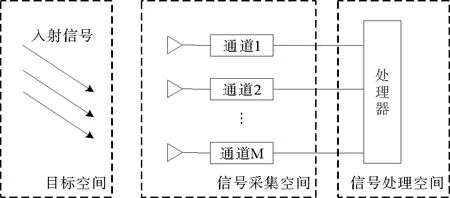
图1 DOA估计系统端口网络示意图Fig.1 Schematic diagram of DOA estimation system port network
从图1中可以看出,对信号波达方向估计的过程就是通过信号采集空间中得到的信息对目标空间中的入射信号的DOA值进行估计的过程。信号DOA估计值的精确程度取决于很多因素,比如所用算法的优劣程度、系统外部的环境、通道以及频带不一致、阵列误差等。
本文所用阵列都是均匀直线阵(Uniform Linear Array,ULA),各天线阵元以一定间距均匀排列在一条直线上。我们假设接收天线阵有M个阵元,阵元间距为d,一个信号源以平面波的形式入射到均匀直线阵上,我们要估计信号的波达方向指的是信号的入射方向与阵列法线之间的夹角θ(见图2)。
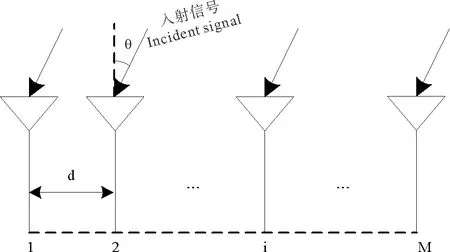
图2 均匀直线阵列示意图Fig.2 Schematic diagram of uniform linear array
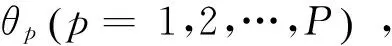
(1)
那么第m个阵元接收到的第p个信号的时延可以写为:
(2)
这里c指的是光速。则第m个阵元上的接收信号可以表示为:
(3)
式中:m=1,2,…,M,gmp表示第m个阵元对第p个信号的增益;τmp表示第p个信号到达第m个阵元时和参考阵元相比所产生的时间延迟;nm(t)表示第m个阵元在t时刻的噪声。
将式写成矢量形式如下:
X(t)=AS(t)+N(t),
(4)
式中的X(t)表示阵列的M×1维的矢量;A表示阵列的M×P维的阵列流型矩阵,也称导向矢量矩阵;S(t)表示的是N×1维的接收信号矢量;N(t)表示的是M×1维的噪声矢量。
1.2MUSIC算法的原理
由1.1节的阵列信号模型可知,窄带远场信号的接收模型如公式所示,那么接收阵列的协方差矩阵可以写为:
RX=ARSAH+RN=ARSAH+σ2I,
(5)
式中:RS表示的是有用信号的协方差矩阵;RN表示的是接收噪声的协方差矩阵;σ2表示的是高斯白噪声的方差;I表示单位阵。

假设λi是矩阵RX的第i个特征值,νi是和λi相对应的特征向量,那么有:
Rxνi=λiνi,
(6)
再假设λi=σ2是协方差矩阵RX的较小的特征值,则有:
Rxνi=σ2νi,i=P+1,P+2,…,M,
(7)
将式代入上式,可以得到:
(8)
对上式进行化简,可得:
ARsAHνi=0,
(9)
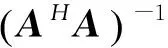
AHνi=0,i=P+1,P+2,…,M,
(10)
式(10)可以表明:代表噪声的特征值所对应的特征向量νi与导向矢量矩阵A的列向量之间是正交的,而导向矢量矩阵的每一列和来波信号相对应,因此利用噪声和信号之间的正交性再通过谱峰搜索就可以得到信号的来波方向。
把噪声的特征向量放在一起构造出一个噪声子空间矩阵En:
(11)
定义空间谱Pm(θ):
(12)
式(12)是我们构造的空间谱的表达式,式中分母代表的是导向矢量矩阵和空间噪声矩阵的内积,也就是说当a(θ)和噪声子空间的每一列都正交时,空间谱表达式的分母就为零。又由于噪声的存在,空间谱表达式的值会表现为一个最小值,此时Pm(θ)呈现的是一个尖峰。因此我们让θ逐渐变化,通过寻找空间谱的谱峰就可以得到信号来波方向的值,这就是经典MUSIC算法的原理。
1.3S变换及改进S变换的相关知识
1996年,R.G.Stockwell等人提出S变换。S变换是连续小波变换思想的一种推广,它具有连续小波变换所欠缺的某些性质,它基于一个平移伸缩局部化的高斯窗,用它对非平稳信号进行检测时,不仅能保持与频率有关的分辨率,而且与傅里叶频谱也有直接的联系,这是其它任何变换所没有的性质。其变换公式为:
(13)
由于S变换的基本小波是固定不变的,因此,在解决实际问题时也受到了某种程度的限制。随后,很多学者在此基础上对S变换中的基本小波或窗函数进行了改进,得到了改进S变换,例如,高静怀等在S变的基础上,对其基本小波做了进一步的推广,采用四个参数(振幅、能量衰减率、能量延迟时间及视频率)来控制基本小波,故可以根据实际问题的特点选择最佳的小波。
下面来介绍改进S变换的具体公式。
设h(t)∈L2(R),在S变换中,基本小波函数为:
(14)
h(t)相对于w(t)的改进S变换定义为:
(15)
(16)
其中:gf(t)为高斯窗函数;A是基本小波幅度;α是能量衰减率;β是能量延迟时间;f0是基本小波视频率。
通过归纳可发现,改进S变换的窗函数可表示为两部分相乘的模式
gf(t)=γ1γ2。
(17)
通过改变γS中的γS,可改变窗函数的形态,γS取值越大,改进S变换的窗函数越宽,反之越窄,这样就可以在实际的高频地波雷达信号处理时,根据不同的时间分辨率和频率分辨率的要求,选择不同的γS值。为了得到较好的时间分辨率,可以选择较窄的窗函数,γS选取趋近于0,但这时频率窗函数就会较宽,所以不能获得较高的频率分辨率。因此在γS的选取上就应该根据具体需要综合考虑。
1.4 基于改进S变换的阵列信号DOA估计
由于改进S变换是线性时频分析函数,所以要构造基于改进S变换的时频协方差矩阵,这样就可以满足使用MUSIC算法的矩阵结构。
第m个阵元在t时刻接收的信号为:
(18)
其中:sn(t) 为第n个信号源在t时刻的信号波形;τm为相对于第一个阵元接收信号的时延;zm(t) 为第m个阵元接收的噪声。
对(20)式作改进S变换得:
(19)
其中
(20)
x(f,t)=[x1(f,t),x2(f,t),…,xM(f,t)]T,
(21)
(21)式也可以表示为:
x(f,t)=A(f)s(f,t)+z(f,t),
(22)
其中
s(f,t)=[s1(f,t),s2(f,t),…,sN(f,t)];
(23)
经过改进S变换的协方差矩阵为
Rx(f,t)=E[x(f,t)xH(f,t)]=
A(f)Rs(f,t)AH(f)+Rz(f,t)。
(24)
从其矩阵结构可得可以使用MUSIC算法进行DOA估计。
2 仿真分析
使用蒙特卡洛法,分别在不同信噪比、不同阵元数的情况下,仿真对比MUSIC算法、权矩阵为w=e×eT,e=[1 0 0 …0]T的加权MUSIC算法及求根MUSIC算法的均方误差,确定哪种方法更适合与改进S变换结合;之后进行S变换、改进S变换的阵列信号DOA估计,并进行对比分析。
图3的仿真实验对比了在信噪比一定的情况下,阵元数不同时,三种MUSIC算法的均方误差,令信噪比为0dB,信源数为1;信号长度为1 024;快拍数为1 024;信号频率为0.785MHz;阵元间距为λ/2;信号入射角度为50°。
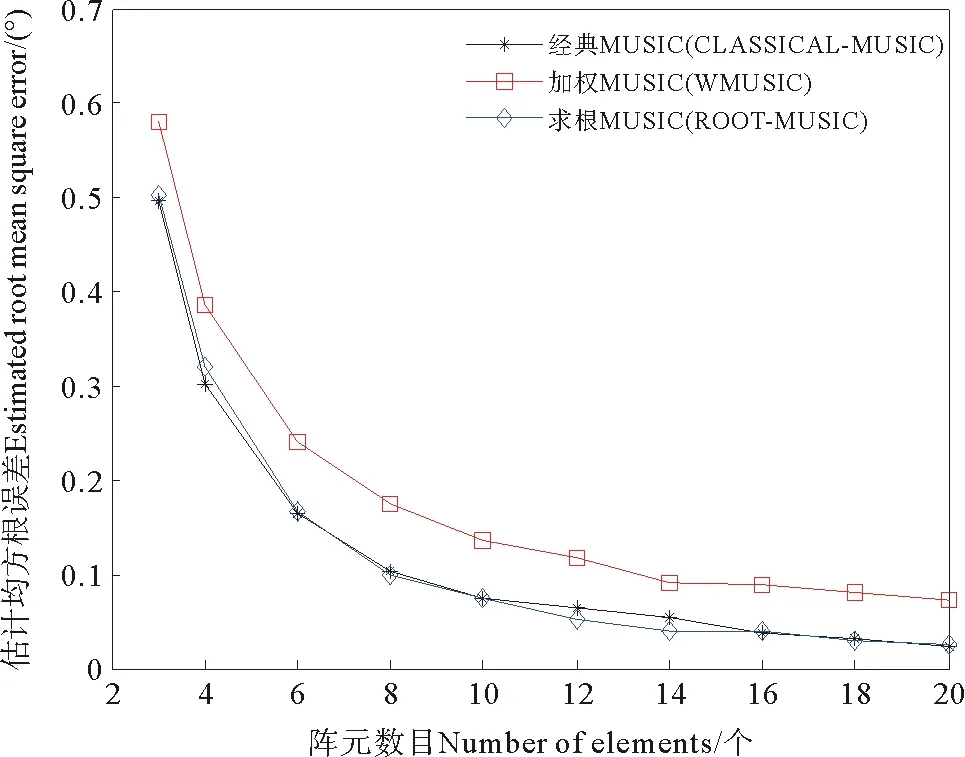
图3 不同阵元数下的对比
图4的仿真实验对比了在阵元数一定的情况下,信噪比不同时,三种MUSIC算法的均方误差,令阵元数为8;信源数为1;信号长度为1 024;快拍数为1 024;信号频率为0.785MHz;阵元间距为λ/2;信号入射角度为50°。
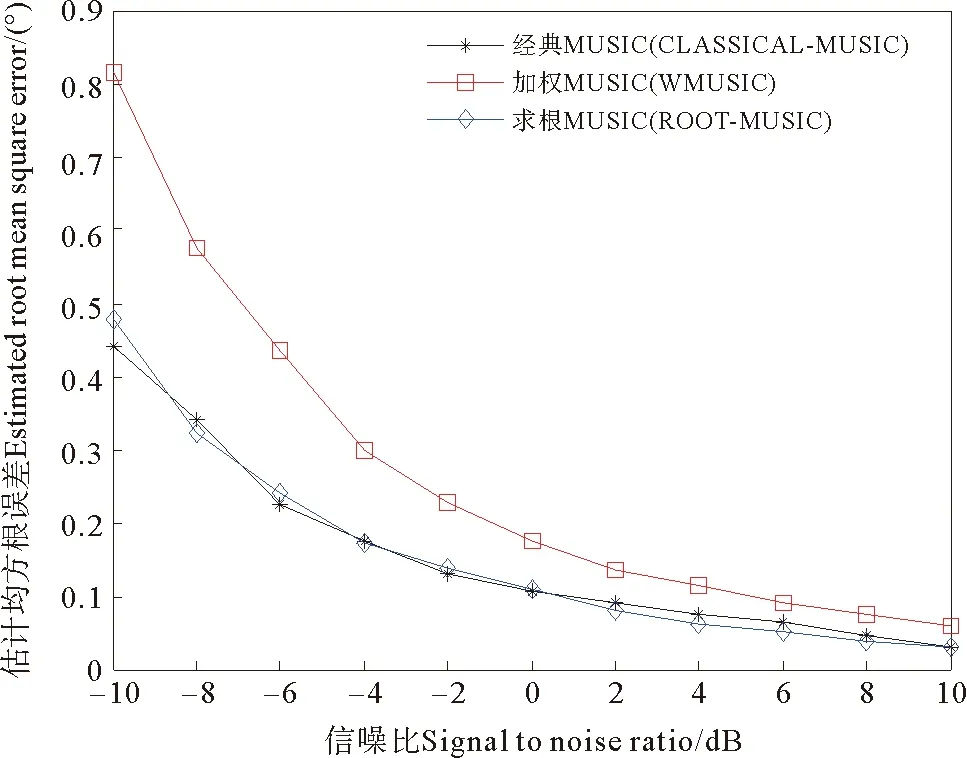
图4 不同信噪比下的对比Fig.4 Comparison of different signal to noise ratio
从上面两图可以分析出,此处权函数为w=e×eT的加权MUSIC算法对线性调频信号的分辨率较差,所以,本文接下来选择经典MUSIC算法进行DOA估计。
图5是线性调频信号进行改进S变换之后的时频图,采样点数为250个,信噪比为10dB,归一化频率分别为(0.1,0.2),(0.3,0.4)。可见改进S变换可以避免小波变换等变换出现交叉项的问题,但时频聚集性较差。
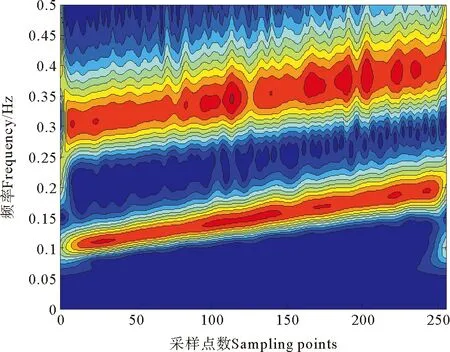
图5 改进S变换后的线性调频信号
想要将上述信号进行分离,由1.4节可知,经过改进S变换后的信号,由于是线性变换,所以只要构造符合MUSIC算法的矩阵结构的协方差矩阵,就可以利用MUSIC算法进行角度估计。
图6、7分别是阵元数为8;信源数为2;信号长度为1 024;快拍数为1 024;信噪比为0dB;信号频率为0.785MHz;阵元间距为λ/2的信号,进行了S变换及改进S变换后,在入射信号为30°和35°时的DOA估计对比。可见运用改进S变换比S变换的DOA估计精度要更加精确。
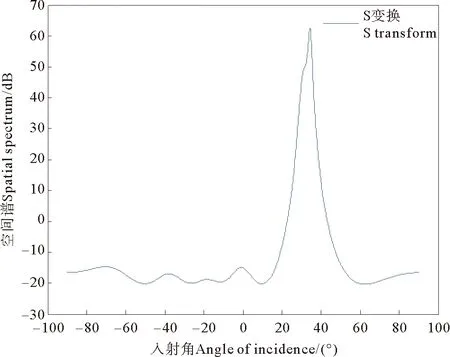
图6 S变换后的DOA估计
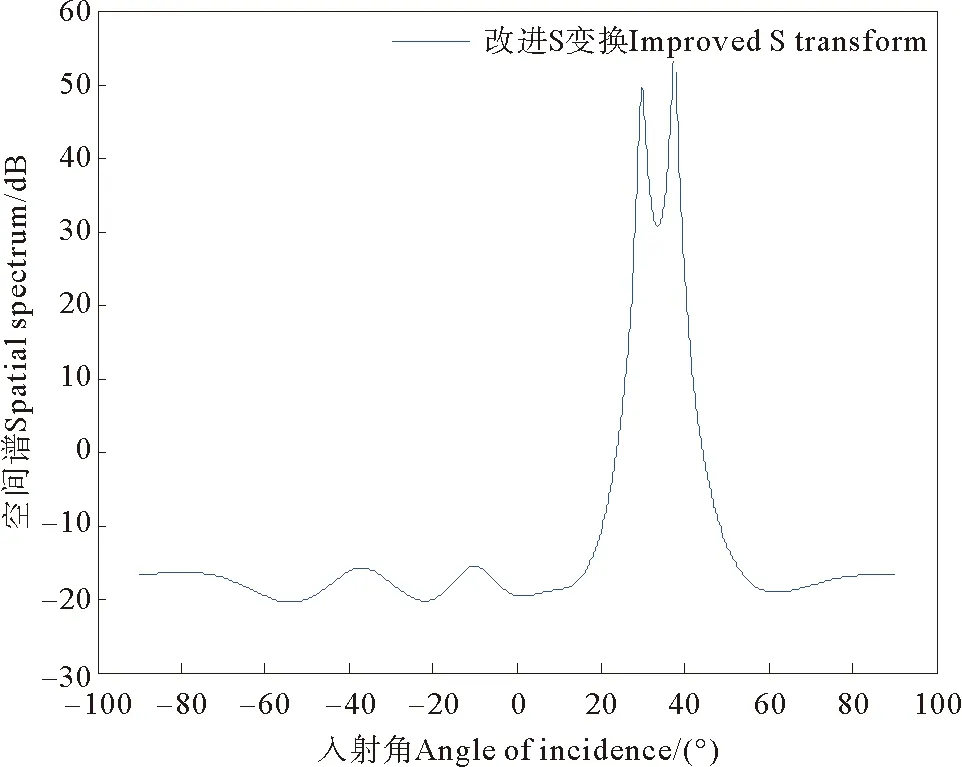
图7 改进S变换后的DOA估计Fig.7 DOA estimation based on improved S transform
高频地波雷达的天线阵是由多阵元组成的,从θ方向来的信号在不同阵元输出的信号较基准阵元(阵元一)有一行程差,从而产生一相位差Δφl
(25)
其中:l=0,1,2,3,4…代表不同阵元;d为阵元间距;为雷达波长;θ为雷达回波入射角。
则第l路阵元的接收信号相位为
PRI(t)=2πf0(t-tr)+2πfb(t-nTr-tr)+πk(t-nTr-tr)2+φ0-ΔφI,
(26)
式(26)中相位差ΔφI,其对应1.1节中的相位差Δmp,将其代入MUSIC算法的公式中,可以此提取目标方位信息。
高频地波雷达一般工作在 3~30MHz,其波长较长,与常规的微波雷达相比,其方位分辨率较差,所以要寻找提高方位分辨率的方法,本文尝试将改进S变换的DOA估计与高频地波雷达的实测数据相结合。
所用数据为接收阵列为8元均匀线阵,载波频率为3.7MHz,采样点数为1 024,距离门数为194,每个距离门宽度为1.5km,为了验证算法是否准确,向实测数据中添加两个参考信号,方位角已知。向实测数据的第73~75个距离门中加入2个线性调频目标,其归一化频率分别为0.01~0.012以及0.018和0.02,方位角分别为0°和2°,信噪比约为15dB,所设目标与真实情况接近,分别用经典MUSIC算法、基于S变换的MUSIC算法和基于改进S变换的MUSIC算法对参考信号进行DOA估计。
从表1中可以看出,把改进S变换应用到高频地波雷达阵列测向中是一种可行的思想,表中得到DOA估计值对应的实际方位角分别为0°和2°,用改进S变换的DOA估计算法估计的结果是较准确的,有较大的参考价值。
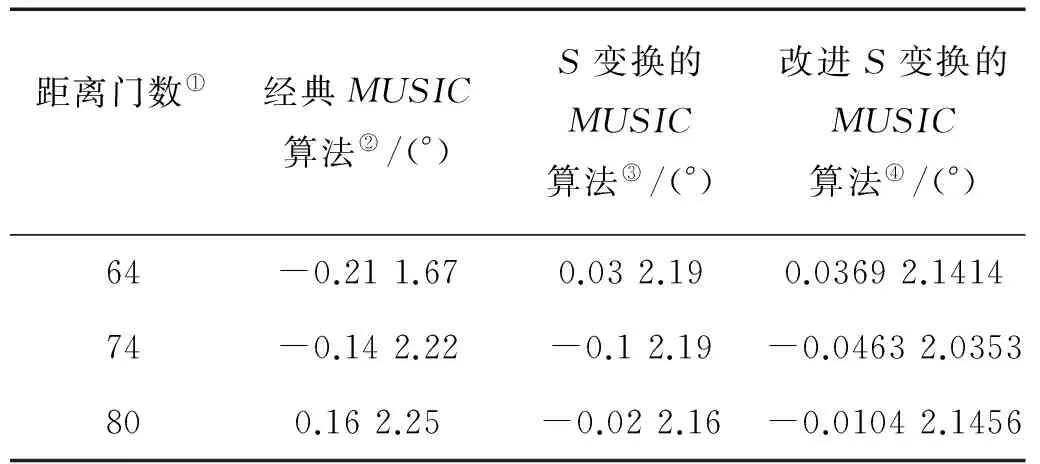
表1 三种算法的DOA估计值
Note:①Distancegate;②ClassicalMUSICalgorithm;③MUSICalgorithmbasedonStransform;④MUSICalgorithmbasedonimprovedStransform
3 结语
本文提出了一种基于改进S变换的阵列信号DOA估计。首先分析了理论基础,之后进行了仿真分析,分别对3种MUSIC算法、线性调频信号进行改进S变换之后的时频图、基于S变换的DOA估计及基于改进S变换的DOA估计进行仿真,可得经典MUSIC算法在分析线性调频信号时的效果最好。改进S变换对线性调频信号进行时频变换后的聚集性较差,改进S变换比S变换在阵列信号的DOA估计时的分辨率要更精确。最后还用高频地波雷达的实测数据对该方法进行了验证,通过3种估计方式的对比,发现用改进S变换的DOA估计算法估计的结果是较准确的,有较大的参考价值。
[1]JohnsonDH,DudgeonDE.ArraySignalProcessing:ConceptsandTechniques[M].Prentice-Hall:Simon&Schuster,2012.
[2]ChenVC,LingHao,Jointtime-frequencyanalysisforradarsignalandimageprocessing[J].IEEESignalProcessingMagazine,2013,16(2):81-93.
[3]GodaraLC,Applicationsofantennaarraystomobilecommunications.I.Performanceimprovement,feasibility,andsystemconsiderations[J].Proc.ofIEEE,2011,85(7):1031-1060.
[4]SayedAH,TarighatA,KhajehnouriN,Network-basedwirelesslocation:challengesfacedindevelopingtechniquesforaccuratewirelesslocationinformation[J].SignalProcessingMagazine,IEEE,2015,22(4):24-40.
[5]WuWW,MillerEF,PritchardWL,etal.Mobilesatellitecommunications[J].ProcofIEEE,2014,82(9):1431-1448.
[6] 李大心.探地雷达方法与应用[M].北京:地质出版社,2014.
[7]SkolnikMI,RadarHandbook[M].NewYork:McGraw-Hill,2011.
[8]DavisPJ.InterpolationandApproximation[M].NewYork:Dover,2012.
[9]WinM,ScholtzR.Ultra-widebandwidthtime-hoppingspread-spectrumimpulseradioforwirelessmultiple-accesscommunications[J].IEEETransonCommunications,2011,48(4):679-691.
[10]FriedlanderB,WeissAJ.Directionfindinginthepresenceofmutualcoupling[J].IEEETrans.onAntennasandPropag.,2011,39(3):273-284.
[11]BarbarossaS,ScaglioneA,GiannakisGB.Producthigh-orderambiguityfunctionformulticomponentpolynomial-phasesignalmodeling[J].IEEETransonSignalProcessing,2011,46(3):691-708.
[12]PelegS,PoratB.TheCramer-Raolowerboundforsignalswithconstantamplitudeandpolynomialphase[J].IEEETransSignalProcess,2011,39(3):749-752.
[13] 华夏.小型化高频雷达接收阵列的研究[D].哈尔滨:哈尔滨工业大学,2011.HUAXia.ResearchonSmallSizedHighFrequencyRadarReceivingArray[D].Harbin:HarbinInstituteofTechnology,2011.
[14] 陈学华,贺振华.改进的S变换及在地震信号处理中的应用[J].数据采集与处理,2005,20(4):449-453.ChenXuehua,HeZhenhua.ImprovedStransformanditsapplicationinseismicsignalprocessingApplication[J].Dataacquisitionandprocessing,2005,20(4):449-453.
[15]XiongbinW,FengC,ZijieY,etal.BroadbeamHFSWRarraycalibrationusingseaechoes[C].Shanghai:2006CIEInternationalConferenceonRadar,2006.
[16] 刘传武,张智军,毕笃彦.S变换在雷达目标识别中的应用[J].系统仿真学报,2008,20(12):3290-3292.LiuChuanwu,ZhangZhijun,Stransforminradartargetrecognition.Journalofsystemsimulation[J].2008,20(12):3290-3292.
责任编辑 陈呈超
Array Signal DOA Estimation Algorithm Based on Improved S-Transform
TIAN Xiao-Xiao1,LIU Ai-Jun2,LI Chun-Peng3
(School of Information and Electronic Engineering,Harbin Institute of Technology (Weihai),Weihai 264209,China)
The DOA estimation of traditional array signals can simultaneously estimate the direction of multiple sources in different directions in the space,but in the actual environment,the array errors are almost inevitable.In order to improve the estimation accuracy,the time-frequency transform can be performed,but the wavelet and Hilbert Huang transform have the cross term problem,while the S transform can avoid the influence of the cross term.Because the Gauss window width is the reciprocal of the frequency in the S transform,in order to improve the time-frequency resolution of the signal,the adjustment factor is added into the Gauss window,which can flexibly adjust the change trend of the window function with the frequency scale of the.Improved discrete transform algorithm) is smaller than the traditional operation algorithm,is due to the influence of window function,the improved algorithm will remove redundant operations outside the window function; and the modified discrete transform) algorithm is smaller than the continuous wavelet transform algorithm,a very important reason is because the discrete transform algorithm) use butterfly algorithm fast Fourier transform.The improved S transform and DOA estimation of array signal combining,by comparing the performance of computer simulation is given with the traditional methods,and the measured data and the HF radar combination,verify the feasibility and validity of this method.
improved S-transform; array signal; DOA estimation; time frequency transform
国家海洋公益项目(201505002);国家自然科学基金面上项目(61571157);哈工大(威海)学科引导基金项目(WH20150111)资助
Supported by the National Marine Public Welfare Project (201505002); National Natural Science Foundation of China (61571157);Harbin Institute of Technology (Weihai) Science Guide Fund (WH20150111)
2016-09-15;
2016-10-04
田潇潇(1992-),女,硕士。E-mail:504679488@qq.com
TN953+.5
A
1672-5174(2017)02-050-06
10.16441/j.cnki.hdxb.20160229
田潇潇,刘爱军,李春鹏.基于改进S变换的高频地波雷达阵列信号DOA估计[J].中国海洋大学学报(自然科学版),2017,47(2):50-55.
TIAN Xiao-Xiao,LIU Ai-Jun,LI Chun-Peng.Array signal DOA estimation algorithm based on improved S-transform[J].Periodical of Ocean University of China,2017,47(2):50-55.

