一种无类型的弱公理化真理论及其扩充
李 晟
(四川师范大学 逻辑与信息研究所,成都 610068)
一种无类型的弱公理化真理论及其扩充
李 晟
(四川师范大学 逻辑与信息研究所,成都 610068)
在概述弱公理化真理论与无类型的弱公理化真理论PUDT的基础上,证明无类型去引号理论,即正一致去引号理论(positive uniform disquotational theory,简记为PUDT)是一种正真(positive truth)的弱公理化真理论。对PUDT进行适当扩充,可以得到在经典逻辑上不相容,而在直觉主义逻辑上相容的公理化真理论。但是,这类公理化真理论并不是理想的真理论。
公理化;真理论;弱组合性;无类型
一、什么是弱公理化真理论
弱公理化真理论是指对真概念的组合性原则进行弱化处理。组合性认为复杂表达式的语义值是由其句法组成模式和组成成分的语义值所决定的。组合性对真概念的日常语言实践十分重要。莱特戈布(H.Leitgeb)将真概念的组合性作为理想真理论应当具备的8个标准之一[1]280-281。
在通常情况下,组合性原则是以一阶全称量化语句来表达的,并且一般是将这些语句直接作为公理化真理论的真之公理。经典的公理化真理论的塔尔斯基组合理论CT、Friedman-Sheard理论FS以及Kripke-Feferman理论KF都是这样的真理论。去引号理论DT比较特别,它是以受限制的塔尔斯基双条件句的所有实例为真之公理,在形式上并不能体现组合性,但是相比前面3种真理论,其真之公理简单而直观。然而,DT的主要缺点是弱演绎力,即DT不能证明包含真谓词的全称量化语句。这就意味着DT没有组合性。但霍斯顿(L.Horsten)认为,若是以公理模式重新表达CT的组合公理,就应当可以证明这些组合公理能够由DT推出[2]71。
以公理模式而非一阶全称量化语句表达组合性原则,称为弱组合性。满足弱组合性的公理化真理论称为弱公理化真理论。埃德尔(G.Eder)在论文《组合性与弱公理化真理论评论》[3]中,首次提出并讨论了弱公理化真理论。在这篇论文里,埃德尔反驳了霍斯顿关于DT与CT相互关系的观点。埃德尔证明,DT不能推出CT的全称量词组合公理的模式版本[3]545。这就说明霍斯顿的设想其实并不成立,从而也表明在DT与CT之间确实还存在着弱公理化真理论。直接弱化CT的组合公理所得到的真理论,虽然可以具备弱组合性,但是并没有实际价值。埃德尔希望,弱公理化真理论不仅要能够满足弱组合性,还要能够在形式上具备DT的简单直观性。埃德尔证明,一致去引号理论(uniform disquotational theory,简记为UDT)是介于DT和CT之间的弱公理化真理论[3]546-547。
但是,UDT是一种类型的(typed)公理化真理论。类型真理论虽然可以避免说谎者悖论,但是由于它们不允许真谓词自由迭代,以至于很多直观上成立的语句却不能被类型真理论接受。比如,“0等于0是真的”是真的。因此,类型真理论具有比较明显的局限性。本文将在埃德尔工作的基础上,尝试找出一种无类型的(type-free)弱公理化真理论。

二、无类型的弱公理化真理论PUDT
对于无类型的弱公理化真理论,我们仍然坚持两条标准:弱组合性与真之公理的简单直观。先看真之公理的简单直观。在已有的无类型公理化真理论中,满足这一要求的只有无类型去引号理论PUDT,所以接下来只需考察PUDT是否还能满足弱组合性。再看弱组合性。无类型的弱组合性有两种可能的方案;一是将FS的真之公理进行弱化处理,二是将KF的真之公理进行弱化处理。
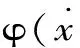
定义2(正真公式) LT公式φ被称为正真公式,当且仅当φ中不包含前缀奇数个否定词的T谓词。当φ是闭公式时,称为正真语句。

从真之公理的直观简单性上看,PUDT与类型弱公理化真理论UDT极为相似。UDT能够证明CT真之公理的弱化版本,那么作为CT的无类型扩充理论的FS,PUDT也就期待能够证明FS真之公理的弱化版本。但是,由于PUDT只能处理正真公式,所以其弱组合性也只能限制为关于正真公式的弱组合性。现在考虑FS意义上的弱组合性。弱化FS的真之公理将得到:
WFS1:T┌φ┐↔ Val+(┌φ┐),φ是LPA原子语句;


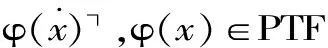

定义3(PWKF) 无类型正真弱组合理论PWKF是以正真公理模式的形式重新表达KF的真之公理所得。包含以下13条真之公理:
PWKF1:T┌φ┐↔Val+(┌φ┐),φ是LPA原子语句;






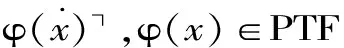

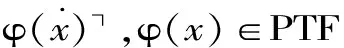

PWKF12:T┌T┌φ┐┐↔T┌φ┐,φ是LT语句;


定义4(无类型正真弱组合性) 如果一种真理论能够证明PWKF的组合公理PWKF1至PWKF12,那么就称这种真理论满足无类型正真弱组合性。
定理1PUDT满足无类型正真弱组合性。
证明:只需证明PWKF1至PWKF12均能为PUDT证明。首先验证含T谓词的原子语句的情形,PWKF12即为PUDT真之公理的代入特例。
其次,验证等式原子语句和逻辑联结词、量词的情形。


其余情形可以类似地验证。
关于PUDT的其他性质,哈尔巴赫(V.Halbach)证明,PUDT能够定义KF的T谓词[4]280-282,但他同时证明了PUDT的T谓词不满足KF的组合性,因为PUDT的弱演绎力使得它无法证明涉及T谓词的全称概括语句[5]794。但定理1表明,PUDT能够在埃德尔弱组合原则的意义上证明KF的正真弱组合公理。所以,PUDT的确是一种关于正真的无类型弱公理化真理论。
三、对PUDT的扩充
考虑由以下两条真之规律组成的真之公理集:
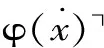

很明显,ST1就是PUDT的真之公理;ST2是FS和KF的析取词真之公理的模式版本。下面定义两种新的公理化真理论:
定义5(CST) 基于经典逻辑的公理化真理论CST是在算术理论PAT的基础上添加ST1和ST2所得。
定义6(IST) 基于直觉主义逻辑的公理化真理论IST是将CST的逻辑基础直接减弱为直觉主义逻辑而得到。
定义7(IPUDT) 把PUDT的逻辑基础直接减弱为直觉主义逻辑,所得理论记为IPUDT。
不难看出,CST是对PUDT的扩充,而IST是对IPUDT的扩充,并且CST与IST的区别仅在于逻辑基础。
定理2CST是相容的。
证明:因为PUDT是KF的子理论[4]276-277,所以ST1是KF可证的;而ST2是对KF公理的直接弱化,因而也能够为KF证明。所以,CST是相容的。
定理3IST是相容的。
证明:根据定义6可知,IST是CST的子理论,所以由定理2可证。
定义8(NEC规则) 对任意LT语句φ,如果能给出φ的证明,那么就能由此得到T┌φ┐。
定义9(CONEC规则) 对任意LT语句φ,如果能给出T┌φ┐的证明,那么就能由此得到φ。
定理4CST对NEC和CONEC封闭是不相容的。

定理5IST对NEC和CONEC封闭是相容的。

一般说来,为了得到一个相容的真概念,需要对真理论做一些限制。通常有3种方式:限制语言、限制逻辑、限制真之规律。限制语言的代表是塔尔斯基的语言层次理论,其成效显著但局限性也十分明显。限制真之规律最为有效,但是在弄清导致不相容性的根源前,急于限制真之规律并不利于真理论的发展。限制逻辑的做法比较少,因为除了经典逻辑和直觉主义逻辑,其他逻辑与日常的推理实践确实相差太远。
在论文《直觉主义逻辑上的Friedman-Sheard方案》[6]中,利(G.E.Leigh)和拉特延(M.Rathjen)认为,真之规律的不相容组合在很大程度上是由于使用了经典逻辑,倘若放弃经典逻辑基础,改为采用直觉主义逻辑,则很可能使原本不相容的组合变成相容。利和拉特延的工作是限制逻辑的一次尝试,但是他们并没有真正给出一个在经典逻辑上不相容而在直觉主义逻辑上相容的组合。
本文以无类型弱公理化真理论PUDT为基础,发现了一组真之规律(即ST1和ST2),当它们以经典逻辑为基础(即CST),并且对NEC规则和CONEC规则封闭,它们是不相容的;而在直觉主义逻辑基础上(即IST)却相容。差别仅在于逻辑基础。这就说明确实存在经典逻辑上不相容而直觉主义逻辑上相容的真之规律的组合,也就表明限制逻辑是可行的。

定义10(IST′) 基于直觉主义逻辑的公理化真理论IST′是在算术理论HAT的基础上添加下列真之公理所得:
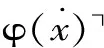



其中,HAT是用LT重新表达海廷算术HA所得。HA与PA的算术公理完全相同,区别只在于逻辑基础,前者是直觉主义逻辑,后者是经典逻辑。

虽然从形式上看,IST′的真公理确实比IST更丰富,但IST′同样不能完整地刻画真谓词的组合性,所以IST′与IST实际上是对PUDT的真之公理的同类型扩充。由此不难想到,如果一组真之公理能够完整地刻画组合性,那么无论这组真之公理是以经典逻辑为基础,还是以直觉主义逻辑为基础,都将得到关于相容性的相同结论,因为经典逻辑可以通过否定性转换嵌入直觉主义逻辑。这也就能说明为什么在利和拉特延的工作中,虽然二人给出了15个基于直觉主义逻辑的极大相容组合,却并没有最终找出一个能在经典逻辑上不相容而在直觉主义逻辑上相容的组合。原因就在于,无论是基于经典逻辑的9个极大相容组合[7]6,还是基于直觉主义逻辑的15个极大相容组合,它们所包含的真之规律都能完整地刻画真概念的组合性。而之所以能在直觉主义逻辑上得到更多的相容组合,是因为减弱逻辑基础后,原本等价的组合现在不等价了,而不是原本不相容的组合现在相容了。
四、结束语
本文主要是对两个问题进行了初步的探讨。一是接续了埃德尔的工作,思考了无类型的弱公理化真理论。我们看到,如果以同时满足真之公理的简单直观性和弱组合性为标准,那么正一致去引号理论PUDT就是现有的一种无类型的弱公理化真理论。但我们同时看到,PUDT只能证明关于正真的弱组合公理,所以它实际上并不等价于KF的直接弱化(WKF)。这就说明,要想找到等价于WKF的公理化真理论,必须对PUDT进行扩充。围绕第二个问题,我们考察了PUDT的扩充理论。我们因此发现了一组特殊的真之规律:如果让它对NEC规则和CONEC规则封闭,那么当它的逻辑基础是经典逻辑时,它是不相容的;而当它的逻辑基础是直觉主义逻辑时,它却是相容的。但是这样的公理化真理论并不能完整地刻画真概念的组合性,所以它们都不是理想的真理论。而这也就说明了由利和拉特延所提出的限制逻辑的方案是有局限性的。
[1] LEITGEB H.What Theories of Truth Should be Like (but Cannot be)[J].Philosophy Compass,2007,2(2):276-290.
[2] HORSTEN L.The Tarskian Turn:Deflationism and Axiomatic Truth[M].Cambridge:MIT Press,2011.
[3] EDER G.Remarks on Compositionality and Weak Axiomatic Theories of Truth[J].Journal of Philosophical Logic,2014(43):541-547.
[4] HALBACH V.Axiomatic Theories of Truth[M].Cambridge:Cambridge University Press,2011.
[5] HALBACH V.Reducing Compositional to Disquotational Truth[J].Review of Symbolic Logic,2009(2):786-798.
[6] LEIGH G E,RATHJEN M.The Friedman-Sheard programme in intuitionistic logic[J].Journal of Symbolic Logic,2012,77(3):777-806.
[7] FRIEDMAN H,SHEARD M.An Axiomatic Approach to Self-referential Truth[J].Annals of Pure and Applied Logic,1987,33:1-21.
(责任编辑张佑法)
A Type-Free Weak Axiomatic Truth Theory and Its Expansion
LI Sheng
(Institute of Logic and Information, Sichuan Normal University, Chengdu 610068, China)
In this paper, we will prove that the type-free disquotational theory, that is, the positive uniform disquotational theory (PUDT), is a weak axiomatic truth theory for positive truth. There exists an axiomatic truth theory, which is consistent on classical logic but not on intuitionistic logic, when PUDT be expanded properly. However, this kind of axiomatic truth theory is not ideal theory of truth.
axiomatic; truth theory; weak compositionality; type-free
2016-07-29
国家社会科学基金项目“公理化真理论研究”(12BZX059)
李晟(1986—),男,四川德阳人,讲师,哲学博士,研究方向:现代逻辑。
李晟.一种无类型的弱公理化真理论及其扩充[J].重庆理工大学学报(社会科学),2017(1):13-17.
format:LI Sheng.A Type-Free Weak Axiomatic Truth Theory and Its Expansion[J].Journal of Chongqing University of Technology(Social Science),2017(1):13-17.
10.3969/j.issn.1674-8425(s).2017.01.003
B81
A
1674-8425(2017)01-0013-05

