中心有孔圆锥形变幅杆声学特性研究

张 宁 宁

(渭南师范学院 数理学院，陕西 渭南 714099)

【现代应用技术研究】

中心有孔圆锥形变幅杆声学特性研究

张 宁 宁

(渭南师范学院 数理学院，陕西 渭南 714099)

根据变截面纵振动的波动方程，对中心有孔圆锥形变幅杆进行系统研究。利用传统方法分析了变幅杆的频率方程及谐振长度、位移节点、放大系数、形状因数、输入力阻抗、等效网络等声学特性，并将有限元模拟结果与理论计算结果进行了对比，结果表明：理论计算结果与有限元模拟所得结果基本一致，误差较小；当变幅杆大小端及长度尺寸不变时，变幅杆理论计算及模拟的频率和放大系数随着中心孔径尺寸的增加而增加。该结论对中心有孔变幅杆的实际工程应用提供理论参考。

声学特性；频率和放大系数；力阻抗；有限元模拟

超声变幅杆是超声波振动系统中一个重要的组成部分，主要作用是把质点的机械振动位移或速度放大。[1-4]超声波变幅杆是配合超声波换能器改变超声波振动幅度的功能组件。压电换能器在超声频电振荡作用下的伸缩变形很小,一般在4～5 μm左右，不能直接传递到被加工工具上，必须借助变幅杆[5-12]。中间有孔的变幅杆放大倍数较大，在超声加工、焊接等应用中被广泛采用，但是其全面的声学特性以及中心孔尺寸对变幅杆性能的影响，对其实际应用至关重要，因此有必要进行系统研究。文献[13]探讨了中间有圆柱孔换能器和变幅杆的设计理论及声学特性，并且成功地应用于超声珩磨装置。文献[14]推导了内孔分别为锥形和柱形的锥形变幅杆的频率方程及各参数表达式，这些文献对中心有孔变幅杆的研究还不够全面和完善。因此，本文根据变截面纵振动的波动方程，利用传统方法分析了变幅杆的频率方程及谐振长度、位移节点、放大系数、形状因数、输入力阻抗、等效网络等声学特性，同时将有限元模拟结果与理论计算结果进行对比，结果表明理论计算结果与有限元模拟所得结果基本一致，误差较小；当变幅杆大小端及长度尺寸不变时，变幅杆理论计算及模拟的频率和放大系数随着中心孔径尺寸的增加而增加，该结论对中心有孔变幅杆的实际工程应用提供了理论参考。

1 中心有孔圆锥形变幅杆的波动方程

根据超声珩磨装置的设计要求，圆锥形变幅杆应有一圆柱通孔，如图1所示，中间有圆柱孔的圆锥形变幅杆纵振动的波动方程为[2]：

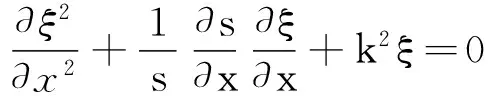
(1)

坐标原点x=0处的直径为R1，x=l处为R2，孔径为R3，其面积函数为 ：

图1 中间有圆柱孔的圆锥形变幅杆示意图

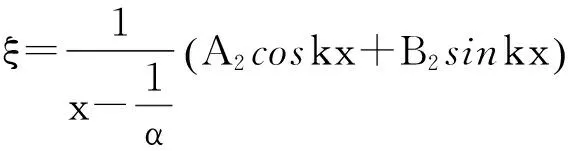
(2)

(3)

2 中心有孔圆锥形变幅杆声学特性

2.1 频率方程及谐振长度

(4)

(5)

2.2 位移节点

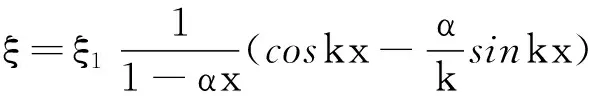
(6)

应力或应变分布表达式为：

(7)

2.3 放大系数

(8)

2.4 输入力阻抗

(9)

将A2、B2代入式(9)，经整理后得：

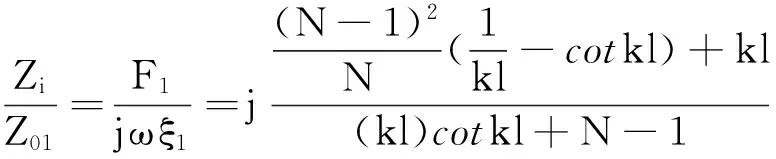
(10)

2.5 形状因数

(11)

(12)

带入式(11)得

(13)

(14)

(15)

式(15)中xM由式(14)及tanθ=α/k可求得。

2.6 等效网络

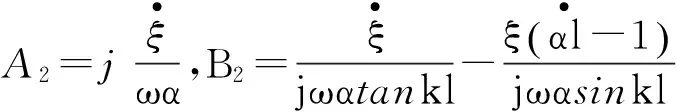
(16)

由式(16)可以确定变幅杆的等效网络如图2所示。

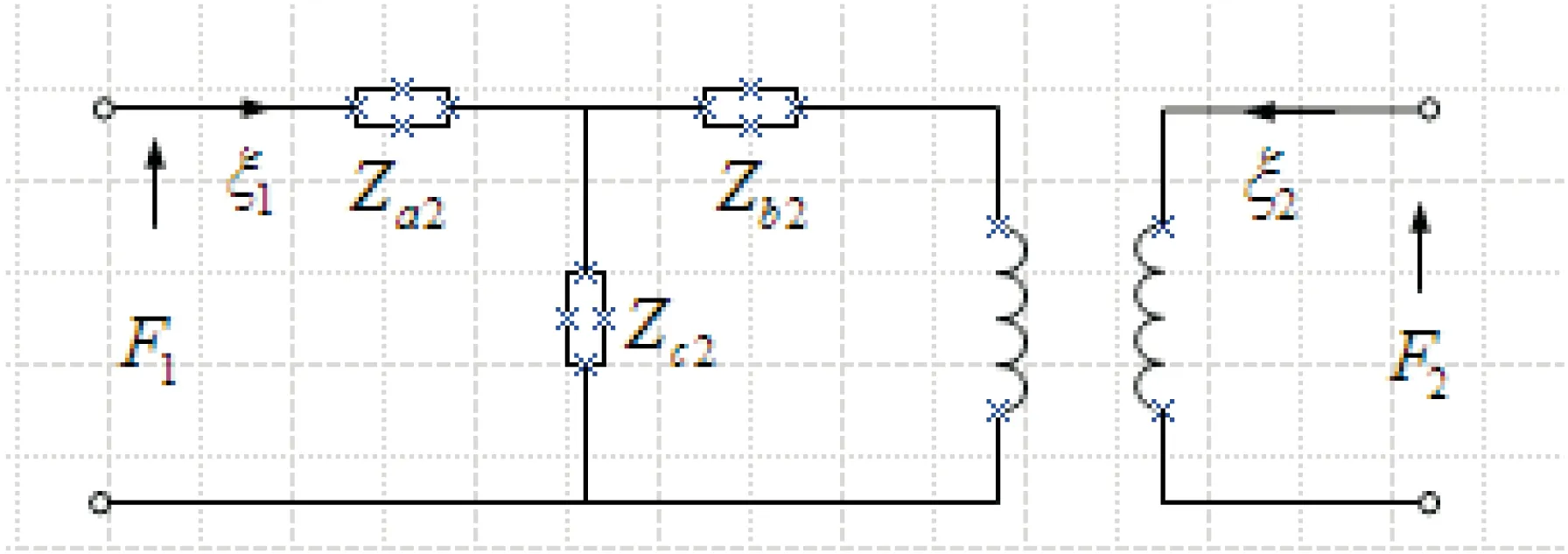
图2 有孔圆锥变幅杆的等效网络

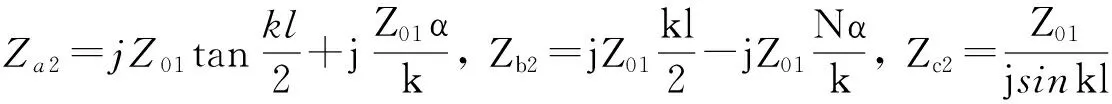
(17)

由式(17)可以看出：当D1=D2时就成为均匀截面棒的情况，α=0时其等效网络与圆锥形变幅杆一样。

3 有限元模拟

为验证文中理论的精确性，作者设计了一组中心有孔圆锥形变幅杆，将一维理论值与用有限元模拟仿真值进行比较。 材料选用 45号钢，其密度ρ=7 800 kg/m3，杨氏模E=2.06×1011N/m2，泊松系数σ=0.28。 为了便于比较，取变幅杆的长度为l=144 mm固定值。图3为中心有孔圆锥形变幅杆有限元网格图，图4为ANSYS模拟所得变幅杆位移随长度变化图，具体参数和利用 ANSYS 模拟结果见表1。表1中f1为理论计算的固有频率，f2为ANSYS软件模拟的频率，Δf1为理论计算结果与有限元分析结果比较的百分误差，M0为理论计算放大系数，M1为模拟计算放大系数，Δf2为理论计算放大系数与模拟放大系数的误差百分比。

图3 有限元网格图

图4 纵向位移随长度变化图

R1R2R3Nlf1f2Δf1M0M1Δf2522463.2514418.77618.3472.34%2.2892.2103.58%5224103.0014419.11418.4543.58%2.3152.2512.87%5224143.8014419.39218.6783.80%2.3452.2743.12%5224185.6714419.32319.0532.98%2.3792.2693.61%

由图4可计算得R1=52 mm,R2=24 mm,R3=6 mm, l=144 mm变幅杆模拟所得相应的放大系数为2.21，其他变幅杆用同样方法也可得到模拟放大系数。从表1可以看出，当变幅杆大小端及长度尺寸不变时，变幅杆理论计算频率随着中心孔径尺寸的增加而增加，理论计算放大系数也在增加。其中理论计算频率和放大系数与有限元模拟所得频率和放大系数基本一致，误差较小，都在工程应用误差范围内，表明本文理论的正确性。

4 结语

在中心有孔圆锥形变幅杆振动方程的基础上结合相应边界条件分析了频率方程及谐振长度、位移节点、放大系数、形状因数、输入力阻抗、等效网络等声学特性，同时将有限元模拟结果与理论计算结果进行对比，其结果表明理论计算频率和放大系数与有限元模拟所得频率和放大系数基本一致，误差较小。研究发现，当变幅杆大小端及长度尺寸不变时，变幅杆理论计算频率随着中心孔径尺寸的增加而增加，理论计算放大系数也在增加，其结论对中心有孔变幅杆的实际工程应用提供理论参考。

[1] 林书玉.超声换能器原理与设计[M].北京：科学出版社，2004：135-143.

[2] 贺西平，程存弟.几种常见形状函数超声变幅杆性能参量的统一表达式[J].陕西师范大学学报(自然科学版)，1994，22(3)：29-32.

[3] 贺西平，程存弟.纵振动型超声变幅杆的等效四端网络[J].陕西师范大学学报(自然科学版)，1994,22(1):87-88.

[4] 张宁宁，耿森林.幂函数扭转振动超声变幅杆研究[J].渭南师范学院学报，2013,28(6)：35-38.

[5] 周光平，李明轩.有负载的超声弯曲变幅杆振动特性分析[J].声学学报，2000，25(3)：280-284.

[6] 冯冬梅，赵福令，徐占国，等.超声波加工工具对复合变幅杆谐振性能影响[J].大连理工大学学报，2004，32(4)：685-688.

[7] 刘世清，林书玉.工具杆对超声扭转复合振动系统共振频率的影响[J].陕西师范大学学报(自然科学版)，2004，32(4):39-42.

[8] 张向慧，钱桦.1/2波长复合形变幅杆的有限元分析[J].南京理工大学学报(自然科学版)，2010，34(1)：34-37.

[9] 符卫春，孙晓清，吴胜举，等.余弦型扭转振动超声变幅杆的研究[J].声学技术，2007，26(5)：958-961.

[10] 胡新伟，贺西平，任惠娟.抗性负载常见形状变幅杆振动特性的比较[J].陕西师范大学学报(自然科学版)，2007，35(2)：55-58.

[11] 冯诺.超声手册[M].南京：南京大学出版社，1999：625-630.

[12] HUANG Y C, DING G Z, CHEN B H, et al.Simulation and experiment of langevin-type piezoelectric ultrasonic horn for micro tool motion[J].Intelligent Technologies and Engineering Systems,2013,36(9):967-974.

[13] 张云电,王纯,喻家英.中间有圆柱孔的换能器和变幅杆[J].太原机械学院学报,1993,14(3):231-237.

[14] 王维鸽,贺西平.超声纵振动空心变幅杆的特性[J].陕西师范大学学报(自然科学版),2015,43(4):43-47.

【责任编辑 牛怀岗】

Study on the Acoustic Characteristics of a Center with a Conical Horn

ZHANG Ning-ning

(School of Mathematics and Physics, Weinan Normal University, Weinan 714099, China)

The center bore round conical horn is systematically studied according to the wave equation of the longitudinal vibration of the variable section. The acoustic properties such as the frequency equation, the resonant length, the displacement node, the amplification factor, the shape factor, the input force, the equivalent network, and the acoustic characteristics have been analyzed using traditional methods. At the same time, the results of the finite element simulation are compared with the results of theory calculation. The results show that the theoretical calculation frequency and the amplification coefficient are basically the same with the finite element simulation and the amplification coefficient is basically the same. The error is small. When the horn size end and length size unchanged, horn theory calculated frequencies and theoretical calculation amplification coefficient increase with the increase of the pore size of center. The conclusion of center has hole horn practical engineering application and provides a theoretical reference.

acoustic characteristics; frequency and amplification coefficient; mechanical impedance; finite element simulation

TB553

A

1009-5128(2017)04-0044-05

2016-09-05

陕西省教育厅专项科研计划项目：介质环境对量子信息传递过程中保真度的影响(15JK1250)；渭南师范学院教育教学改革研究项目:“任务驱动探究式”教学模式在大学物理力学教学中的应用研究(JG201648)；渭南师范学院教育科学研究项目：师范生创新意识与科研能力培养(2015JYKX019)

张宁宁(1978—)，女，陕西西安人，渭南师范学院数理学院讲师，理学硕士，主要从事功率超声及声学测量研究。