一种改进型EMF谐波自适应补偿的PMSG无位置传感器控制方法

柴秀慧，张纯江，肖宏伟，赵晓君

（燕山大学电力电子节能与传动控制河北省重点实验室，秦皇岛066004）

一种改进型EMF谐波自适应补偿的PMSG无位置传感器控制方法

柴秀慧，张纯江，肖宏伟，赵晓君

（燕山大学电力电子节能与传动控制河北省重点实验室，秦皇岛066004）

提出一种改进型反电动势谐波自适应补偿的PMSG无位置传感器控制方法，该方法在滑模观测器SMO（sliding model observer）的基础上引入自适应广义二阶积分器SOGI（second order generalized integrator），减小了反电动势观测中谐波对转子位置的影响，提高了转子位置估计的准确性。由于电机参数的变化和变换器的非线性，在无位置传感器控制算法中含有大量的5、7、11次等低次谐波。使用自适应SOGI取代低通滤波器，对基频信号进行提取，一方面减小了低频谐波含量，从而减小了由低频谐波引起的转子位置估计偏差，同时消除了由滤波延时引起的相位偏差；另一方面提高了系统的跟踪性能，使得相位误差收敛于0。最后，通过仿真和实验验证了所提方法的正确性和可行性。

无位置传感器；反电动势；滑模观测器；广义二阶积分器

基于永磁同步发电机PMSG（permanent magnet synchronous）的直驱风力发电系统因其结构简单、效率较高、故障率低的特点，越来越多地出现在风力发电工业应用中［1］。转子位置的精度对直驱永磁风力发电系统性能的影响至关重要，传统检测转子位置的方法是通过位置传感器获取，但采用机械式位置传感器在不同的应用中表现出诸多问题［2-4］，如位置传感器体积增大、运行可靠性降低、安装较为麻烦、增加硬件成本等。无位置传感器技术可以解决上述问题。目前所开展的PMSG转子位置估算对象主要有：① PMSG定子磁链［5-7］；②以PMSG的电动势EMF（electromotive force）［8-9］。按照估计系统的开环和闭环可区分为两类：①开环估计，如以数学模型为基础直接推导，求取定子磁链［5,6］；②闭环估计，是在数学模型之上采样观测器实现控制，而观测器有磁链观测器［7］、滑模观测器［9］及模型参考自适应MRAS观测器和扩展卡尔曼滤波方法等。

基于定子磁链的开环转子位置估算法［5,6］模型简单，工程较易实现，动态响应快。但该算法中的纯积分环节存在零点偏移问题，需要增加补偿器校正，而且在不同电流情况下需要不同的电流补偿，但采用一阶低通滤波器、饱和积分器等方法都不能较准确地估计出转子位置。文献［7］提出基于定子磁链观测器的闭环转子位置估算法，该方法降低了定子磁链相位误差，效果有所改善，但仍不能令人满意。基于反电动势观测的无位置传感器方法是比较令人满意的算法。利用PI调节器［8］设计闭环估计反电动势，但调节器的参数设计受电机参数变化和各种测量误差的影响较大，抗扰性较差。为了提高系统鲁棒性，用滑模控制器［9］取代PI调节器对永磁同步发电机反电动势进行估计，滑模面固定，且切换由预先设置的开环函数确定，所以对参数变化和外部干扰不敏感，鲁棒性较强，算法简单。

上述的各类估算方法未考虑谐波的影响，但实际中存在诸多因素会使基波信号中包含高频干扰信号，如电机的结构不对称引起的非线性、电力电子变换器的非线性等。文献［10］对电力电子变换器的等效电阻、死区时间引起的非线性进行了分析，并提出了补偿解决方案，但其鲁棒性较差且依赖于复杂计算；文献［11］针对含高次谐波的信号引入了自适应陷波滤波器，分别滤除含量较高的若干次相应谐波，但该方法需要设计多个自适应滤波器，使得计算量增大。

本文在此基础上利用自适应广义二阶积分器取代多个陷波滤波器，降低了观测器设计的复杂程度，从而改善了由谐波引起的转子位置估算误差。

1 基于SMO反电动势转子位置估算法

PMSG的转子位置主要用于机侧变换器矢量控制坐标变换，其精度对直驱永磁风力发电系统性能至关重要。无位置传感器算法是利用机侧电流iabcs和调制电压uabcr对PMSG的转子位置进行估算，图1为基于无位置传感器控制方法的并网直驱风力发电系统控制框图，机侧变换器实现了最大风能跟踪控制,网侧变换器保证了直流母线电压恒定。

图1 并网直驱风力发电系统控制框图Fig.1 Control block diagram of grid-connected directdrive diagram wind system

PMSG在αβ坐标系下的数学模型为

式中：uαs、uβs分别为α、β轴定子端电压；iαs、iβs分别为α、β轴定子电流；Rs为定子线组的等效电阻；Ls为定子电感；eαs、eβs分别为α、β轴反电动势，即

式中：ψ0为转子磁链幅值；ωr为实际转子角速度；θr为实际转子相位。

为了对αβ坐标系下的反电动势进行观测，构造了如图2所示的滑模观测器SMO(sliding mode observer)。图中，SMO为滑模观测器的模型，SMO=1/（Lss+ Rs），F（εr）为滑模开关函数，LPF为低通滤波器，PLL为锁相环，为估算转子角速度，为估算转子相位。其输入定子端电压是由调制电压和直流母线电压合成的，即。

图2 滑模观测器框图Fig.2 Block diagram of sliding model observer

滑模函数输入εr为电流观测值与实际电流的差，即观测系统滑模曲面为

滑模开关函数F（·）的选择关系到滑模面的切换快慢和切换稳定性，为了提高滑模控制系统的稳定性和可靠性，不同开关函数有不同效果，而综合考虑快速性和抗抖振型，选择sigmoid函数，即

式中：x为函数的自变量，本文体现为εr；k为幅值参数；a为收敛参数。函数关系曲线如图3所示，从图中可以看出，a取值不同会影响函数的输出饱和速度，在设计时应综合考虑。

图3 sgmoid函数的关系Fig.3 Relationship of function of sigmoid

为了进一步确定sigmoid函数中参数k的选取和滑模观测器的稳定工作区间，可通过构造李亚普诺夫正定函数来确定，可以得出

为了补偿由低通滤波器引起的相位滞后，加入补偿相角δ，如图2所示。由于电机转速是可变的，所以δ的近似求法为

式中，ωz为低通滤波器的转折频率。

2 反电动势观测中的谐波

2.1 电机结构和参数

由永磁同步发电机的结构特点可知，当永磁磁极和定子齿距不对称时会引起转子位置产生谐波误差，其直接体现为转子磁链中含有低次谐波［7］。主要包含5次、7次谐波，这些谐波的存在将会引起转子相位偏差。

2.2 变换器的非线性

电力电子变换器工作在非线性状态，将产生一些谐波成分，再加上如IGBT参数不一致、死区时间设定等因素，这将进一步增加电路中的5次、7次等低次谐波含量。这些谐波会随着坐标变换使得矢量控制中出现含量较高的6次谐波分量。

2.3 滑模观测器

由前述可知，滑模观测器是在两个滑模曲面之间高速切换从而使得系统趋于稳定，误差趋于收敛的。具有非线性的开关函数，其输出信号含有大量谐波，谐波次数主要与开关函数的参数a选取有关。

上述3种类型的谐波体现在图2的反电动势估计值eαβs中，进一步影响转子位置估计的准确性。

3 谐波自适应补偿

改进型谐波补偿器是基于自适应SOGI滤波器而设计的，其无位置传感器框图如图4所示。滑模观测器输出的反电动势作为自适应SOGI的输入，输出的再经PLL进行相位角的提取。SOGI模型如图5所示。

图4 改进型的滑模观测器框图Fig.4 Block diagram of improved sliding model observer

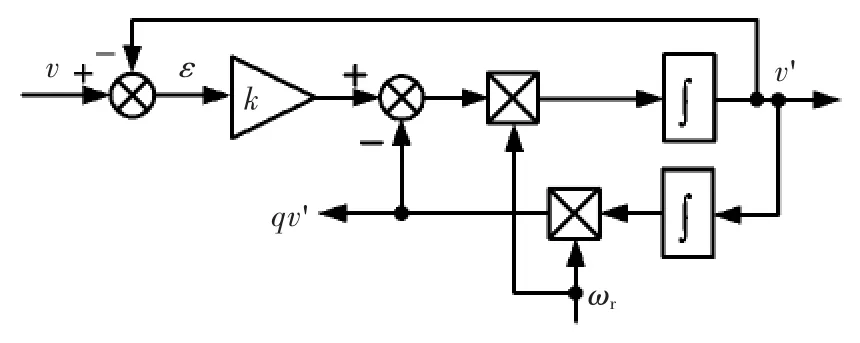
图5 SOGI模型Fig.5 Model of SOGI

由图5可知，SOGI的传递函数为

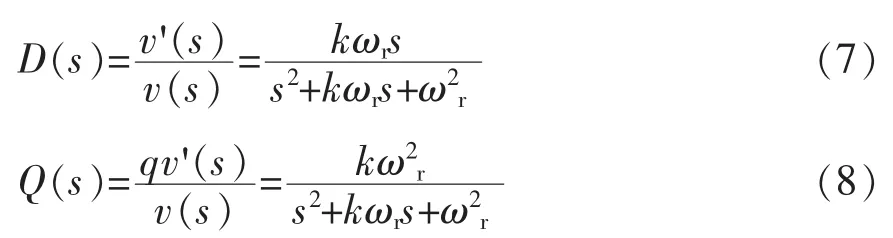
图6和图7分别为D（s）和Q（s）在不同k值时的Bode图。通过调节k值来调节两个滤波器带宽，k值越小，滤波效果越好，但其动态响应速度越慢，折中考虑，取。

图6 D（s）的伯德图Fig.6 Bode plot of D（s）

图7 Q（s）的伯德图Fig.7 Bode plot of Q（s）

4 仿真与实验

4.1 仿真验证

为了验证上述理论分析的正确性，对PMSG的无位置传感器控制方法进行仿真研究。图8为分别采用LPF和自适应SOGI作为滤波器的转子位置和相位误差仿真波形，其中风速为10m/s，相位误差θerror=θr-。由图8（a）可见，虽然采用了相位补偿，但是稳态之后依然存在固定的相位偏差，且相位误差波动较大；由图8（b）可见加入自适应SOGI，系统动态响应速度较慢，但是稳定之后，相位误差收敛于0，且相位误差波动较小。

图8 转子位置和相位误差的仿真波形Fig.8 Simulation waveforms of rotor positions and phase errors

图9为分别采用LPF和自适应SOGI作为滤波器的PMSG定子电流的总谐波失真THD（total harmonic distortion）。

图9 PMSG定子电流THDFig.9 THD of PMSG stator current

图10和图11分别为采用改进型反电动势谐波自适应补偿无位置传感器控制的PMSG系统在风速突变时，转子相位及最大功率点跟踪MPPT（maximum power point tracking）波形。当t=0.4 s时，风速由4 m/s突加为10 m/s；当t=0.7 s时，风速由10 m/s突减为6 m/s。由图10可知，随着风速的突变，估算转子位置能够很好地跟踪实际转子位置，且误差逐渐平滑收敛于0。由图11可知，随着风速的变换，系统依然可以实现了最大风能跟踪控制。上述仿真验证了改进型反电动势谐波自适应补偿的无位置传感器控制方法的可行性。

图10 风速突变下转子相位和相位误差Fig.10 Rotor position and phase error under wind speed mutation

图11 风速突变下MPPT波形Fig.11 MPPT waveforms under wind speed mutation

4.2 实验验证

为了进一步验证该无位置控制算法的正确性，本文在一台10 kW实验平台上进行了实验验证。实验中用异步电机拖动永磁同步发电机模拟风力发电系统，控制器采用TMS320F2812控制电机和变换器。实验中以光电编码器得到的转子位置作为实际转子相位。

仿真中，相位误差θerror通过运算处理折算到0附近，但是由于θerror很小，在实验中，受到干扰不容易辨识，因此，实验中不对θerror作进一步运算处理。图12给出了在本文实验中的转子实际位置角与估计位置角的比较示意，其相位误差为

图12 和θr的比较Fig.12 Comparison of and θr

图13为分别采用LPF和自适应SOGI作为滤波器的转子位置和相位误差仿真波形。图中为采用LPF的估算转子位置，为采用SOGI的估算转子位置,θerror1为采用LPF的相位误差，θerror1为采用SOGI的相位误差。从图中可以看出尽管二者均能估计出转子位置，但比偏差较小；θ 的误差error1脉冲明显为正值，说明存在固定的相位偏差，θerror2的误差脉冲有正值有负值且脉宽保持较小，说明θerror2在0附近波动，收敛更准确。同时，θerror1的脉冲宽度明显比θerror2的宽，这说明前者误差大。综上，实验表明使用自适应SOGI滤波效果较好，且不会使转子位置估算产生相位固定偏差，而是收敛于0。

为进一步验证改进方法的准确性，对不同转速和不同负载的误差进行对比，波形如图14和图15所示。

图13 转子位置和相位误差的实验波形Fig.13 Experimental waveforms of rotor position and phase errors

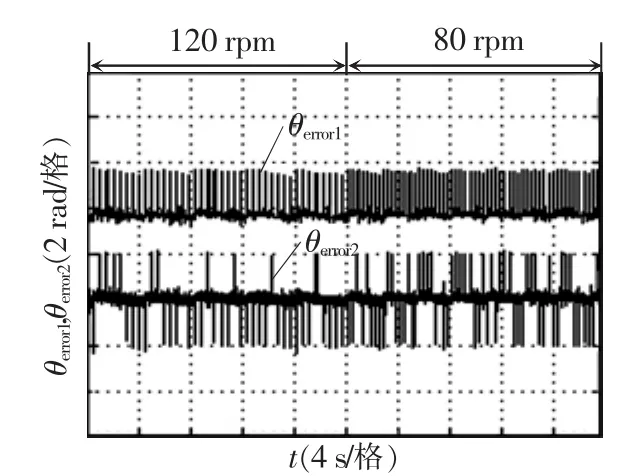
图14 变转速时相位误差比较Fig.14 Comparison of phase errors with speed changing

图15 变负载的误差比较Fig.15 Comparison of phase errors with load changing

图14为传动电机的转速从120 rpm切换到80 rpm时采用LPF和SOGI的相位误差波形对比。从图中可以看出：θerror1的误差脉冲为正值，说明超前一定角度，而且在低速时脉冲较密集，说明偏差比较大（因低转速时周期较大，而误差脉冲反而变密，由此可知误差脉冲变宽）;θerror2在转速变化时仍体现为正负交替的误差脉冲，说明收敛于0。

实验时，机侧变换器控制直流电压，图15为改变直流负载时的相位角误差比较。从图可见，不同负载时位置角误差θerror2较小，且维持在0 rad左右；虽然θerror1随着负载改变而变，但不是很大；且其误差脉冲仍偏向一个方向，说明超前θr1一个固定相位。

5 结语

本文提出一种改进型反电动势谐波自适应补偿的PMSG无位置传感器算法，该法在应用滑模观测器基础上引入自适应广义二阶积分器SOGI，减小了反电动势观测值谐波对转子位置的影响，提高了角度估计的准确性。最终，通过仿真和实验验证了该算法的正确性和准确性。

［1］季小康,廖勇.直驱风力发电系统三电平变换器控制策略研究［J］.电源学报,2014,12（2）:78-84. Ji Xiaokang,Liao Yong.Control strategy study on threelevel NPC converters of directdriven wind power generation system［J］.Journal of Power Supply,2014,12（2）:78-84（in Chinese）.

［2］贾洪平，孙丹，贺益康.基于滑模变结构的永磁同步电机直接转矩控制［J］.中国电机工程学报，2006，26（20）：134-138. Jia Hongping，Sun Dan，He Yikang.The PMSM DTC based on variable structure sliding mode［J］.Proceedings of the CSEE，2006，26（20）：134-138（in Chinese）.

［3］储剑波，胡育文，黄文新，等.永磁同步电机直接功率控制基本原理［J］.电工技术学报，2009，24（10）：21-26. Chu Jianbo,Hu Yuwen,Huang Wenxin，et al.Basic theory of direct power control for PMSM［J］.Transactions of China Electrotechnical Society，2009，24（10）：21-26（in Chinese）.

［4］Sakamoto K，Iwaji Y，Endo T.Position and speed sensorless control for PMSM drive using direct position error estimation［C］.IEEE Industrial Electronics Society Annual Conference. Denver，CO：IEEE，2001：1680-1685.

［5］Senjyu T，Tamaki S，Uezato.Vector control of permanent magnet synchronous Motors without position and speed sensors［C］.Power Electronics Specialists Conference，1995，2：759-765.

［6］Halkosaari T，Vacon O.Speed sensorless vector control of a redundant Permanent magnet wind power generator［C］. IEEE International Symposium on Industrial Electronics，2007，6：2595-2600.

［7］周扬忠，许海军.直接转矩控制永磁同步发电机相位自校正型定子磁链观测器［J］.中国电机工程学报，2012，18（32）：98-107. Zhou Yangzhong，Xu Haijun.A phase self-tuning stator flux linkage estimator forpermanent magnet synchronous generators based on the direct torque control［J］.Proceedings of the CSEE，2012，18（32）：98-107（in Chinese）.

［8］黄雷，赵光宙，年珩.基于扩展反电势估算的内插式永磁同步电动机无传感器控制［J］.中国电机工程学报，2007，27（9）：59-63. Huang Lei，Zhao Guangzhou，Nian Heng.Sensorless control of interior permanent magnet synchronous motor by estimation of an extended electromotive force［J］.Proceedings of the CSEE，2007，27（9）：59-63（in Chinese）.

［9］Hongryel K，Jubum S.A high-speed sliding-mode oserver for the sensorless speed control of a PMSM［J］.IEEE Transactions on Industrial Electronics，2011，58（9）：4069-4077.

［10］Hejny R W，Lorenz R D.Evaluating the practical low speed limits for back-emf tracking-based sensorless speed control using drive stiffness as a key metric［J］.IEEE Transactions on Industry Applications，2011，47（3）：1337-1343.

［11］Wang Gaolin，Zhan Hanlin.Adaptive compensation method of position estimation harmonic error for EMF-based observer in sensorless IPMSM drives［J］.IEEE Transactions on Power Electronics，2014，29（6）：3055-3064.

One Improved EMF Harmonic Adaptive Compensation for PMSG Sensorless Control Method

CHAI Xiuhui,ZHANG Chunjiang,XIAO Hongwei,Zhao Xiaojun
（Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei province, Yanshan University,Qinhuangdao 066004,China）

An improved back electromotive force（EMF）harmonic adaptive compensation for PMSG sensorless con-trol method was proposed in this paper,which is introduced into the adaptive second order generalized integrator（SOGI）based on sliding model observer（SMO）.This method reduces the influence of harmonic on the rotor position in back-EMF observer and improves the precision of rotor position estimation.Due to the change of the generator parameters and the nonlinearity of the converter,there is a large number of low order harmonics,such as 5th,7th,11th orders,in the sensorless control algorithm.In this paper adaptive SOGI is used to instead of LPF.The fundamental frequency signals is extracted by SOGI,on the one hand,it reduces the low frequency harmonic content,thereby reducing the rotor position estimation error caused by low frequency harmonic,while eliminating the phase deviation caused by filtering delay.On the other hand,this method improves the system tracking performance and makes the phase error converges to zero.Finally the correctness and feasibility of the proposed method is verified by simulation and experiment.

sensorless;back electromotive force（EMF）;sliding mode observer（SMO）;second order generalized Integrator（SOGI）

柴秀慧

柴秀慧（1984-），女，博士研究生，研究方向：双馈风力发电、永磁直驱风力发电、有源功率因数校正，E-mail：caixiu huihb@126.com。

张纯江（1961-），男，通信作者，博士，教授，博士生导师，研究方向：可再生能源分布式发电及控制技术、高频逆变电源及并联、并网技术、高功率因数变流及控制技术，E-mail：zhangcj@ysu.edu.cn。

肖宏伟（1989-），男，硕士，研究方向：风力发电，E-mail：hwshawysu@163. com。

赵晓君（1985-），男，博士研究生，研究方向：大功率UPS系统及其控制，E-mail：zhaoxiaojun@ysu.edu.cn。

10.13234/j.issn.2095-2805.2017.1.55

：TM 762

：A

2015-12-09

河北省高等学校科学技术研究重点资助项目（ZH2012053）

Project Supported by Science and Technology Research Key Foundation of Hebei Provice Higher Educational Institutes（ZH 2012053）