血常规项目测量不确定度和六西格玛的评定研究

陈龙梅，刘万超，刘 琪，曹大伟，王文惠，杨振华

(上海市宝山区中西医结合医院检验科，上海 201900)

血常规项目测量不确定度和六西格玛的评定研究

陈龙梅，刘万超，刘 琪，曹大伟，王文惠，杨振华△

(上海市宝山区中西医结合医院检验科，上海 201900)

目的 结合测量不确定度和六西格玛(σ)评估本实验室血液常规项目。方法 分别以质量控制数据与室间质量评价(EQA)数据和校准品评定白细胞(WBC)、红细胞(RBC)、血红蛋白(Hb)、红细胞压积(HCT)、血小板(PLT)的测量不确定度和σ，并以此计算平均红细胞体积(MCV)、平均血红蛋白浓度(MCH)、平均每升红细胞中所含血红蛋白浓度(MCHC)的测量不确定度和σ，以T检验分析EQA数据和校准品评定结果间的统计学差异。结果 评定不确定度和σ时EQA数据与校准品二者间差异无统计学意义(P>0.05)，但EQA数据评定的不确定度较校准品评定的不确定度高，而σ值校准品评定的较高。结论 测量不确定度与σ的评定可较全面地反映实验室分析中的质量。

白细胞计数；红细胞指数；血小板；数学计算；血液学实验；实验室技术和方法；测量不确定度；室间质量评价

测量不确定度是表征赋予被测量量值分散性的非负参数[1]，已在计量学上广泛使用。而六西格玛(σ)是量化实验室内部和实验室间比对结果的参数[2]，是国际上引进的一种质量管理理念和方法，已在临床实验室逐步应用[3-4]。两者均是计量学上可以通用且量化的指标，有利于实验室间比对的一致性。测量不确定度可通过分析随机误差和系统误差相关的两个不确定度分量，评定被测量量值的分散性[1]。而σ的评定可了解到实验室需要优先改善的项目和类型及改善时应采用的规则[5]。本文结合不确定度和σ分析本科室的血液常规项目。

1 材料与方法

1.1 材料 希森美康XE-2100血细胞分析仪，试剂和质控品为仪器厂家所配套，校准品为希森美康SCS-1000，批号为40620525；室间质量评价(EQA)样品来自上海市临床检验中心，批号分别为201401-201410，201501-201505。

1.2 方法

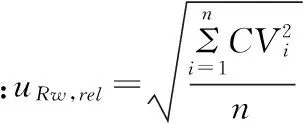
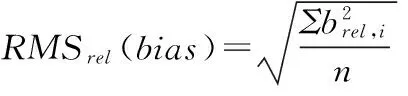
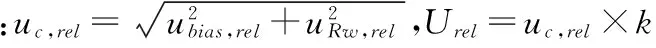
比较两种评定不确定度的方案。以统计学t检验分析高、低浓度下相对扩展不确定度。

1.2.2 6的计算和评价 根据韦斯特加氏(Westgard[7])提出的计算公式：σ=[允许总误差(TEa)-偏移(Bias)]/CV，TEa参照我国临床血液学检验常规项目分析质量要求[8]规定的允许总误差，Bias方法A为计算2014～2015年参加的EQA与靶值间差值的均值；方法B来自测量值与校准品值间bias的均值，CV来自2014年6个月的室内质控数据。当σ水平>4σ时其性能评定为“优”，3σ>σ水平>2σ时评定为“中”，σ水平<2σ时评定为“差”。低于3σ水平的检测项目需要立即采取相关措施提高其检测水平。

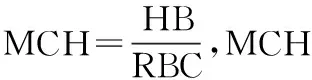
表1 高、低浓度下血常规项目的变异系数

计算MCV、MCHC的σ。

对于低于6σ的项目均需评价质量目标指数(QGI)，其计算方法为QGI=Bias/[1.5×CV]。若QGL<0.8，表明该方法需提高精密度，若QGL>1.2，表明该方法需提高正确度，若1.2>QGI>0.8，表明该方法的精密度和正确度均需要改进。

t检验统计学分析评定σ的EQA数据和校准品间统计学差异。

1.2.3 结合不确定度和 分析本实验室临床血液常规项目的质量。

2 结 果

2.1 Urel的评定

2.1.1 不精密度引入的相对不确定度 质控品分为高、低两个浓度，6个月的CV见表1。

2.1.2 Urel的计算和比较 两种方法计算的Urel差异无统计学意义(P低值=0.40，P高值=0.36)，见表2。

2.2σ的评定

2.2.1σ的计算 高低浓度下由校准和EQA获得的偏移与变异系数计算得到的σ值差异无统计学意义(P低浓度=0.45，P高浓度=0.31)，见表3。

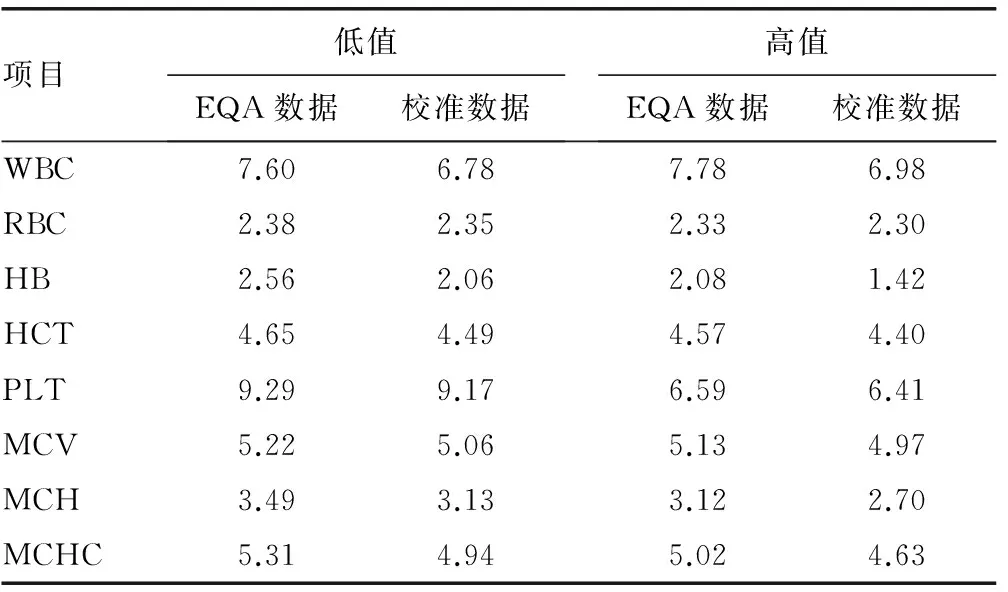
表2 两种方案计算高、低浓度下的Urel(%)

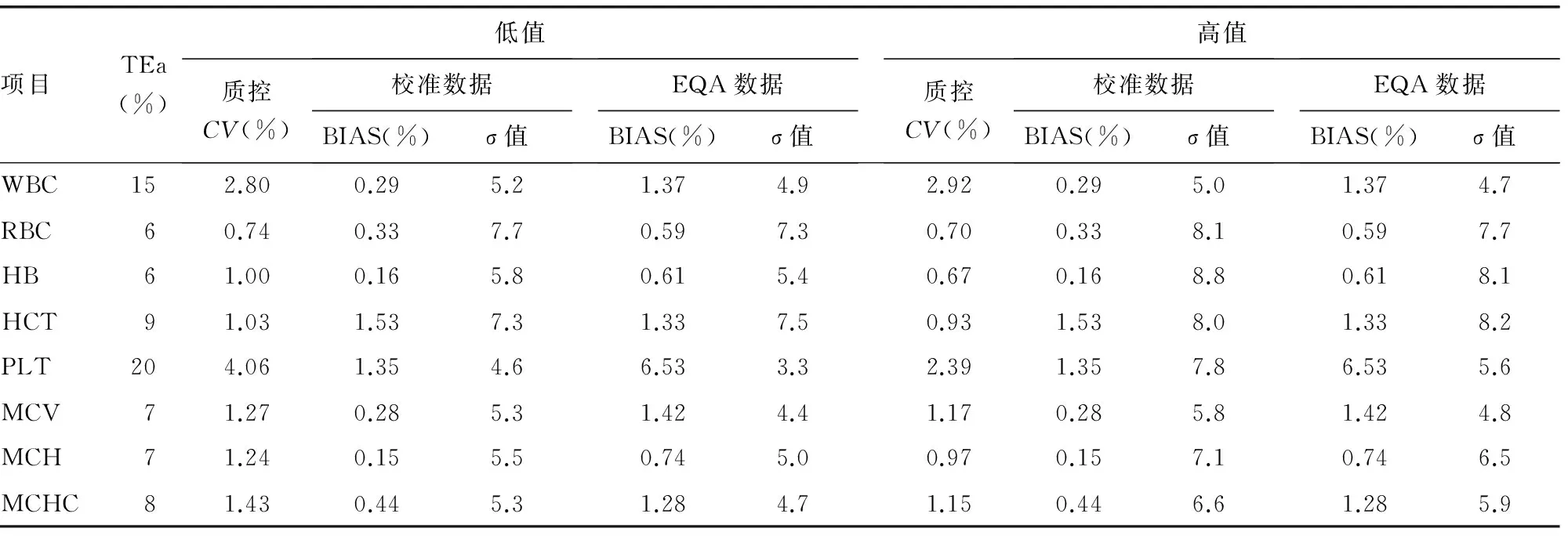
表3 高、低浓度下血液常规项目的σ值

2.2.2QGI的计算 根据公式计算QGI，高值中由校准数据得到的QGI显示WBC和MCV需改进精密度，而EQA数据计算的QGI反映WBC、MCHC需改善精密度，但PLT需要改进偏移，MCV需改进两个方面；低值中校准数据和EQA数据计算的QGI较一致，均表示WBC、HB、PLT、MCV、MCH、MCHC需要提高精密度。

3 讨 论

测量不确定度与σ在数据应用方面较为相似，但意义有所不同，本文对同血液常规项目分别评价，探讨其相同点和不同点。

EQA数据是上海市临床检验中心评定上海地区医学实验室正确度的重要参数，而校准品是正确度控制物[10]，可溯源至国际血液学标准委员会(ICSH)参考方法[11]。以3次EQA数据评价所得到的不确定度较高而σ值较低，差异无统计学意义，但由于EQA数据包含的时间跨度较校准品评定的时间长，能够更好地代表实验室的偏移，故推荐应用EQA数据评定偏移。

因质控品批号的更换对6个月的质控数据合并不精密度进行评定。医学实验室质控品更换是较常见的现象，合并不精密度更能较好地代表医学实验室长期的测量水平。本实验采用的质控数据包含了试剂批号更换，质控品批号更换，仪器校准，人员轮转等影响因素，故该6个月的质控数据能够较为真实地代表本实验室的测量不精密度水平。

与国内学者卢妙莲等[12]评定WBC、RBC、Hb、PLT高、低浓度下扩展不确定度相比，本实验扩展不确定度较小，原因可能为参加北京市卫生部临床中心EQA的实验室较多等因素引入的测量不确定度较大。国内σ大多不分高低浓度[13-14]，本文分析发现高、低浓度下的σ需要改进的质控规则有所不同，低值浓度下主要需提高精密度，而高值浓度下σ值大多超过6σ，仅需要进行13S和12.5S规则控制，本实验室提高质量主要需提高、低值浓度的不精密度水平。

测量不确定度是测量结果的不确定度[15]，与被测量量值存在测量不确定度分布图[6]，随着测量结果变化而变化。6σ是衡量整个实验室的指标，反映的是实验室的整体情况，可以用于实验室不同时间及不同实验室的质量评价。测量不确定度与被测量相关而σ与整体测量水平有关，结合两者的优势能够全面的表达实验室分析中的质量。

[1]JointCommitteeforGuidesinMetrology(JCGM).Guidetotheexpressionofuncertaintyinmeasurement[M].Switzerland:InterOrganforStandard,2008：36-37.

[2]NevalainenD,BerteL,KraftC,etal.Evaluatinglaboratoryperformanceonqualityindicatorswiththesixsigmascale[J].ArchPatholLabMed,2000,124(4):516-519.

[3]王治国．6σ质量标准在临床实验室质量控制的应用(Ⅰ)[J].上海医学检验杂志，2002,17(2)：125-127．

[4]王治国．6σ质量标准在临床实验室质量控制的应用(Ⅱ)[J].上海医学检验杂志，2002,17(3)：189-190．

[5]王治国，王薇，李少男.临床化学检验项目的σ水平的计算及质控方法的选择[J].检验医学,2009,24(1):71-73.

[6]ClinicalandLaboratoryStandardsInstitute(CLSI).Expressionofmeasurementuncertaintyinlaboratorymedicine[M].2nd.Wayne:CliniLaborStanInst,2012:13-35.

[7]WestgardJO,WestgardSA.Thequalityoflaboratorytestingtoday:anassessmentofsigmametricsforanalyticqualityusingperformancedatafromproficiencytestingsurveysandtheCLIAcriteriaforacceptableperformance[J].AmJClinPathol,2006,125(3):343-354.

[8]中华人民共和国卫生部.WST406-2012临床血液学检验常规项目分析质量要求[M].北京：中国标准出版社,2012:7.

[9]CoskunA.Sixsigmaandcalculatedlaboratorytests[J].ClinChem,2006,52(4):770-771.

[10]中国合格评定国家认可委员会.医学实验室-测量不确定度的评定与表达[M].北京：中国计量出版社,2012:28-47.

[11]彭黎明，邓瑞雪．血细胞自动分析校准的溯源[J]．中华检验医学杂志，2005，28(5)：475-477．

[12]卢妙莲，胡珺，高云龙，等．血液常规检验项目测量不确定度评定[J]．实用医学杂志，2014(11)：1817-1819．

[13]谭晓霞，兰蔚蔚，徐晓红，等．6σ理论在评价临床实验室血液分析各阶段性能及设计质控方案中的应用[J]．检验医学，2012，27(1)：63-66．

[14]吴晓华，苏凌云，李秋晨，等．运用6σ评价急诊血液项目各检测阶段的性能[J]．检验医学，2013，12(12)：1132-1136．

[15]王惠民，季伙燕．医学检验中应该评定“测量程序”还是“测量结果”的不确定度[J]．临床检验杂志，2011,28(5)：324-326．

陈龙梅(1988-)，检验师，硕士，主要从事实验室质量控制方面研究。△

�验交流·

10.3969/j.issn.1671-8348.2017.02.030

R446.11+1

B

1671-8348(2017)02-0239-03

2016-07-16

2016-10-12)