炭质泥岩软弱夹层岩质边坡稳定性影响因素分析

刘新喜, 戴毅, 张平, 侯勇, 江佳



炭质泥岩软弱夹层岩质边坡稳定性影响因素分析

刘新喜, 戴毅, 张平, 侯勇, 江佳

(长沙理工大学土木与建筑学院, 湖南长沙, 410004)

为探究软弱夹层对岩质边坡稳定性的影响规律, 采用自编的强度折减程序对多种工况下单因素变化的边坡稳定性进行了数值计算, 并通过极差分析法设置正交试验对边坡稳定性多因素敏感性展开了分析。结果表明: 软弱夹层空间位置分布和抗剪强度指标对边坡稳定性影响程度依次为软弱夹层的倾角、内摩擦角、黏聚力、厚度; 当软弱夹层的倾角在25°～60°范围内变化时, 边坡的安全系数变化曲线大致呈开口向上的抛物线, 抛物线顶点位于软弱夹层45°倾角处, 此时边坡的稳定性最差, 在实际工程中应特别注意此类软弱夹层边坡的失稳问题。

软弱夹层; 边坡稳定性; 敏感性分析

边坡稳定性影响因素分析一直以来都是学者和工程师们研究的热点。张德佳[1]、王志勇[2]采用FLAC3D数值模拟软件, 以边坡坡高、坡角, 夹层黏聚力、摩擦角、倾角为变量因素, 研究了变量单因素对软弱夹层岩质边坡变形和稳定性的影响规律。秦鸿[3]从边坡坡高、坡角, 软弱夹层倾角、黏聚力和内摩擦角对含软弱夹层岩质边坡的位移影响规律进行了量化研究, 并通过多因素综合分析探讨了这几类影响因素在工程中判别边坡稳定性的实际意义。吕博[4]首次引入软弱夹层与坡角之间的距离因子来分析边坡变形和稳定性的相关规律, 结果表明边坡安全系数随着软弱夹层与坡角距离的增大而逐渐增大。罗聪[5]选取软弱夹层埋深和内摩擦角2个因素, 研究了坡底水平状软弱夹层岩质边坡稳定性, 结果表明: 当软弱夹层埋深较浅时, 坡体滑动面沿软弱夹层形成, 边坡稳定性迅速下降; 当软弱夹层埋深增大到一定程度时, 坡体滑动面将不经过软弱夹层且呈圆弧形, 这种情况下软弱夹层对边坡稳定性的影响可以忽略。蒋昱州等[6]通过FLAC3D数值分析软件模拟了软弱夹层间距、长度、厚度、倾角和岩桥倾角等因素对边坡变形的影响规律, 结果表明, 软弱夹层的长度、间距和厚度对边坡变形影响较大, 软弱夹层倾角和岩桥倾角则对边坡变形影响较小。

综上所述, 国内外关于软弱夹层对边坡稳定性影响的研究成果主要集中在影响规律方面, 而对影响因素的敏感性程度分析较为欠缺, 且对软弱夹层厚度的研究重视程度还不够, 事实上软弱夹层的厚度对边坡稳定性有着重要影响。鉴于此, 本文设置多种工况对单因素变化的边坡稳定性进行数值计算后, 进一步采用极差分析法设置正交试验对影响因素的敏感性展开分析, 为炭质泥岩软弱夹层岩质边坡稳定性的分析和设计提供理论依据。

1 模型的建立

采用理想弹塑性本构模型和摩尔-库伦强度屈服准则[7–8], 运用自编的强度折减程序进行边坡稳定性数值计算。

边坡有限元力学模型的建立应在保证实际边坡特性的前提下, 尽量简化模型以方便模型的建立及计算分析。炭质泥岩软弱夹层岩质边坡稳定性影响因素分析的力学计算模型如图1所示。边坡高50 m, 软弱夹层倾角的范围为30°～39°, 软弱夹层厚度为2.5～4 m, 夹层厚度变化时保持上覆岩体重量不变。软弱夹层倾角变化时, 边坡坡顶与软弱夹层前沿的距离取10 m, 坡顶以下取6 m。为防止运算过程中边坡底部约束对软弱夹层及边坡位移的影响, 边坡底部设置较大的路基层区域, 基层厚80 m, 长150 m,方向取4 m。

图1 计算模型

2 材料参数和计算工况

2.1 基本物理力学参数

边坡岩体由大理岩和炭质泥岩组成, 其物理力学参数如表1所示。

表1 边坡各岩层物理力学参数

2.2 计算工况

对于含有软弱夹层的边坡而言, 软弱夹层的空间分布位置如夹层倾角、厚度, 抗剪强度指标如夹层黏聚力、内摩擦角共同控制着边坡的整体稳定性。针对软弱夹层边坡变形问题, 结合常见边坡特征, 考虑软弱夹层各影响因素, 拟定的4种计算工况见表2。各工况设置原则为: 固定考虑4因素的3个, 变化另1个因素, 从而获取单因素变化对边坡稳定性影响规律。重点计算各因素对坡体、方向位移最大值和边坡整体稳定系数的影响。为便于分析, 位移均取绝对值。

表2 各计算工况炭质泥岩软弱夹层参数设置 工况厚度/m倾角/(°)黏聚力/kPa内摩擦角/(°) 12.5392510～25* 22.53925～40*10 32.530～39*2520 42.5～4.0*392520 注: “*”表示变量因素。

3 炭质泥岩软弱夹层岩质边坡稳定性分析

3.1 夹层内摩擦角对边坡位移和安全系数的影响

工况1的边坡位移最大值和安全系数计算结果如图2所示。

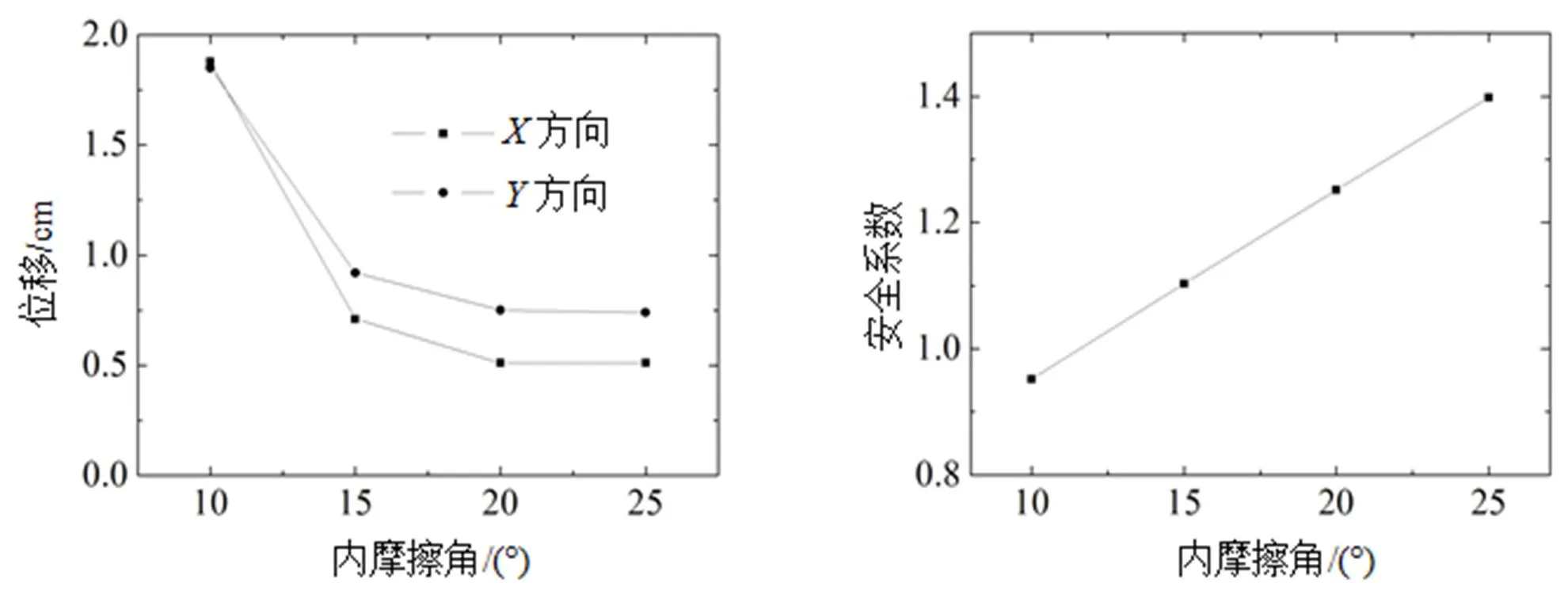
图2 软弱夹层不同内摩擦角的边坡位移最大值和安全系数变化规律

从图2可知: 边坡、方向最大位移随软弱夹层内摩擦角的增大而减小, 但软弱夹层内摩擦角对边坡最大位移的影响并非单一线性关系, 而是呈指数函数变化; 边坡安全系数随软弱夹层内摩擦角的增大而线性增大。

3.2 夹层黏聚力对边坡位移和安全系数的影响

工况2的边坡位移最大值和安全系数计算结果如图3所示。

图3 不同夹层黏聚力下边坡位移最大值和安全系数的变化规律

从图3可知: 随着软弱夹层黏聚力的增加, 边坡最大位移以指数函数形式减小, 其规律和软弱夹层内摩擦角对边坡、方向最大位移的影响类似; 边坡安全系数随软弱夹层黏聚力的增加而线性增大。

3.3 夹层倾角对边坡位移和安全系数的影响

工况3的边坡位移最大值和安全系数计算结果如图4所示。

图4 不同夹层倾角下边坡位移最大值和安全系数变化规律

从图4可知: 与软弱夹层内摩擦角和黏聚力影响边坡变形规律不同, 软弱夹层倾角变化对边坡变形影响较大, 随着倾角增大, 边坡最大位移并没有呈指数函数形式减小, 而是表现为折线型增大; 对于边坡安全系数, 则是随软弱夹层倾角增加而线性减小, 但减小的单调性比软弱夹层内摩擦角和黏聚力的影响明显要弱。

3.4 夹层厚度对边坡位移和安全系数的影响

工况4的边坡位移最大值和安全系数计算结果如图5所示。

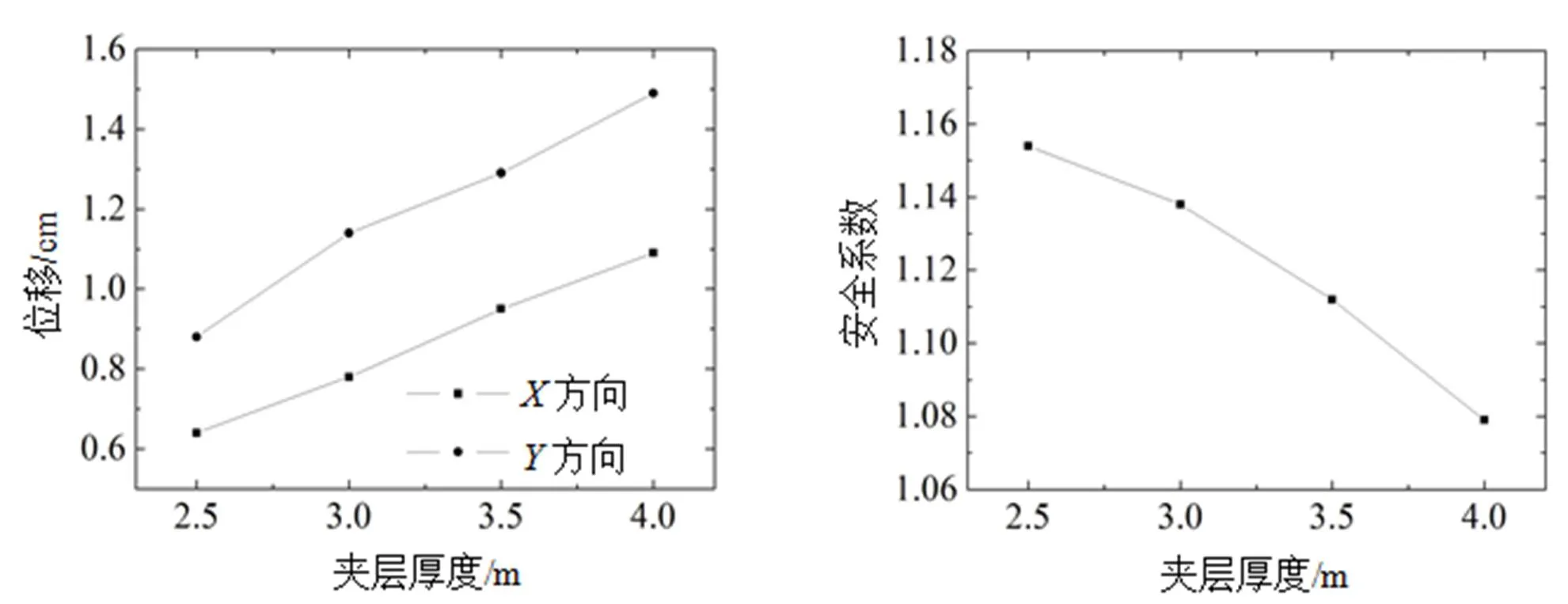
图5 不同夹层厚度下边坡位移最大值和安全系数变化规律

从图5可知: 随着软弱夹层厚度的增大, 边坡最大位移呈直线线性增加, 且边坡、方向最大位移值几乎同步变化; 对于边坡安全系数, 则随着夹层厚度增大而缓慢减小, 但减小的幅度很小。

4 影响因素敏感性分析

4.1 正交设计方法

多因素敏感性分析最简单有效的方法是正交设计法, 它基于正交原理通过试验筛选出具有代表性的个别试验数据进行敏感性分析。本文采用极差分析法对正交设计方案试验结果进行处理, 所谓极差就是平均效果中最大值和最小值之差, 通过分析每一因素的平均极差, 找到影响指标的主要因素, 进而找到最佳因素水平组合。

4.2 影响因素与水平

由于软弱夹层的空间位置分布和抗剪强度指标对边坡稳定性影响较大, 因此, 按照4因素3水平制定正交设计表L934, 对软弱夹层边坡稳定性多因素敏感性展开分析。根据室内试验获得的土工参数及通过现场调查收集的边坡几何特征, 给出敏感性分析的影响因素及其水平如表3所示。

表3 影响因素及其水平 水平厚度/m倾角/(°)黏聚力/kPa内摩擦角/(°) 12.5322010 23.0353020 33.5384030

4.3 计算方案及结果分析

根据正交试验设计方法中的正交原理, 软弱夹层的4个影响因素相互独立。将正交试验中4个因素和3个水平的试验次数记为L9Y34Y, 即本次试验最少要进行9次。通过L9Y34Y正交设计表即可确定正交试验的具体方案, 在此基础上, 再对这9个方案的边坡安全系数分别展开计算。具体试验方案和计算结果如表4所示。

表4 正交试验方案及计算结果 试验序号厚度/m倾角/(°)黏聚力/kPa内摩擦角/(°)安全系数 12.53220100.903 22.53530201.484 32.53840301.273 43.03230301.892 53.03540101.166 63.03820200.672 73.53240201.750 83.53520301.203 93.53830100.790

采用极差分析法对表4中的计算结果进行处理, 得到影响因素的敏感性分析结果见表5。极差分析法处理计算结果的流程为: 首先确定影响因素在水平下的试验平均值T; 再依次计算各影响因素在不同水平下的试验结果平均值; 最后计算每个影响因素的极差R, 以此作为评价影响因素敏感性大小的指标。试验平均值T、极差R的计算方式分别为:T为因素试验结果的和与水平数的比;R= max{1j,2j, …,Tj} – min{1j,2j, …,T}。

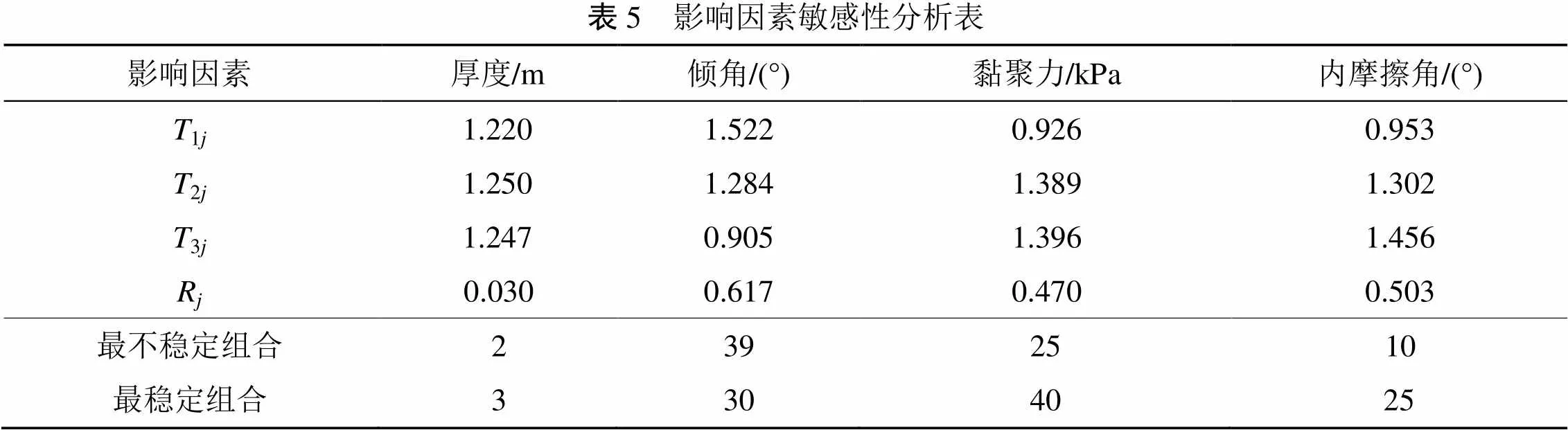
表5 影响因素敏感性分析表 影响因素厚度/m倾角/(°)黏聚力/kPa内摩擦角/(°) T1j1.2201.5220.9260.953 T2j1.2501.2841.3891.302 T3j1.2470.9051.3961.456 Rj0.0300.6170.4700.503 最不稳定组合2392510 最稳定组合3304025

通过正交试验结果表5可知, 炭质泥岩软弱夹层边坡稳定性的多因素敏感性影响程度由大到小依次为夹层的倾角、内摩擦角、黏聚力、厚度。在厚度适中时, 炭质泥岩软弱夹层的黏聚力和内摩擦角越大, 倾角越小, 越有利于边坡的整体稳定, 这与边坡现场实际情况相符。

4.4 软弱夹层倾角对边坡稳定性的影响规律

考虑到炭质泥岩软弱夹层的4个因素中夹层倾角敏感性最大, 因此就软弱夹层倾角对边坡稳定性影响规律展开进一步研究。分别取软弱夹层倾角为25°、35°、45°、55°、60°, 固定边坡高度、坡角、黏聚力、内摩擦角、软弱夹层距坡顶距离和炭质泥岩软弱夹层厚度分别为50 m、75°、30 kPa、20°、10m和2.5 m。将上述数据代入自编的强度折减法中, 求得不同倾角而其它参数相同时的边坡安全系数经整理后见图6。

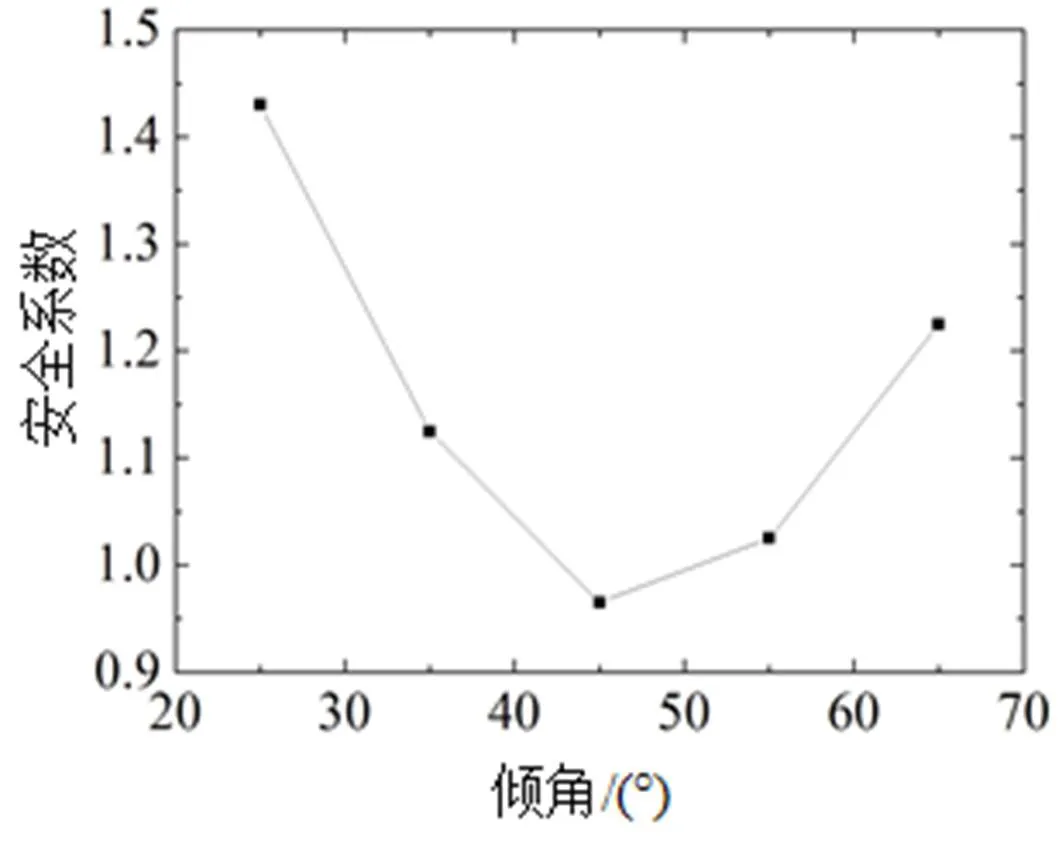
图6 不同软弱夹层倾角下边坡的安全系数

从图6可知, 当软弱夹层的倾角在25°～60°范围内变化时, 边坡的安全系数变化曲线大致呈开口向上的抛物线。当软弱夹层的倾角在25°～45°范围变化时, 边坡安全系数随夹层倾角增大而迅速降低; 当软弱夹层的倾角在45°～60°范围变化时, 边坡安全系数随夹层倾角增大而缓慢升高。抛物线的顶点位于软弱夹层45°倾角处, 此时边坡的安全系数最小(小于1), 表明此时边坡处于失稳状态, 在实际工程中应特别注意此类软弱夹层。

5 结论

为弄清软弱夹层对岩质边坡稳定性的影响规律, 本文设置多种工况对单因素变化的边坡稳定性进行了研究, 并进一步采用极差分析法设置正交试验对影响因素的敏感性进行分析, 得到如下结论。

炭质泥岩软弱夹层抗剪强度指标黏聚力和内摩擦角对边坡位移和安全系数的影响规律极为相似。炭质泥岩软弱夹层空间位置分布与抗剪强度指标对边坡位移和安全系数的影响呈现明显不同的规律, 软弱夹层倾角对边坡、方向最大位移和安全系数的影响均呈折线型变化; 软弱夹层厚度对边坡、方向最大位移的影响呈直线型变化, 而对安全系数的影响很小。

炭质泥岩软弱夹层边坡稳定性的多因素敏感性影响程度由大到小依次为夹层的倾角、内摩擦角、黏聚力、厚度。当厚度适中时, 炭质泥岩软弱夹层的黏聚力和内摩擦角越大, 倾角越小, 越有利于边坡的整体稳定。

随着炭质泥岩软弱夹层倾角的增加, 边坡的安全系数先减小后增大。软弱夹层的倾角在45°附近时, 边坡稳定性最差, 安全系数最小, 遇到此类软弱夹层边坡, 应特别引起注意。

[1] 张德佳. 含软弱夹层岩质边坡及加固效应研究[D]. 重庆: 重庆交通大学, 2010.

[2] 王志勇. 含软弱夹层岩质边坡稳定性分析研究[D]. 长沙: 中南大学, 2004.

[3] 秦鸿. 软弱夹层边坡变形性状及其影响因素分析[J]. 重庆交通大学学报(自然科学版), 2011, 30(2): 282–286.

[4] 吕博. 含软弱夹层的岩质边坡稳定性研究[D]. 邯郸: 河北工程大学, 2013.

[5] 罗聪, 袁伟民, 胡盛明, 等. 坡底软弱夹层对岩质边坡稳定性的影响[J]. 西北大学学报(自然科学版), 2010, 40(z1): 127–131.

[6] 蒋昱州, 徐卫亚, 朱杰兵, 等. 含断续软弱夹层岩石流变力学特性研究[J]. 长江科学院院报, 2009, 26(12): 71–75.

[7] 郭诚谦. 有软弱夹层岩体边坡稳定分析安全系数的确定[J]. 水利水电技术, 1995(3): 27–31.

[8] 陈新泽, 唐辉明, 杨有成, 等. 基于FLAC3D强度折减法滑坡三维稳定性研究[J]. 水文地质工程地质, 2008, 35(2): 24–29.

(责任编校: 江河)

Analysis of influencing factors of rock slope stability in weak interlayer of carbonaceous mudstone

Liu Xinxi, Dai Yi, Zhang Ping, Hou Yong, Jiang Jia

(School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410004, China)

In order to investigate the influence of weak interlayer on the stability of rock slope, the self-made intensity reduction program is used to numerically calculate the slope stability of single factor change under various working conditions. Additionally, the sensitivity of multi-factors to slope stability is analyzed by the method of range analysis. The results show that the spatial distribution of the weak intercalated layer and the shear strength index have the influence on the slope stability in the order of inclination angle, internal friction angle, cohesion and thickness. When the inclination of the weak interlayer is in the range from 25° to 60°, the slope of the safety factor of the slope is roughly upward parabola, and the parabolic apex is located at 45° of the weak interlayer. In this case, the stability of the slope is the worst, and the instability of such weak interlayer slope should be paid special attention in practical engineering.

weak interlayer; slope stability; strength reduction method; range analysis method; sensitivity analysis

10.3969/j.issn.1672–6146.2017.01.015

U 416.1+4

A

1672–6146(2017)01–0065–05

刘新喜, liuxinxi1963@126.com。

2016–11–10

国家自然科学基金(51378082, 51674041)。