设计有价值的操作活动，发展空间观念

张文兵

摘 要：发展空间观念离不开操作活动。有价值的操作活动，能激发学生的内在需要，使其产生操作的积极情感。有价值的操作活动，能在操作中结合想象，能让学生关注操作背后的数学内涵，主动将知识从肤浅走向深入。有价值的操作活动，能将积累的感性经验内化为理性认识。

关键词：空间观念；操作活动；想象

前不久参加一次教研活动，一位教师执教《长方体和正方体表面的展开图》，下面是其中的一个片段：

【案例1】

师：把一个正方体，沿着有红线的棱剪开，就可以得到正方体的展开图。你也想试一试吗？

学生操作。

师：我们将正方体沿棱剪开，得到的平面图形就是正方体表面的展开图。

师：如果沿其他的棱剪开会得到怎样的展开图呢？自己试一试吧。

学生操作。教师将不同的展开图陆续展示在黑板上。（一共3种）

师：同学们都剪完了，还有不一样的吗？

师：其实，正方体还有其他的展开图。（师将其他8种展开图展示在黑板上）

师：能把这些展开图分类吗？

学生面面相觑，课堂鸦雀无声。

师：我们可以把这11种展开图分成4类。

课件出示分类情况。

……

思考：

《长方体和正方体表面的展开图》是苏教版数学六年级上册的教学内容。案例1是例3的教学，学生将正方体沿棱剪开得到展开图，并在教师的引导下完成展开图的分类。课堂上，学生操作得十分“热闹”。然而，这番“热闹”的场景引发了笔者的思考。

1. 教材意图是什么？

传统的教材中，立体图形的展开图没有作为一个单独的内容进行教学，只是在教学表面积时，作为一种理解表面积意义的方式简单介绍一下。为什么新教材要将其单列为一课时呢？有研究表明，三维图形与二维图形的相互转化是培养学生空间观念的主要途径。《数学课程标准》也把几何体与其展开图之间的转化作为空间观念的一个内容，把能进行这些转化作为空间观念的一种表现。因此，例3的教学，是让学生通过操作活动，在经历由“体”到“形”的转化过程中获得空间观念的发展。

2. 这样操作有效吗？

案例1中，教师提供足够的时间和空间，让每一位学生都能动手操作，说明教师十分重视让学生在操作中获得对知识和方法的理解。可是，实际效果如何呢？从课上学生的表现可以看出，他们对展开图的认识是零散的，没能建构清晰的表象，导致不能有效地调动表象展开想象，进而在判断平面图形能否折叠成正方体时只能依赖折纸。这是什么原因呢？仔细分析学生的操作，就会发现，两次操作只是简单、随意地让学生“做手工”，没有明确的目的和方法的指导，也没有理性的思考和有效的交流。这样，必然不能帮助学生建构知识、深化认识，更谈不上数学能力和空间观念的发展。

3. 剪不出来怎么办？

正方体的展开图按照图形的特点可以分成4类，共11种。即：6种“1-4-1型”，3种“2-3-1型”，1种“3-3型”和1种“2-2-2型”。仅通过学生的操作，很难把这些类型的展开图都“剪”出来，那该如何处理呢？曹培英教授指出：在小学，空间观念以空间表象为主要表征形态，也包括一定的命题表征，并涉及空间知觉与初步的空间想象。①探索正方体的11种展开图，有利于提升学生的空间知觉，丰富学生的空间表象。观察、比较不同的展开图，发现它们之间的联系，是训练学生空间想象能力的重要途径。因此，教学中应选择合适的方式，使学生认识正方体的各种展开图。

基于这些思考，笔者进行了下面的教学实践。

【案例2】

1. 问题导入

师：今天老师给大家带了一个礼物，礼物就装在这个正方体的纸盒里，现在想把礼物拿出来，又不想将盒子弄坏，有什么办法吗？

生：可以剪开前面的3条棱。

师：这个方法不错，就这么剪。（教师剪开，发现里面什么也没有）

师：老师跟你们开了一个玩笑。尽管盒子里没有东西，但今天我们就要利用正方体的盒子学习很有用的知识。想学习吗？

生：想。

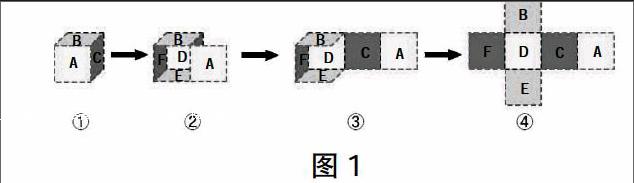
师：细心的同学可能已经发现，盒子里面写着字母。（教师按照图1剪开）

师：为了方便研究，我们就用这些字母来表示每个面。

师：我们将正方体沿棱剪开，得到一个由“6个面”连接的平面图形，这就是正方体表面的展开图。

2. 剪展开图

师：正方体表面的展开图还会有其他不同的形状吗？

生1：六个面连在一起的形状很多，肯定不止这一种。

生2：我觉得如果沿其他的棱剪开，得到的展开图可能会不一样。

生3：是的，如果按图1中的②先剪开E和F连接的棱，再剪开F和D连接的棱，得到的展开图就不一样了。

师：你们的猜想对吗？正方体除了这个展开图，还有其他形状的展开图吗？让我们带着问题去剪一剪。先看操作建议：

（1）沿着正方体的棱剪，但不能剪散。

（2）把A面当作前面，B面当作上面，固定正方体的位置，不要随意转动。

（3）边剪边想象，并用小正方形把想象的展开图拼出来。

（4）剪的过程中，如果发现原来摆的展开图不对，及时调整。

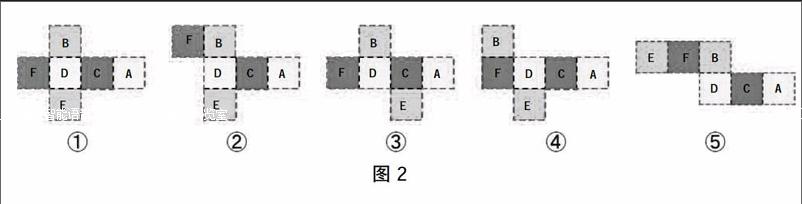
学生先想象再操作，教师巡视，将不一样的展开图（如图2）展示在黑板上。

3. 建立联系

师：图2中的这些图形有什么相同和不同的地方？

生1：五个图形D、C、A都连在一起，其中①③④中F、D、C、A连在一起。

生2：①②④中E的位置一样，都和D相连，在它的下面。

生3：①②③⑤中B的位置一样，都和D相连，在它的上面。

生4：①中F和D连接的棱没有剪开，②中F和B连接的棱没有剪开，这两个展开图只有F的位置不相同。

生5：③和④中B和E的位置不相同，因为③是B和D连接的棱没有剪开，E和C连接的棱没有剪开，而④是B和F连接的棱没有剪开，E和D连接的棱没有剪开。

生6：我发现图2中的展开图都剪开了A和B、E、F连接的棱，所以A的位置都相同。

师：能发现展开图的这么多联系，真了不起！

4. 补充展开图

师：正方体还有其他的展开图吗？

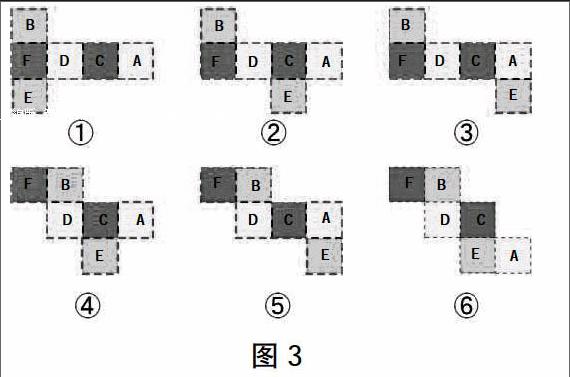
生：我觉得还应该有其他的展开图。例如，图2中的②剪开E和D连接的棱，不剪E和C连接的棱，那展开图中E就在C的下面（如图3中的④）。

师：是这样吗？我这边正好有这么一张图，谁来折折看，检验他的说法。

师：正方体的展开图的确还有其他的类型。（出示图3）

师：这些图形能折回正方体吗？先想象着折。

学生想象。

师：都能折回吗？从学具袋里选出这些图形折一折。

学生活动。

5. 分类

师：这么多的展开图，能给它们分类吗？

生1：我把图2中的①②④和图3中的①②③分成一类，把图2中的②和图3中的④⑤也分成一类，然后剩下两个分成一类。

生2：我觉得剩下的两个应该分成两类，因为它们很不一样。

师：我们就把这些展开图分成四类。

……

反思：

学生参与操作活动，在“动手做”的过程中积累基本活动经验，是发展空间观念的有效方式。因此，设计有价值的操作活动是发展空间观念的关键。那么，如何设计有价值的操作活动呢？通过教学实践，笔者对这个问题有了一些的认识。

1. 操作前，问题驱动，明确意图

有价值的操作活动，应该激发学生的内在需要，让学生带着明确的意图操作，使学生产生操作的积极情感。在操作之前，让学生思考：“正方体还会有不同形状的展开图吗？”一方面，调动学生的已有经验与新知对接，为进一步学习提供有力的操作经验与想象经验的支撑。另一方面，明确操作重点，使学生意识到操作的目的不只是要剪出一个展开图，而是怎样剪能剪出不一样的展开图，促使学生每剪一刀，都要思考“这条棱能不能剪？剪了之后会不会不一样？”这样设计，让学生内在的需求和积极的思考点燃了操作的热情，在明确意图的指引下获得了更丰富、更深刻的认知体验，发展了空间观念。

2. 操作中，结合想象，深化认识

想象是学生学习“图形与几何”领域知识的重要方法，在操作中结合想象，能让学生关注操作背后的数学内涵，主动使经验从肤浅走向深入。操作时，学生根据剪的情况想象展开图的样子，是在运动中想象，促使学生排除操作中的干扰因素，专注于发现正方体的面的运动规律，并根据发现的规律主动展开想象。这样“想象——操作——再想象”的过程是发展学生动态形象思维的重要依托。同时，以想象制造的认知冲突引发操作，又以操作制造的认知冲突展开新的想象，随着操作的不断深入，学生的思维逐步深化，建立的表象逐渐具体、生动，空间想象能力得到有效提升。

3. 操作后，交流内化，提升经验

学生在操作中积累了丰富的感性经验，需要通过交流将这些经验内化为理性认识。剪出了不同的展开图后，笔者没有急于出示其他的展开图，而是让学生交流是怎样得到这些展开图的。在经验的分享和碰撞中，学生发现了展开图中“面”的位置与剪开的“棱”的关系，不仅深入理解了剪开不同的棱会得到不一样的展开图，还能想象出剪开这些棱会得到怎样的展开图。在此基础上，出示其他的展开图并分类。这样，学生头脑中建构的展开图的表象彼此相互联系，成为一个结构化的整体，积累的由“体”到“形”转化的经验更加丰富、深刻，空间观念就在潜移默化中得到发展。

总之，发展空间观念离不开有价值的操作活动。教师要提供足够的时间和空间，使学生在活动中体验、感悟、思考、积累、内化，不断将感性经验上升为理性认识，让空间观念在知识的习得和能力的发展中得到提升。