对两道上海高考题的一点思考
许 文
(华中科技大学附属中学 430074)
平抛运动是一种典型的曲线运动.将平抛运动模型与斜面模型相结合,这是常见的一种深化平抛运动的构题方式,备受高考的关注.上海高考试题中有两道关于平抛运动与斜面相结合的问题,值得思考与探讨.
试题1 (2012上海)如图1所示,斜面上a、b、c三点等距,小球从a点正上方O点抛出,做初速度为v0的平抛运动,恰好落在b点.若初速度变为v,其落点位于c点.则( ).
A.v0
参考答案给出选项A正确.但仔细思考就会发现这个答案不准确.实际上v的范围比选项A给出的范围要小些.
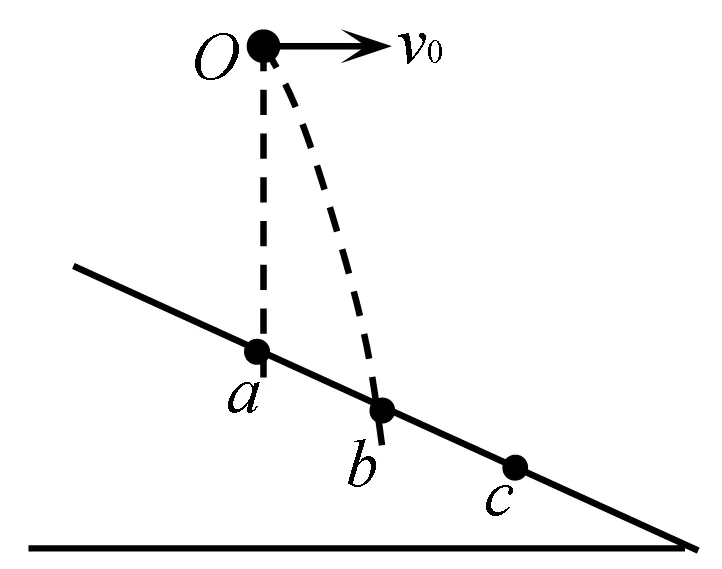
图1
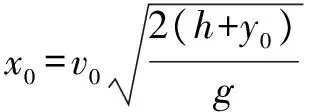
评析本题中小球平抛落在斜面上的落点位置虽然一定,但抛出点O与a点的距离h及a、b、c三点的竖直距离y0是未知的,其比值h/y0应在区间(0,∞)内.我们据平抛运动的规律将初速度v用比值h/y0来表达,即用变量h/y0来表达关于v的函数,再根据变量的定义域求函数的值域,这是利用数学知识解决物理问题的一种方法与手段.
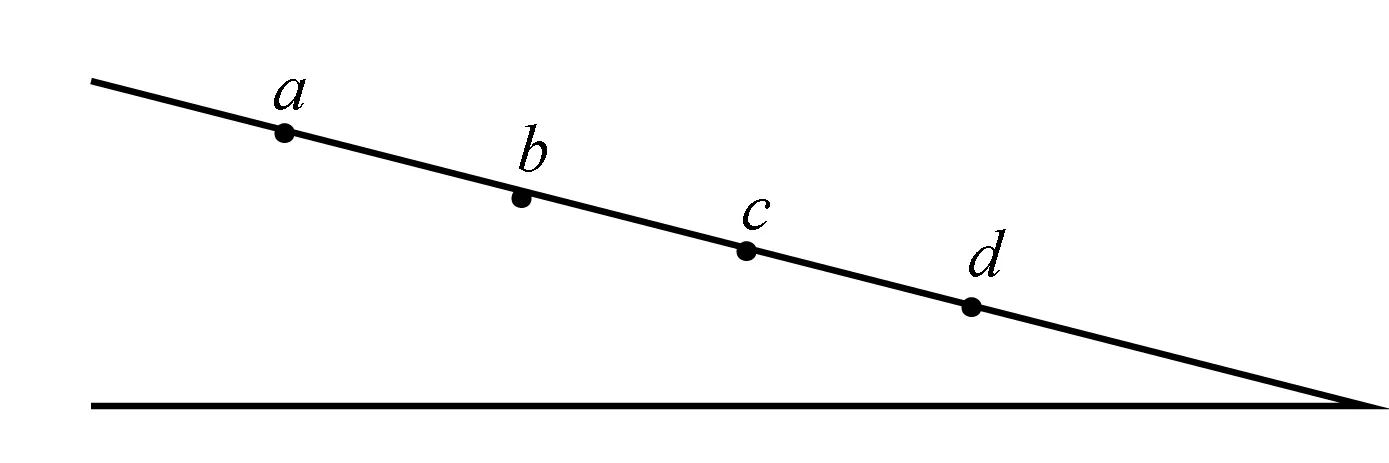
图2
试题2 (2015上海)如图2,战机在斜坡上方进行投弹演练.战机水平匀速飞行,每隔相等时间释放一颗炸弹,第一颗落在a点,第二颗落在b点.斜坡上c、d两点与a、b共线,且ab=bc=cd,不计空气阻力.第三颗炸弹将落在( )
A.bc之间 B.c点 C.cd之间 D.d点
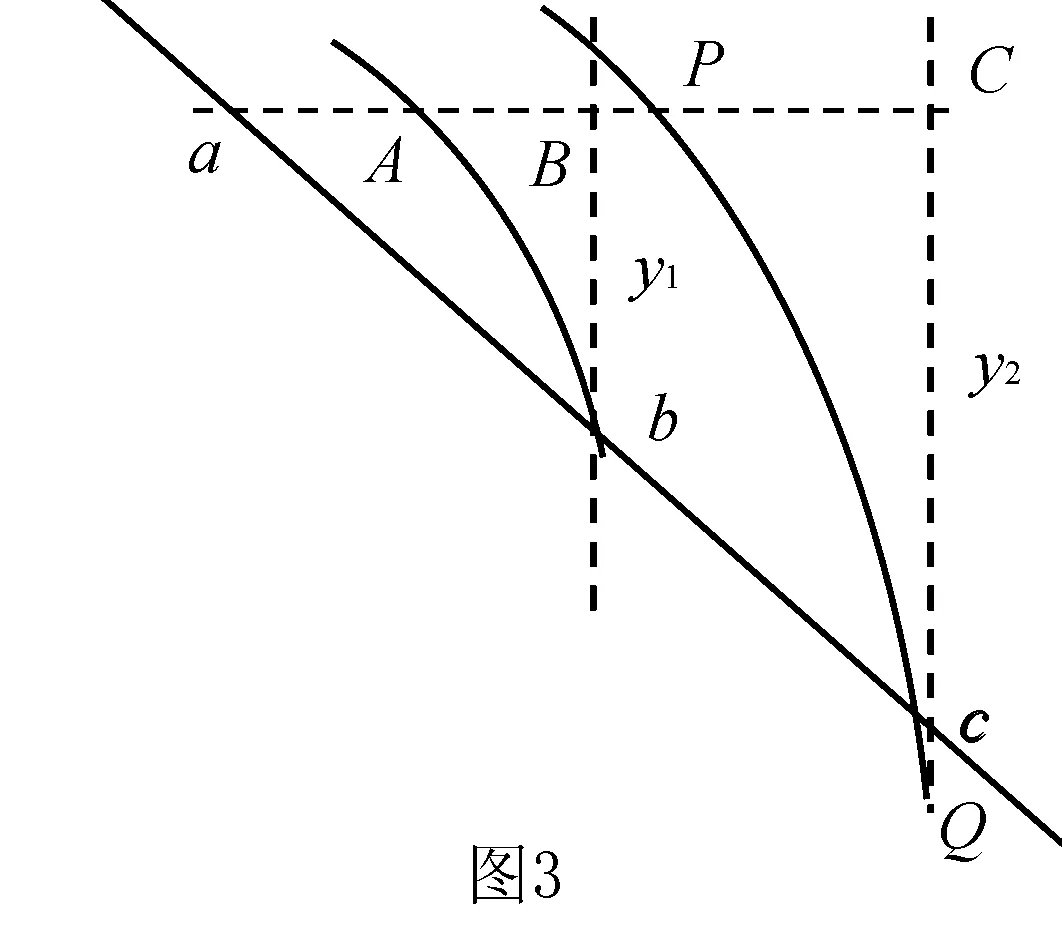
图3
解法1 如图3所示,作过a点的水平线aC与分别过b、c两点的竖直线bB、cC.假设第二颗炸弹的轨迹经过aC线上A点落在斜面上b点,第三颗炸弹的轨迹经过aC线上P点与cC线上Q点.由题意可知,设aA=AP=x0,ab=bc=L,Bb=y1,CQ=y2,斜面的倾角为θ,炸弹到达aC线时的竖直速度均为vy,水平速度均为v0,当第一颗落在a点后,第二、三颗炸弹分别再历时t1、t2到达斜面.由平抛运动规律,可得:
由以上几式可得t2=2t1,y2>2y1;所以Q点应在斜面上c点的下方,也就是第三颗炸弹将落在bc之间,故选项A正确.
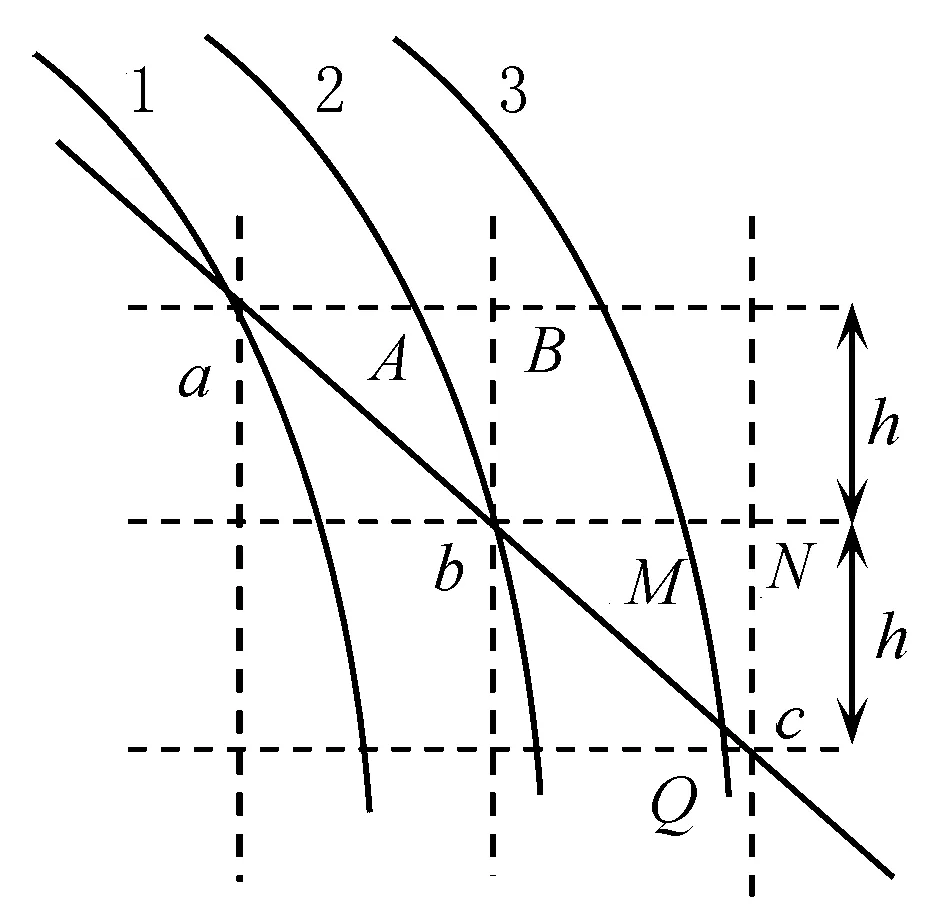
图4
解法2 如图4所示,分别作出过a、b、c三点的水平线与竖直线(图中虚线所示).由题意可知aA=bM,则AB=MN,由于炸弹在竖直方向上做匀加速运动,在竖直方向下落相同高度的时间会越来越短,故炸弹2从A→b的时间大于炸弹3从M→Q的时间,即Ab水平距离大于MQ的水平距离,故Q点应在c点的左侧,炸弹的3轨迹应交斜面于bc之间,选项A正确.
评析平抛运动在水平方向做匀速直线运动,在竖直方向上做自由落体运动.解法1基于定量分析,根据平抛运动在水平方向上做匀速直线运动,因此由水平位移求时间更简便一些.解法2基于定性分析,由于平抛运动在竖直方向做自由落体运动,因此在竖直方向下降相同位移时,所对应的水平位移会越来越小.
解法3 如图5所示,作出炸弹1平抛的轨迹,将此轨迹的镜象平移至位置2、3(注意使1、2与2、3间距相等),它们分别代表三颗炸弹运动的轨迹.在轨迹1上选
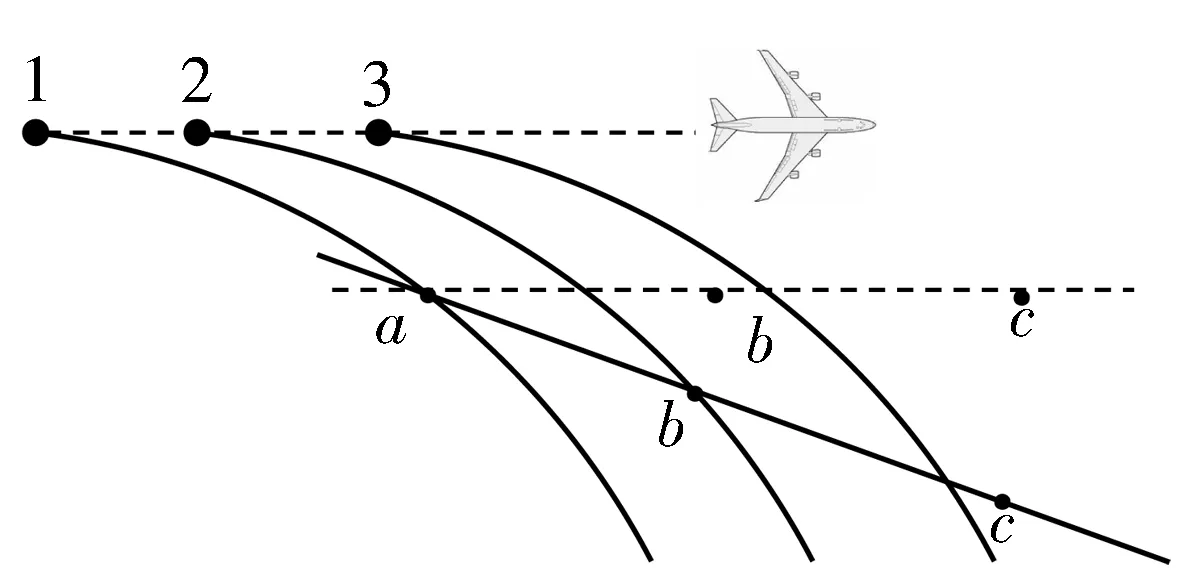
图5
取点a,过a点作水平线(虚线所示),在此水平线上a点右侧依次选取b点与c点,使ab=bc;再将此虚线以a点为转轴,在竖直平面内顺时针旋转,使b点落在轨迹2上(实直线所示),不难看出,此时c点在直线与轨迹3交点的右侧,即表示第三颗炸弹将落在bc之间,故选项A正确.
评析解法3是利用几何作图来求解问题的.几何作图法充分利用了数形结合的思想,把抽象繁杂的物理过程转化为一幅幅具体而清晰的物理图景,将物理问题转化为一个个几何问题,通过几何图形所蕴含的物理意义,从图中寻找答案.这种方法既直观形象,又易于理解,且避免了一些繁杂的推理与计算,对启迪学生思维、拓展学生思路、提高学生学习兴趣有着不可替代的重要作用.
[1]王后雄. 教材完全解读( 高中物理必修2) [M].北京:中国青年出版社,2013(9).

