碰撞规律“瘦身” 提升解题效率
刘桂斌
(广东省佛山市南海区平洲夏东南海区第一中学 528200)
碰撞是高中重点研究的物理模型,包含弹性碰撞、非弹性碰撞和完全非弹性碰撞,由于碰撞作用力大、作用时间短,因此所有碰撞均遵循系统动量守恒,弹性碰撞遵循碰撞前后瞬间动能守恒,非弹性碰撞和完全非弹性碰撞的动能将减小.因此,碰撞模型满足三个规律:
规律1:
系统动量守恒(选取正方向),即m1v1+m2v2=m1v1′+m2v2′
规律2:
系统碰撞前后动能不增加,即
规律3:
碰撞两物体间速度合理,即碰前能相撞,两物体相向运动,或物体同向运动后物速度大于前物速度(v1>v2);碰后不再相撞,两物体速度相反,或碰后同向运动后物速度不大于前物速度(v1'v2')
一、碰撞规律“瘦身”原因
如:质量为m1,速度为v1的物体和质量为m2,同向速度为v2的物体发生弹性碰撞,则碰后m1的速度v1′与m2的速度v2′分别是多少?根据弹性碰撞列出方程组:
m1v1+m2v2=m1v1′+m2v2′
①
②
学生比较难计算出v1′与v2′两个未知数,原因是方程①为一次方程,方程②为二次方程,部分学生将①变形后,采用代入法对方程②进行化简求解,这种解法显然非常耗时,而且少部分学生还做不下去,甚至有数学基础较弱的学生无法求解.因此,很有必要对碰撞规律2进行“瘦身”,避免计算难和费时问题,提高解题效率.
二、碰撞规律如何“瘦身”
运用数学对上面方程组①②进行化简,先对方程②移项后由平方差变形,结合方程①降为一次方程,再和方程①联立求解,具体如下:

移项化简:m1v1+m2v2=m1v1′+m2v2′
平方差展开:m1(v1-v1′)(v1+v1′)=m2(v2′-v2)(v2′+v2)
利用①关系化简:(v1+v1′)=(v2′+v2)
最后可以得到:v1-v2=v2′-v1′
③
③的物理意义可理解为:碰前相对速度大小等于碰后相对速度大小(选取正方向),由化简过程可知,③式已经包含了规律2的碰撞前后动能守恒.
因此,碰撞模型规律可以“瘦身”为满足以下三个规律:
规律1:系统动量守恒(选取正方向),即m1v1+m2v2=m1v1′+m2v2′
规律2:系统碰撞前后相对速度大小不增加(选取正方向),即v1-v2≥v2′-v1′
规律3:碰撞两物体间速度合理,即碰前能相撞,两物体相向运动,或物体同向运动后物速度大于前物速度(v1>v2);碰后不再相撞,两物体速度相反,或碰后同向运动后物速度不大于前物速度(v1'v2').
三个规律都是一次方程,达到了“瘦身”的目的.
三、碰撞规律“瘦身”后的运用
例1 光滑的水平地面有两物体,质量分别为m1=2 kg和m2=1 kg,分别以v1=8 m/s和v2=5 m/s的速度向右运动,追上后发生弹性碰撞,则碰撞后m1和m2速度为多大?如图.
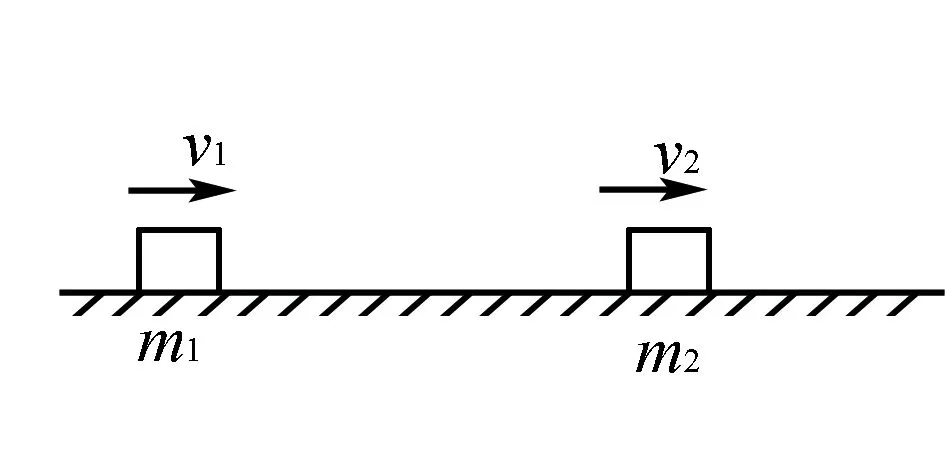
分析两物体发生弹性碰撞,碰后m1的速度v1′,m2的速度v2′,选取向右为正方向,得:
m1v1+m2v2=m1v1′+m2v2′
①
②
而后,直接根据动量守恒和弹性碰撞前后相对速度大小相等,再列出两个一次方程组
m1v1+m2v2=m1v1′+m2v2′
③
v1-v2=v2′-v1′
④
③④代入数据,本题可非常快速计算出:v1′=6 m/s,v2′=9 m/s,效率大大提高.
值得注意的是,由于计算题是根据写出的主干方程给分,方程②要根据动能守恒列出得分方程,以免影响得分.
例2 甲、乙两球在光滑的水平面上,沿同一直线同一方向运动,它们的动量分别为p甲=10kg·m/s,p乙=14kg·m/s,已知甲的速度大于乙的速度,当甲追上乙发生碰撞后,乙球的动量变为20 kg·m/s,则甲、乙两球的质量m甲∶m乙的关系可能是( ).
A.3∶10 B.1∶10 C.1∶4 D.1∶6
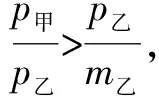
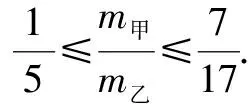
因为判断过程涉及的都是一次方程,因此判断难度降低,解题效率大大提高.
通过将碰撞规律碰撞前后动能不增加这个二次方程,“瘦身”为碰撞前后相对速度大小不增加的一次方程,不仅能够加深对碰撞问题的本质理解,还使得碰撞计算减少了复杂和繁琐的数学化简过程,降低了难度,减少了运算出错的可能性,节约了解题时间,提升了碰撞问题的解题效率.
[1]王广祥.课堂新坐标·高三一轮总复习·物理[M].兰州:甘肃教育出版社,2017:102.

