三道全国卷比较大小试题的分析与启示
张兵源 苏艺伟
(福建省漳州普教室 363000;福建省龙海第一中学新校区 363199)
苏艺伟,从事高考试题,高中数学教学研究.
一、题目
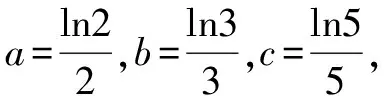
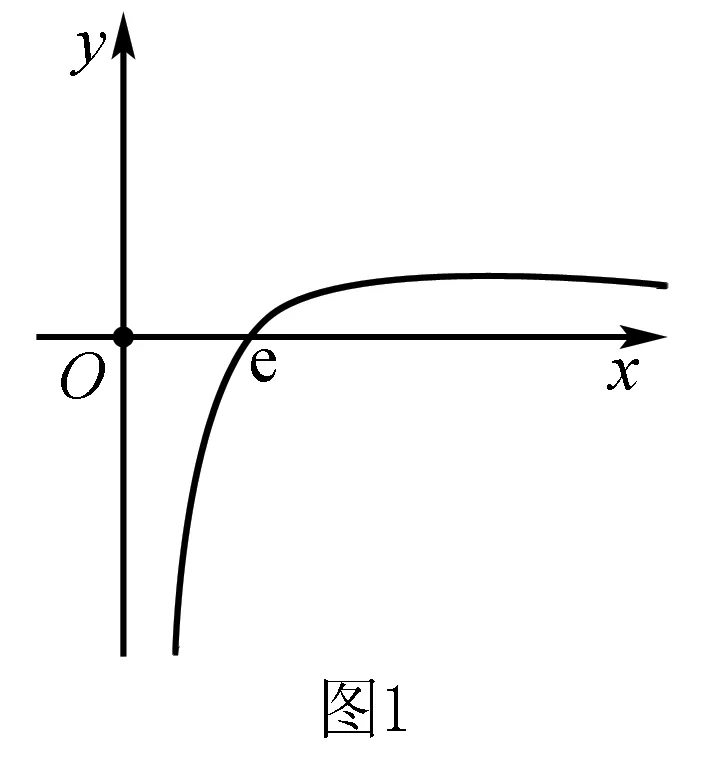
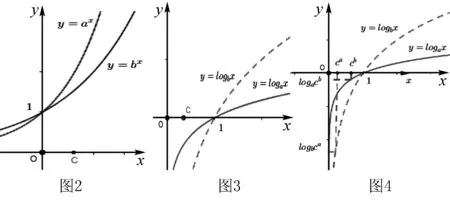
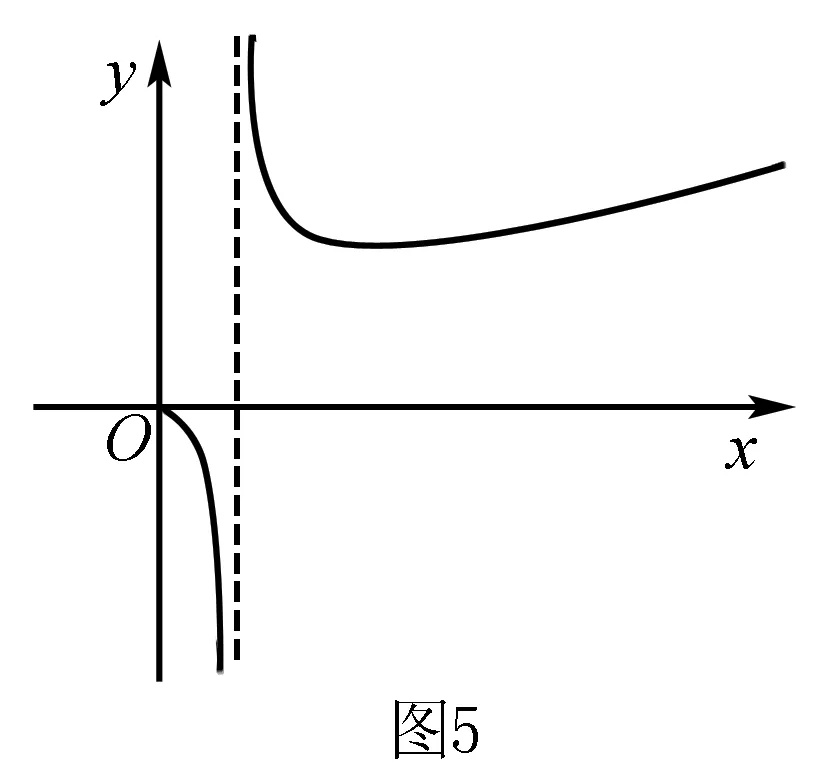
A.a C.c 试题2 (2016年全国Ⅰ卷选择题)若a>b>1,0 A.ac C.alogbc 试题3 (2017年全国Ⅰ卷选择题) 设x,y,z为正数,且2x=3y=5z,则( ). A.2x<3y<5zB.5z<2x<3y C.3y<5z<2xD.3y<2x<5z 这三道比较大小的试题虽然题目不一样,但是考查的内容是一样的.都是考查指数运算与对数运算.要求考生能够借助指数,对数的运算性质,指数函数(或者幂函数),对数函数的单调性,图象,并且综合运用不等式的相关知识进行求解,对考生的计算求解能力,推理论证能力提出了较高的要求.试题虽然简短却内涵丰富,集指数,对数,不等式等众多的知识点于一体,体现了在知识交汇处命题的原则.可以说,这三道试题既考基础又考能力,入口宽,解法多样,具有一定的探究意义. 1.解试题(1) 思路1:作差法 故c 思路2:作商法 由已知有a>0,b>0,c>0. 2.解试题(2) (1)比较ac和bc 对于ac和bc,观察到它们底数不同,指数相同,因而可以采用两种方法来进行比较. 方法1:构造幂函数. 令y=xc,由c>0可知该函数在(0,+∞)单调递增.因为a>b故ac>bc. 方法2:构造两个指数函数. 令y=ax和y=bx,因为a>b>1,故如图(2)所示.由0 综合上述分析可知,ac>bc,故A答案错误. (2)比较logac和logbc 观察到这两个对数式底数不同,真数相同,因此构造两个对数函数进行比较. 令y=logax和y=logbx,因为a>b>1,故如图(3)所示.由0 因此,logbc (3)比较abc和bac 方法1:作差法 abc-bac=ab(bc-1-ac-1),由a>b>1,c-1<0,结合图(2)可知0 故bc-1-ac-1>0,则abc-bac=ab(bc-1-ac-1)>0. 因此abc>bac.故B答案错误. 方法2:综合分析法 因为y=tx在R是单调递增,c<1,故tc 从而B答案错误. 方法3:综合分析法 假设答案正确,则abc 从而B答案错误. (4)比较alogbc和blogac 方法1:利用不等式性质:在不等式两边同时乘以一个正数,不等号不变,同时乘以一个负数,不等号发生改变. 由上述分析知logbc 又由a>b>0,logbc<0得alogbc 综上,alogbc 方法2:利用对数的运算性质:nlogaN=logaNn. alogbc=logbca,blogac=logacb.转化为比较logbca与logacb的大小. 由于0 结合图(4)可知,logbca 3.解试题(3) 思路1:作差法 令2x=3y=5z=k,由于x,y,z为正数,所以k>1. 故2x<5z. 综上,有3y<2x<5z. 思路2:作商法 令2x=3y=5z=k,由于x,y,z为正数,所以k>1. 综上,有3y<2x<5z. 思路3:构造函数法 令2x=3y=5z=k,由于x,y,z为正数,所以k>1. 则有x=log2k,y=log3k,z=log5k, 显然f(x)在(0,1)和(1,e)上单调递减,在(e,+∞)上单调递增.如图(5)所示. 因此有3y<2x<5z. 显然f(x)在(0,e)单调递增,在(e,+∞)上单调递减.如图(1)所示. 令2x=3y=5z=k,由于x,y,z为正数,所以k>1. 则有x=log2k,y=log3k,z=log5k, 因此有3y<2x<5z. 思路5:两边同时取以e为底的对数 由2x=3y=5z得ln2x=ln3y=ln5z,即xln2=yln3=zln5. 综上,有3y<2x<5z. 思路6:取特殊值 令2x=3y=5z=2,则x=1,y=log32,z=log52. 显然3y=3log32=log38 5z=5log52=log532>log525=2=2x, 故有3y<2x<5z. 通过上述分析,不难发现这三道比较大小试题相似程度非常及其之高.这一方面说明全国卷试题的稳定性,在高三备考中要认真钻研历年全国卷试题,并且和自己的教学有机结合起来以期达到最优效果;另一方面说明指数运算和对数运算是高考重点考查的内容(包括指数函数,对数函数,幂函数等的图象与性质),在高三复习中一定要重点讲解,讲透概念,性质,并且进行强化训练以期达到知识能力的迁移;同时,我们还看到全国卷试题的解法多种多样,这就启发我们在课堂上要一题多解,发散思维,并且适当补充相应的方法,技巧,以期让学生内化成自己的能力,提升思维品质和核心数学素养. [1]蔡勇全.善用八种函数的单调性证明不等式[J].高中数学教与学,2017(5):11-14.二、试题分析
三、试题解法
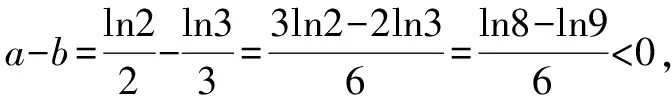
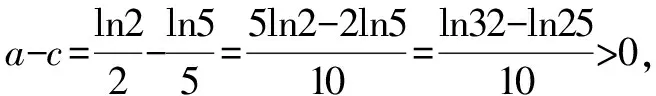
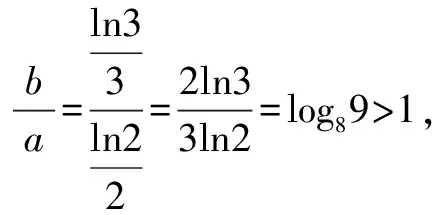
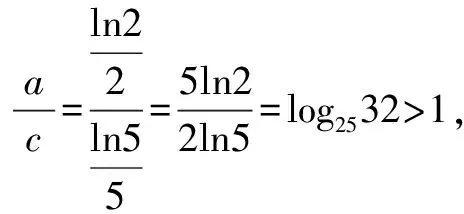
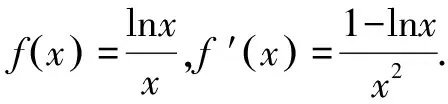
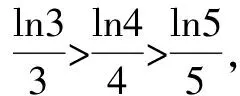
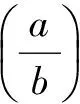
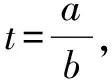
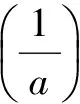
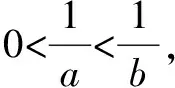
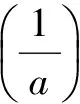
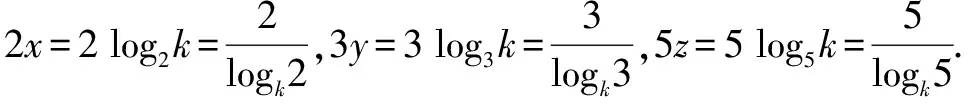
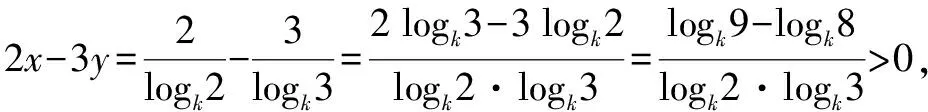
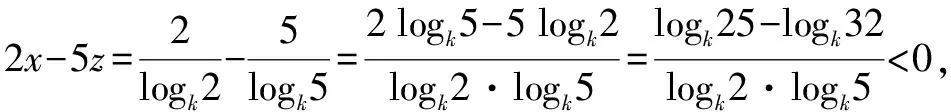
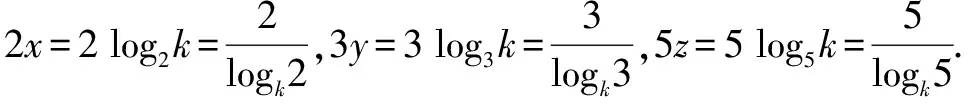
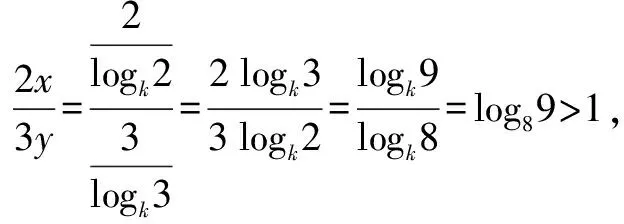
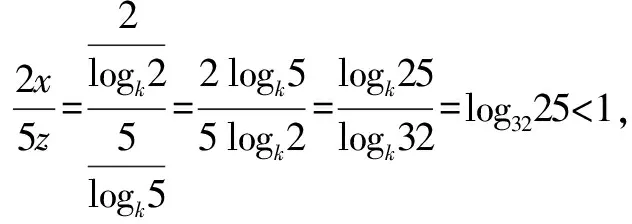
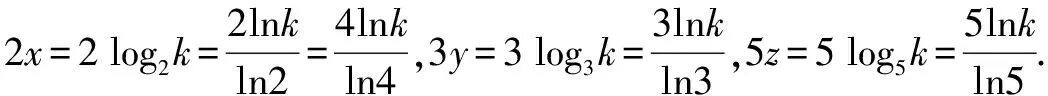
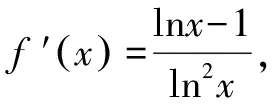
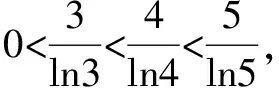
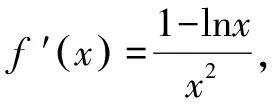
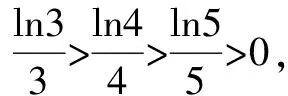
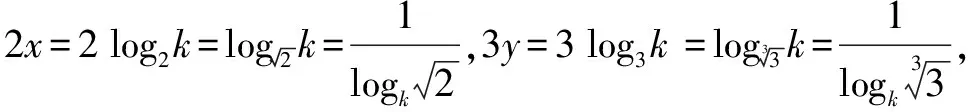
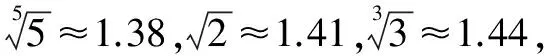
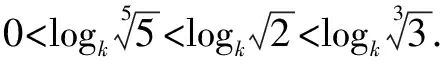
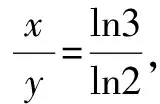
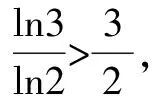
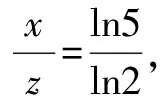
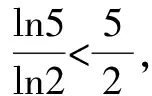
四、教学启示

