利用数位法验算和解决数论问题
刘 畅
(浙江省嵊州中学2016级高二(16)班 312400)
读前须知:
1.本文中用到的引理:
①任意9的倍数m所有数位上的数字之和仍为9的倍数.
②一个正整数减去9的倍数对其各数位上的数字之和无影响.
2.文中为求简便,将用f(x)来表示正整数x各个数位上的数字“彻底相加”后得到的结果.
举例:f(256)=f(13)=1+3=4;
f(2582)=f(17)=1+7=8.
3.以下范例均为解答中验算的一步,非全题.
一、加减法验算中的数位法
例88454+22687=111241是否正确?
解f(88454)=f(29)=2,
f(22687)=f(25)=7,
f(111241)=f(10)=1.
∵f(f(88454)+f(22687))
=9≠f(111241)=1,
∴ 运算错误.
提出结论f(a1+a2+…+an)=f(f(a1)+f(a2)+…+f(an)).
证明结论将a1,a2,…,an都化为n×9+mn的形式,则f(an)=mn,f(a+b)=f(ma+mb)=f(a)+f(b).
同理可得f(a1+a2+a3+…+an)=f(f(a1)+f(a2)+…+f(an)).
拓展也可以用于减法运算的计算,即将其逆向检验.如a-b=c则检验b+c=a是否成立即可,也可以用于复杂的加减运算验算.
二、乘法验算中的数位法
例9876×3456=34131446是否正确?
解f(9876)=f(30)=3,
f(3456)=f(18)=9,
f(34161446)=f(26)=8.
由于f(f(9876)×f(3456))=9≠f(34131446)=8.
∴运算错误.
提出结论f(a1×a2×…×an)=f(f(a1)×f(a2)×…×f(an)).
证明结论同样,将a1,a2,…,an都化为n×9+mn的形式,则
f(a1×a2×…×an)
=f(m1×a2×…×an)
=f(m1×m2×…×an)
=…
=f(m1×m2×…×mn)
=f(f(a1)×f(a2)×…×f(an))
∴f(a1×a2×…×an)=f(f(a1)×f(a2)×…×f(an)).
拓展同样,也可以用于减法运算的验算中,只需将得出的答案乘以除数验算即可.
三、实际运用
数位法可以方便地用于选择题与填空题中,但是不能出现在解答题的解题过程中.但在不写出解答过程的情况下不失为一种很好的简化计算的方法.
例1 求方程1335+1105+845+275=n5的整数解.
注这是浙江省数学会2017夏令营代数部分的一道例题,官方的方法较为复杂,但经过数位法可以较为简便地得出解.
解显然n≥134.
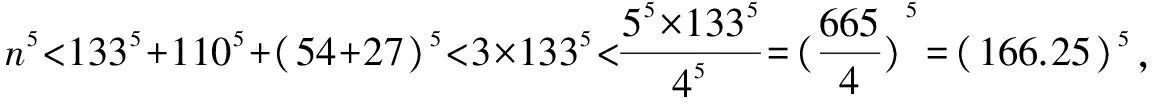
∴134 引理:n5与n的个位数相等, ∴n的个位数为4, ∴n只能为134,144,154,164其中一个. 由数位法得f(1335+1105+845+275)=f(4+5+9+9)=9, ∴f(f(n5)=f(1335+1105+845+275)=9. 要f(n5)=9,则f(n)必为3的倍数,即n为3的倍数, ∴n为144. 例2 22225555+55552222≡____(mod 3). 引理1.若一个数n被3整除,则f(n)≡0(mod 3); 若余x,则f(n)≡x(mod 3). 2.若一个数n被9整除,则f(n)≡0(mod 9); 若余x,则f(n)≡x(mod 9). 3.f(nx)=f(f(na)b) 其中a×b=x. 解∵f(2222)=8,f(5555)=2, ∴f(22225555)=f(85555),f(55552222)=f(22222), f(85)=1,f(26)=1. ∵f(85555)=f(811115)=f(81111)=f(8222×8)=f(87)=8, f(22222)=f(26370×22)=f(2372)=1, ∴f(22225555+55552222)=9, 即22225555+55552222≡0(mod 3) 评析此题是一道综合性比较强的例题,需要有较好的运算能力.运用数位法可以较为快速地解出答案. 在做幂比较大的运算时,要善于寻找特殊值,使得幂可以依次减小,从而优化运算. 例3 求满足方程2x×3+2=2u×5v,x≥2的正整数解(x,u,v). 注本题改编自全国高中数学联赛模拟卷第二试中的数论例题,利用数位法可以完成其中一部分运算. 解当x≥2时,显然u=1,于是得到2x-1·3y+1=5v. 当y=1时,得到2x-1·3+1=5v. ∵2x的末位为数列2,4,8,6,2,4,… ∴3·2x的末位为数列6,2,4,8,6,2,… ∴x=4k+4,k∈N. ∵易知f(24k+3·3)=6, f(5v)为数列5,7,8,4,2,1,5…, ∴v=6m+2,m∈N. ∴原方程转化为24k+3×3+1=56m+2, 显然k=m=0是解. ∴矛盾. ∴只有k=m=0满足条件, 即所求整数解为(4,1,1,2). 最终,我们得出这样一个通用结论: f(a1+a2+a3+…+an) =f(f(a1)+f(a2)+…+f(an)). f(a1×a2×a3×…×an) =f(f(a1)×f(a2)×…×f(an)). 在实际运用中,先计算每一个数的f(x)值,再进行验算比较简便. 数位法运算比较适合现在的各个年龄段学生使用,从小学高年级的四则运算,到全国高中数学联赛的数论,数位法都有可能发挥作用.尤其是在使用计算器频率较高的情况下,中学生的运算准确率的确很让人担忧.而利用这种方法,可以很快发现笔算中不易找到的错误. 我相信,如果能够在实际运用中使用数位法进行验算,不仅计算的正确率能够大大提升(尤其是对于一些较为复杂的计算),而且还可以简化运算,省下时间攻破更难的题目. [1]李潜.全国高中数学联赛模拟试题精选[Z].合肥:中国科学技术大学出版社,2017. [2]曹瑞彬.启东中学奥赛精题详解高中数学[Z].南京:南京师范大学出版社,2016(02).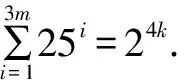

四、结论

