采用调零天线阵测向解GNSS姿态仪的整周模糊度
石荣,刘畅,张伟
(电子信息控制重点实验室,四川 成都 610036)
0 引 言
在利用全球四大卫星导航系统GPS,GLONASS,BD,GALILEO来完成定位、授时和测速服务之外,还可以实现载体的姿态测量[1-2],即完成载体的航向、俯仰、横滚等参数的估计,从而为各类飞机、舰艇等提供定姿数据,该方法相对于惯导系统来讲,具有成本低、精度比较恒定、不会产生累积误差等优点[3]。从20世纪90年代起,世界上各大公司就开始了基于GPS的测姿系统研制与试验工作[4]。Trimble公司早期的TANS VECTOR机载测姿系统试验就已经表明:当采用1 m基线时姿态测量精度为0.331°;5 m基线时姿态测量精度可达到0.06°[5].虽然GNSS姿态测量具有一系列优点,但在使用过程中存在需求快速求解测向方程中的整周模糊度问题。近十几年来工业界与学术界开展了大量的研究工作,也提出了各种办法,例如:双频伪距法、模糊度函数法、模糊度协方差法、基于LAMBDA的模糊度值搜索算法、基于载波相位双差的优化模糊度函数法等[3,5,6],但这些方法在工程应用中也存在解模糊耗时长、所要求的应用条件高的问题;而其它的一些方法,要求系统必须工作于多频状态[7],或者需要通过多模组合来达到解模糊的目的[8],使其不能在单频工作的单模GNSS姿态仪中有效应用。
实际上整周模糊度解算问题在电子侦察的干涉仪测向中也同样存在,在该应用中是通过多基线干涉仪中的短基线来解长基线的相位差模糊[9-11]。参照上述应用,采用GNSS调零天线阵所自然形成的二维测向短基线,用此短基线去实时解算GNSS姿态仪中的长基线在对导航卫星来波方向测向过程中的相位差模糊。这样一来,在实际应用中同一个平台上既安装GNSS姿态仪,又安装GNSS调零天线,二者的组合应用不仅能够提高GNSS姿态仪定位测姿的性能,而且还能增强整个卫星导航系统抗干扰反欺骗的能力[12],这也极大地增强了军用卫星导航系统在现代战争中的鲁棒性和顽存性。
1 GNSS姿态测量中的整周模糊度问题
1.1 GNSS姿态测量原理简述
载体坐标系中YC轴与载体运动方向的中心线重合,XC轴垂直于YC轴指向载体右侧,ZC轴与XC、YC轴成右手坐标系。而本地东北天坐标系中,东对应XL轴,北对应YL轴,天对应ZL轴。
联系人: 石荣E-mail: Email:wyx1719@sina.com
在载体平台完成自身定位后,即可计算出在本地东北天坐标系中,由载体指向第i颗导航卫星的方向性单位矢量αi=(αX,i,αY,i,αZ,i)T;i∈{1,2,…,M},M为当前可视的导航卫星的数目。另一方面,载体平台通过姿态仪的测向天线阵对第i颗导航卫星信号的来波方向进行测向,从而得到在载体坐标系中载体指向该卫星的方向性单位矢量βi.上述两个在不同坐标系中描述同一方向的单位矢量之间有如下关系式成立:
βi=MYMXMZαi,
(1)
式中,MY,MX,MZ分别为由载体姿态参数决定的空间三维旋转矩阵
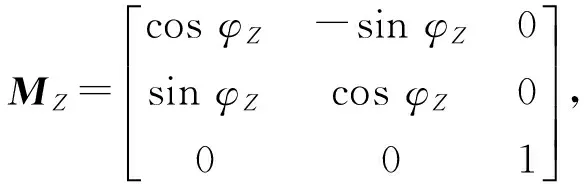
(2)
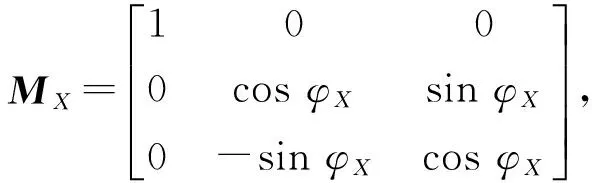
(3)
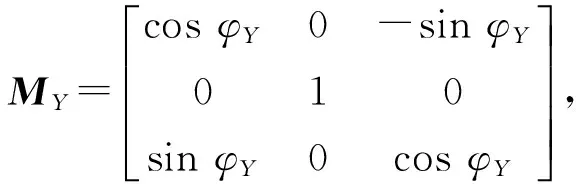
(4)
式中:φZ,φX,φY分别表示载体平台的航向角、俯仰角和横滚角,这也就是待求的姿态参数。由上述可知,从理论上讲只要M≥3,即只需要对3颗导航卫星的来波方向实施二维测向,即可建立3个独立的方程,从而求解出平台的姿态参数。但根据GNSS定位原理,在M≥4时才能确保完成平台的自身定位,所以对于GNSS姿态仪来讲,也需要满足此条件。此时能够建立超过3个的独立方程来求解3个姿态参数,所以采用如下的最小二乘法能求解出更加精确的结果。
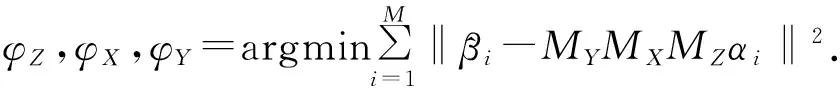
(5)
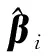
1.2 长基线测向中存在的整周模糊度问题
前述姿态解算过程需要在载体坐标系中对各颗导航卫星的来波方向进行测量,这通常是通过载体上GNSS姿态仪所正交布置的AB、CD两条长基线两端的导航天线通过相位差分处理实现的,如图1所示。
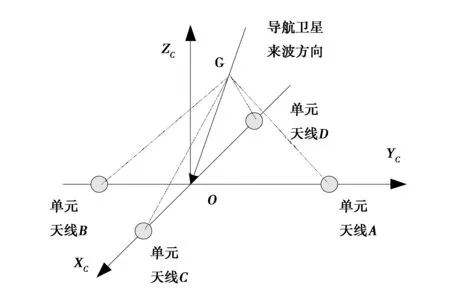
图1 载体上的长基线测姿天线单元
以图1中导航卫星信号来波方向GO与基线AB所构成的二维平面为例,通过相位差测量来推算来波方向如图2所示。
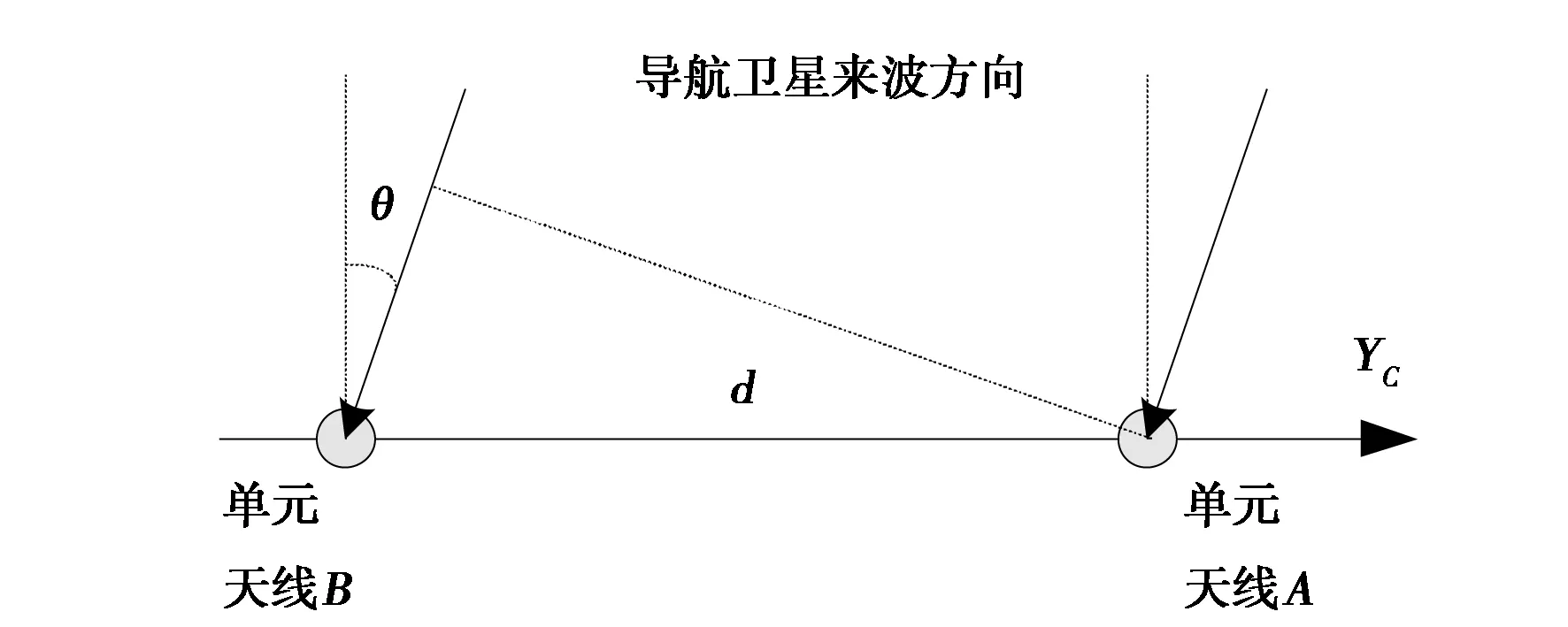
图2 通过单元天线之间的相位差推算来波方向
设图2中卫星导航信号来波方向与AB基线的法线方向之间的夹角为θ,基线AB的长度为d,那么单元天线A、B之间的相位差φ满足下式:
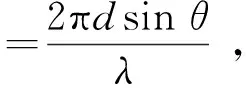
(6)
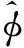
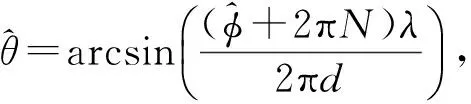
(7)
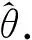
2 多基线干涉仪测向及解模糊
实际上类似于图2中通过单元天线之间的相位差测量来估计信号来波方向的应用在电子侦察中是非常普遍的,在电子侦察领域通常称之为干涉仪测向。在干涉仪测向中同样面临着基线过长时相位差模糊问题,而解决方法通常采用长短基线配合的多基线干涉仪,通过短基线的相位差测量值去解长基线相位差测量值的模糊。图3为长短基线组合的干涉仪测向图。
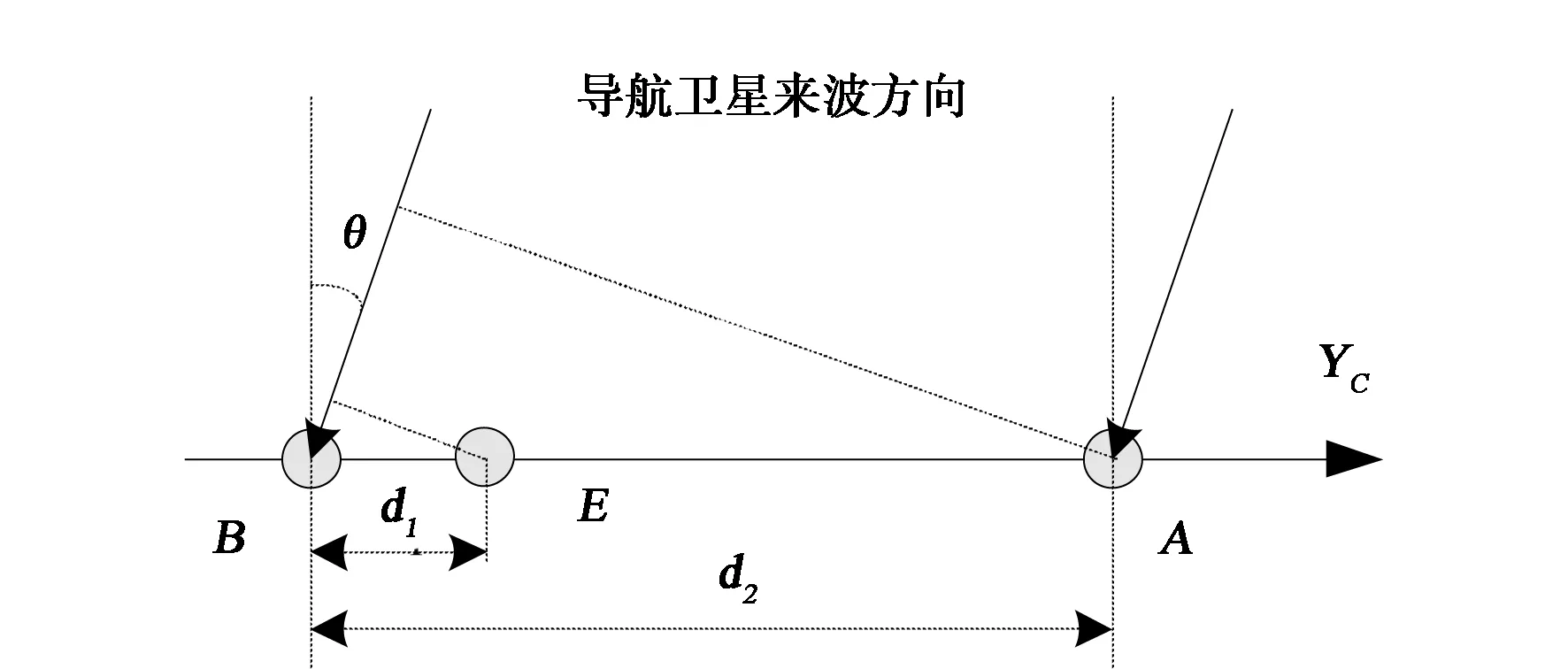
图3 通过长短基线组合的干涉仪测向
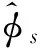
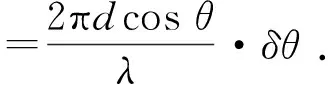
(8)
由式(8)可知,在相位差测量误差δφ保持一定的条件下,基线越长,测向误差δθ越小。考虑到相位差的取值范围φ∈[-π,π)。所以只要长基线d2与短基线d1之间满足式(9),即可用短基线的相位差测量值去解长基线的相位差模糊。
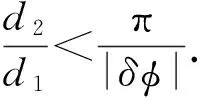
(9)
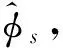
(10)
同理,在三基线干涉仪测向中,用最短基线的相位差测量值去解中等长度基线的相位差的整周模糊度,然后再用中等长度基线的相位差去解长基线的相位差的整周模糊度。以此类推,在多基线干涉仪测向中,通过不同长度基线之间的逐级解模糊来获得最终的最长基线的精确相位差测量值。最后再由式(7)计算出导航信号的准确来波方向。
由上可见,上述模糊度解算过程是完全实时实现的,只要长短基线同时对同一个信号的相位差进行测量,便可立即得到无模糊解。所以在电子侦察中通常把多基线干涉仪用于单脉冲测向,即使该脉冲信号的持续时间仅有1 μs,多基线干涉仪仍然可以瞬时获得该脉冲信号的准确来波方法。这对于战场环境下的应用具有特别重要的意义,因为外界人为的故意电磁干扰会使得GNSS姿态仪频繁发生信号的失锁与再捕获,其有效接收信号的时间非常短,采用多基线测向解模糊才能确保在极短的时间内获得导航卫星的准确来波方向测量值,从而为后续的平台姿态解算提供有效的输入。所以该方法相比于其它方法来讲,其抗干扰性能更强。
3 利用调零天线充当短基线
通常情况下,考虑到姿态测量中的精度要求和工程实现性,GNSS姿态仪的基线长度一般在5 m左右。如果对天线单元之间导航信号相位差的测量精度控制在3°以内。则由式(9)可知,即使长基线长度为5 m,则下一级短基线的长度为8.3 cm,而GPS的L1信号(1 575.42 MHz)的波长约为19 cm,那么8.3 cm的短基线小于半波长。由此可见,可以通过2条长短基线的设计来完成多基线相位差测量的解模糊。那么如何构建更短的测向基线呢?
一方面可以在两条长基线的基础上,分别增加2个天线单元E,F,由此来构成短基线BE和DF,如图4所示。由短基线BE的相位差测量值去解长基线AB的相位差整周模糊度;由短基线DF的相位差测量值去解长基线CD的相位差整周模糊度。
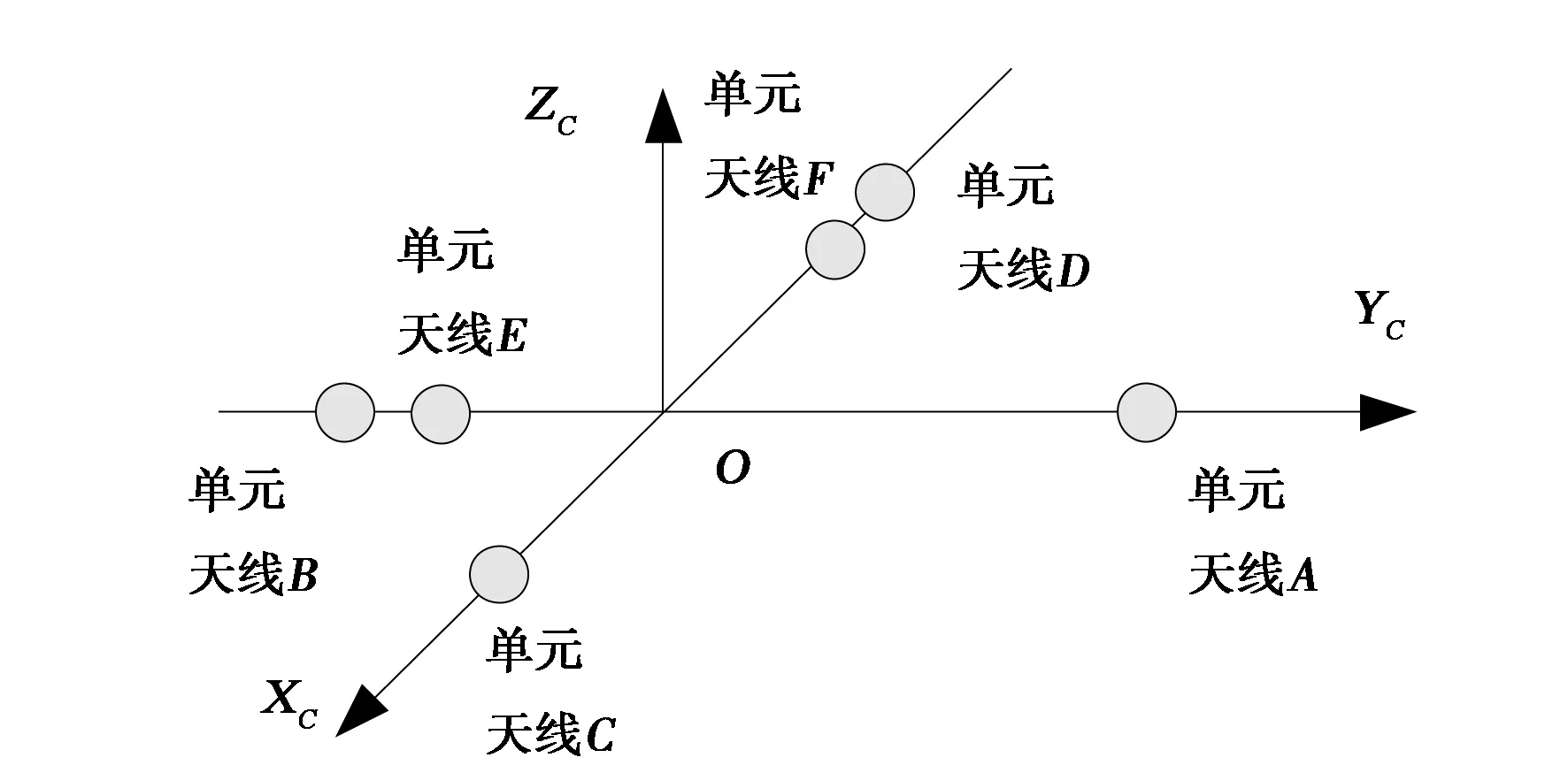
图4 通过新增单元天线来构建短基线
但如图4所示的设计方案需要更改GNSS姿态仪的硬件。如果要保持现有GNSS姿态仪硬件不变,而只需对软件进行修改完善,那么新增加的测向短基线需要另外的接收天线阵来提供,此时自然想到调零天线阵。卫星导航调零天线阵原本是用来抵抗压制干扰,即通过多单元天线接收信号的加权求和在干扰信号来波方向上形成天线波束方向图零点。实际上调零天线阵也是一个多天线多通道接收系统,而且各个相邻单元天线之间的间距通常小于半波长。借用调零天线阵所自然构成的短基线,利用多基线干涉仪测向原理,即可用短基线的相位差测量值来解长基线所形成的相位差模糊。
在所选取的调零天线阵具有相互垂直的2条短基线的条件下,将此调零天线安装于平台上时,特地使2条相互垂直的短基线与GNSS姿态仪中相互垂直的2条长基线的方向保持平行,这样就可以直接用短基线的相位差测量值去解GNSS长基线相位差测量的整周模糊度。以矩形布阵的4元调零天线阵为例,调零天线阵与GNSS姿态仪天线在载体上的布置如图5所示。
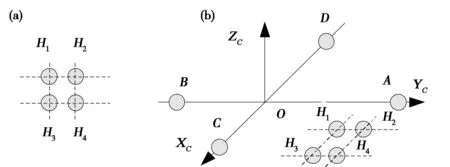
图5 调零天线阵与GNSS姿态仪天线的布置图示(a)四元调零天线; (b)载体上的单元天线布置
在图5(a)的四元调零天线阵中,基线H1H2、H3H4与基线H1H3、H2H4垂直,将此调零天线与GNSS姿态仪安装于同一载体上如图5(b)所示,调零天线的基线H1H2、H3H4与GNSS姿态仪的基线AB保持平行,调零天线的基线H1H3、H2H4与GNSS姿态仪的基线CD保持平行。如此布置,即可用短基线H1H2、H3H4的相位差测量值去解长基线AB的整周模糊度;同样用短基线H1H3、H2H4的相位差测量值去解长基线CD的整周模糊度。
如果所选取的调零天线阵没有相互垂直的2条短基线,此时在将调零天线阵安装于载体上时,至少可以使得天线阵的1条基线与GNSS中的1条基线保持平行;而另一条长基线的解模糊可通过与之相交夹角最小的短基线来完成。只不过由于两条基线没有完全平行,所以解模糊的角度区间需要通过投影映射来确定。
4 仿真验证
以2017年9月15日下午4点30分在成都地区执行飞行任务的一架同时安装有GPS姿态仪与GPS调零天线阵的飞机为例进行分析。该飞机此时正在做圆周转向飞行,姿态数据真值分别为:航向角128.6°,俯仰角6.2°,横滚角8.3°.该飞机在完成自身定位之后给出的定位数据为:东经104.695°,北纬32.718°,高度2400 m.由此可计算出在本地东北天坐标系中,可见的各颗GPS卫星信号的来波方向的方位角与俯仰角,以及来波方向在本地东北天坐标系中对应的单位矢量αi如表1所示。表中PRN表示各颗GPS卫星的伪码号。
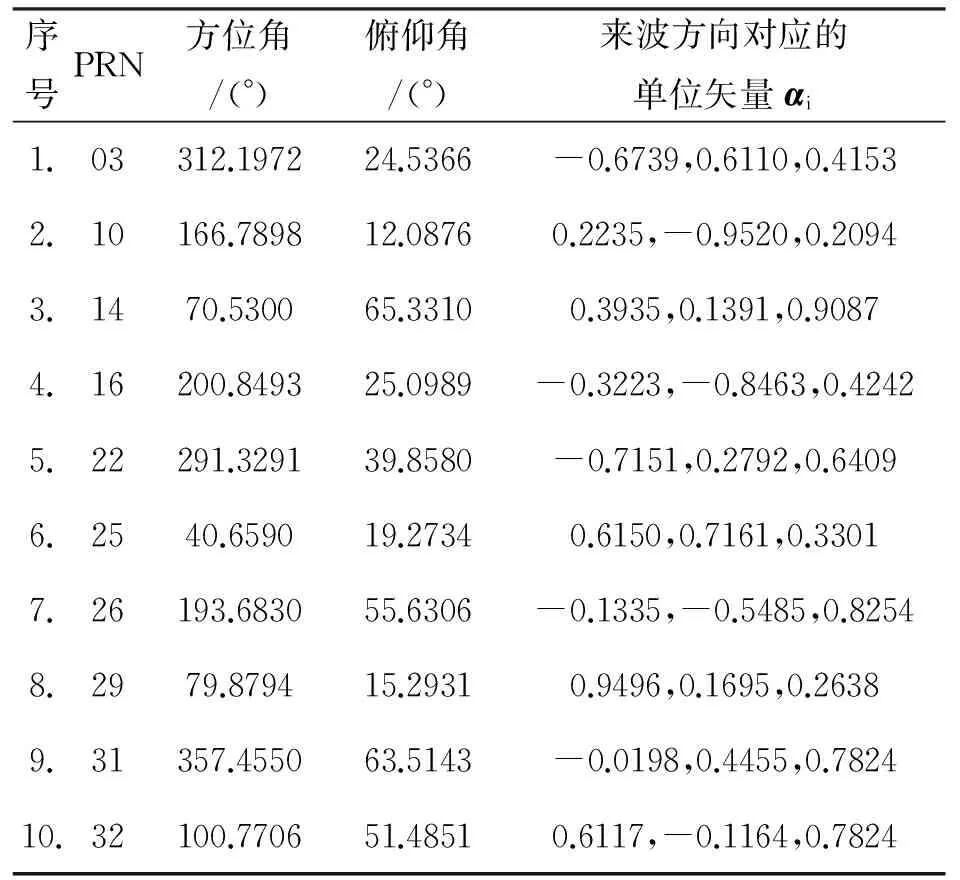
表1 各颗GPS卫星的来波方向角
飞机上安装的四阵元调零天线与GPS姿态仪如图5(b)所示。其中姿态仪中两条相互垂直的基线AB=CD=5 m,调零天线中两条相互垂直的基线H1H2=H1H3=0.09 m.以姿态仪的2条基线与调零天线的2条基线为参考,进行单元天线之间接收不同GPS卫星信号的相位差测量,所得到的数据如表2所示,其中相位差测量误差在3°(对应0.052 4 rad)以内。
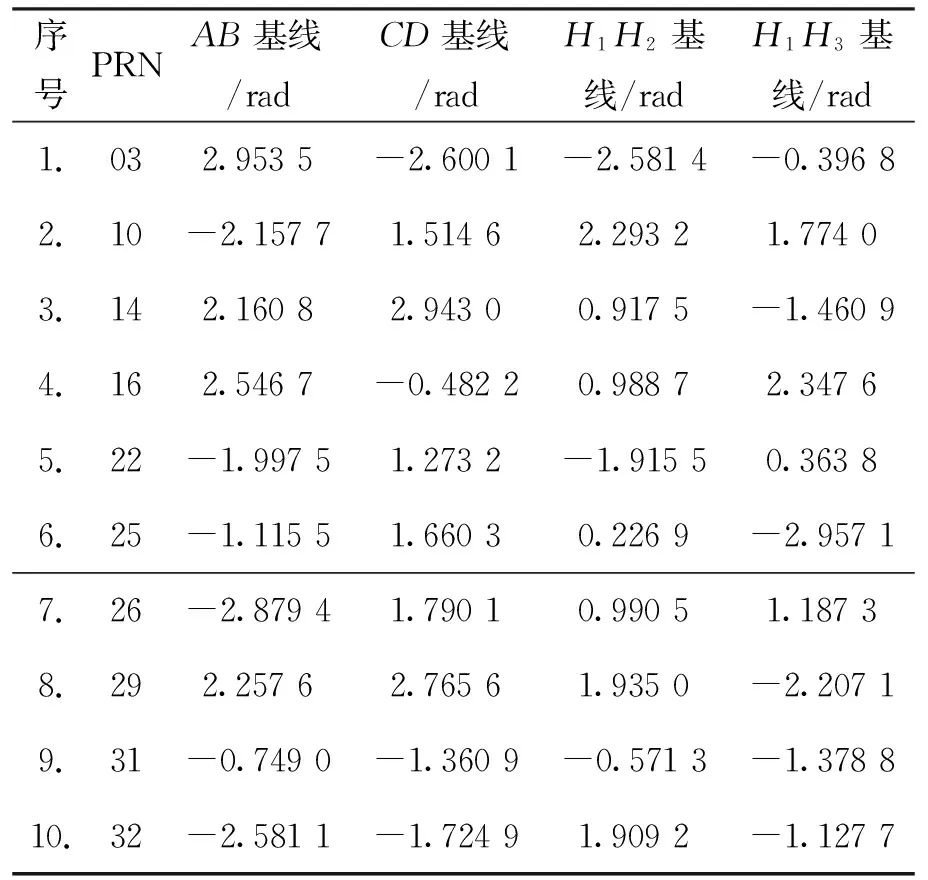
表2 GPS姿态仪与调零天线测量得到的相位差
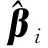
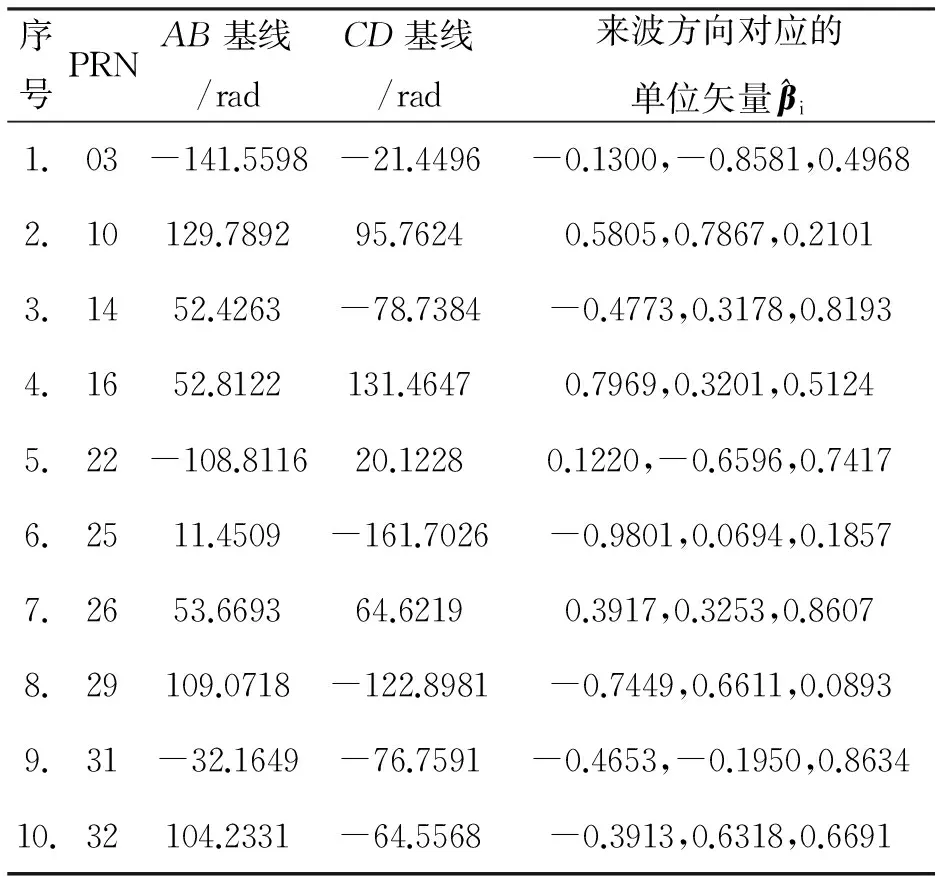
表3 解模糊后的相位差及各颗GPS卫星来波方向角
根据式(5),采用最小二乘法可求解得到该飞机此时的姿态参数分别为:航向角128.59°,俯仰角6.18°,横滚角8.27°.上述测量值与真值之间的误差分别为:-0.01°,-0.02°,-0.03°.由此可见,利用调零天线阵提供的短基线可以实现GPS姿态仪的相位差模糊的实时快速解算。
5 结束语
采用卫星导航调零天线阵自身所具有的二维短基线这一天然条件,通过短基线的相位差测量值来实时解算GNSS姿态仪中二维长基线相位差测量值的整周模糊度,从而实现了平台姿态的快速解算。该方法将卫星导航调零天线与GNSS姿态仪结合在一起进行应用,不需要对二者的硬件架构进行修改,仅需要增加部分处理软件即可投入工程应用;另一方面,二者的结合使用不仅提升了整个卫星导航系统定位测姿的性能,而且也提升了其抗干扰反欺骗的性能。仿真试验结果验证了上述方法的可行性与有效性,从而为GNSS姿态仪和调零天线的拓展应用提供了重要参考。
[1] TEUNISSEN P, OMONTENBRUCK O. Handbook of global navigation satellite systems[M]. Germany: springer, 2017.
[2] KAPLAN E D, HEGARTY C J. Understanding GPS principles and applications [M].2ed. USA: MA, Norwood, ARTECH HOUSE, INC. 2006.
[3] 吴美平,胡小平,逯亮清. 卫星定向技术[M].2版. 北京:国防工业出版社,2013.
[4] 许江宁,朱涛,卞鸿巍. GPS姿态测量技术综述[J]. 海军工程大学学报,2003,15(3):17-22,36.
[5] 韩慧群. GPS姿态测量系统研究与开发[D]. 哈尔滨:哈尔滨工程大学,2006.
[6] 刘若普. GPS三维姿态测量技术[D]. 上海:上海交通大学,2008.
[7] 王建敏,马天明,祝会忠. BDS/GPS整周模糊度实时快速解算[J]. 中国矿业大学学报,2017,46(3):672-678.
[8] 宋玉龙,廉保旺,唐成凯. 基于多频模糊度解算的BDS/GPS中基线AEKF RTK算法[J]. 系统工程与电子技术,2017,39(8):1794-1800.
[9] RICHARD A. Poisel. Electronic warfare target location methods [M]. 2ed.USA: Artech House Inc. 2012.
[10]MATINO A D. Introduction to modern EW systems [M]. USA: Artech House Inc. 2012.
[11]POISEL R A. Electronic warfare receivers and receiving systems [M]. USA: Artech House Inc., 2014.
[12]石荣,徐剑韬,阎剑. 利用调零天线测向与夹角比对的导航欺骗信号检测[J]. 现代导航,2017,8(3):193-198.

