自适应调零天线对抗技术仿真研究

白雪妨

(中国电子科技集团公司第二十九研究所,四川 成都 610036)

0 引 言

自适应调零天线能有效地从空域上反电子对抗,利用不同的自适应算法,灵活改变各天线单元的相位和幅度加权(复加权,即W1,Wi,Wn),以此来控制天线方向图的方向和形状。以输出信号y(t)功率降低至最小为准,调节对每个辐射单元的加权值(即W1,Wi,Wn),生成对着干扰的方向图零陷点。当干扰越强的时候,零陷就越深,从而抑制干扰[1]。自适应调零天线原理示意图如图1所示。

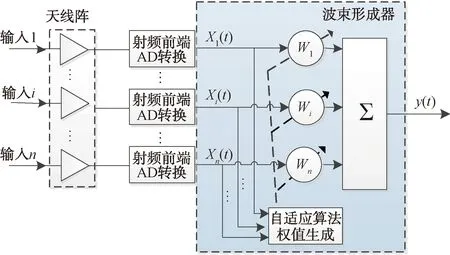
图1 自适应调零天线原理示意图

自适应调零天线在雷达、通信等领域应用广泛,其对抗效能评估是电子对抗研究的重点和难点[2]。

基于自适应调零天线原理,所有的自适应调零天线在数学上都可以当作是一个逐渐趋于最优化的过程。但是这个寻求最优化的过程不可避免地会带来很多负面的影响,比如信号处理算法难度增加、信号处理时间延长、系统的硬件设施增多、电子系统通联时间延长以及电子系统利用率下降等问题。

为了有效地对抗自适应调零天线系统,结合上述自适应调零天线的特点,本文采用了分布式闪烁交变干扰策略来进行研究。

1 对抗策略、方法与干扰样式设计

通常情况下,闪烁干扰与交变干扰要结合使用。

分布式闪烁干扰是干扰自适应调零天线系统的有效途径之一[3]。在有干扰的前提下,天线系统从截获到信号,到进行处理运算,形成自适应调零天线方向图零陷点需要一定的时间,假如干扰信号时断时续或者干扰信号的入射方向来回切换,则必然会导致系统难以确定干扰信号的特征,无法对其进行干扰。

而交变干扰技术可以影响自适应算法性能的发挥,借助于最佳交变技术的研究与应用,可以使自适应算法基本上失效。

自适应调零天线技术的重点是加权系数(即W1,Wi,Wn)的最优化设计,而常用的加权系数设计算法(自适应算法)有最小均方准则、最小方差准则、最小平方准则、最大检测概率准则和最大输出信噪比准则等[4]。以上5种算法各有相应的优势,但又有局限性。

以交变干扰样式研究作为切入点,改变干扰信号的脉冲描述字(PDW),即输出频率、输出幅度、相位、脉宽以及调制样式等性能[5],使系统不断地处于调整和适应的状态之中,以至于难以正常工作,进而使得上述自适应算法性能降低直至失效。

2 自适应调零天线对抗的数字仿真试验数据与结果分析

在分布式闪烁交变干扰与自适应调零天线的对抗试验中,正常信号的来波方向为(0.0°,0.0°),选取2个干扰源,而2个干扰都在3 dB主波束以外,但在主波束以内。

干扰来波方向如图2中波束图中的叠加指示。采用在正常波束方向图基础上叠加一个方向性指示来表示干扰的来波方向。

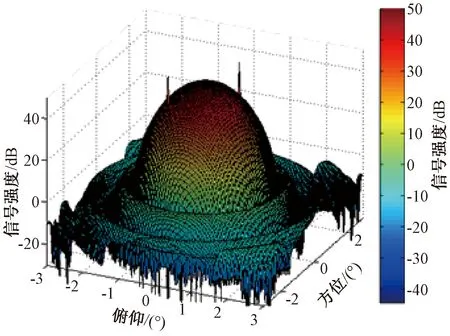
图2 干扰来波方向图示

为了进行对比,将常规干扰样式(包括全频段噪声阻塞干扰、部分频段噪声阻塞干扰、全频段梳状谱阻塞干扰、部分频段梳状谱阻塞干扰)的干扰效果与设计的分布式闪烁交变干扰样式进行对比试验。

2.1 采用“全频段噪声阻塞干扰”

对2个干扰源进行调零后的天线波束方向图如图3所示。可见自适应调零收敛速度在20 ms之内。2个干扰来波方向上形成了2个零陷,且零点宽度在0.2°以内。在第1个干扰来波方向上,对应的调零深度为47.56 dB;在第2个干扰来波方向上,对应的调零深度为67.88 dB。

图3 对干扰来波调零之后的波束方向图示

在全频段噪声阻塞干扰样式下,自适应调零误差随时间变化如图4所示。

由于天线3 dB主波束的宽度为1°,实际上干扰来波方向是位于3 dB主波束以外的,所以天线主波束的增益几乎没有太大的变化,调零之后主波束增益如图5所示。

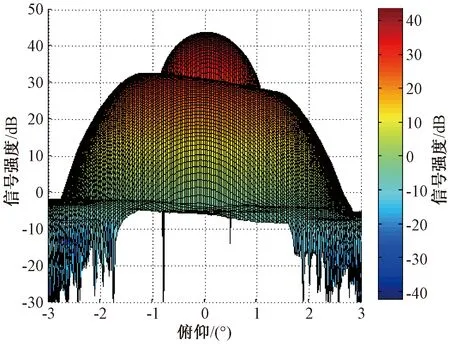
图5 自适应调零之后的主波束增益图

2.2 采用“部分频段噪声阻塞干扰”

对2个干扰源进行调零后的天线波束方向图如图6所示。

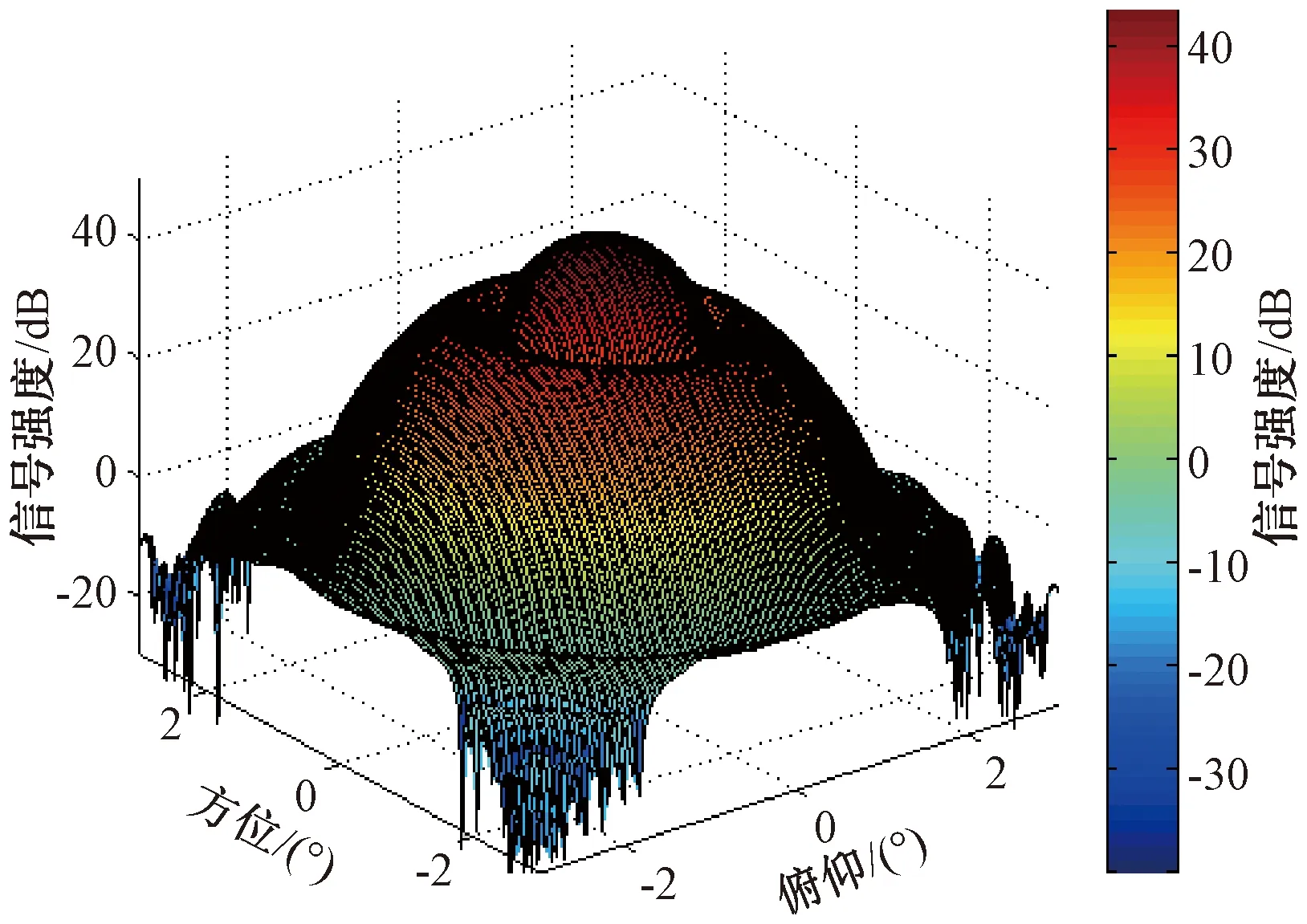
图6 对干扰来波调零之后的波束方向图示

在部分频段噪声阻塞干扰样式下,自适应调零误差随时间变化如图7所示。

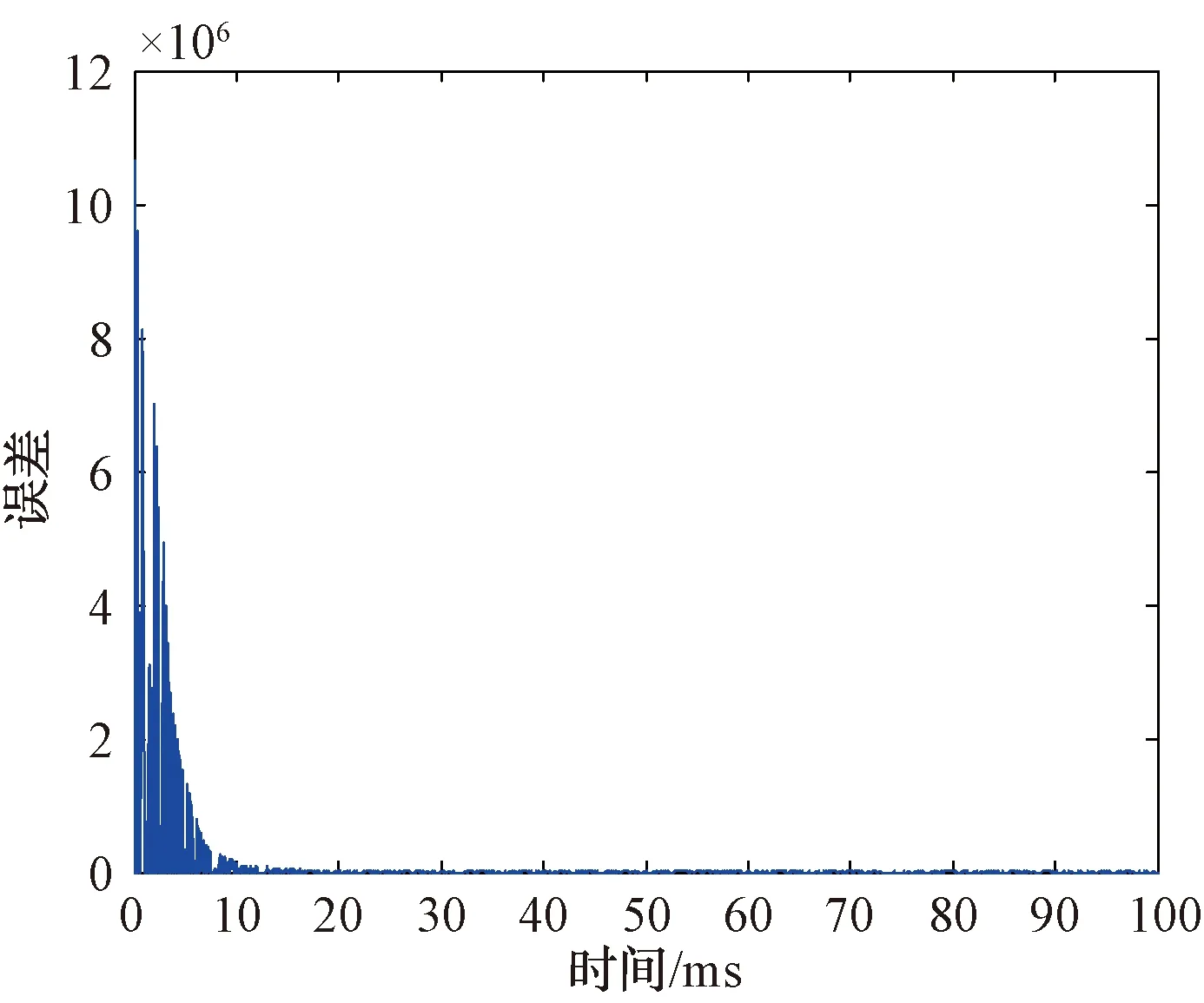
图7 自适应调零误差时间变化的曲线图

可见,自适应调零收敛速度在20 ms之内。2个干扰来波方向上形成了2个零陷,且零点宽度在0.2°以内。在第1个干扰来波方向上,对应的调零深度为45.08 dB;在第2个干扰来波方向上,对应的调零深度为52.15 dB。

由于天线3 dB主波束的宽度为1°,实际上干扰来波方向是位于3 dB主波束以外的,所以天线主波束的增益几乎没有太大的变化,调零之后主波束增益如图8所示。

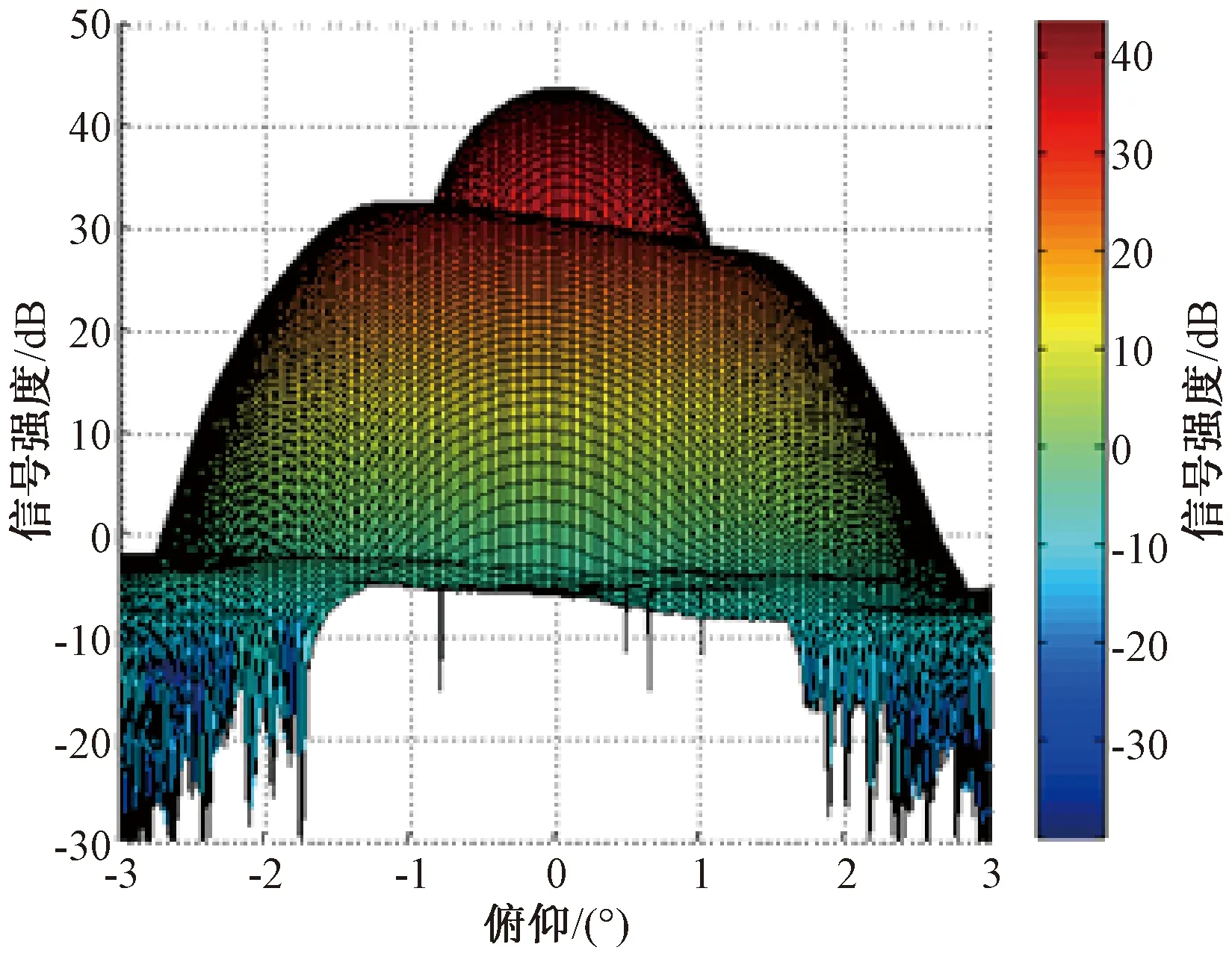
图8 自适应调零之后的主波束增益图

2.3 采用“全频段梳状谱阻塞干扰”

对2个干扰源进行调零后的天线波束方向图如图9所示。

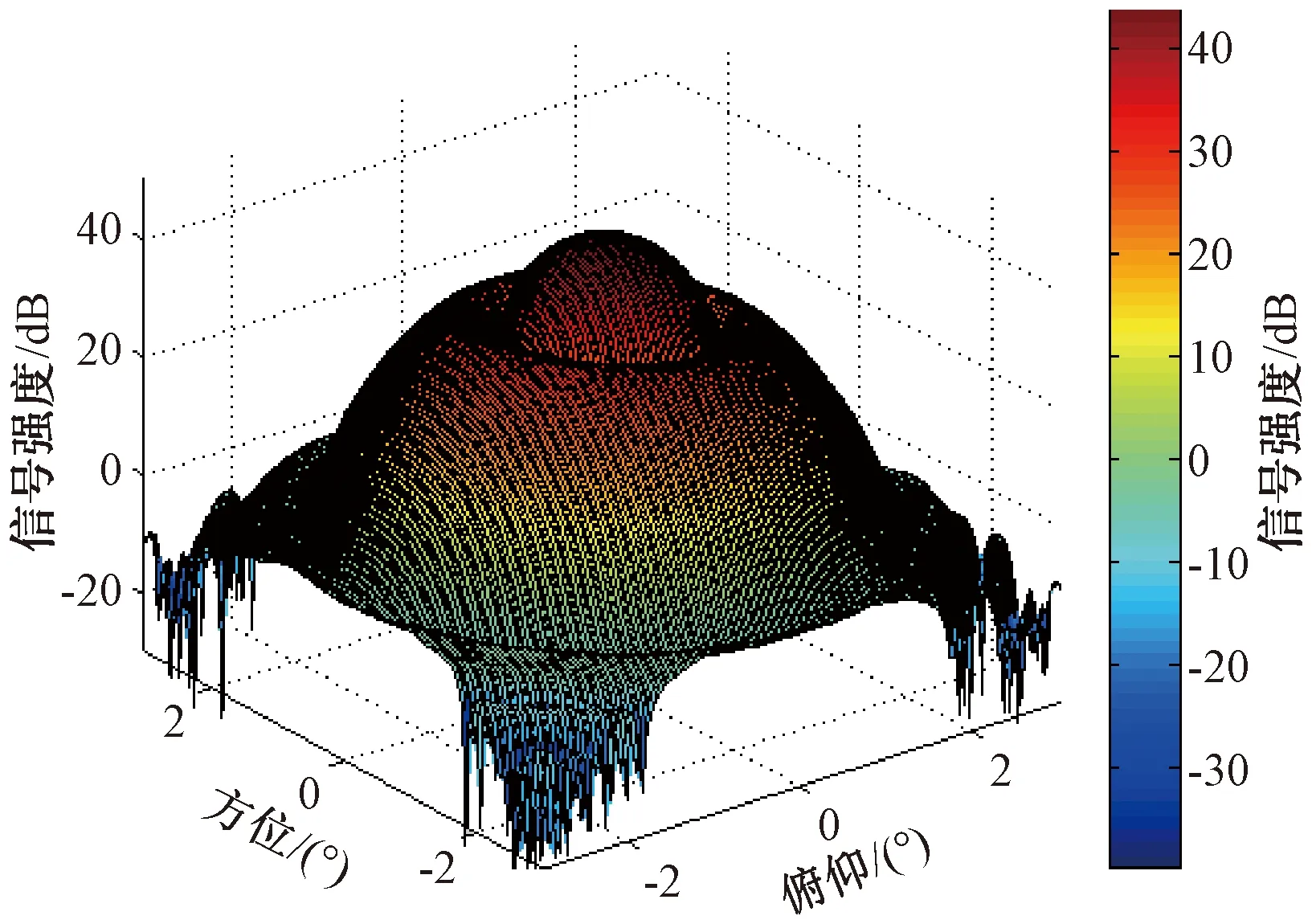
图9 对干扰来波调零之后的波束方向图示

在全频段梳状谱阻塞干扰样式下,自适应调零误差随时间变化如图10所示。

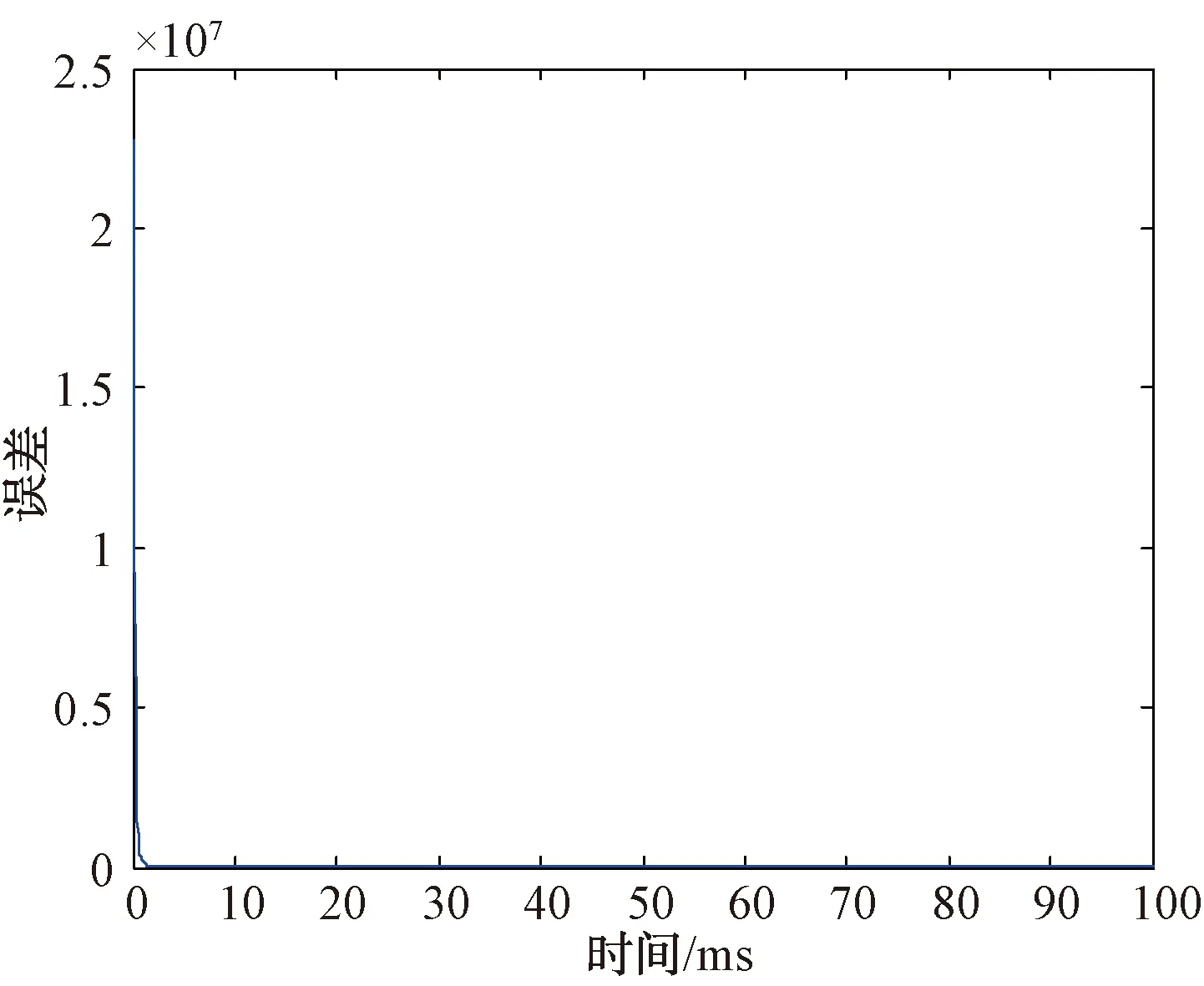
图10 自适应调零误差时间变化的曲线图

可见,自适应调零收敛速度在20 ms之内。2个干扰来波方向上形成了2个零陷,且零点宽度在0.2°以内。在第1个干扰来波方向上,对应的调零深度为50.96 dB;在第2个干扰来波方向上,对应的调零深度为52.32 dB。

由于天线3 dB主波束的宽度为1°,实际上干扰来波方向是位于3 dB主波束以外的,所以天线主波束的增益几乎没有太大的变化,调零之后主波束增益如图11所示。

2.4 采用“部分频段梳状谱阻塞干扰”

对2个干扰源进行调零后的天线波束方向图如图12所示。

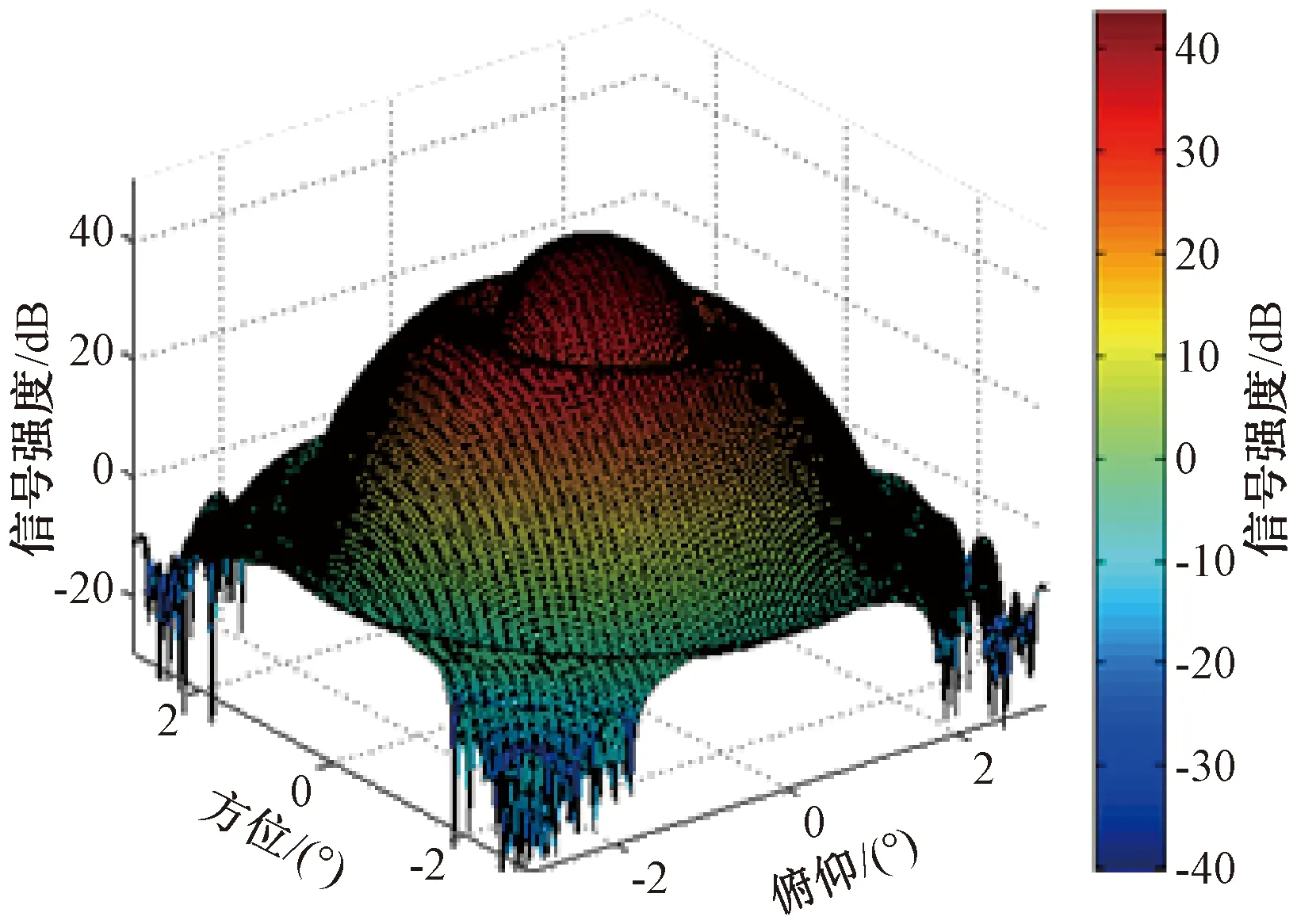
图12 对干扰来波调零之后的波束方向图示

在部分频段梳状谱阻塞干扰样式下,自适应调零误差随时间变化如图13所示。

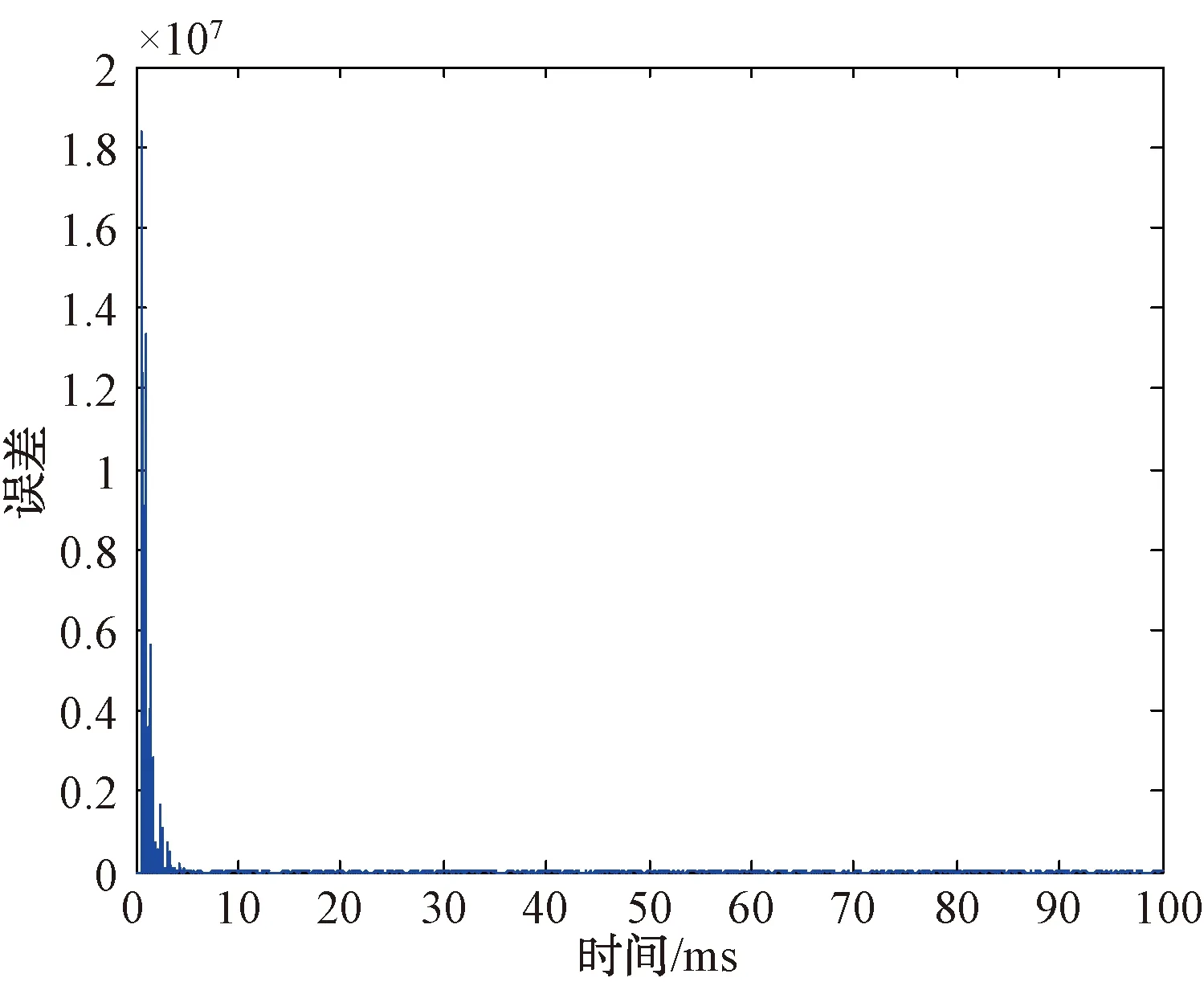
图13 自适应调零误差时间变化的曲线图

可见,自适应调零收敛速度在15 ms之内。2个干扰来波方向上形成了2个零陷,且零点宽度在0.2°以内。在第1个干扰来波方向上,对应的调零深度为47.66 dB;在第2个干扰来波方向上,对应的调零深度为51.70 dB。

由于天线3 dB主波束的宽度为1°,实际上干扰来波方向是位于3 dB主波束以外的,所以天线主波束的增益几乎没有太大的变化,调零之后主波束增益如图14所示。

图14 自适应调零之后的主波束增益图

2.5 采用“分布式闪烁交变干扰”

对2个干扰源进行调零后的天线波束方向图如图15所示。

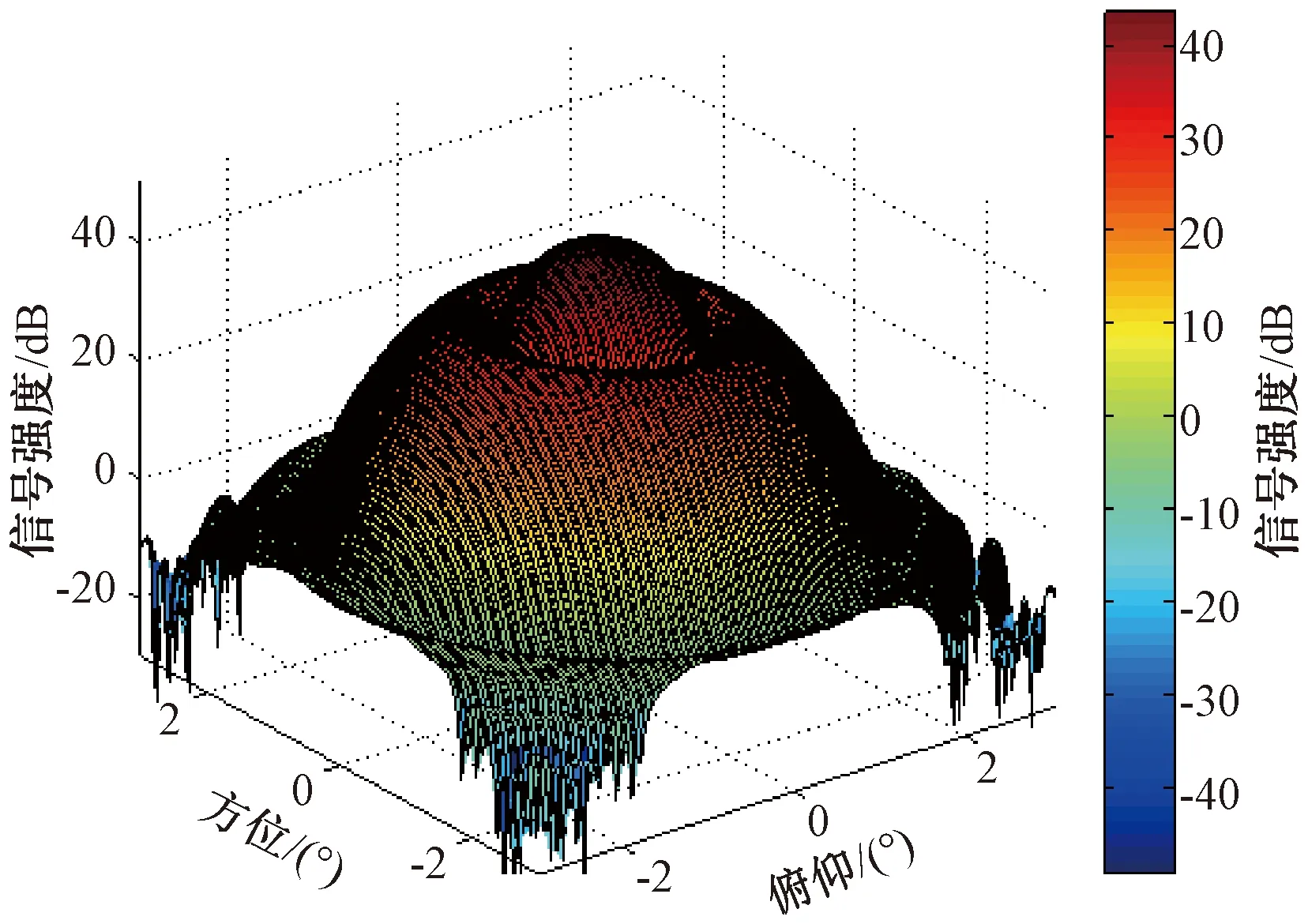
图15 对干扰来波调零之后的波束方向图示

在分布式闪烁交变干扰样式下,自适应调零误差随时间变化如图16所示。

图16 自适应调零误差时间变化的曲线图

由图16可见,自适应调零收敛速度在8 ms之内。在2个干扰来波方向上进行调零。在第1个干扰来波方向上,对应的调零深度为 5.44 dB;在第2个干扰来波方向上,对应的调零深度为14.73 dB。

由于天线3 dB主波束的宽度为1°,实际上干扰来波方向是位于3 dB主波束以外的,所以天线主波束的增益几乎没有太大的变化,调零之后主波束增益如图17所示。

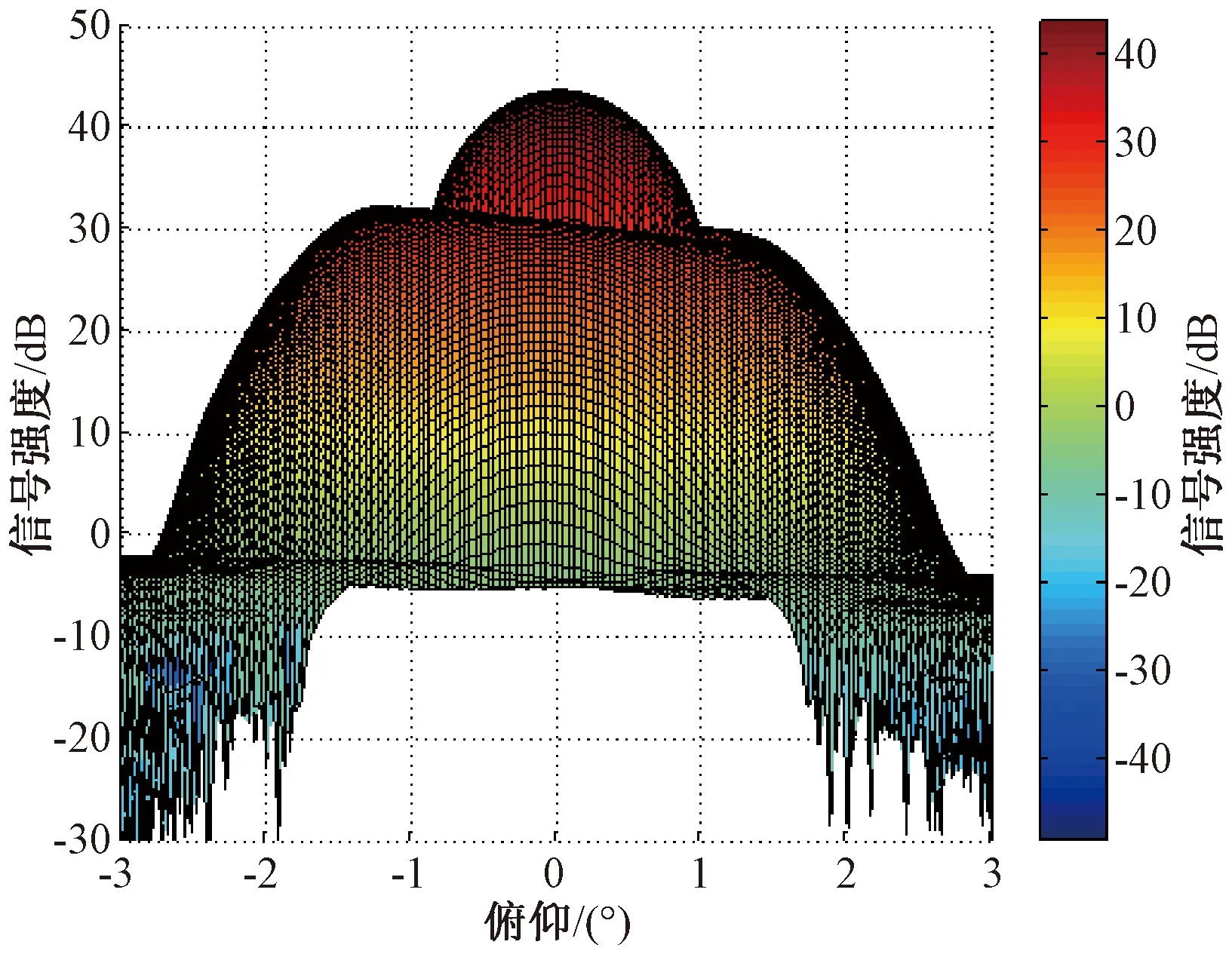
图17 自适应调零之后的主波束增益图

2.6 干扰效果分析

将自适应调零天线对上述5种干扰样式调零的效果总结对比如表1所示。

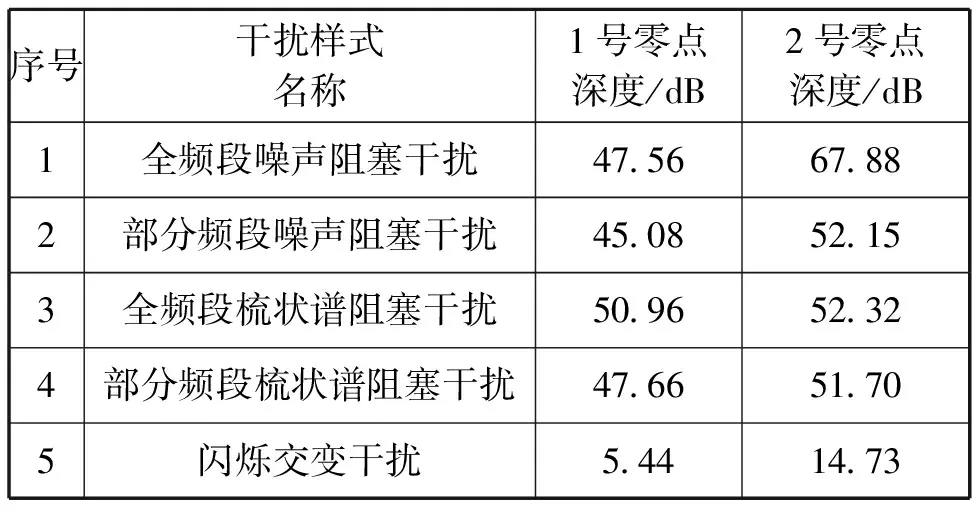
表1 干扰样式的干扰效果对比列表

由上述试验数据的对比可知,采用分布式闪烁交变干扰样式,可以使自适应调零天线的零陷能力降低30 dB以上,可以有效对抗自适应调零天线。

3 结束语

本文主要针对自适应调零天线对抗技术进行研究,从自适应调零天线的对象分析、薄弱环节分析、对抗方法、干扰样式等方面进行了分析与论述。

本文开展了对抗数学仿真试验,从仿真试验结果看,所研究的干扰样式可以实现对自适应调零天线的有效干扰。