巧用学生“错误”唤醒课堂生命力的源泉

路国跃

摘 要：错误就是通向成功的阶梯，学生犯错的过程应看作是一种尝试的过程。由于学生的认知方式与思维策略不同，学生经常会出错。而“错误”又是学生认知水平最真实的反映，蕴含着宝贵的“亮点”。教师若能巧用学生错误，让错误顺化学生的知识结构，便能使自身知识体系更加完善，就能再次唤醒课堂的生命力。

关键词：错误；宽容；探索能力

在教学过程中，出错是不可避免的。教师要善于捕捉错误，把错误当作难得的生成资源加以利用，那么课堂就会碰撞出智慧的火花。笔者结合自己的教学工作，总结出经常会遇到的问题，并针对这些“错误”给出自己的做法。

一、心容错误，了解学情

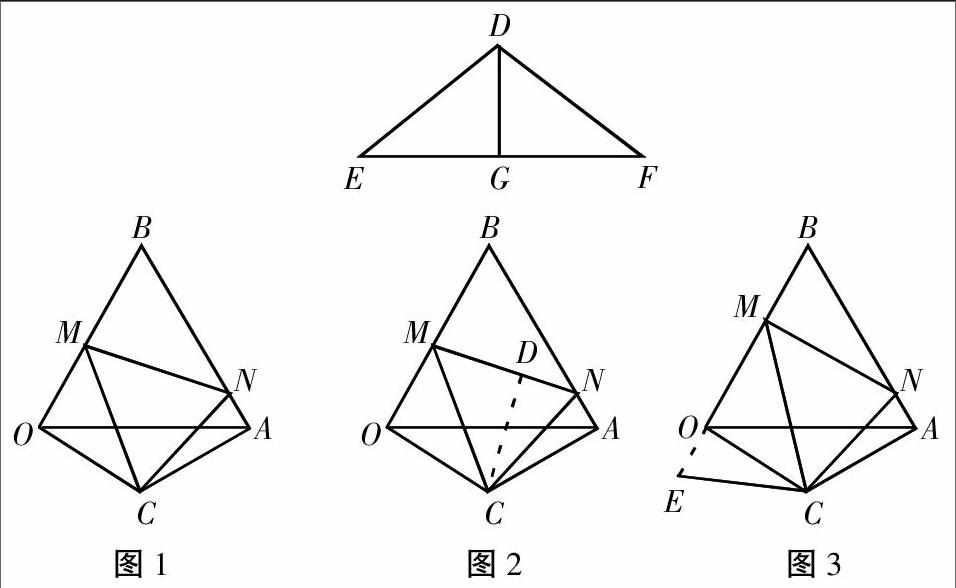
案例1.在学完勾股定理的逆定理以后，笔者出示如下题目：“如图，已知△DEF中，DE=17cm，EF=30cm，EF边上的中线DG=8cm，试判断△DEF是否为等腰三角形，并说明理由。”

思考片刻后，学生开始书写过程。在巡视过程中，笔者发现学生有共性问题。过程如下：“因为DG是中线，所以EG=FG=4cm，又因为DQ2+EG2=289，DE2=289，即DQ2+EG2=DE2，所以DG⊥EF，又因为DG是EF中线，所以DF=DE=17cm”于是笔者用投影展示了该题。

学生1：在Rt△DGE中，通过勾股定理的逆定理推出DG⊥EF，又因为DG是EF中线，根据“三线合一”性质，所以DF=DE=17cm

学生2：根据DG垂直平分EF，也可以得到DF=DE=17。

学生3：还可以通过△DGE≌△DGF，得到DF=DE=17。（笔者：方法不错，尤其是垂直平分线的性质，那么对学生1的方法有质疑吗？此时，笔者将学生1的过程投影出来，片刻后……）

此案例中，笔者发现学生1的错法后并没有立即呵斥，而是继续察看其他学生的情况。原因有二：一是通过察看，发现类似错误很多，把握学情后，为接下来的点评做准备；二是如果立即纠正学生1的错误，就会引起其他学生的注意，不利于他们继续暴露自己的错误。学生只有把自己的思维完全呈现后再纠正，他们的领悟才能更深刻。

二、活用错误，培养探索能力

案例2.在全等三角形的复习课上，笔者出示以下题目：“如图1，等边△OAB，另一等腰△OCA与△OAB有公共边OA，OC=AC，∠C=120°，现有∠MCN=60°，其两边分别与OB、AB交于点M、N，连接MN，将∠MCN绕着点C旋转，使M、N始终在边OB和边AB上。试判断△BMN的周长是否发生变化？并说明理由。”

学生1：将△OMC沿MC折叠，得到△DMC，如图2，再证明△DNC≌△DNA，得DN=AN，所以MN=OM+AN，所以△BMN的周长为MB+MN+BN=MB+OM+AN+BN=OB+AB=6。（下面的学生频频点头，表示赞同。这时，笔者并没有点评正确与否，而是引导学生思考“将△OMC沿MC折叠，得到△DMC”，点D能否落在MN上）

学生2：若MC平分∠OMN，点D就能落在MN上，但M、N在运动，MC不一定平分∠OMN。（笔者：你的思维很严谨）

学生3：可在MN上截取MD=MO，再证DN=AN。（笔者：好像能行，同学们好好研究，看看行不行。经过一番讨论，无法证明全等，学生都否决了这一方法）

学生4：好像可以，将△NAC绕点A逆时针旋转120°，就能等到图3中的△EOC，这样就可以不用证明△EOC≌△NAC，直接得EC=AC，∠ECO=∠NCA，再证△MEC≌△MNC，从而得到MN=OM+AN。（这时，下面学生一片哗然，啧啧称奇。笔者及时点赞，并问旋转后可证明△MEC≌△MNC，那就是说OE与OM共线？能证明吗？从推理角度看，是否需要证明？学生表示需要，并一一给予证明）

此案例中，学生解题一波三折，通过发现—验证—再发现，最终功夫不负有心人。教师面对学生的初次失败时不要心急，要循序渐进，通过师生对话、生生对话找出问题，再探索。

“错误中往往孕育着比正确更丰富的发现和创造因素，发现的方法就是试错的方法。”所以在教学中，教师要广积学生的错误，并给予适时指导和帮助，从而有效帮助学生纠正错误、提升能力。心理学家盖耶认为：“谁不考虑尝试错误，不允许学生犯错误，就将错过最富成效的学习时刻。”

参考文献：

[1]陶晓花.善待小学数学课堂中的错误[J].二十一世纪教育思想文献，2007（1）.

[2]陈世祥.数学教学中学生错误资源的有效利用[J].理科考试研究（初中版），2011.