基于DOB的炮管RBF神经网络滑模控制研究
陈宇政,高 强,侯远龙,瞿生鹏,胡继辉
(南京理工大学 机械工程学院,江苏 南京 210094)
作战坦克炮管是一种长形的负载机构。在坦克炮执行调炮任务时,炮管需准确快速响应控制指令,在一定时间内到达发射角度并保持稳定。而由于炮管自身结构的特点,会使整个调炮过程中产生不平衡力矩,严重影响调炮精度及作战能力[1]。因此,平衡与消除火炮身管定位与身管运动过程中产生的非平衡力则显得尤为重要。由于炮管在平衡过程中存在着诸多非线性因素,若采用传统的控制策略则难以取得理想的控制效果。而滑模控制能充分利用被控目标模型特征,根据实际情况迫使系统处于“滑模”运动状态,并且可以不受外界干扰和系统参数改变的影响。但由于滑模控制本身固有的抖振问题,阻碍了滑模控制的发展与应用,学者们对此问题进行了深度的研究与交流,并提出了一系列基于滑模控制的复合控制方法[2-3]。
文献[4]在传统的滑模控制基础上融入了RBF神经网络调参策略,并把它用于解决高超声速飞行器存在的高度非线性及强耦合的问题,通过仿真可知,该方案不仅能使飞行器拥有响应快速性,抗干扰稳定性和鲁棒性,而且还克服了飞行机构的抖振问题。文献[5]把RBF神经网络滑模控制理论应用于解决多自由度并联机床系统存在的非线性控制问题,仿真试验证明,该控制器能有效克服外界干扰,保证系统鲁棒性的同时也为RBF神经网络理论的应用提供了充分的实验基础。
综上可知,在滑模控制中融入RBF神经网络智能控制算法,对消除抖振有很大的效用[6-9]。因此笔者针对坦克炮身管精准定位与平衡的问题提出了一种基于RBF神经网络的滑模控制策略(RBF-SMC)。为了使该控制策略的抗干扰性能得到提升,在控制器中融合干扰观测器(DOB),并对系统进行观测。
通过仿真表明,该控制策略对克服未知干扰有很大作用,不仅保证了炮控系统的静、动态特性,还有效地解决了滑模控制中特有的抖振现象,同时使系统的鲁棒性得到加强。
1 系统组成及数学模型的建立
1.1 系统组成及工作原理
炮控系统实质上是一种基于电液控制的伺服系统,负责控制坦克炮高低向调炮工作任务。它主要包括液压缸,旋转变压器,电液伺服阀,伺服放大器,负载身管和油泵,如图1所示。

在执行高低向调炮任务时,对炮控系统进行简化,如图2所示。
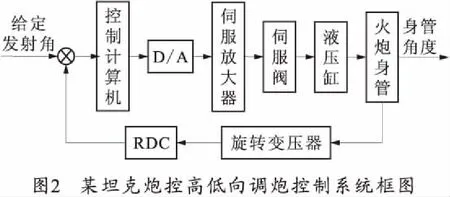
该系统的工作原理:根据作战需要,给定坦克炮身管的调炮角度,控制器收到调炮的指令后,经过计算机模块解算得出相应的控制量,将其传递给伺服放大板,信号经D/A模块和伺服放大板的调理后直接作用于电液伺服阀,通过控制电液伺服阀的开口大小和换向,控制液压缸的压力,该压力通过活塞缸筒作用于炮管负载,最终使坦克炮管到达预期的发射角度。旋转变压器对坦克炮管的实际位置进行测量,将测量到的信号传递给RDC模块转换得到数字信号后,传回控制计算机,从而形成一个完整的闭环回路。
1.2 系统模型建立
在建模之前先做如下假设:
1)忽略伺服阀的动态特性。
2)油源压力保持稳定。
3)管道和缸体内不会出现压力饱和现象。
4)液压油无泄漏。
5)忽略管道内压力损失和管道动态。
首先建立该电液伺服系统的流量方程,并通过余弦定理把炮管转角θ融入到方程中,最终经过拉氏变换后,可得:
FQ=K1U1Kbnb-Ct(p1-p2)=
(1)
式中:K1为电压放大系统;U1为输入控制电压;Kb为泵的排量梯度;nb为泵的转速;Ct为总泄漏系数;p1为负载压力;p2为补油压力;A为液压缸活塞面积;K1θ(θ)为液压缸活塞伸缩速度和身管角速度转换系数;θ为身管旋转角度;V0是压力为p1的液体容积;βe为有效体积弹性模数。
运用牛顿第二定律,对系统进行受力分析,可得该电液伺服系统的力矩平衡方程,并用拉氏变换对其进行转换,可得
T=(p1-p2)AL(θ)=Js2θ+Bmsθ+Gθ+TL
(2)
式中:J为转动惯量;L(θ)为液压缸活塞缸筒输出力对A点的力臂,L(θ)≈K1θ(θ);Bm为粘性阻尼系数;G为负载弹性刚度;TL为不平衡力矩,TL(s)=TG(s)-Tp(s)。

(3)
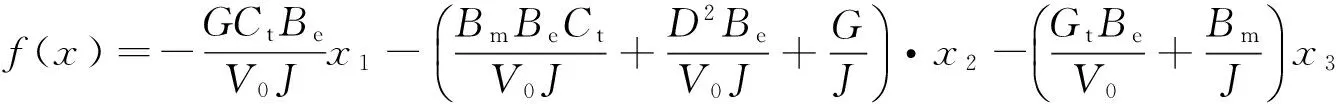
由于系统最终输出的是炮管的角度,故系统输出方程为
y=x1
(4)
2 基于DOB的RBF-SMC设计
2.1 滑模变结构控制器(SMC)设计
假设位置指令xd,则系统的跟踪误差为
e=xd-x1
(5)
取跟踪误差向量e为
(6)
将式(5)代入式(3),可得
(7)
根据滑模变结构控制理论,切换函数设计为
(8)
式中,c=[c1c21]T。

(9)
将式(7)代入到式(9),可得
(10)
故等效控制器设计为
(11)
为了保证滑模到达条件成立,即
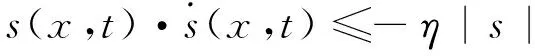
设计切换控制为
(12)
式中,K=D+η。
滑模控制律由等效控制项和切换控制项组成,即:
u=ueq+usw
(13)
然而在炮控系统中,由于带弹量的改变会导致系统的转动惯量J大范围的变动,并且随着工作条件的变化也会引起不平衡力矩TL、总泄漏系数Ct、粘性阻尼系数Bm的变动。因此,f(x),g,d(t)的各参数均是时变的,均是不确定参数,将导致等式ueq无法直接确定。故本文将用RBF神经网络的万能逼近特性来逼近参数f(x),g,d(t),用来替换等效控制项ueq,因此滑模控制律为
u=uRBF+usw
(14)
基于RBF神经网络滑模控制系统框图如图3所示。
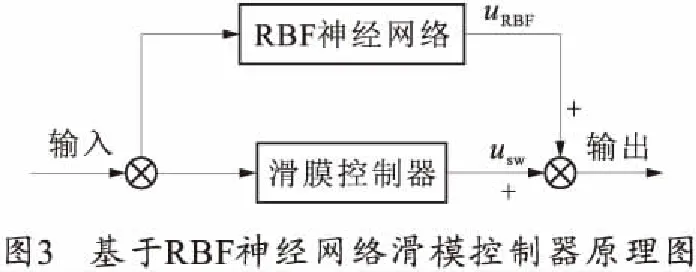
2.2 RBF神经网络控制设计
RBF神经网络是一种3层的前馈网络结构。笔者设计了一种2-7-1的神经网络架构,即输入层有2个参数,隐含层有7个神经元节点,输出层输出uRBF,如图4所示。
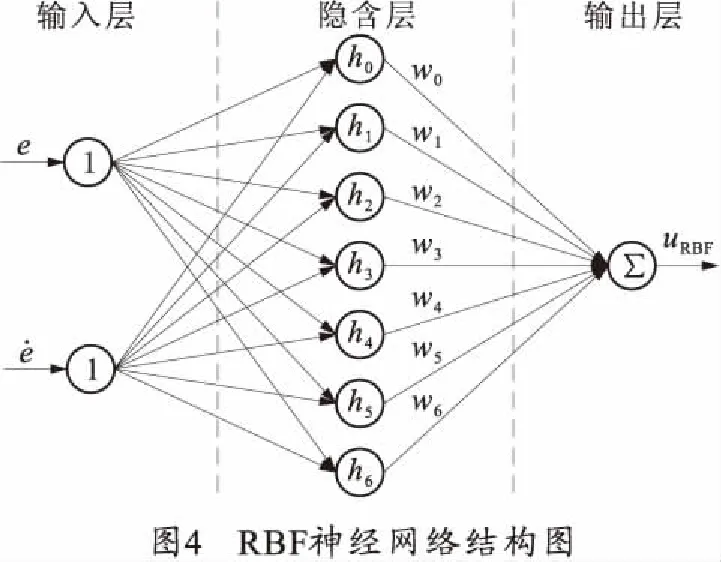
2)第2层:作为隐含层,采用高斯函数作为其基函数,设计了7个神经元节点,即H=[h0h1
h2…h6]T。
高斯函数结构为
(15)
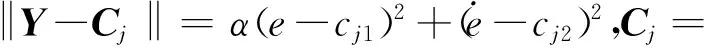
3)第3层:作为输出层,即输出uRBF。向量W=[w0w1w2…w6]是隐含层和输出层之间的权值,由图4可知:
(16)
2.3 干扰观测器设计
为了增强炮控系统的抗干扰性能和鲁棒性,设计了干扰观测器,以达到更好地控制炮控身管的平衡与定位的目的,并提高系统的跟踪性能[10-11]。
干扰观测器结构如图5所示,图中u是系统的输入信号;d是待测量的干扰信号;Gp(s)是实际系统模型;Gn(s)是标称模型;ξ(s)是系统的检测噪音;Q(s)是Q滤波器。
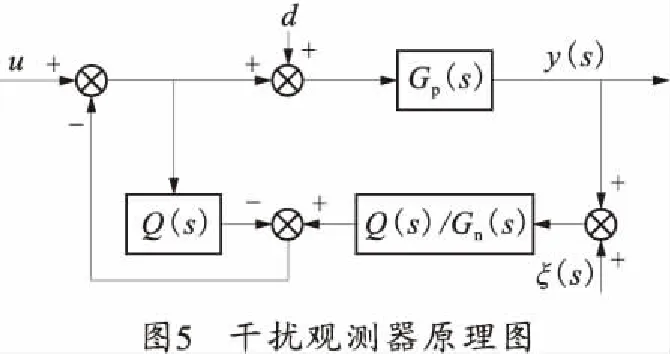
干扰观测器输出方程为y(s)=Guy(s)u(s)+Gdy(s)d(s)+Gξy(s)ξ(s)
(17)
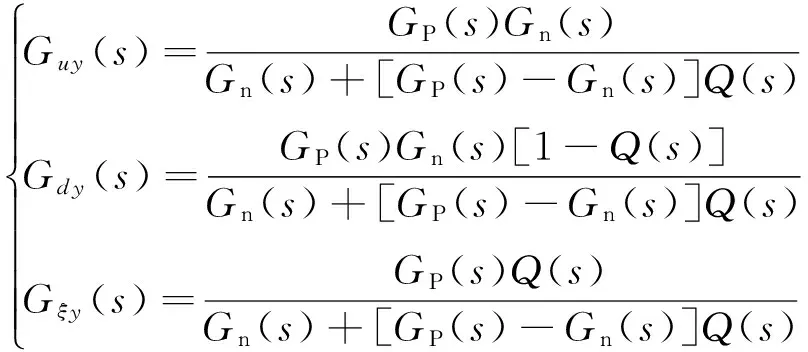
(18)
从式(18)可以看出,Q(s)的设计决定了干扰观测器的性能,在本文中,Q(s)设计为
(19)
式中:τ是时间常数。
2.4 控制器小结
综上所述,可知基于DOB的RBF-SMC控制策略的系统框图,如图6所示。

3 试验仿真
为了验证本文设计的控制算法,针对炮控身管系统进行仿真研究,系统的参数为:
Kb=4.224×10-7(m3·rad-1)/(°),K1=20,G=9.85×107(N·m)/rad,nb=104.72 rad/s,Bm=135(kN·m)/(rad·s-1),V0=11.18 dm3,Ct=1.5×10-13m3/(Pa·s),D=8.359 92 dm3/rad,Be=700 MPa。
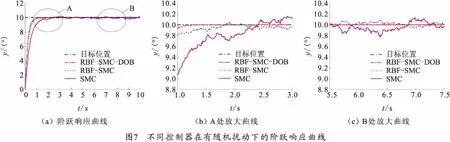
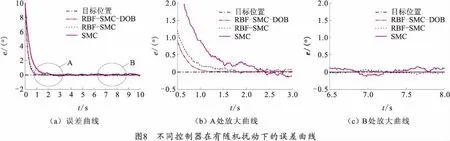
首先对系统的阶跃响应进行仿真,仿真过程分别与传统滑模控制(SMC),RBF神经网络滑模控制(RBF-SMC)进行对比,设定角度目标值为10°,进行仿真,仿真时间为10 s。对于外部的扰动采用一个角度在±0.3°范围内波动的随机信号进行模拟。其仿真曲线如图7、8所示。采用本文的控制策略,系统达到稳态的时间为1.3 s,无超调,基本无抖动,有较强的抗干扰能力,在RBF-SMC控制下,系统达到稳态的时间为1.5 s,存在较小幅度的抖动,而在SMC控制下,系统稳态时间为2.2 s,有超调现象,抖振很强烈。由此可见,在RBF-SMC控制基础上加上DOB观测器有助于提升系统的抗外界干扰能力,并提高系统的鲁棒性。 为了进一步验证所设计的控制策略对系统抗干扰性能及消除传统滑模变的抖振问题的作用,又对系统进行了正弦跟踪仿真试验。系统在做正弦跟踪时,加入以±0.5°范围内波动的随机干扰信号,其仿真结果曲线如图9、10所示。
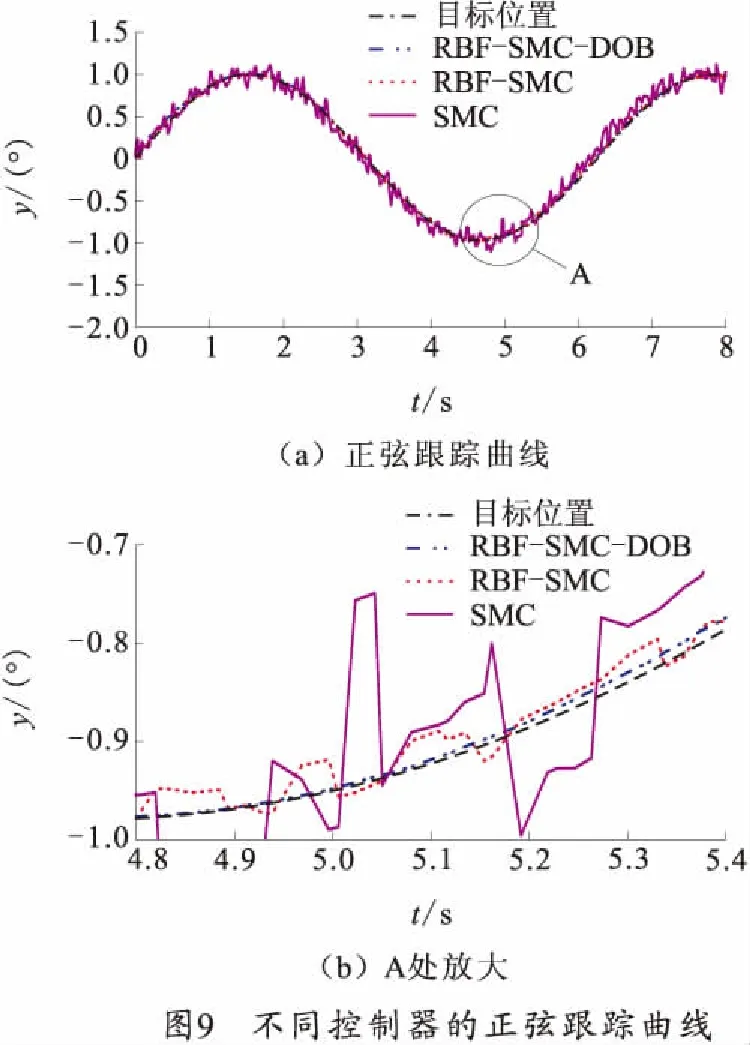

通过分析可知,采用SMC控制时,系统产生抖动,最大跟踪误差为0.27°;采用RBF-SMC控制时,系统抖动减小,最大跟踪误差为0.1°;而在RBF- SMC上加入DOB时,系统基本消除抖振,最大跟踪误差为0.03°。由此可见,本文的控制策略能更好地跟踪目标曲线,使系统的抗外界扰动能力得到提升,也较好地消除滑模控制存在的抖振,增强了炮控系统的鲁棒性。
4 结束语
笔者针对一种非平衡炮管的平衡定位问题,设计了一种基于DOB的RBF-SMC控制策略。通过仿真结果可知,该方法有效地抑制了传统滑模变结构(SMC)特有的抖振问题,较好地保持了滑模控制特有的抗摄动性能,并且对结构参数不确定性具有很强的鲁棒性,为电液伺服系统的非线性控制提供了试验依据。
References)
[1]田建辉. 火炮身管指向控制中的非线性问题研究[D]. 南京:南京理工大学, 2011:21-25. TIAN Jianhui. Research on the nonlinear problem in the pointing control of the gun[D]. Nanjing:Nanjing University of Science and Technology,2011:21-25. (in Chinese)
[2]LI Shuang, JIANG Xiuqiang. RBF neural network based second-order sliding mode guidance for mars entry under uncertainties[J]. Aerospace Science and Technology, 2015(43):226-235.
[3]王贞艳, 张井岗, 陈志梅. 神经网络滑模变结构控制研究综述[J]. 信息与控制, 2005,34(4):451-456. WANG Zhenyan, ZHANG Jinggang, CHEN Zhimei. A survey of research on neural network sliding mode variable structure control[J]. Information and Control, 2005,34(4):451-456. (in Chinese)
[4]王建敏, 董小萌, 吴云洁. 高超声速飞行器RBF神经网络滑模变结构控制[J].电机与控制学报, 2016,20(5):103-110. WANG Jianmin, DONG Xiaomeng, WU Yunjie. Hypersonic flight vehicle of sliding mode variable structure control based on RBF neural network[J]. Electric Machines and Control,2016,20(5):103-110.(in Chinese)
[5]YANG Jiye, CUI Yongfeng, CHEN Miaochao. Sliding mode control based on RBF neural network for parallel machine tool[J]. The Open Automation and Control Systems Journal,2014,6(1):575-582.
[6]MINHDUC T, HEEJUN K. A novel adaptive finite-time tracking control for robotic manipulators using nonsingular terminal sliding mode and RBF neural networks[J]. International Journal of Precision Engineering and Manufacturing,2016,17(7):863-870.
[7]NIU Jianjun, FU Yongling, QI Xiaoye. Design and application of discrete sliding mode control with RBF network-based switching law[J]. Chinese Journal of Aeronautics,2009,22(3):279-284.
[8]陈海忠, 高国琴. 两自由度并联机器人的RBF神经网络辨识滑模控制策略研究[J]. 机床与液压,2011,39(7):21-24. CHEN Haizhong, GAO Guoqin. RBF neural network identifying & sliding mode control of a 2-DOF parallel robot[J]. Machine Tool & Hydraulics,2011,39(7):21- 24. (in Chinese)
[9]王伟, 易建强, 赵冬斌. 一种新型神经网络滑膜控制器的设计[J]. 电机与控制学报, 2005,9(6):603- 606. WANG Wei, YI Jianqiang, ZHAO Dongbin. Design of a new type of neural network sliding mode controller[J].Electric Machines and Control, 2005,9(6):603-606. (in Chinese)
[10]李利娜, 窦丽华, 蔡涛,等. 基于干扰观测器的滑模变结构控制器设计[C]∥第29届中国控制会议论文集.北京:中国自动化学会,2010:5. LI Lina,DOU Lihua,CAI Tao,et al.Sliding mode varia-ble structure controller design based on disturbance observer[C]∥ Proceedings of the 29th Chinese Control Conference. Beijing: Chinese Association of Automation, 2010:5. (in Chinese)
[11]尹正男. 具有鲁棒性的最优干扰观测器的系统性设计及其应用[D]. 上海:上海交通大学,2012:15-23. YIN Zhengnan. Systematic design of optimal disturbance observer with robust performances and its application[D]. Shanghai:Shanghai Jiao Tong University,2012:15- 23. (in Chinese)

