基于自构建神经网络的舰载火箭炮内模控制

曾令梦，高 强，侯远龙，孙 战，蒋梦琴

(1.南京理工大学 机械工程学院，江苏 南京 210094; 2.北方自动控制技术研究所，山西 太原 030006)

舰载火箭炮作为火箭炮的分支，主要用于舰艇防空、反潜、对海上集群目标实行面杀伤、抢滩登陆火力支援等海上作战[1]。现代海战要求舰载火箭炮能够快速响应，持续稳定地跟踪运动中的目标，并提高舰载火箭炮的调炮精度。

内模控制( Internal Model Control，IMC)的实质是鲁棒控制，其设计思想是内模控制器取为过程逆模型，具有设计简单、响应快、鲁棒性强的特点[2]。神经网络具有非线性映射和强大的学习能力，主要用于复杂非线性、不确定性系统[3]。鉴于神经网络与内模控制的优点，很多学者对神经网络内模控制做了研究。文献[4]建立了基于Elman网络的航空发动机多变量内模控制系统，采用Elman网络建立发动机模型和内模控制器。文献[5]采用IMC的设计思路，应用神经网络的逼近能力，将其与自适应内模控制方案结合，设计出神经网络间接自适应内模控制器。

然而，神经网络结构的学习算法一般仅包括参数学习，并没有考虑结构学习，若隐含层神经元的个数选择过大，则会导致计算负荷很重，系统的实时性得不到保障；若数目选择过小，则导致学习性能不足以实现预期的控制性能[6]。为此，笔者将自构建神经网络结构用于内模控制系统的过程模型和内模控制器，神经网络的学习包括了结构和参数学习。在结构学习过程中，可根据输入数据及网络的结构在线创建和修剪不合适的隐含神经元，提高其学习能力和灵活性。通过仿真可知，本文的方法可使舰载火箭炮伺服系统具有良好的跟踪特性和抗干扰性，可提高其调炮精度。

1 舰载火箭炮交流伺服系统组成

火箭炮交流伺服系统结构图如图1所示。

舰载火箭炮交流伺服系统的工作原理：火控计算机经过弹道解算单元得到高低、方向角度，发送到随动控制计算机；随动控制计算机根据当前火箭炮实时角度和给定的目标角度，通过控制算法和D/A电路转换为模拟信号后，传递到伺服放大板、驱动器；驱动器通过速度反馈调节伺服电机的转速；最后经过减速器把机械动力传递到负载端，从而实现火箭炮的调炮动作。模拟负载(火箭炮发射架)的位置经过旋转变压器、RDC转换模块被实时反馈至计算机中，火箭炮交流伺服系统构成了一个完整的闭环控制系统，实现对目标的实时跟踪。

2 自构建神经网络原理

2.1 增加神经元描述

在训练过程中，针对每个输入样本xi，第j个隐含层神经元对输入样本的激励强度可以表示为输入数据属于该集群的度，可表示为

Θj=Hj

(1)

所有隐含神经元中对输入样本激励强度最大的值，定义为

(2)

式中，m(k)是在k时刻隐含层神经元的数目。

当输入数据远离现有的隐含神经元时，神经元对其激励偏小，使得最大激励强度值Θmax偏小，则需添加一个神经元，使得输入样本属于该集群，添加神经元需满足

Θmax≤Θth

(3)式中，Θth∈(0,1)，是一个预先定义好的激励强度阈值。

若Θth选取的值过大，则隐含神经元容易被添加;反之，Θth过小，隐含神经元很难被添加。在k+1时刻隐含神经元的数目增加为

m(k+1)=m(k)+1

(4)

新增加的隐含神经元的参数为

(5)

(6)

(7)

式中：xi为输入数据；σ为神经元中RBF(径向基函数)的宽度。

2.2 修剪神经元描述

在k+1时刻，第j个隐含神经元对输出的影响定义如下：

(8)

式中：Ij预先设定为1，j=1,2,…,m(k)；ρ为隐含神经元衰减阈值；τ为衰减速度。

随着隐含神经元对神经网络的影响程度达到一个很小的临界值时，说明该神经元对神经网络的输出基本无影响，此时可通过删除它来减轻神经网络学习过程中的计算负荷。删除隐含神经元时，需满足以下关系：

Ij≤Ith

(9)

Ith∈(0,1)为预先设定好的删除阈值。若Ith被设定得很大，则可以容易地消除神经元;反之，则不容易修剪隐含神经元。

3 自构建神经网络的内模控制设计

3.1 自构建神经网络内模控制

将神经网络与内模控制结合，充分发挥各自的优势，提升舰载火箭炮交流伺服系统的控制性能。自构建神经网络内模控制系统如图2所示。系统的内部模型和内模控制器均由RBF神经网络建立，并采用自构建的算法。

3.2 自构建神经网络的内部模型(NNM)设计

非线性系统的一般表达式为[7]

y(k+1)=f{y(k),y(k-1),…，y(k-n+1),u(k),…,u(k-m+1)}

(10)

式中：f(·)为非线性函数；y(k)，u(k)分别为系统模型的输出、输入，n、m为输出和输入的滞后时间。

利用神经网络的非线性映射特性，采用3层的RBF网络实现过程模型的建立[8]。

输入层

(11)

隐含层

(12)

输出层

(13)

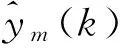
设计神经网络学习的目标函数为

(14)

用改进的梯度下降法调整参数[9]：

-ηe(k)Hj(k)

(15)

wj(k)=wj(k-1)+Δwj(k)+

α(wj(k-1)-wj(k-2))

(16)

(17)

bj(k)=bj(k-1)+Δbj+α(bj(k-1)-bj(k-2))

(18)

(19)

cji(k)=cji(k-1)+Δcji+α(cji(k-1)-cji(k-2))

(20)

在神经网络学习过程中，学习速率一般不变，不能实现神经网络的自适应。因此提出一种改进的梯度下降法，通过将学习速率与误差相关联，动态调节学习速率，以此获取最优学习率[9]。自适应学习速率η修改为

η(k)=(1-αΔE)η(k-1)

(21)

式中：η(k)、η(k-1)分别为学习率迭代时第k、k-1次的值；ΔE=E(k)-E(k-1)为误差增量。

通过误差增量ΔE对η的变化进行控制：ΔE>0，说明误差增大，参数的调整过大，需要减少；反之，当ΔE<0时，则η增大。α的取值范围一般为0.01～ 0.03。

自构建神经网络的参数学习步骤为： 将输入数据进行归一化处理； 对相关参数进行初始化； 输入一个训练样本； 对理想输出与实际输出之差求平方和，得到神经网络的输出误差；根据式(3)判断是否需要新增节点，根据式(9)判断是否需要删除节点；根据自适应率优化公式来获得新的学习率，并利用梯度下降法对权值、高斯函数中心和宽度进行调整；判断是否满足终止条件，若满足，则停止神经网络的学习；否则执行第3步骤。

3.3 自构建神经网络的内模控制器(NNC)设计

对于非线性系统，其逆模型可表示为

u(k)=f-1{y(k+1),y(k),…,y(k-n+1),u(k-1),…,u(k-m+1)}

(22)

式中，f-1(·)为f(·)的逆。

在控制系统中总是希望输出无偏差跟踪参考输入，因此y(k)=yr(k)，式(22)可表示为

u(k)=f-1{yr(k+1),yr(k),…,yr(k-n+1),u(k-1),…,u(k-m+1)}

(23)

u(k)=φ{yr(k+1),yr(k),…,yr(k-n+1),u(k-1),…,u(k-m+1),e(k)}

(24)

同样用3层RBF神经网络来实现上式的非线性函数。

输入层

(25)

隐含层

(26)

输出层

(27)

式中：rj(k)为输入层的输入；Gj(k)表示隐含层的第j节点输出；um(k)为模型的输出；dj为中心向量；sj为形状参数；m为隐含层神经元的个数；vj是隐含层到输出层之间的连接权矩阵。

过程逆模型的结构学习算法与过程模型的相同，都是采用改进的梯度下降法。

设计网络学习的目标函数为

(28)

用改进的梯度下降法修正网络参数：

(29)

vj(k)=vj(k-1)+Δvj(k)+α(vj(k-1)-vj(k-2))

(30)

(31)

dj(k)=dj(k-1)+Δdj+α(dj(k-1)-dj(k-2))

(32)

(33)

sji(k)=cji(k-1)+Δcji+α(cji(k-1)-cji(k-2))

(34)

4 仿真与结果分析

在自构建神经网络的内模控制中加入了前馈滤波器Gi和反馈滤波器Gf，有利于提高系统快速响应，抗干扰性，增强系统鲁棒性。

设定Gi=Gf=F，一般情况，滤波器取一阶形式，即

(35)

式中，λ∈(0,1)为可调参数。

利用SIMULINK搭建仿真模型图,对比内模控制和自构建神经网络(Self-constructingRecurrentNeuralNetwork,SRNN)内模控制两种控制器的效果如下。

4.1 施加阶跃信号的结果分析

给系统施加400mrad的阶跃输入信号，同时加入随机干扰，进行仿真。仿真结果如图3、4所示。

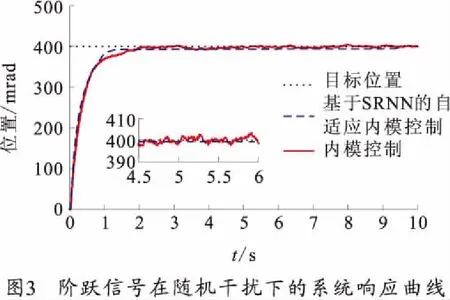
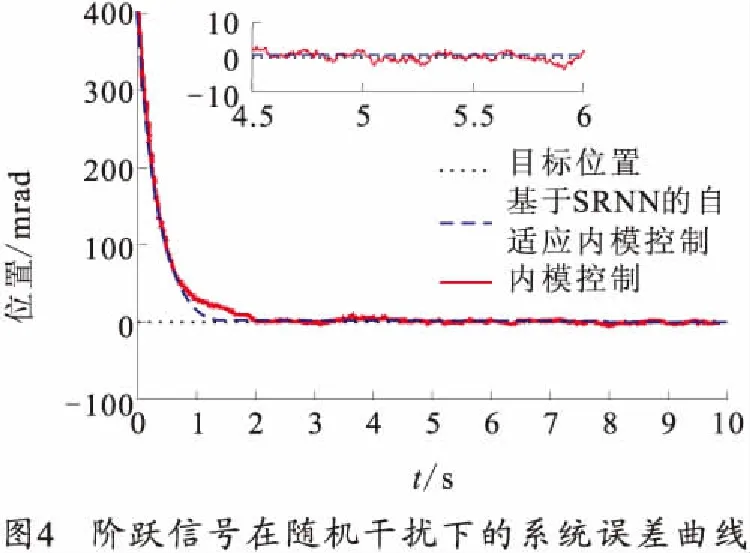
由图3、4可知：加入随机扰动后，采用内模控制时，系统稳定时间大约是2.2s，存在超调，稳态误差大约为4.188 8mrad。采用本文的方法进行控制时，系统稳定时间大约是1.6s，没有超调，无震荡，稳态误差很小，为0.460 8mrad。分析表明，输入信号为阶跃信号并加入随机干扰信号的情况下，自构建神经网络的自适应内模控制的控制响应更快，无超调，静态误差更小，抗干扰能力更强。

4.2 施加正弦信号时的结果分析

以正弦信号作为输入信号，测试系统的动态跟踪能力。采用y(t)=50 sin 2πt的正弦输入信号进行仿真，结果如图5～6所示。

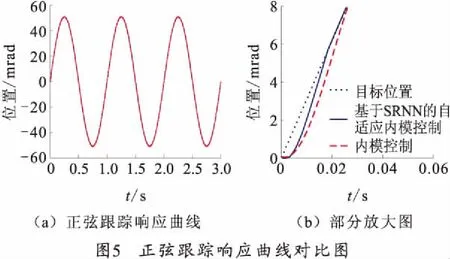
由图可知，输入信号为正弦时，采用传统的内模控制时，在0.3 s左右，误差下降到0.523 6 mrad,在0.5 s左右，系统跟踪误差最终稳定到0.523 6 mrad以内；而采用基于SRNN的自适应内模控制时，大约在0.2 s时，误差迅速下降到0.523 6 mrad，最终系统跟踪的动态误差稳定在0.314 2 mrad，动态跟踪过程中没有抖动现象。分析可知，采用自构建神经网络的自适应内模控制时，系统的动态跟踪能力很好，没有抖动现象，跟踪稳定，动态误差很小。

5 结束语

针对舰载火箭炮的非线性等特性，结合内模控制以及自构建神经网络的优点，设计了自构建神经网络内模控制器，对某舰载火箭炮交流伺服系统进行控制。实现了网络的结构和参数学习，使其可以根据需要进行在线调整，既不会过拟合也不会欠拟合，保证神经网络内模控制器的精度。通过仿真结果可知，基于自构建神经网络网络的内模控制比传统内模控制响应速度快，无超调，静态误差小，抗干扰能力强，并且具有良好的动态性能。

References)

[1]王雷. 防空火箭炮系统发射动力学研究[D]. 南京：南京理工大学, 2012. WANG Lei. Research on launch dynamics of antiaircraft rocket launcher system[D]. Nanjing：Nanjing University of Science and Technology, 2012.(in Chinese)

[2]LIU Dongbo, FUJII F. An adaptive internal model control system of a piezo-ceramic actuator with two RBF neural networks[C]∥International Conference on Mechatronics and Automation.Tianjin, China:IEEE Computer Society, 2014：210-215.

[3]喻宗泉. 神经网络控制[M]. 西安：西安电子科技大学出版社, 2009. YU Zongquan.Neural network control[M].Xi’an:Xidian University Press, 2009.(in Chinese)

[4]张鹏, 黄金泉. 航空发动机神经网络内模控制[J]. 航空动力学报, 2005,20(6): 1061-1065. ZHANG Peng,HUANG Jinquan. Neural network internal model control of aeroengine[J]. Journal of Aerospace Power, 2005, 20(6): 1061-1065.(in Chinese)

[5]梁义涛, 沈宪章, 刘新宇. 基于自适应神经网络内模控制的控制器设计实现[J]. 河南科学, 2004, 22(1): 80-83. LIANG Yitao, SHEN Xianzhang, LIU Xinyu. Design and implementation of controller based on adaptive neural network internal model control[J]. Henan Science, 2004, 22(1): 80-83.(in Chinese)

[6]YANG Y K,SUN T Y,HUO C L, et al. A novel self-constructing radial basis function neural-fuzzy system[J].Applied Soft Computing, 2013,13(5): 2390-2404.

[7]赵志诚, 王元元, 刘志远, 等. 一种自构建神经网络的内模控制方法[J]. 控制工程, 2014, 21(1): 111-115. ZHAO Zhicheng, WANG Yuanyuan, LIU Zhiyuan,et al. Internal model control method of self constructing neural network[J]. Control Engineering, 2014, 21(1): 111-115.(in Chinese)

[8]LIU Guohai, CHEN Linging, DONG Beibei, et al. RBF neural network application in internal model control of permanent magnet synchronous motor[C]∥ Advances in Neural Networks-ISNN 2011. Berlin ：Springer Berlin Heidelberg, 2011:68-76.

[9]MENSIA N, KSOURI M. Adaptive neural internal model control for complex process with delay[C]∥ International Conference on Communications, Computing and Control Applications. Hammamet, Tunisia：IEEE, 2011:1-7.