从归纳到贯通

李万斌

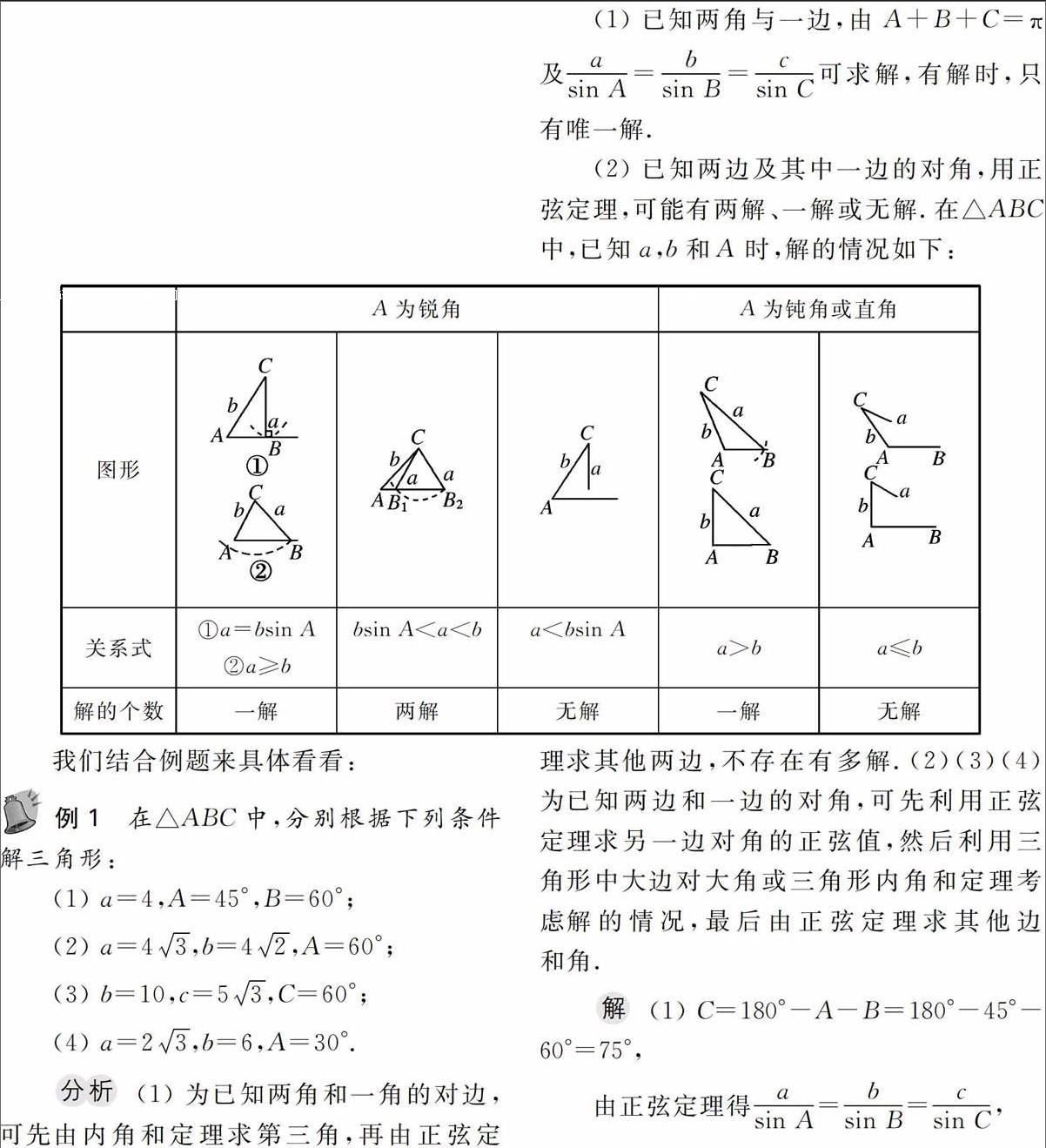
我们知道，三角形的三条边和其三个内角称为三角形的六个基本组成元素，解三角形即是求解剩下未知元素的过程，在复习时我们应该查漏补缺，力求将知识重点和难点梳理清楚，理解透彻，解三角形中，如何判断三角形的解的个数，是我们应该着重掌握的，下面我们结合正弦定理的使用进行探究。

感悟求解测量问题的关键是把测量目标纳入到一个可解三角形中，三角形可解，则至少要知道这个三角形的一条边长，解题中注意各个角的含义，根据这些角把需要的三角形的内角表示出来，注意不要把角的含义弄错，不要把这些角与要求解的三角形的内角之间的关系弄错，实际问题中的三角形的解的个数有一定的特殊性，需要我们全方位考虑，时刻保持警惕。

综上，我们可以看到，利用正弦定理可以处理诸如解三角形及其实际应用问题，事实上，灵活使用正弦定理还可以处理更多的问题，如判断三角形形状及与三角形面积相关等，关键是要能精准地判断出三角形解的情况，这需要同学们更加深刻体会定理的内涵与外延，尤其是准确区分不同情况下使用定理的条件。

题型或者解法归纳后仍只是囿于形式，只有把前因后果梳理通透，形式与本质融会贯通，将所学所感化为真正的自己的“武器”，才能圆满完成复习的任务。