包含磁力齿轮的位置伺服系统的极点配置与积分校正控制
曹家勇,张婧茹,代欣,梁庆华
包含磁力齿轮的位置伺服系统的极点配置与积分校正控制
曹家勇1,张婧茹2,代欣2,梁庆华2
(1. 上海应用技术大学机械工程学院,上海,201418;2. 上海交通大学机械与动力工程学院,上海,200240)
为克服磁力齿轮的低刚度特性,提高伺服系统动态性能和抗干扰能力,采用以输出位置作为状态反馈构成全闭环控制系统的策略。建立既考虑磁力齿轮的动力学特性,又考虑摩擦负载和外界负载的综合动力学模型,进而得到系统的频域表达和状态空间表达。利用极点配置法,合理选择闭环系统主导极点,并设定状态反馈系数向量,以获得预想的系统性能。为进一步增强系统的抵抗负载波动能力,引入积分校正环节对位置误差信号进行积分运算,构建基于积分校正方法的控制系统。对所建立的2类控制系统进行数值仿真。研究结果表明:2种控制方法均能使直线滑台快速而准确地到达指令位置,实现对输入信号的良好跟踪。但含积分校正器控制系统具有更好的抗干扰能力和定位精度,更适用于具有大波动负载和外界干扰的场合。
伺服系统;磁力齿轮;数学建模;极点配置
磁力齿轮的非接触传动模式带来了加工成本低廉、无机械接触失效、便于维护、固有的过载保护等优势。随着高性能永磁材料和新型结构的发展,现在的高性能磁力齿轮的转矩密度和传递效率已经能与机械齿轮箱相媲美,在工程上具有广阔的应用前景[1−5]。磁力齿轮在伺服系统中应用有2种途径:一种是替代伺服系统中常见的行星齿轮;另一种使磁力齿轮与电机部件及磁场融合,形成一种类似于直接驱动的新型驱动元件(被称作“伪”直驱电机)[6−7]。但是,不管应用形式如何变化,克服磁力齿轮的高弹性特点和非线性传力特性,保证系统的动态响应和稳态精度,是实现磁力齿轮在伺服系统中应用的关键。WANG等[7]分析了一类含磁力齿轮的“伪”直驱电机的高速转子和低速转子相互作用特性,建立了磁力齿轮的双惯性传动系统模型,采用基于状态观测器的全状态反馈方法,实现了磁力齿轮的速度伺服控制。MONTAGUE等[8]采用PI控制算法,结合ITAE参数优化方法,实现了对磁力齿轮的速度伺服控制。MONTAGUE等[9]提出了磁力齿轮位置伺服控制的PD算法,为了提高系统的稳态精度,还在系统中引入了具有非线性校正作用的双观测器,验证了磁力齿轮的非线性特性可以在应用中被克服。BOUHERAOUA等[10]讨论了“伪”直驱电机的综合系统模型,比较了PI,IP和状态反馈3种控制策略,认为状态反馈控制能够使系统达到最好的系统阻尼和鲁棒性。MONTAGUE等[11−12]又实现了磁力齿轮的反馈线性化伺服控制、带观测器的状态反馈控制和只具有1个位置传感器的伺服控制方法[6]。目前磁力齿轮伺服控制仅限于研究电机和磁力齿轮构成的半闭环控制系统,基本未涉及执行机构负载特性(比如执行机构的惯性、摩擦特性等)对系统性能的影响问题。鉴于此,本文作者将磁场调制式磁力齿轮应用于一类典型的机械伺服系统,即直线滑台伺服系统,探讨其控制器设计、系统特性分析等问题。构建以滑台位移为被测量的全闭环控制系统,建立包含磁力齿轮的直线滑台伺服系统的数学模型。在此基础上,利用极点配置法确定系统状态反馈的系数,并且引入积分器校正环节,以抑制外部干扰对系统的影响[13]。

图1 含磁力齿轮直线滑台伺服传动系统简单示意图
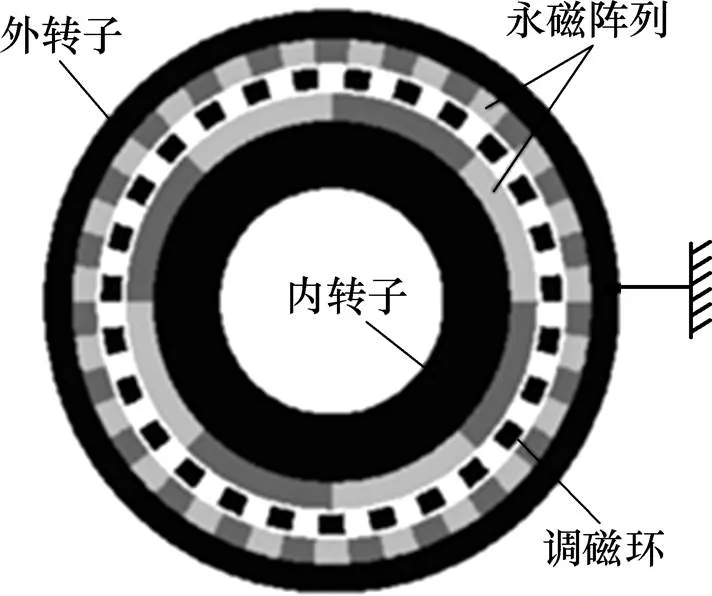
图2 磁场调制式磁力齿轮结构形式
1 包含磁力齿轮伺服系统的建模
包含磁力齿轮的直线滑台伺服传动系统构成如图1所示,其由伺服电机、磁力齿轮、线性模组等组件构成。伺服电机输出的运动通过磁力齿轮减速后传递给线性模组,线性模组中的丝杆螺母副实现转动运动到直线平移运动的转换。系统中的磁力齿轮原理结构如图2所示,这是一类磁场调制式磁力齿轮,因具有很高的转矩密度,受到广泛关注。磁场调制式磁力齿轮由3个同心部件构成:最内层的是高速内转子,由内转子铁心和附着于内转子铁心外圆柱面上的永磁体构成;中间层是调磁环,由高导磁材料和非导磁材料间歇排布的构成;最外层是低速外转子,由外转子铁心和附着于外转子内圆柱面的一系列永磁体构成[1]。在实际使用中通常将调磁环固定,高速的内转子在2套永磁体形成磁场的相互作用下,将动力传递给低速的外转子。
为获得含齿力齿轮的伺服传动系统动力学模型。首先,采用简化假设认为,伺服电机本身具有良好的伺服特性,即伺服电机能够精确地复现驱动器的给定指令,这一假设的合理性和有效性在文献[8,14]中得到理论和实验的验证。其次,将磁力齿轮等效成由2套理想齿轮副和1副理想磁力联轴器构成[8, 14],所谓“理想”指的是相关零件无转动惯量,至于实际系统的转动惯量,采用集中惯量等效的办法来体现。最终得到整个系统的动力学模型如图3所示。图3中:M和L分别为高速轴的集中转动惯量和低速轴的集中转动惯量;为线性模组滑台的质量;扭转弹簧代表理想磁力联轴器。磁力联轴器传递的转矩用C表示,实际系统中C呈现周期非线性限制。但是,在正常载荷范围内,C可近似看成随磁力联轴器输入和输出转角差D线性变化,即
C=(MM−sL)
其中:为磁力联轴器的线性传动刚度;M为输入轴的转动角度;L为输出轴的转动角度;M和s分别为内转子磁极对数和调磁环极靴个数。

图3 传动系统等效双惯性模型
根据力矩平衡原理,得到系统的运动方程式如下:
其中:a为丝杆螺母施加于丝杆上的阻力矩,由负载平台所受的水平外载荷L和平台运动惯性力共同产生,即

为负载质量(包含平台和平台上面负载),kg;为丝杠导程,m;为进给丝杠的传动效率。
进行拉氏变换,得到
将外载荷L视作外界干扰项,令L=0,又()=L(),求解上述方程组得到系统的传递函数:
假设输入量为0,计算只在扰动量作用下的响应可以得到

其中:M()和L()分别为电机侧和负载侧的角位移,rad/s;EM()为电机驱动力矩的频域信号,N·m;M和L分别为电机侧和负载侧的转动惯量,kg·m2。
根据式(5)和式(6)绘制直线滑台传动系统方框图如图4所示。

图4 直线滑台传动系统方框图
2 基于极点配置法的控制器设计
闭环系统动静态性能与系统闭环极点在根平面上的位置紧密相关,因此,一种直接有效的闭环设计方法就是引入某种控制器,实现将闭环系统所有极点配置到理想位置,即极点配置方法[15]。带有输入变换的状态反馈系统图如图5所示。图5中:为状态反馈增益,根据极点配置法确定;为增益调节。
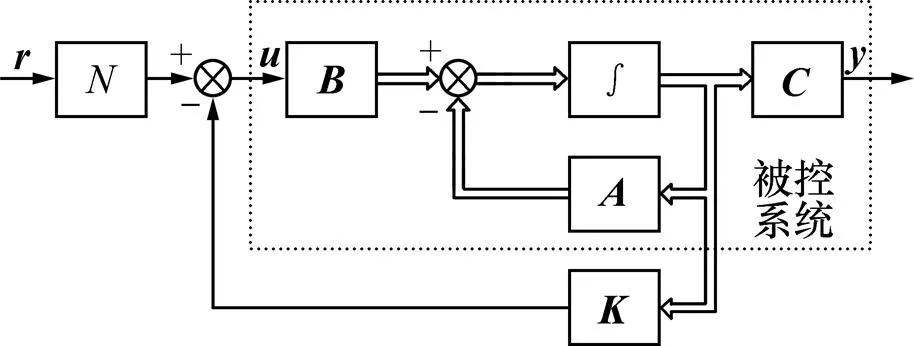
图5 状态反馈原理图
定义系统的状态变量=[1234]T=[]T,对象输入=EM,对象输出=1=,则系统的状态方程可表示为如下形式:
=(9)
式中:

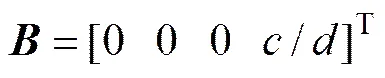

极点配置设计方法的前提是选择好希望的闭环极点的位置。选择这一类极点的方法,主要依据对象的阶次以及控制要求等,一般根据经验选择。基于极点配置理论,可以知道该种类型的控制方法作用于系统中,得到的闭环极点个数不会超过对象的阶次4,因此,这里设计4个期望的闭环极点。基于根轨迹设计中的经验,闭环极点的设计思路是先对1对共轭主导极点进行配置,再选择其余次极点,使其处于远离主导闭环极点的左方。一般来说,在复平面上当某极点距离虚轴的距离为主导极点距离虚轴距离的5~10倍时,就认为该极点为一次极点。其中主导闭环极点可根据系统希望的阻尼比以及无阻尼自然频率n来确定。这里,根据经验选择相对阻尼=0.707。带宽表示系统跟踪正弦输入信号的能力,在这里选择系统的带宽为10 Hz,因此选择极点的自然频率也为n=10 Hz,于是得到2个共轭主导极点1和2为。
接着探讨输入变换放大器的取值。由系统的开环传递函数和所配置的极点可知,极点配置之后系统的闭环传递函数为

其中:ref()为无增益调节时直线滑台的期望位置。
根据终值定理,对于阶跃输入,即ref()=1/,有


于是,选择为

3 引入积分器校正状态反馈
以上讨论未考虑系统的外部干扰,然而在实际过程中外界对系统产生的干扰是难以避免的,会导致系统瞬间产生波动,并且恢复稳态时往往造成稳态偏差的产生,不能理想地跟随输入指令。将经典控制理论中比例积分控制的思想引入本文描述系统中,构造如图6所示的状态反馈加积分器校正的输出反馈系统。图6中:维列向量为扰动输入,为参考输入;,和分别为维,维和维列向量;,和分别为×,×和×实数矩阵;1和2分别为×和×实数矩阵。将个积分器生成的作为附加状态向量,与原被控系统可构成被控系统增广的动态方程,
增广系统状态反馈控制律为

图6 引入积分器校正的闭环控制原理图
式(11)中的第1项−1为被控系统的普通状态负反馈,第2项2为改善稳态性能而引入的误差的积分信号。只有式(11)所描述的+维增广系统状态完全能控,才可采用式(10)所示的状态反馈改善系统的动态和稳态性能。容易证明,增广系统能控的充要条件为原被控系统能控,且。
将式(11)代入式(10)可得状态反馈增广系统(见图6)的动态方程为
因此,只要1和2选得使式(12)的特征值均具有负实部,则图6所示闭环系统可消除阶跃扰动及阶跃参考输入作用下的稳态误差。选取期望的闭环极点:
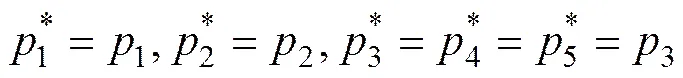
同样可以利用解析法求得1和2。
4 仿真结果
基于上述设计原理,在Matlab/Simulink环境中建立仿真模型,模型参数如表1所示。
图7所示为状态反馈系统和额外引入积分器校正的系统的单位阶跃响应曲线,它们过渡过程的品质特性如表2所示。从图7可以看出:在没有外界干扰的情况下2类系统都具有较好的阶跃响应,但相比较而言,单纯状态反馈系统的超调量较大,且相应的上升时间、峰值时间以及调整时间较长。

表1 控制对象模型参数

1—有积分器系统;2—无积分器系统。
图7 2类系统阶跃响应特性
Fig. 7 Step responds of two control systems with and without integral compensation
图8所示为阶跃负载作用下2种系统阶跃响应图。针对本文系统,假设系统在=0.5 s时系统突然受到500 N的外力干扰,该情况模拟了作业过程中工况变化(如刀具与工件的接触)对系统的影响。从图8可以看出:引入积分器的系统对阶跃信号干扰有明显的抑制作用。比较2个系统的抗扰性能指标如表3所示,其中动态降落是指系统稳定运行时,突加一定数值的扰动后引起输出的最大降落值,用输出量原稳态值的百分比来表示。

表2 2类系统阶跃响应特性比较

表3 2类系统抗扰性能指标比较

1—有积分器系统;2—无积分器系统。
图8 阶跃信号干扰下2类系统的响应曲线
Fig. 8 Responds to step disturbance of two control systems with and without integral compensation
图9所示为不同幅值交变信号作用在2个系统上的响应情况,假设系统受到一基值为0、幅值为500 N、频率为20 Hz的正弦脉动信号干扰。从图9可以看出:响应结果为在原响应的基础上,再叠加了1个同频率的负载脉动,但是明显可以看出引入积分器的系统对该种类型的扰动信号有抑制能力较强。图10和图11所示分别为不同频率负载作用下,无积分器和有积分器系统的响应情况。从图10和图11可以看出:无积分器系统对高频扰动有较好的抑制性能,对相对低频的则难以抑制。而加入积分器的系统对各种频率均有较好的抑制性能。

频率/Hz:1—10;2—100。
图9 正弦信号干扰下2类系统的响应曲线
Fig. 9 Responds to sinusoidal disturbance of two control systems with and without integral compensation

频率/Hz:1—10;2—100。
图10 不同频率信号干扰对无积分器系统的影响
Fig. 10 Effect of sinusoidal disturbances with different frequencies on control system without integral compensation

频率/Hz:1—10;2—100。
图11 不同频率正弦信号干扰对引入积分器系统的影响
Fig. 11 Effect of sinusoidal disturbance with different frequencies on control system with integral compensation
5 结论
1) 将磁力齿轮引入到位置伺服系统中,研究其系统建模和全闭环控制问题。建立了包含磁力齿轮的直线伺服滑台的综合数学模型,该模型不仅体现了磁力齿轮的动力学特性,还考虑了滑台摩擦特性和负载状况。基于极点配置法,分别设计了不含积分校正器和含积分校正器的2种控制系统。
2) 2种控制方法均能使直线滑台快速而准确地到达指令位置,实现对输入信号的良好跟踪。但是,对于具有大波动负载和外界干扰的场合(如切削加工机床),含积分校正器控制系统具有更强的抗干扰能力和更高的定位精度。研究结果为进一步拓展磁力齿轮在伺服系统的应用提供了良好的思路。
[1] ATALLAH K, HOWE D. A novel high-performance magnetic gear[J]. IEEE Transactions on Magnetics, 2001, 37(4): 2844−2846.
[2] SHAH L, CRUDEN A, WILLIAMS B W. A magnetic gear box for application with a contra-rotating tidal turbine[J]. IEEE Transactions on Magnetics, 2011, 47(2): 431−438.
[3] GULDAGAD M N, ANAND P G. The design of power tansmission system through “the cycloid magnetic gear” for Hybrid Vehicles[C]//14th National Conference on Machines and Mechanisms. Durgapur, India, 2009: 468−470.
[4] JIAN L, CHAU K T. A novel electronic-continuously variable transmission propulsion system using coaxial magnetic gearing for hybrid electric vehicles[J]. Journal of Asian Electric Vehicles, 2009, 7(2): 1291−1296.
[5] MONTAGUE R G, BINGHAM C M, ATALLAH K. Magnetic gear dynamics for servo control[C]//Proceedings of the 15th IEEE Mediterranean Electrotechnical Conference. Valletta, Republic of Malta, 2010: 1192−1197.
[6] BOUHERAOUA M, WANG J, ATALLAH K, et al. Speed control for a pseudo direct drive permanent magnet machine with one position sensor on low-speed rotor[C]//Electric Machines & Drives Conference. Chicago, USA, 2013: 986−992.
[7] WANG J B, ATALLAH K. Modeling and control of ‘pseudo’ direct-drive brushless permanent magnet machines[C]//IEEE International Electric Machines & Drives Conference. Miami, USA, 2009: 870−875.
[8] MONTAGUE R G, BINGHAM C M, ATALLAH K. Characterisation and modelling of magnetic couplings and gears for servo control systems[C]//5th IET International Conference on Power Electronics, Machines and Drives. Brighton, UK, 2010: 1−6.
[9] MONTAGUE R G, BINGHAM C M, ATALLAH K. Dual-observer-based position-servo control of a magnetic gear[J]. IET Electric Power Application, 2011, 5(9): 708−714.
[10] BOUHERAOUA M, WANG J, ATALLAH K, et al. A complex frequency domain analysis of a closed loop controlled pseudo direct drive[C]//2012 International Conference on Electrical Machines. Marseille, France, 2012: 2428−2434.
[11] MONTAGUE R, BINGHAM C. Nonlinear control of magnetically-geared drive-trains[J]. International Journal of Automation and Computing, 2013, 10(4): 319−326.
[12] BOUHERAOUA M, WANG J, ATALLAH K. Design and implementation of an observer-based state feedback controller for a pseudo direct drive[J]. IET Electric Power Application, 2013, 7(8): 643−653.
[13] RAMLI M S, RAHMAT M F, NAJIB M S. Design and modeling of integral control state-feedback controller for implementation on servomotor control[C]//6th WSEAS International Conference on Circuits, Systems, Electronics, Control & Signal Processing. Cairo, Egypt, 2007: 208−213.
[14] MONTAGUE R, BINGHAM C, ATALLAH K. Servo control of magnetic gears[J]. IEEE-ASME Transactions on Mechatronics, 2012, 17(2): 269−278.
[15] OGATA K, 卢伯英, 佟明安. 现代控制工程[M]. 北京: 电子工业出版社, 2011: 781−791. OGATA K, LU Boying, TONG Mingan. Modern control engineering[M]. Beijing: Electronic Industry Press, 2011: 781−791.
(编辑 杨幼平)
Control strategy of servo positioning system with magnetic gears based on pole assignment and integral compensation
CAO Jiayong1, ZHANG Jingru2, DAI Xin2, LIANG Qinghua2
(1. School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 201418, China;2. School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)
The magnetic gears have the characteristics of low stiffness, which is normally regarded as the main barrier for their widespread application in the systems with high-bandwidth dynamic transients. A closed loop control strategy for the linear positioning system with magnetic gears was proposed. A comprehensive dynamic mathematical model, which takes into account the dynamic of magnetic gears, as well as the frictional load and external force, was proposed. Based on the dynamic model, a frequency-domain expression and a state-space expression were both obtained. For realizing the desired dynamic response, a pole placement algorithm was used. An extra integral regulation was introduced to strengthen the ability of rejecting the load disturbances. The results show that those two types of controllers can adjust the position of the linear stage accurately and fast. The second controller with integral regulation has a higher anti-disturbance ability and positioning accuracy.
servo system; magnetic gear; mathematical modelling; poles placement
10.11817/j.issn.1672-7207.2016.12.012
TM301.2;TH132.4
A
1672−7207(2016)12−4041−07
2015−12−04;
2016−03−03
国家自然科学基金资助项目(51175325);上海应用技术大学引进人才科研启动基金资助项目(2015年)(Project(51175325) supported by the National Natural Science Foundation of China; Project(2015) supported by Shanghai Institute of Technology Research Foundation for Scholars)
曹家勇,副教授,硕士生导师,从事新型驱动与运动控制、磁力传动技术和机电一体化技术的研究;E-mail:caojy@sit.edu.cn

