列车移动荷载下饱和软黏土地基的长期沉降计算

陶明安，沈扬，王鑫，王保光，杜文汉



列车移动荷载下饱和软黏土地基的长期沉降计算

陶明安1, 2，沈扬1，王鑫1，王保光1，杜文汉1

(1. 河海大学岩土力学与堤坝工程教育部重点实验室，江苏南京，210098；2. 铁道第三勘察设计院集团有限公司，天津，300142)

借助空心圆柱扭剪仪开展偏应力空间中主应力轴心形线旋转路径的室内模拟，建立列车移动荷载引发的主应力轴心形旋转路径下土体的塑性累积模型和孔压模型；在动力有限元中引入等效移动列车荷载，并结合分层总和法的思想，建立高速列车移动荷载作用下饱和软黏土地基的长期沉降计算方法，进一步研究交通荷载下地基软土的长期变形规律。研究结果表明：总沉降量随着振次的增加而增大，其增大速率迅速减小，并在振动约250万次时出现拐点，总沉降速率趋于稳定，此时沉降量占4 a总沉降量的90%以上；土体总沉降量随着深度的增加而不断减小，整体沉降主要发生在距地面5 m以上部分，该部分的沉降量占总沉降量的95%以上；随着列车运行速度的增大，地基土层的总沉降增大，当列车速度超过临界速度时，地基的总沉降量反而大幅度减小。

列车；移动荷载；主应力轴心形旋转；塑性累积模型；孔压模型；长期沉降

目前，国内许多高速铁路建设在分布着大量淤泥、淤泥质黏土等软弱土的东部沿海地区。国内外研究表明，软土地基在长期列车荷载作用下，会产生较大的塑性累积变形直接影响列车的正常运营与安全[1]。原京沪线铁路沪宁段、沪杭铁路等建成初期客车速度为40~50 km/h，随着铁路速度提高到160 km/h甚至200 km/h后，亦产生了较大的累积沉降及严重路基病害。列车荷载引起地基中土单元体的应力状态及应力路径改变，不同于传统基坑开挖过程中应力路径的改变和机械振动、地震、波浪荷载等引起土单元体的应力状态，其应力特征为主应力方向连续旋转与剪应力幅值耦合变化的心形线应力路径[2]，该路径条件下土的变形特性非常复杂，表现出与常规振动三轴和振动扭剪等循环应力路径明显不同的特性。GRABE等[3]发现交通荷载引发的主应力轴旋转会加速永久变形的开展速度；钱建固等[4−5]发现不排水条件下心形循环加载将诱发软黏土更大的累积轴向应变和累积孔压，且伴随着初始动应力比的增加，二者差异性更为明显。陶明安等[6−7]提出了3类空心圆柱扭剪仪模拟交通荷载引发的主应力轴旋转路径的加载方法，并研究了不同主应力旋转路径下土体变形与强度的发展规律。研究交通荷载作用下软土地基土体长期沉降变形计算模型主要分为理论计算方法和经验计算方法。当循环加载次数达到几十万次数量级时，理论计算方法会产生巨大的计算量，因此，工程实际中应用更多的是基于经验模型的实用简化计算方法[8−9]。列车荷载下地基土体的长期沉降的准确计算要基于列车荷载应发特殊应力状态下土体的动力特性成果，但以往的经验计算模型所依据的相关室内动力试验极少与实际荷载下地基土中应力路径与应力状态相吻合。本文作者将建立交通荷载下土体累积变形与累积孔压的预测模型，在动力数值计算中实现等效移动列车荷载的施加，并得到地基中的动力分布情况，采用分层综合法的思想，初步建立高速列车荷载作用下地基软土的累积变形计算方法，并进一步研究高速交通荷载作用下软土地基的长期沉降变形机理。

1 轴向塑性累积变形预测模型

1.1 试样制备

所用黏土取自南京河西地区，采用改进真空预压制备技术制作的性质均一重塑土样开展试验，具体的制样方法为：原土烘干过筛，加水搅拌均匀配成1.8倍液限泥浆，注入特制真空抽吸装置中，静置1 h后，以30，60和90 kPa的3级施加真空负压36 h。与以往的制样方法相比，改进真空预压制样技术通过三瓣渗透排水体与多个装置同时制作，在缩短制样周期与避免试样二次削切与浪费的同时，在含水率与密实度等方面具有更好的一致性与均匀性。试样的基本物理性质指标见表1。

表1 试样的物理性质指标

采用河海大学与英国GDS联合开发空心圆柱扭剪仪(HCA)模拟不同主应力轴旋转模式，独立控制动态轴力和扭矩，保持内、外压在动力变载过程中恒定，在试验过程中可使中主应力方向始终维持在径向，大主应力1和小主应力3的作用方向在垂直于径向的切平面内发生连续旋转，即应力主轴在平面内旋转。

1.2 试验方案

空心圆柱扭剪仪标准试样高度×外径×内径为200 mm×100 mm×60 mm，通过自定义波输入，便可以实现不同主应力轴旋转模式的加载，具体加载方法见文献[6]。这里给出实现不同主应力方向变化模式下轴力与扭矩的加载波形，见图1。图1中，为时间；为周期。

试样安装完成后，进行反压饱和。当测得饱和度大于0.95 时，认为试样已饱和。由于本试验重塑黏土试样的渗透系数小，固结时必须采用双面排水和试样周围贴滤纸条的方法，使试样既能通过上下两端透水石排水，又能通过滤纸条排水，加速固结过程。当排水量变化小于0.1 cm3/h时认为固结已经完成。试验施加动应力水平采用初始动应力比表示，即=/0(其中：=(1−3)/2，0为初始有效平均主应力)，具体的试样方案见表2，实测应力路径如图2所示(其中：z为垂向正应力；σ为切向正应力；τ为垂直于径向切应力)。

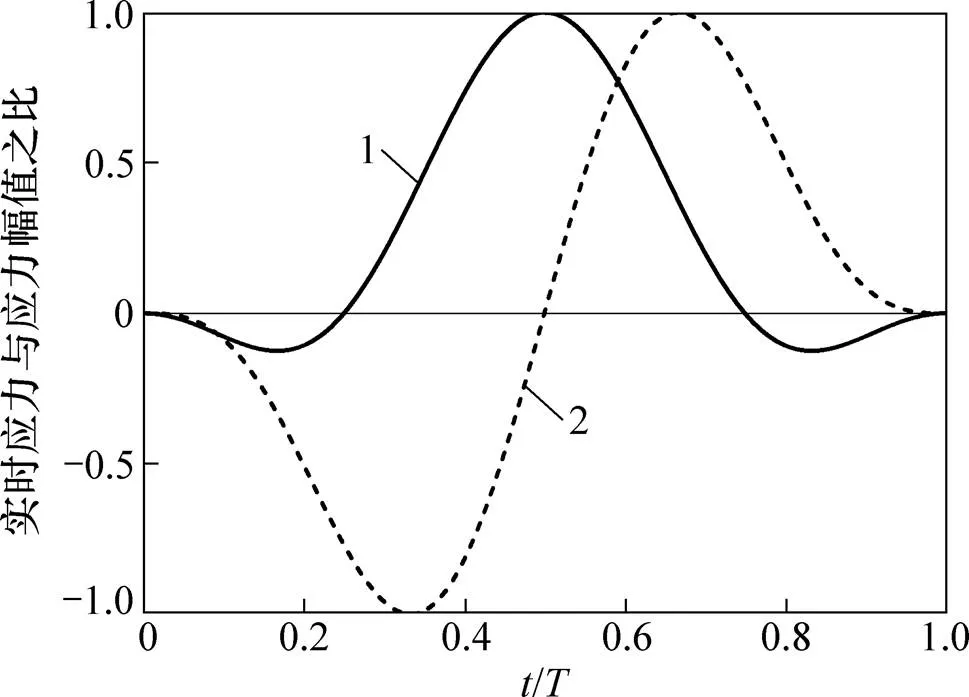
1—轴力加载波形；2—扭矩加载波形。

图1 HCA模拟主应力心形旋转路径的加载波形

Fig. 1 HCA load waveforms under principal stress rotation

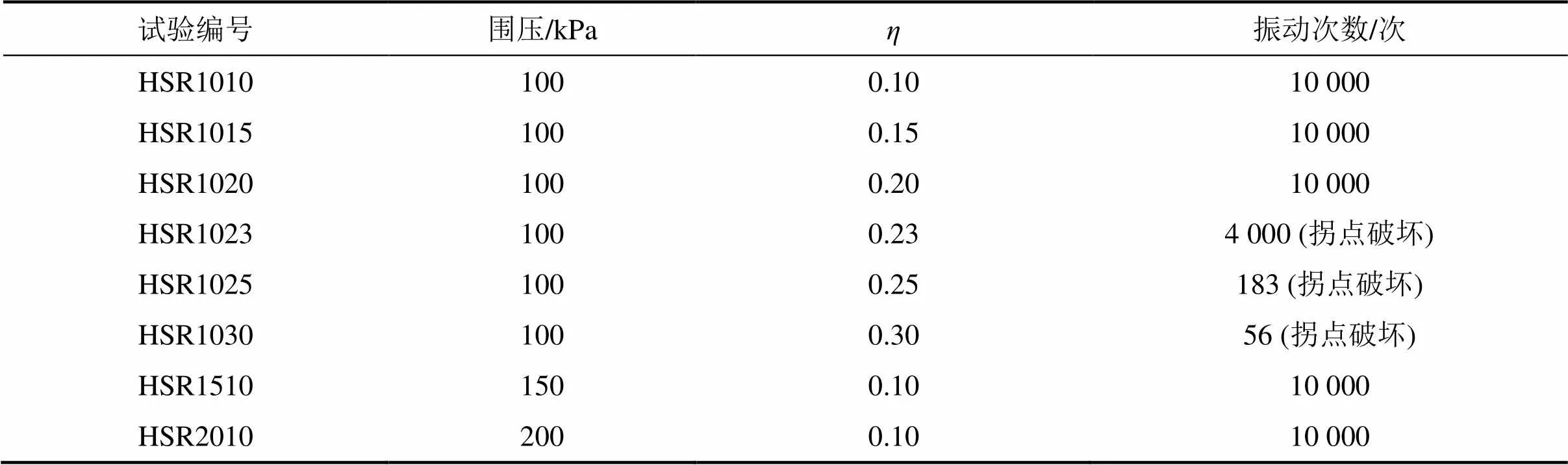
表2 主应力轴心形旋转路径试验方案

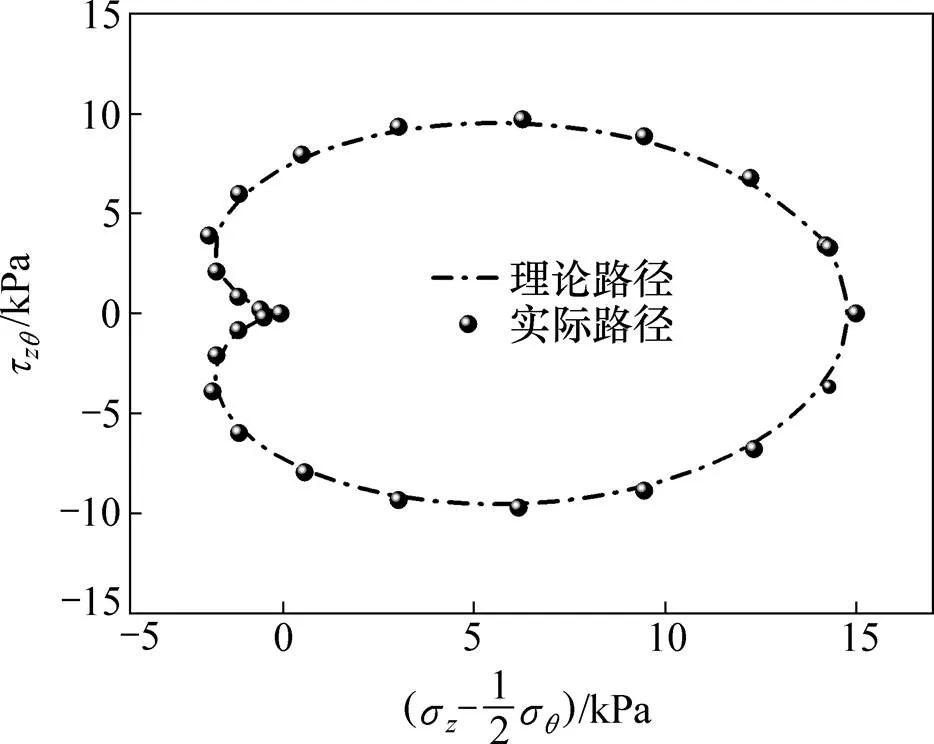
图2 试验中的实际与理论应力路径图(η=0.15)

1.3 试验结果分析

图3所示为主应力心形旋转下试样累积轴向应变与时间关系，可以将循环荷载下土体动力变形分为3种类型：稳定型、临界型与破坏型。3种类型曲线特征以应变增长率来描述，其中稳定型曲线应变增长速率一直保持逐步减小，当加载至一定次数后，试样被压密到一定程度，此时只产生弹性应变或微小塑性应变，永久应变量逐渐趋于稳定，并维持在比较小的范围内，如试样HSR10，HSR15和HSR20。

主应力心形旋转下稳定型累积应变与时间对数关系曲线如图4所示。由图4可以看出：塑性累积变形为稳定型时，当振动次数大于100时，主应力心形旋转路径下，轴向塑性累积变形与时间的对数呈良好的线性关系，可以建立如下大数目循环荷载下土体塑性累积变形经验方程：

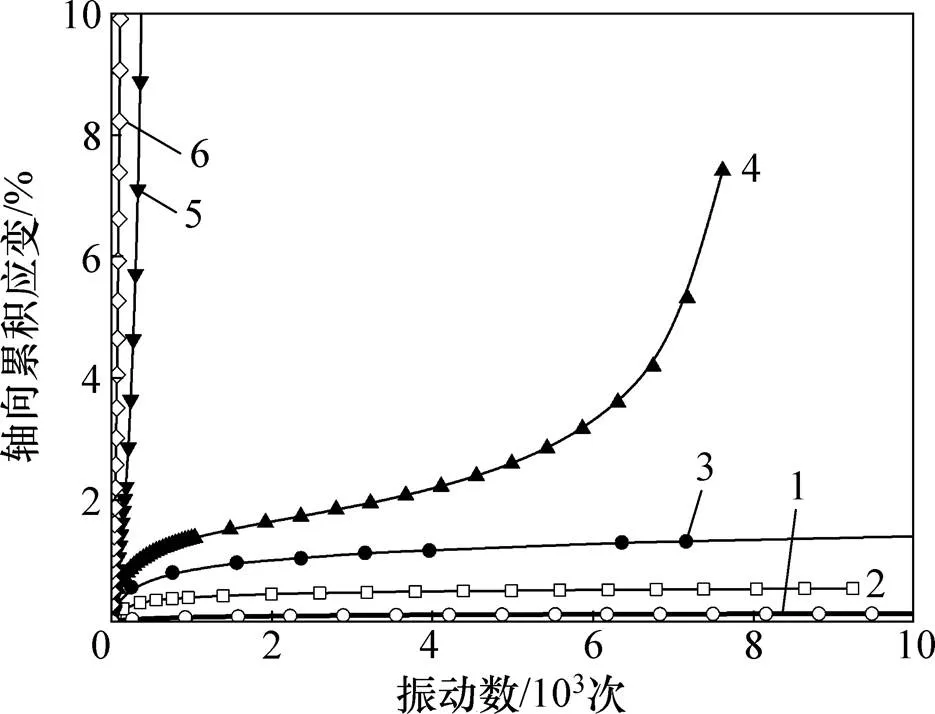
1—HSR10；2—HSR15；3—HSR20；4—HSR23；5—HSR25；6—HSR30。

图3 主应力心形旋转路径下轴向累积应变与振动次数的关系曲线

Fig. 3 Curves between axial cumulative strain and vibration times under principal stress heart-shaped rotation path

利用式(1)对不同主应力轴旋转模式下土体轴向塑性累积应变趋势进行预测，得到的计算与实测值对比见图5。

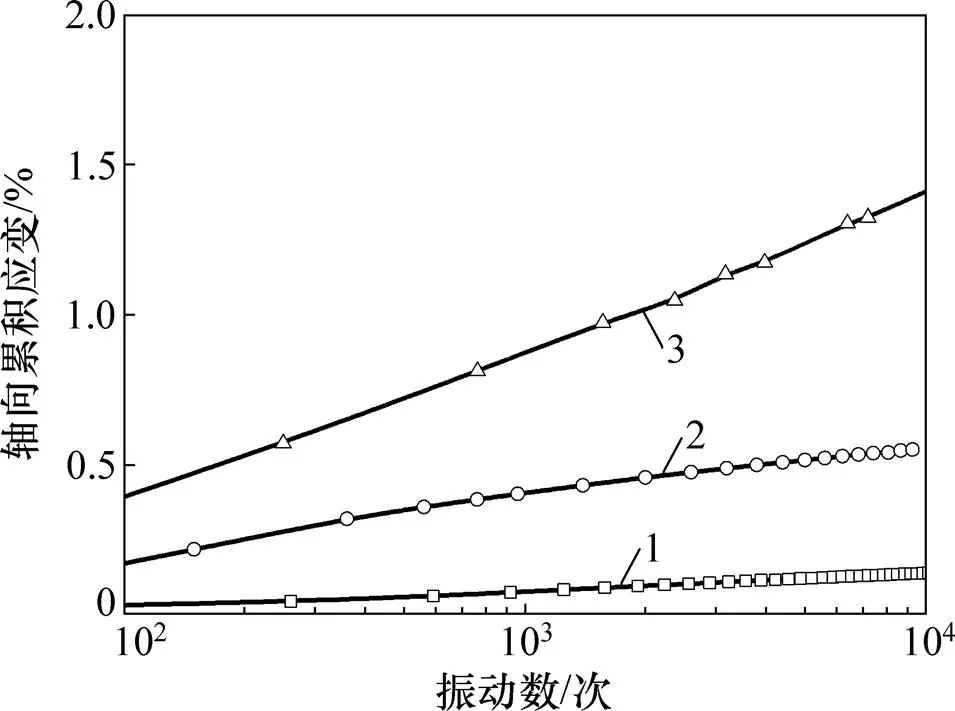
1—HSR10；2—HSR15；3—HSR20。

图4 主应力心形旋转下稳定型累积应变与时间对数关系曲线

Fig. 4 Curves between axial cumulative strain and vibration times under principal stress heart-shaped rotation path

由图5可见：式(1)亦可以很好地预测不同主应力轴旋转路径下土体的塑性累积变形，进一步可以对交通荷载下软土地基长期沉降变形开展预测，不同主应力轴旋转路径拟合的参数见表3。

如图6所示的主应力心形旋转路径下不同固结压力的土体累积变形与振动次数的关系曲线，不同固结压力下的累积变形开展曲线基本重合，故可以用初始固结压力对累积变形进行归一化处理。

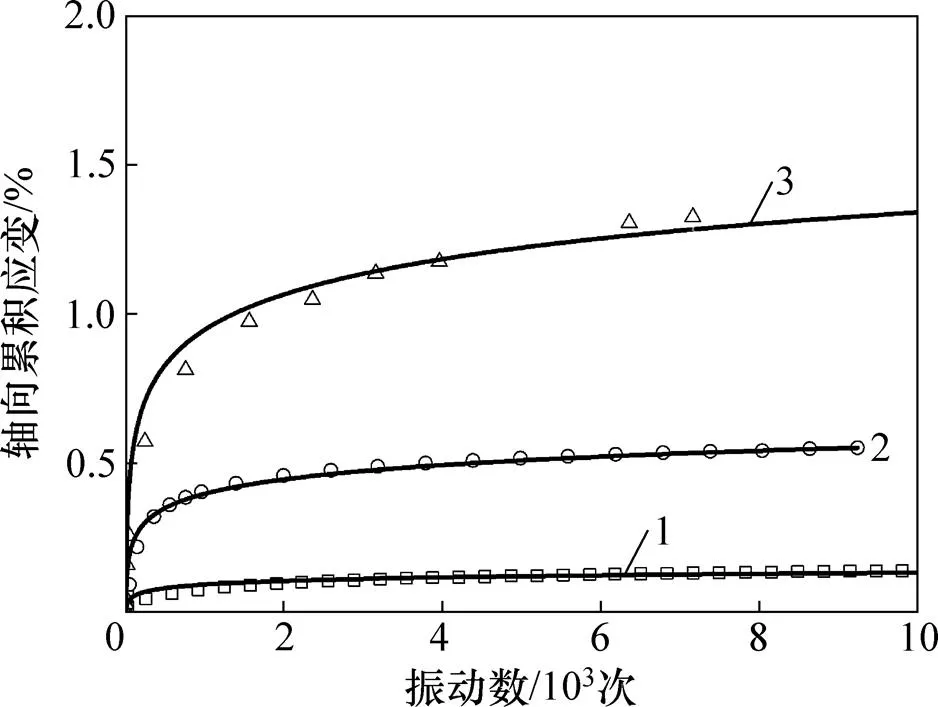
1—HSR10；2—HSR15；3—HSR20。

图5 稳定型轴向累积应变预测值与实际值对比

Fig. 5 Comparison between stable axial strain accumulation predicted values and actual values

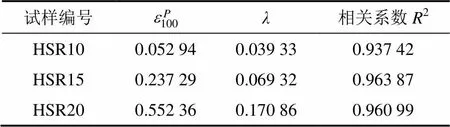
表3 轴向塑性累积应变模型拟合参数

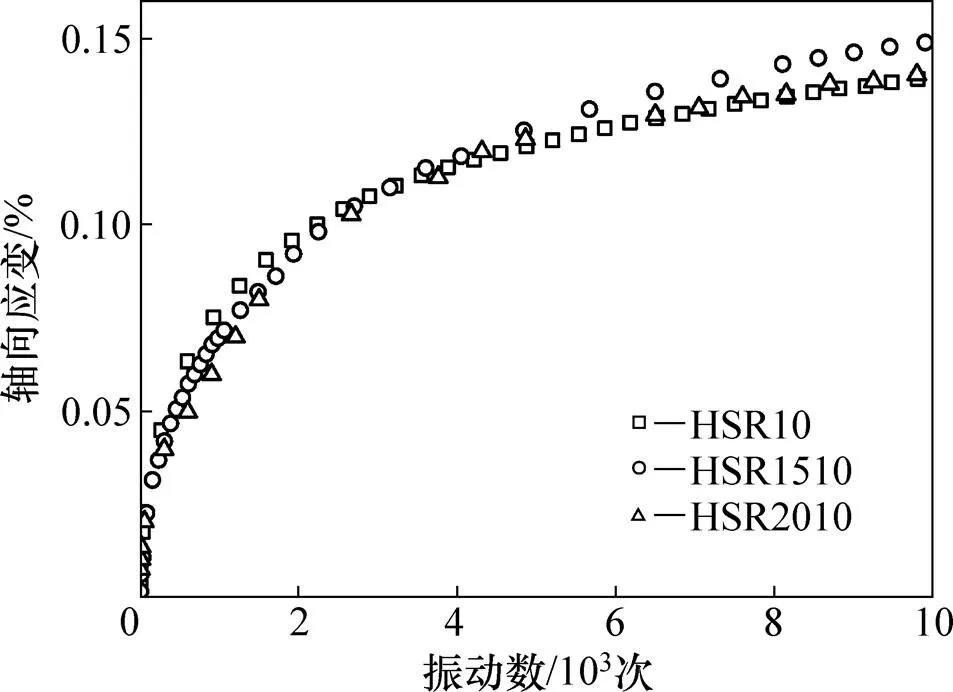
图6 主应力心形旋转路径下不同固结压力的土体轴向累积应变与振次的关系曲线

式中：1，1，1和1均为试验常数。

通过回归分析，求得式(2)和(3)中的参数分别为1=78.850 08，1=3.080 59，1=65.575 72，1=3.178 62，将这些参数代入式(2)和式(3)并联合式(1)有：

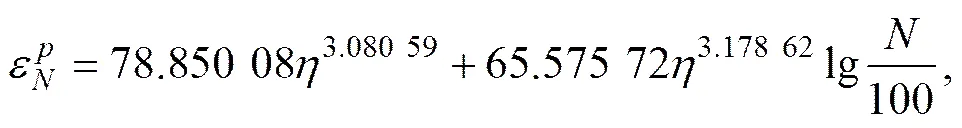
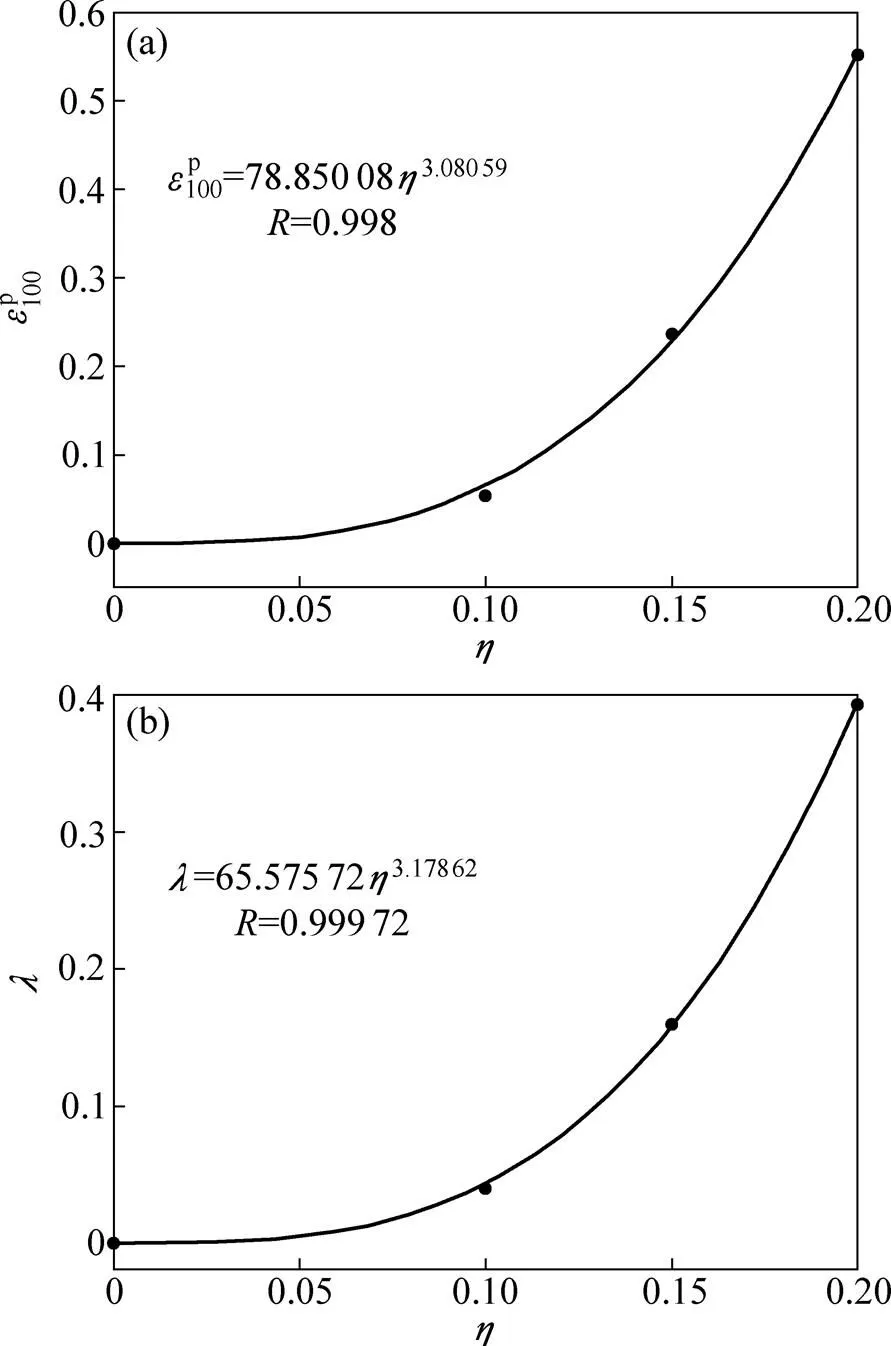
(a)；(b)−

图7 应变累积预测模型中参数和随动应力水平的变化曲线

Fig. 7 Curves between parameters,of strain prediction model and dynamic stress ratio

2 累积孔压预测模型

图8所示为主应力心形旋转下，试样累积孔压与时间关系曲线。可见：累积孔压发展趋势与试样轴向塑性累积变形发展规律类似，亦可以划分为3种类型：稳定型、临界型与破坏型。3类曲线同样以孔压增长率来描述，其中开始阶段稳定型曲线孔压增长较快，后逐渐变缓，并在振动次数达到4 000次左右时，孔压基本趋于稳定，同时达到该应力比条件下的极限孔压，如试样HSR10，HSR15和HSR20。

交通荷载的反复循环不仅会造成饱和软黏土塑性应变的不断累积，而且会造成饱和软黏土孔隙水压力的不断累积。软黏土由于渗透性较低，在短期内可以视为不排水；但交通荷载为长期荷载，随着时间的推移累积，孔隙水压力最终将消散而造成固沉降。为了计算交通荷载引发孔压消散产生的固结沉降量，需进一步分析稳定型试样的孔压开展特征，以建立相应的孔压累积模型。

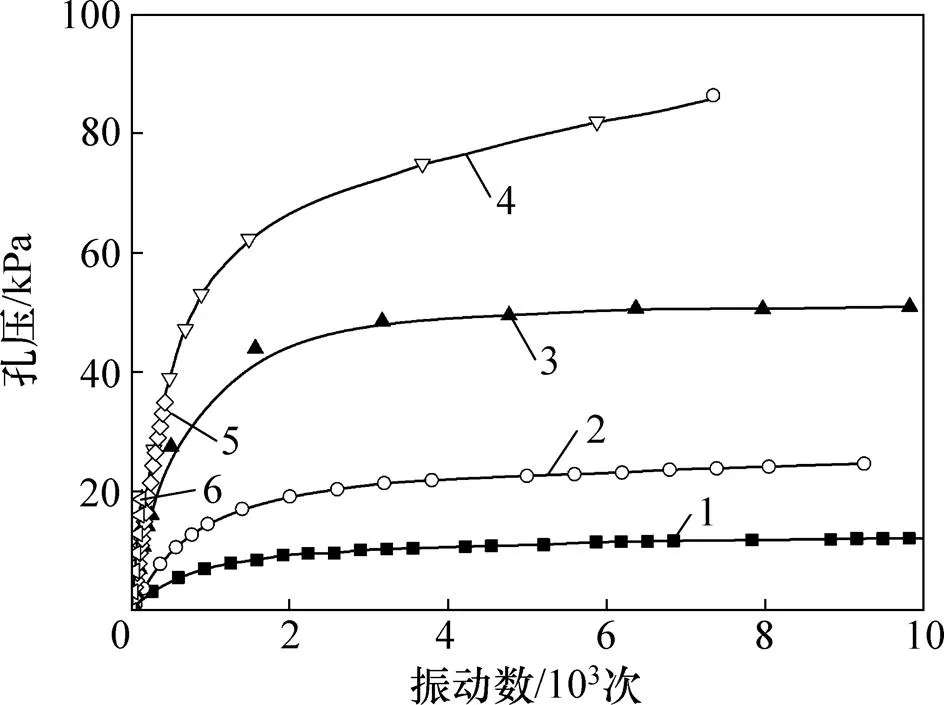
1—HSR10；2—HSR15；3—HSR20；4—HSR23；5—HSR25；6—HSR30。

图8 主应力心形旋转下累积孔压与振动次数的关系曲线

Fig. 8 Curves between cumulative pore pressure and vibration times under principal stress heart-shaped rotation path

如图9所示为主应力心形旋转路径下不同固结压力的土体孔压与振次的关系曲线。可见：不同固结压力下的累积孔压开展曲线基本重合，故可以用初始固结压力对累积孔压进行归一化处理。

在已有的孔压模型中，许多学者建立了孔压与应力、孔压与应变、孔压与能量、孔压与软化指数等一系列模型，其中应力模型主要有指数型、对数型、双曲线型、多项式型等。经过前面的分析，稳定型试样的累积孔压开展进行到后期，增长速率明显降低，趋于稳定，主应力心形旋转下重塑黏土孔压开展存在极限状态，而以上应力模型中除了双曲线型外，其他几种模型的预测孔压随着振次的增加而增加，虽后期增长速率明显降低，但仍存在一个不容忽视的增长趋势，不存在极限状态，故选定双曲线来拟合：

式中：2和2为试验参数。

为进一步验证上述分析思路，以0/为纵坐标，以振动次数为横坐标，构成新的坐标系，则双曲线变成直线如图10所示，其曲线斜率为2，截距为2。

利用式(2)对主应力心形旋转下土体累积孔压开展趋势进行预测，得到的计算与实测值对比见图11。

由图11可见：式(2)可以很好预测不同动应力水平下土体的累积孔压。相关拟合的参数见表4。

图12所示为孔压累积预测模型中2个参数随动应力水平的变化曲线，可以用下式来进行拟合：

2=2+2(6)

式中：2，2，2和2均为试验参数。

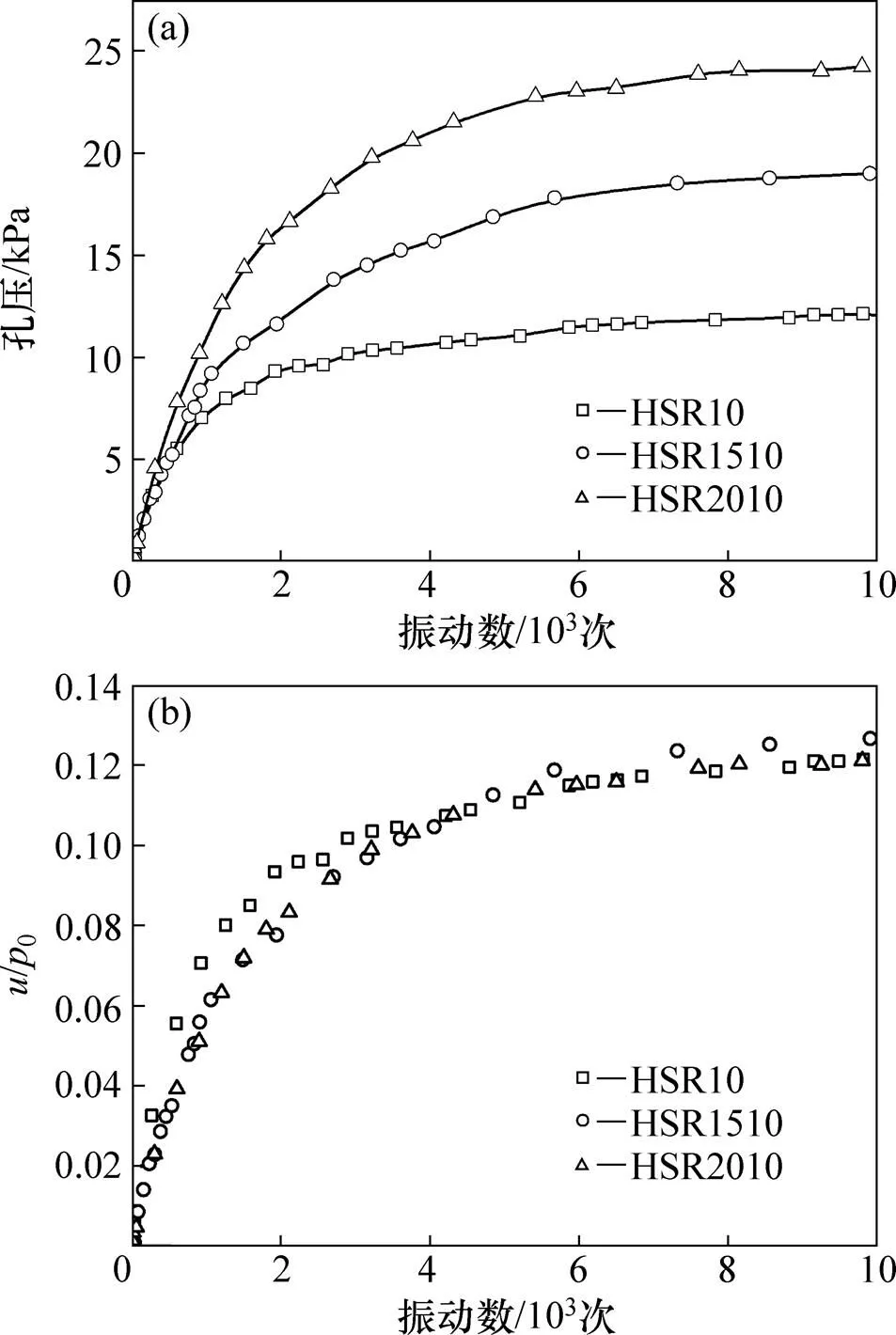
(a) 土体孔压；(b) 归一化的土体孔压

图9 主应力心形旋转路径下不同固结压力的土体孔压与振次的关系曲线

Fig. 9 Curves between pore pressure and vibration times under principal stress rotation in different consolidation pressure

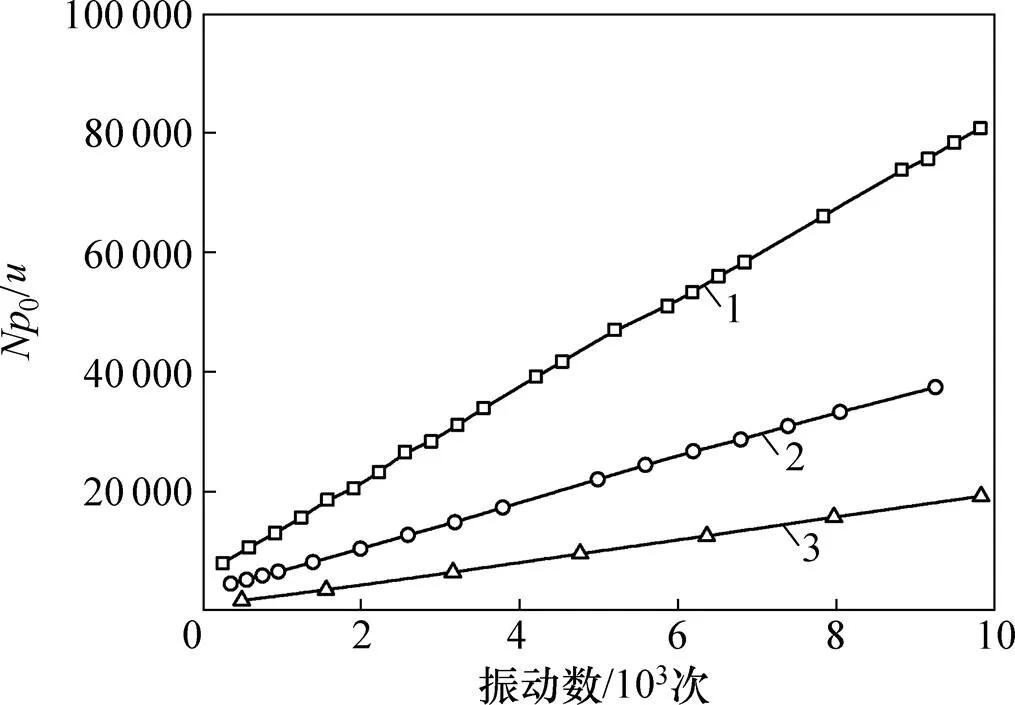
1—HSR10；2—HSR15；3—HSR20。

图10 主应力心形旋转路径下0/与振次的关系曲线

Fig. 10 Curves between0/and vibration times under principal stress heart-shaped rotation path

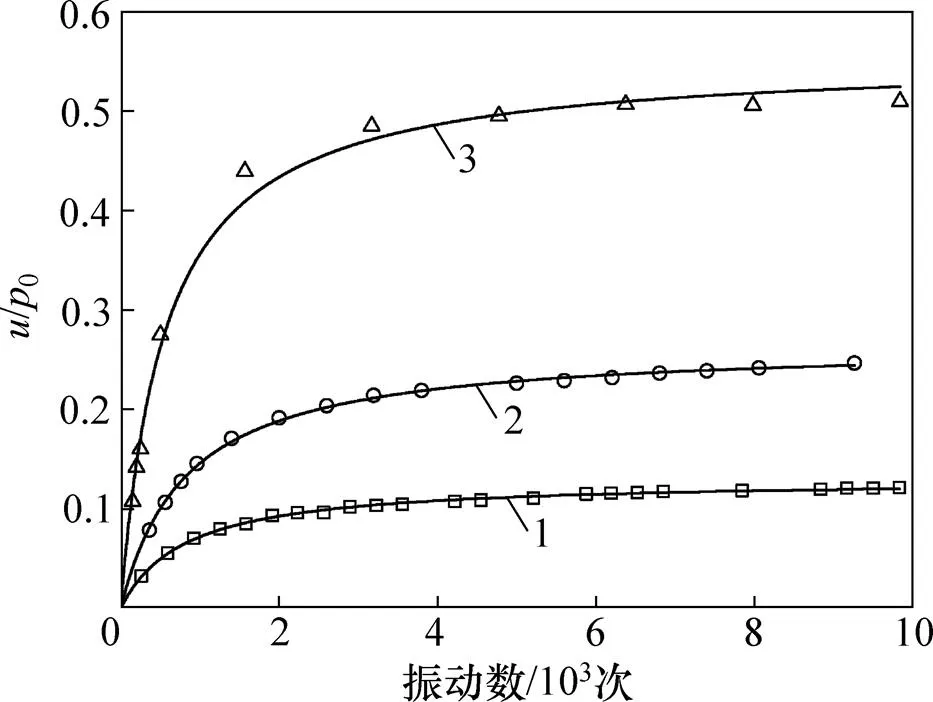
1—HSR10；2—HSR15；3—HSR20。

图11 稳定型累积孔压预测值与实际值对比

Fig. 11 Comparison between stable pore pressure accumulation predicted value and actual value

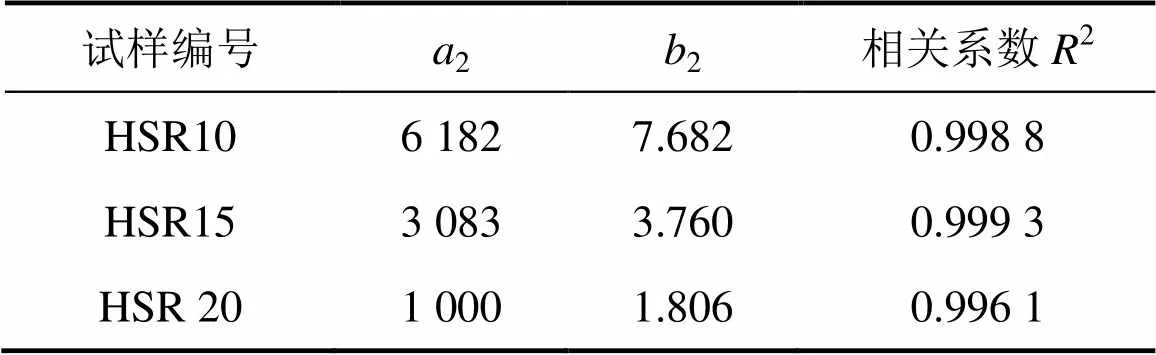
表4 稳定型累积孔压模型拟合参数表

通过回归分析，求得式(6)和(7)中的参数分别为2=11 570，2=55 040，2=0.100 3，2=−1.889，将这些参数代入式(6)和(7)并联合式(1)有

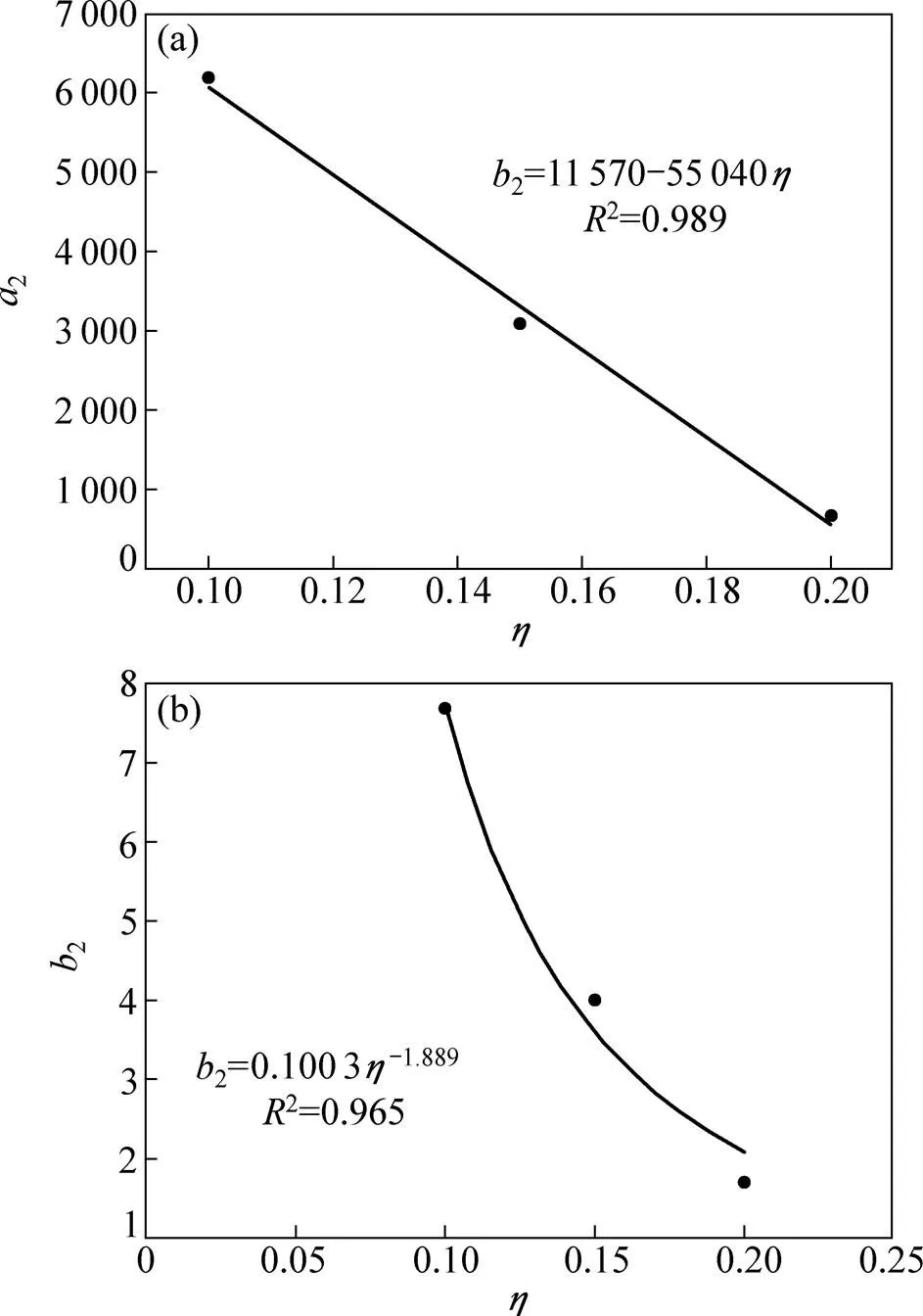
(a)2−；(b)2−

图12 孔压累积预测模型中参数随动应力比的变化曲线

Fig. 12 Curves between parameters of pore pressure prediction model with dynamic stress level

3 实例分析

3.1 数值模型及其计算参数

用Abaqus建立三维有限元模型来模拟模型试验中路基内部动土压力随路基深度的分布。有限元计算采用的是显式动力计算方法，自动时间步长。路基结构用三维有限元模型模拟，如图13所示。地基长×宽×高为30 m×30 m×20 m。所有单元采用8节点6面体缩减单元。

图13 路基三维有限元计算模型

表5 轨道系统与路基结构参数

在行业标准TB10621—2009“高速铁路设计规范(试行)”相关规定基础上，参考相关文献，决定对轨道板、CA砂浆层、底座、基床地层、机床表层及地基均采用线弹性动力本构模型，轨道系统与路基结构的参数见表5。

3.2 列车等效移动荷载的施加

不论是传统的有砟轨道，还是近年来兴起的无砟轨道，由于枕木或扣件系统存在，可把作用于轨道上的列车移动荷载化成位置固定的竖向振动荷载，从数学角度看，是把荷载从对时间−位置变化的函数变换成只是时间的函数。可以通过对不同扣件施加一定相位差的波形来模拟列车荷载的移动效应。

加载系统模拟输入荷载时程曲线如图14所示(其中，和max分别为循环轴力及其峰值)。已有的理论计算或实测结果表明[10]，单轮轴荷载下轨枕力的加载波形为“W”形；列车移动荷载下轨枕力为多个具有一定相位差的相同的波形的叠加耦合，为“M”形，2个波峰则对应着1个转向架的2组轮轴。该波的波长与单轮轴荷载下轨枕力的加载波长相同，相同速度下的频率也相同，不同的是具体的波形与幅值。

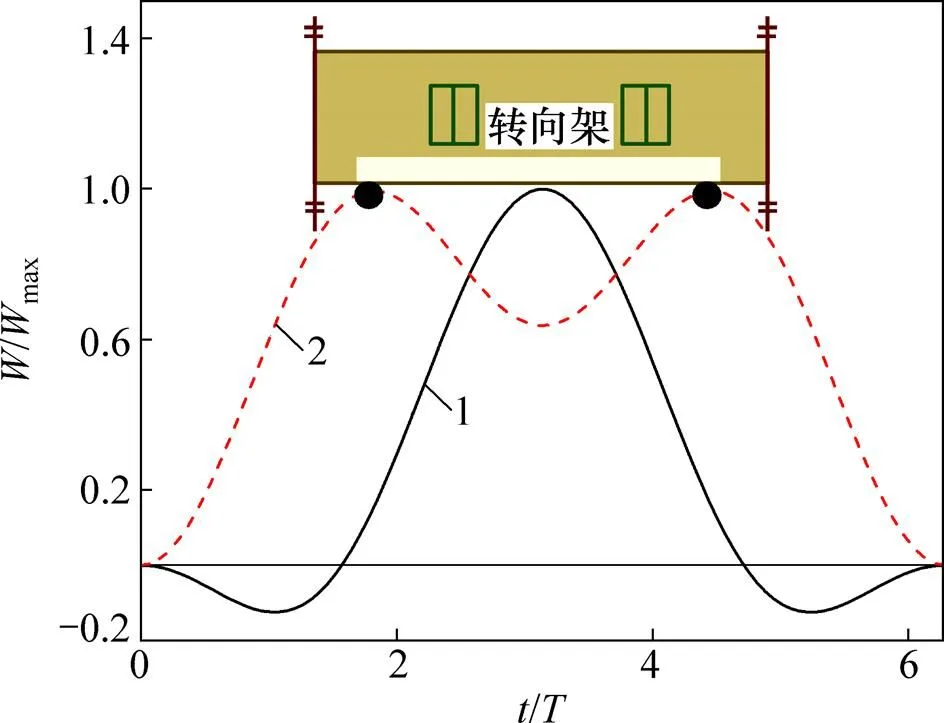
1—单轴荷载；2—列车荷载。

图14 加载系统模拟输入荷载时程曲线

Fig. 14 Duration curves of loading system load

分布式的加载系统通过改变加载波的频率与相位差来模拟列车的不同运行速度。在确定加载波的频率之前首先要确定加载波的波长。胡一峰等[11]给出了基于实测结果建议的扰动波长度，对于无砟轨道，当路基深度距轨顶距离小于3.0 m时，取扰动波长为固定轴距2.5~3.0 m到转向架的间距7.0 m。这里以轮轴定距在波长中占据的比例反推出波长为6.3 m，扣件数为11，相邻轨枕间的距离为=0.63 m，列车时速，加载波的频率，相邻轨枕的加载时间间隔0，相位差用表示，则

分布式加载系统对列车时速的模拟控制如表6所示。

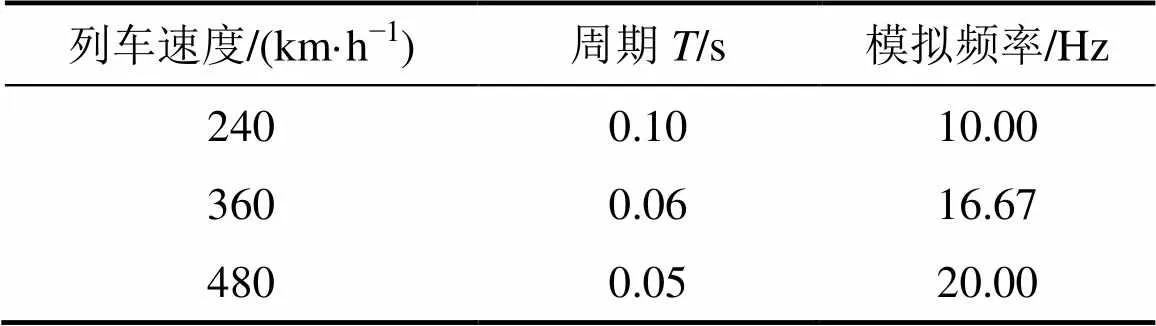
表6 列车速度与加载波形的周期、频率的关系

德国铁路设计规范[12]中规定动力荷载放大系数的计算为

式中：为曲线荷载系数，主要用于考虑曲线地段轮重荷载重分布产生的附加影响，一般取1.1~1.2；为轨道状态系数，用于考虑轨道上部结构状态对动力荷载的影响，包括磨损、约束和轨道变形等。在一般情况下，高速铁路由于建设标准高、维护质量好，取值为0.15；为统计安全度系数，对于轨道上部结构，其失效可能给系统带来十分严重的后果，对应的安全系数取=3；考虑行车速度对动力荷载的影响，采用以下经验公式取值：

本文对轨枕的动力荷载放大系数的计算参照德国铁路方法。数值模型中线路属于直线地段，故取=1。模型参数的选取严格依据高速铁路的标准，故=0.15。对于轨枕结构，=3。

数值模型中模拟的车型CRH3型，轴质量为17 t，钢轨型号为CHN60，轨枕接触面积=0.045 m2，转向架上2个轴的质量由11个轨枕承担，设每个轨枕上施加的最大应力为max，单位波长范围内每个轨枕承担的应力P与最大应力max的比值设为x，则有

经过计算，列车速度与动力放大系数、数值模型加载应力的关系如表7所示。

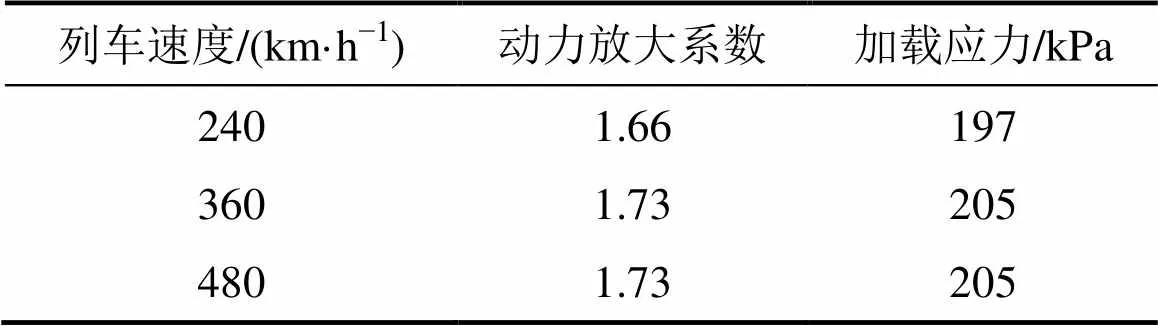
表7 列车速度与动力放大系数、数值模型加载应力的关系

3.3 动应力水平分析

由前面的理论研究发现：土体的动应力比是影响地基沉降变形最关键的因素。不同深度处的动应力比如图15所示。从图15可见：随着深度的不断增加，土体的动应力比也逐渐减小，这种衰减趋势并非呈线性变化，而是在靠近地面处，土体的动应力比衰减剧烈；当深度超过6 m后，土体的动应力比在0.01以下，且逐渐趋于稳定。此外，当速度由240 km/h提升至360 km/h后，在2 m深度以内土体的动应力水平变大，但2 m以下土体的动应力比反而减小；而当速度由360 km/h提升至480 km/h后，整个地基深度范围内土体的动应力水平都有所减小，在1 m深度以内的土体动应力水平比240 km/h速度时土体的动应力水平高，在1 m深度以下则正好相反。

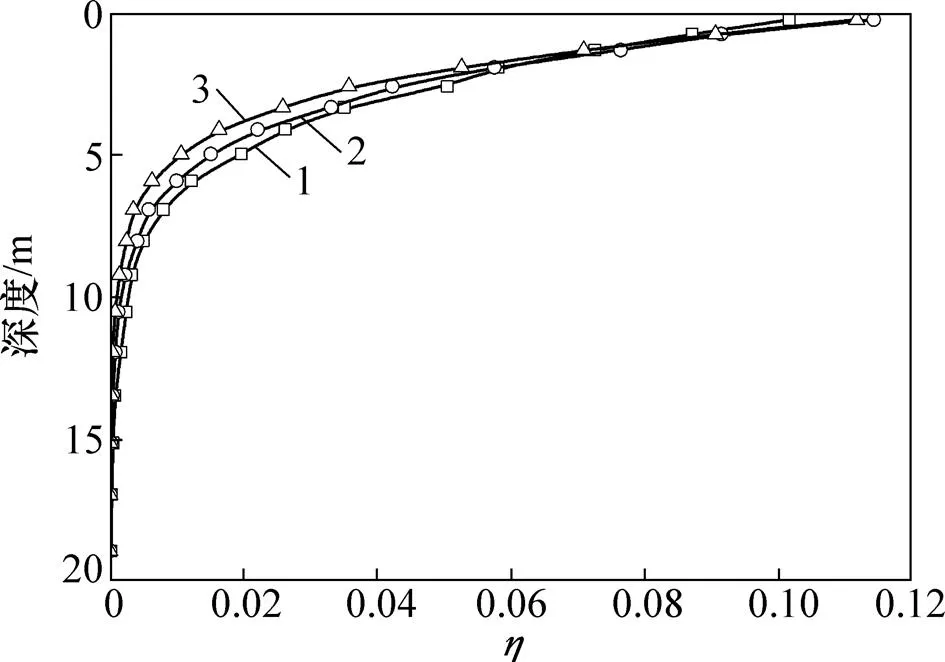
/(km∙h−1)：1—240；2—360；3—480。

图15 动应力比随深度的变化曲线

Fig. 15 Relationship between dynamic stress ratio and depth

3.4 长期沉降计算分析

3.4.1 不排水累积变形计算

不排水条件下土体变形1为

式中：i为各层土的厚度；为分层总数；ε为各层土的不排水累积应变，可以采用式(4)计算。

3.4.2 排水固结累积变形计算

根据路堤下软土地基分层应力状态得到每层中心点孔隙水压力，代替该层孔压。孔隙水压力消散过程可采用太沙基一维固结理论计算，每层固结沉降由该土层对应固结度控制，将各层固结变形相加后可得整体土层固结沉降2：

式中：i为第层不排水循环累积孔压；m为第层体积压缩系数，本文中土体的体积压缩系数为2.5 MPa；U为第层固结度，不排水循环累积孔压一般不会很快消散，但从长期效应来说，可以认为累积孔压已经完全消散，即U=100%，这样的估算在工程中是偏保守的。每层土累积孔压采用本文提出循环累积孔压模型计算。

3.4.3 总沉降变形分析

不同速度下地基的总沉降与振动次数的变化关系如图16所示。每节车厢2个转向架，每个转向架经过在土体中产生1次振动，京沪高铁日开172列火车，假定每列火车20节车厢，则1 a中土体要经受约250万次振动。随着振动次数的不断增加，总沉降量逐渐增大，但其增大速率迅速减小，当振次超过250万次时出现拐点，总沉降速率不断趋于稳定。以速度360 km/h为例，1 a后地基的总沉降为8.78 mm，而此后 3 a的沉降量仅为0.44 mm，增至9.22 mm。第1年的沉降量占4 a总沉降量的95.3%。

地基的总沉降量与列车的运行速度没有明显的比例关系，当运行速度为360 km/h时，地基总沉降量最大；运行速度为480 km/h时，地基总沉降量最小；当振次为1 000万次时，速度由240 km/h提升至360 km/h后，沉降量由8.51 mm增大至9.22 mm，增大了约8.3%。与前面的应力分布相对应，当速度由360 km/h提升至480 km/h后，地基的总沉降量减小至7.97 mm，减小了约13.6%。

不同速度下地基的总沉降与深度的变化关系如图17所示。从图17可以看出：随着深度不断增加，土体总沉降量也不断减小，整体沉降主要发生在约5m以上部分。以速度360 km/h为例，该部分沉降量为9.02 mm，为总沉降量9.22 mm的97.8%，距地面5 m处的动应力比为0.015，说明当动应力比小于0.015时，地基土层产生的沉降量很小。在整个深度范围内，速度480 km/h下的土层沉降量最小，与前面分析的动应力相对应；在深度2 m以下，速度240 km/h下土层的沉降量大于速度360 km/h下的土层沉降量。

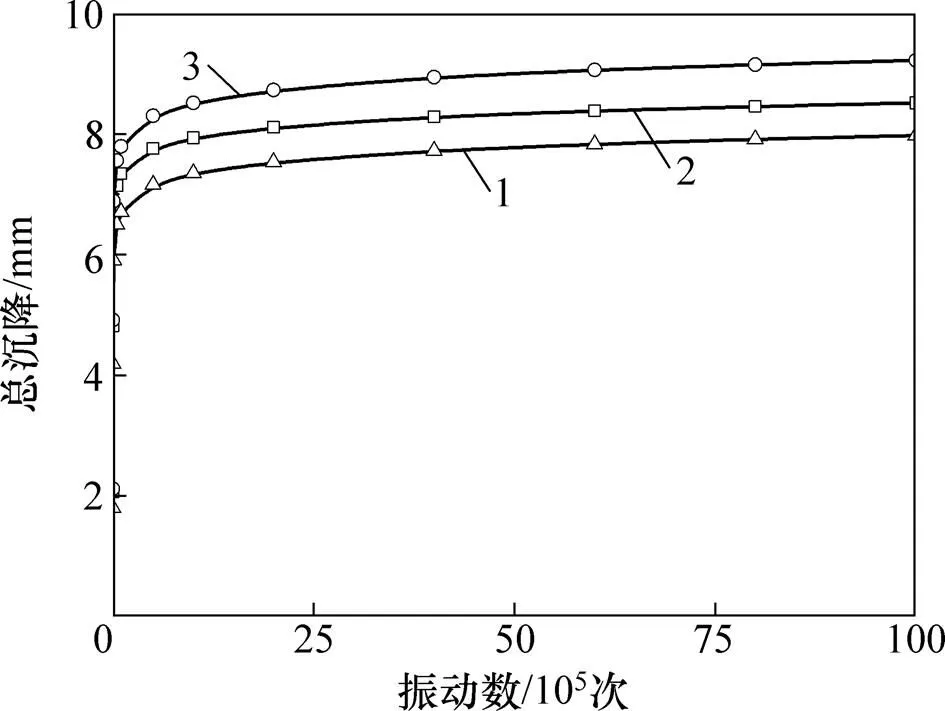
运行速度/(km∙h−1)：1—240；2—360；3—480。

图16 地基总沉降随振动次数的变化曲线图

Fig. 16 Relationship graph of ground total settlement with vibration times

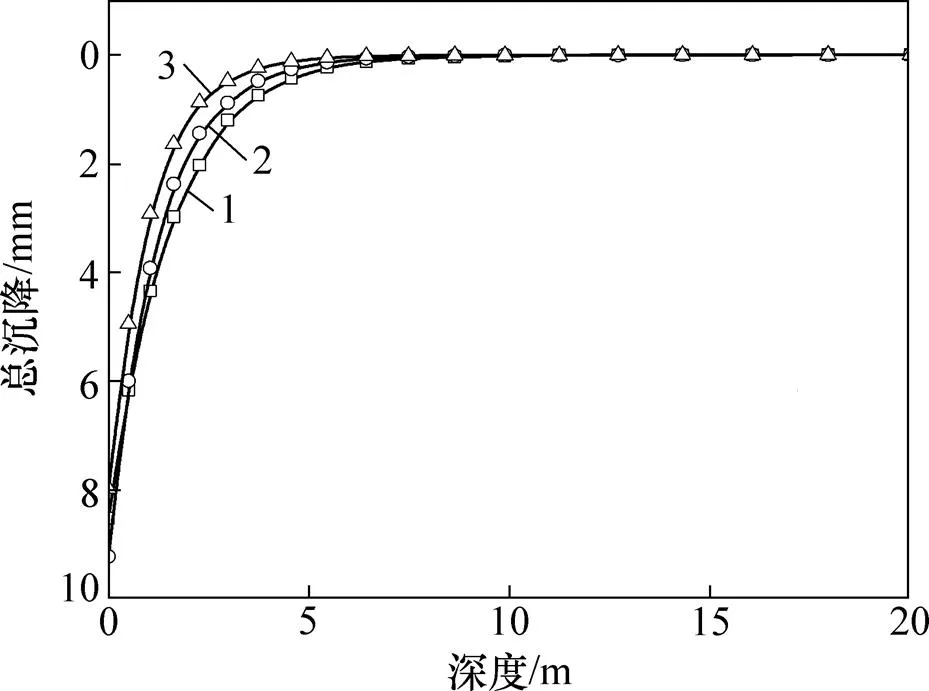
列车运行速度/(km∙h−1)：1—240；2—360；3—480。

图17 地基总沉降随深度的变化曲线

Fig. 17 Relationship between ground total settlement and depth

4 结论

1) 交通荷载引发主应力轴旋转下土体不排水累积变形和累积孔压可以用围压进行归一化，并以此建立相应的经验预测模型，进一步确定模型参数表达式。

2) 在有限元数值计算中引入等效移动列车荷载，使得数值计算中土体的应力状态更符合工程实际情况。随着深度的增加，土体的动应力比也逐渐减小，这种衰减趋势并非呈线性变化，而是在靠近地面处，土体的动应力比衰减剧烈；当深度超过6 m后，土体的动应力比在0.01以下，且逐渐趋于稳定。

3) 建立高速列车荷载作用下地基软土的累积变形计算方法，研究交通荷载下地基软土的长期变形沉降规律，为沉降控制提供了一种合理的评价方法。随着振动次数的不断增加，总沉降量逐渐增大，但其增大速率迅速减小；当振次超过250万次时出现拐点，总沉降速率不断趋于稳定，第1年的沉降量占4 a总沉降量的90%以上；随着深度的不断增加，土体总沉降量也不断减小，整体沉降主要发生在距地面5 m以上部分，该部分的沉降量占总沉降量的95%以上；随着列车运行速度增大，地基土层的总沉降增大，但当列车速度超过临界速度时，地基的总沉降量反而大幅度减小。

[1] 陈基炜, 詹龙喜. 上海市地铁一号线隧道变形测量及规律分析[J]. 上海地质, 2000(2): 51−56. CHEN Jiwei, ZHAN Longxi. Deformation measuring of the metro tunnel and deformation data analysis of Shanghai Metro Line No.1[J]. Shanghai Geology, 2000(2): 51−56.

[2] CHEN Y M, WANG C J, CHEN Y P, et al. Characteristics of stresses and settlement of ground induced by train[C]// Environmental Vibration Prediction, Monitoring and Evaluation. London: Taylor & Francis/Balkema, 2005: 33−42.

[3] GRABE P J, CLAYTON C R I. Effects of principal stress rotation on accumulative deformation in rail track foundations[J]. Journal of Geotechnical and Geo-environmental Engineering, 2009, 135(4): 555−565.

[4] 钱建固, 王永刚, 张甲峰, 等. 交通动载下饱和软黏土累计变形的不排水循环扭剪试验[J]. 岩土工程学报, 2013, 35(10): 1790−1798. QIAN Jiangu, WANG Yonggang, ZHANG Jiafeng, et al. Undrained cyclic torsion shear tests on permanent deformation responses of soft saturated clay to traffic loadings[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1790−1798.

[5] 肖军华, 许世芹, 韦凯, 等. 主应力轴旋转对地铁荷载作用下软黏土累积变形的影响[J]. 岩土力学, 2013, 34(10): 2938−2944. XIAO Junhua, XU Shiqin, WEI Kai, et al. Influences of rotation of principal stress axis on accumulative deformation of soft clay under subway cyclic loading[J]. Rock and Soil Mechanics, 2013, 34(10): 2938−2944.

[6] 陶明安, 沈扬, 王鑫, 等. 空心圆柱仪模拟列车荷载下土中应力路径能力分析[J]. 岩土力学, 2013, 34(11): 3166−3172. TAO Ming’an，SHEN Yang，WANG Xin, et al. Ability analysis of HCA to imitate stress path of soil caused by train load[J]. Rock and Soil Mechanics, 2013, 34(11): 3166−3172.

[7] 沈扬, 陶明安, 王鑫, 等. 交通荷载引发主应力轴旋转下软黏土变形与强度特性试验研究[J]. 岩土力学, 2016, 37(6): 1569−1578. SHEN Yang, TAO Ming’an, WANG Xin, et al. The experimental study of deformation and strength characteristics on soft clay under principal stress axis rotation caused by traffic load[J]. Rock and Soil Mechanics, 2016, 37(6): 1569−1578.

[8] 姚兆明, 张明慧, 陈军浩. 饱和软黏土循环累积孔压模型及地铁隧道路基长期沉降计算[J]. 铁道学报, 2012, 34(9): 1157−1163. YAO Zhaoming, ZHANG Minghui, CHEN Junhao.Cyclic accumulative pore pressure explicit model of saturated soft clay and long-term settlement calculation of subway tunnel roadbed[J].Journal of the China railway Society, 2012, 34(9): 1157−1163.

[9] 蔡袁强, 刘新峰, 郭林, 等. 飞机荷载作用下超载预压软土地基的长期沉降[J]. 浙江大学学报(工学版), 2013, 47(7): 1157−1163. CAI Yuanqiang, LIU Xinfeng, GUO Lin, et al.Long-term settlement of surcharge preloading foundation in soft clay area induced by aircraft loads[J].Journal of Zhejiang University (Engineering Science), 2013, 47(7): 1157−1163.

[10] 边学成, 蒋红光, 金皖锋, 等. 板式轨道–路基相互作用及荷载传递规律的物理模型试验研究[J]. 岩土工程学报, 2012, 34(8): 1488−1495. BIAN Xuecheng, JIANG Hongguang, JIN Wanfeng, et al. Full-scale model tests on slab track-subgrade interaction and load transfer in track system[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1488−1495.

[11] 胡一峰, 李怒放. 高速铁路无砟轨道路基设计原理[M]. 北京: 中国铁道出版社, 2010: 56−57. HU Yifeng, LI Nufang. Theory of ballastless track-subgrade for high speed railway[M]. Beijing: China Railway Publishing House, 2010: 56−57.

[12] Germany Railway Standard Ril836, Erdbauwerke planen, bauenund instand halten[S].

(编辑 赵俊)

Long-term settlement calculation of saturated soft clay foundation under train moving loads

TAO Mingan1, 2, SHEN Yang1, WANG Xin1, WANG Baoguang1, DU Wenhan1

(1. Key Laboratory of Geomechanics and Embankment Engineering of Ministry of Education,Hohai University, Nanjing 210098, China;2. The Third Railway Survey and Design Institute Group Corporation, Tianjin 300142, China)

The hollow cylinder apparatus was utilized to simulate the heart-shaped line path in the maximum shear stress pace. The cumulative model of strain and pore water pressure were established for saturated soft clay under train load. The equivalent moving train load was introduced to obtain the distribution of soil dynamic stress levels in dynamic FEM. Combined with the layer-wise summation method, the method of calculating soft clay foundation settlement was established under the high-speed train moving loads. The results show that with the increase of the cycles, the total settlement increases gradually while the rate decreases rapidly. The inflection point occurs when the number of cycles exceeds 2.5 million. In addition, the rate of total settlement tends to be stable while the settlement of the first year exceeds 90% of the total settlement. The total settlement of soil decreases with the increase of depth; the whole settlement mainly occurs within 5 m below the ground while the settlement occupies more than 95% of the total settlement. With the increase of train speed, the total settlement of foundation soil is not always increased. The total settlement will decrease when speed exceeds the critical value.

train; moving loads; the heart-shaped rotation of principal stress axis; cumulative plasticity model; pore pressure model; long-term settlement

10.11817/j.issn.1672-7207.2016.12.032

TU43

A

1672−7207(2016)12−4206−10

2015−12−07；

2016−03−15

国家自然科学基金资助项目(51479060，U1134207)；中央高校基本科研业务费专项资金资助项目(B15020060) (Projects(51479060, U1134207) supported by the National Natural Science Foundation of China; Project(B15020060) supported by the Fundamental Research Funds for the Central Universities)

沈扬，博士，教授，从事土体静动力学特性和本构理论研究；E-mail：shenyang1998@163.com