硅基半导体多场耦合下的光传输及电调控特性分析
周 吉, 贺志宏, 于孝军, 杨东来, 董士奎
(1. 哈尔滨工业大学 能源学院, 黑龙江 哈尔滨 150001; 2. 中国空间技术研究院第508研究所, 北京 100094; 3. 中国科学院 长春光学精密机械与物理研究所, 吉林 长春 130033)
硅基半导体多场耦合下的光传输及电调控特性分析
周 吉1,2, 贺志宏1*, 于孝军3, 杨东来3, 董士奎1
(1. 哈尔滨工业大学 能源学院, 黑龙江 哈尔滨 150001; 2. 中国空间技术研究院第508研究所, 北京 100094; 3. 中国科学院 长春光学精密机械与物理研究所, 吉林 长春 130033)
针对硅基半导体电光热多场耦合特性及电调控问题,引入泊松方程和载流子连续性方程来计算载流子输运过程的浓度分布,利用德鲁德-洛伦兹公式和K-K关系式考虑载流子浓度变化对于光折射率和吸收系数的影响,并根据电磁耗散求解热沉积项。通过对半导体基本方程、电磁波动方程和能量方程的耦合方程组进行有限元求解,模拟并分析了电光热三者耦合作用下硅基半导体介电属性及光传输行为随外加电压、载流子初始浓度、换热系数等影响因素的变化规律。研究指出了半导体P区表面反射光电场模随外加电压的降低而升高,随换热系数的增大而降低的规律。利用该机制给出了对反射光强空间分布进行电热调控的方案。
硅基半导体; 载流子浓度; 热光效应; 电光效应; 电热调控
1 引 言
硅基电光调制在滤波器、调制器、复用/解复用器、可重构光插分复用器、波长转换器、光开关等光电器件中有着广泛的应用。由于硅具有易集成、低成本以及大容量等特点,近年来已经逐渐取代铌酸锂(LiNbO3)成为制造电光器件的主要材料。已有研究证明,温度是影响光束传输质量的一个重要因素[1-2]。而硅电光调制器作为光传输的一种主要媒介,随着对其大容量传输和精确传输要求的提高,温度对电光调制的稳定性和精确度的影响也日益受到重视。文献[1]中指出,如果温度上升6 ℃,硅折射率变化为1.1×10-3,这个变化已经可以与等离子体色散引起的电光效应相比较。
早在1990年,Oheda[3]就研究了掺杂非晶硅薄膜中由于外加电场的调制作用导致的光吸收因子的改变。2007年,Liu等[4]设计了一种基于自由载流子等离子体耗散效应制作的高速和高规格的硅基光调制器。2012年,Rao[5]展示了沉积温度低至190 ℃的低损耗氢化非晶硅波导中快速光诱导的吸收效果。王兴军[6]针对一种新型的硅基发光材料——铒镱/钇酸盐化合物开展了一系列基础研究,研制出了基于该物质的电致发光器件,并从理论上证明了这种材料实现电泵浦激光的可行性。朱景程[7]研究了电场和应力诱导的场致线性电光效应。根据硅材料中各种电光效应具有不同的偏振依赖特性和电场响应特性,讨论了近本征硅样品中的场致线性电光效应、克尔效应、等离子色散效应、热光效应等对电光信号的贡献,证实了场致线性电光效应是非常显著的电光效应。2013年,Gao等[8]报道了一个GHz速度的采用非晶硅波导来强烈地限制光的铌酸锂调制器,并指出这种新的硅基-铌酸锂平台将使多种器件和电路能用于光子射频、非线性光学和量子光学领域。Chmielak[9]详细研究了包覆碳化硅应变层的应变硅波导内的局部应变分布和诱导的二阶光学非线性电光效应。2014年,Noborisaka等[10]研究了超薄绝缘体硅栅金属氧化物半导体发光二极管直接/间接带中光传输的电调制,研究结果有助于促进互补MOS(CMOS)-兼容硅光子器件和新兴基于控制谷自由度的能谷电子的发展。
以上研究多集中在电光效应本身,很少有考虑电场和温度的共同作用,尤其是对半导体电场作用下电光热多场耦合机制及光响应特性尚缺少充分的研究,对于如何利用电光效应来调控热光效应机制、方法的研究也尚未见诸报道。而针对上述问题的研究有助于了解半导体多场耦合作用机制,同时也有助于在考虑温度效应的条件下对光路的精确调节及为温度负补偿还原真实光路技术提供参考。鉴于此,本文开展了在高斯激光入射下,考虑电光热耦合作用下的半导体属性变化及光传输行为的研究。
本文采用有限元方法来求解泊松方程、载流子输运方程、电磁波动方程和能量方程的耦合方程组,对多场作用下半导体的物性变化和光传输过程展开了讨论,研究了不同影响因素下硅基半导体中的载流子浓度分布、温度分布和电场模分布情况。通过比较不同电压和热边界条件下接收屏上的电场分布情况,提出了一种通过电光效应来调节热光效应的新方法。本文的研究有助于拓展采用硅基半导体制备的各种光学器件在不同热环境中的应用。
2 研究方法
本文采取电磁波频域方程来求解入射高斯激光在全场的分布,包括光在半导体表面的透反射及介质中的传输情况:
(1)
其中因变量是电场E,k0是波矢量,μr是介质的磁导率,σ是电导率,ε0是真空介电系数,ω为角频率。
光在吸收介质中传输时不可避免会存在损耗。本文主要考虑电磁能量的损耗,将损耗的能量转化为一个热源导入热传输模型中,它主要由以下两部分组成:
Qc=Qrh+Qml,
(2)
其中第一项为电阻损耗,通过方程(3)计算获得:
(3)
而第二项为磁性损耗,通过方程(4)计算获得:
(4)
半导体中的温度分布通过求解能量方程(5)和边界条件(6)获得:
(5)
-n·(-kT)=h·(Tamb-T)=q,
(6)
其中Q为内热源,q为对环境释放的热量,Tamb为环境温度,k为热导率,cp为比热。半导体中载流子浓度分布主要通过以下方程计算[11]:
-·(ε
(7)

(8)

(9)
以上3个方程用于求解半导体的物理性质,尤其是半导体内的载流子浓度关系。方程(7)又叫泊松方程,主要计算半导体里面电势的大小,其中ε为介电常数,V为电势的因变量,q是电荷,p、n分别是空穴和电子浓度,ND和NA分别为掺杂的离子浓度(ND是施主,NA是受主)。方程(8)、(9)为通过守恒定律得来的连续性方程,其中Un和Up为电子和空穴复合速率(恢复平衡的项);Jn和Jp分别为电子电流和空穴电流,通过漂移扩散方程(10)、(11)来进行计算。若考虑温度不均匀性的影响,则电子迁移率和空穴迁移率的计算公式如下[12-13]:
Jn=nμnEc+μnkBTT,
(10)
Jp=nμpEv+μpkBTT,
(11)
其中第一项叫漂移项,主要和电场梯度相关。漂移扩散方程与泊松方程之间是强耦合,相互影响。第二项叫扩散项,μn和μp分别为电子迁移率和空穴迁移率。扩散不仅和浓度梯度相关,且与温度相关。kB是波尔兹曼常数。第三项为温度的扩散项。若材料等温可以忽略掉此项。而由于本文中考虑了温度梯度,因此该项不可忽略。
在电子和空穴复合关系中,考虑硅基半导体最常见的Shockley-Reed-Hall(SRH)复合,在考虑边界接触时,采用理想欧姆接触边界条件。根据文献[1]中的报道,折射率和吸收系数随自由载流子浓度的变化关系满足以下公式:
(12)
(13)
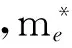
文献[1]中给出了在1.55 μm波长处的折射率、吸收系数变化值与自由载流子浓度之间的关系。通过对文献[1]中的结果推导可得,在波长0.38 μm处,硅的折射率及吸收系数变化与自由载流子浓度之间存在以下关系:
Δn=Δne+Δnh=-0.52892×10-22ΔNe-
0.51088×10-18(ΔNh)0.8,
(14)
Δα=Δαe+Δαh=0.51088×10-18ΔNe+
0.36062×10-18ΔNh.
(15)
此外文献[1]还指出,在硅基电光效应中,等离子体色散效应是最显著的电光效应。因此,本文只考虑等离子体色散这一种电光效应。
3 模型建立与求解
建立如图1所示的物理模型,入射光束为高斯光束,其传输方向垂直于光轴方向(Z轴方向)。偏振方向与入射方向垂直,且与Z轴成45°夹角。边界条件设置如图中标注所示。图中为x-y截面,横轴为x轴,纵轴为y轴,其中区域①和②为空气。区域③为硅基PN结的N区,主要导电粒子为自由电子。区域④为PN结的P区,其主要导电粒子为空穴。⑤和⑥分别为电源正负极,定义当⑤电势高于⑥时为正接,当⑤电势低于⑥时为反接。⑦为一虚拟的接收屏,距离晶体的垂直距离为1.5 μm,宽度为1 μm,用于接收投射到其上的光强信号。⑧为完美半导体边界,即电场垂直于边界界面。⑨为入射光中心点与半导体P区表面的交点,用于记录不同工况下该点处折射率和吸收系数的变化。本文中模拟基于以下假设:在复合机制上,由于光没有直接投射到复合界面上,不考虑外界光照对载流子复合速率的直接影响,只考虑光吸收热沉积引起的温度变化对复合速率的影响。载流子的复合方式只考虑SRH这一种复合方式,不考虑由于表面结构缺陷引起的晶格复合以及光生载流子复合等其他复合方式。假定PN结与电极的接触为理想欧姆接触。
本文中的初始条件设置如下:半导体施主掺杂浓度为2×1017/cm3,受主掺杂浓度为1×1017/cm3,背景施主掺杂密度为1×1015/cm3。根据硅的材料属性[14]可知,通常其相对介电常数为11.7,SRH复合时其电子寿命和空穴寿命均为10 μs,带隙为1.12 V,电子亲和性为4.05 V,价带的状态等效密度为(T/300)1.5×1.04×1019/cm3,导带的状态等效密度为(T/300)1.5×2.8×1019/cm3,电子迁移率是1 450 cm2/(V·s),空穴迁移率是500 cm2/(V·s),导热系数是131 W/(m·K),常压比热容是700 J/(kg·K),0.38 μm波长处的n、k值分别为3.268 4和0.822 6。

图1 模型框图和边界条件
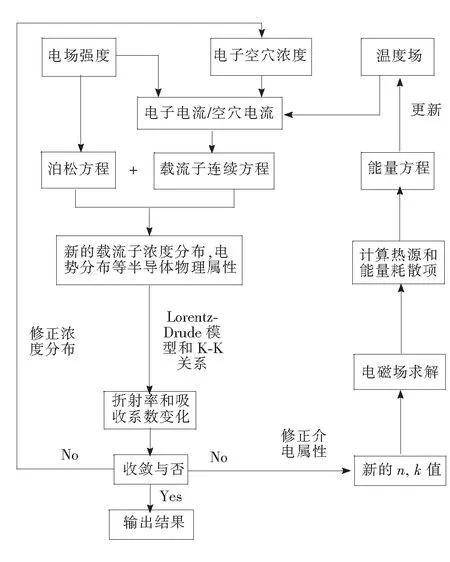
图2 计算流程图

图3 硅基半导体的电磁场、温度场和载流子浓度分布。(a) 入射光电场模分布;(b) 温度场分布;(c) 温度梯度分布;(d) 半导体内电场模分布;(e) 半导体内电位移矢量分布;(f) 电势分布;(g) 电子浓度分布;(h) 空穴浓度分布;(i) 德拜长度分布。
Fig.3 Electromagnetic field, temperature field, and carriers concentration distribution in the silicon based semiconductor. (a) Electric field norm of incident light. (b) Temperature field distribution. (c) Temperature gradient. (d) Electric field norm in semiconductor. (e) Potential shift vector in semiconductor. (f) Electric potential distribution. (g) Electron concentration. (h) Hole concentration. (i) Debye length.
求解时,首先对半导体进行电域分析,获得在外加电场作用下的均一温度场下的载流子分布,并根据上述载流子分布计算获得半导体内的折射率和吸收系数分布;然后再对该计算域进行光域分析,讨论外界激光照射下半导体对光的吸收以及透反射特性;最后对其传热属性进行分析,根据光吸收计算获得热沉积项并作为热源生成项代入到能量方程中,在给定热边界条件下计算获得半导体介质内的热流密度和温度分布,将该温度分布代入到漂移扩散方程中,重新计算载流子浓度分布。依照上述过程进行反复迭代,最终当接收屏⑦上的波形达到稳定不变时,认为计算已经达到收敛。具体计算流程如图2所示。
图3分别显示了电压反接、电压为5 V时整个系统的电场模值分布,以及半导体内部的电子浓度、空穴浓度、电场模、电势、温度和温度梯度分布。从图中可以看出,半导体对光的吸收集中在表面非常薄的一层区域内。光不能完全穿透硅基半导体,这主要是因为硅基半导体具有很大的吸收系数。而根据计算得到的电子浓度和空穴浓度相对于初始情况下的变化以及初始情况下的折射率和吸收系数分布,可以计算获得不同工况下半导体折射率和吸收系数。
4 结果与讨论
针对入射光波长为0.38 μm、入射光强为4 000 V/m的高斯激光作用下的半导体中的光传输特性及介电物性的变化,本文分别研究了不同接线方式、不同外加电压大小、不同换热系数、不同环境温度和不同初始掺杂浓度情况下的光传输特性,重点分析了半导体中温度、电磁损耗密度、内热源生成量、半导体内部电场模和外部高斯激光电场模的变化,总结出以上变化与影响因素之间的关系。
4.1 外加电压的影响
图4显示了在半导体正接时,半导体内部的最高电子浓度、最低电子浓度、最高空穴浓度、最低空穴浓度与外加电压的变化关系。从图中可以看出,最高电子浓度和最高空穴浓度几乎不随外加电场发生变化。而最低电子浓度和最低空穴浓度则会随着电压的升高而略有增大。这主要是因为在初始情况下,正负载流子分别集中在P区和N区,随着两极间电压的增大,载流子迁移率增大,其向另一端迁移变得更加容易,使得载流子浓度向着分布更加均匀的趋势变化。

图4 半导体载流子浓度随电压的变化关系(正接)
Fig.4 Relationship between carriers concentration of semiconductor and voltage variation (positive bias voltage)
表1显示了电压正接时,半导体内部和外部各项参数随着外加电压的变化关系。可以看出半导体温度、电磁能损耗、内热源生成均随着电压的增大而逐渐增大,而半导体外部电场模和半导体内部的电场模值的最大值均随着电压的增大而减小。这主要是因为随着电压的增大,光吸收薄层区域内的空穴数目减小而电子数目增多,由于相同数目的电子变化对吸收系数的影响要大于空穴的影响,故该薄层区域内的吸收系数增大。这导致电磁耗散密度增加,生成内热源也逐渐增加,入射光能量被吸收的份额增多,被反射的份额减小,因此外部高斯光的电场模略有降低。
图5显示了在半导体反接时,半导体内部的最高电子浓度、最低电子浓度、最高空穴浓度、最低空穴浓度随外加电压的变化关系。从图中可以看出,最高电子浓度和最高空穴浓度几乎不随外加电场发生变化,而最低电子浓度和最低空穴浓度则会随着电压的升高而略有减小,其中空穴浓度的减小大于电子浓度。这主要是由于初始状态下在半导体中空穴占据的体积较少,在电场作用下其需要迁移的距离要大于电子,因此在整个区域内空穴浓度变化较大。此外,与图4不同的是,由于半导体PN结的单向导通性,此时电子和空穴的最小值发生急剧下降而不是上升,导致在电子和空穴的交界区域产生一个载流子稀薄区,从而使最低电子浓度和空穴浓度均减小。
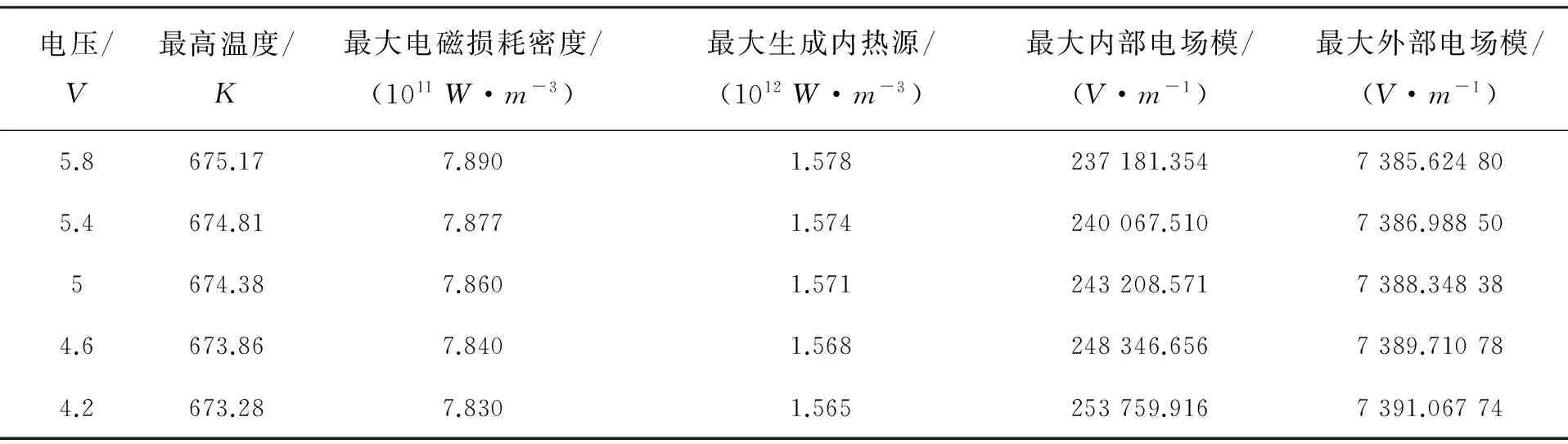
表1 半导体各项参数随外加电压大小的变化(正接)

图5 半导体载流子浓度随电压的变化关系(反接)
Fig.5 Relationship between carriers concentration of semiconductor and voltage variation (reverse bias voltage)
表2显示了电极反接时,半导体内部和外部各项参数随电压的变化关系。从表中可以看出,半导体温度随着电压的增大而逐渐降低,另外此时的电磁能损耗密度、内热源生成量、半导体外部电场模值都变化不大,而半导体内的电场模随着电压的减小而减小。这主要是因为电压反接时PN结处于非导通状态,在光吸收的薄层区域内载流子浓度变化不大,导致吸收系数也基本没发生变化。而由于此时在载流子复合的交界区附近的电子和空穴浓度随电压增大都是减小的,该处的吸收系数变小,故对应的内部电场模反而增大。

表2 半导体各项参数随外加电压大小的变化(反接)
4.2 换热系数的影响
图6显示了电压正接且大小为5 V时,半导体内部的最高电子浓度、最低电子浓度、最高空穴浓度、最低空穴浓度随换热系数的变化关系。从图中可以看出,最高电子浓度和最高空穴浓度随着换热系数几乎不发生改变,而最低电子浓度和最低空穴浓度则会随着换热系数的增大而逐渐减小,且当换热系数越高时减小的幅度越小。这主要是因为换热系数增大时温度会降低,导致热激发效应减弱,因此电子浓度和空穴浓度都相应减小,而温度降低的幅度随着换热系数的增大逐渐减小。
表3显示了正接情况下,半导体内部和外部的各个参数随换热系数的变化关系。从图中可以看出,温度随换热系数的增大而逐渐降低,但降低幅度减慢;而电磁能损耗密度和内热源生成量随换热系数的增大均呈现出先减小后增大的趋势,其中换热系数为10 W/(m2·K)时的电磁能损耗密度和内热源生成最小。半导体内电场模的最大值随着换热系数的增大而减小,而外部高斯光电场模的最大值随着换热系数的增大先逐渐增大,最终几乎趋于定值。
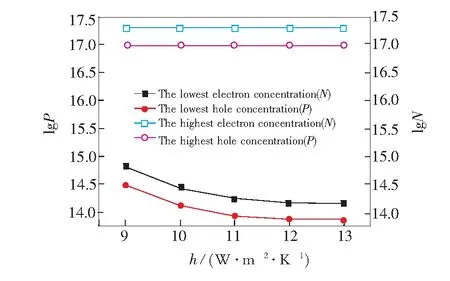
图6 半导体载流子浓度随对流换热系数的关系(正接)
Fig.6 Relationship between carriers concentration of semiconductor and heat transfer coefficient(positive bias voltage)
造成以上现象的主要原因,在于此时的电子浓度下部高上部低,而空穴浓度上部高下部低。激光照射到晶体上主要是被晶体上表面很薄的一层介质吸收,该区域的吸收系数是影响整个电磁能量损耗密度和内热源大小的关键。此时的吸收系数主要受到电子浓度的低值和空穴浓度的高值共同作用的影响。根据方程(15),吸收系数与当地的电子和空穴浓度都有关系,决定能量损耗和热源生成的主要是吸收系数大小,而界面反射率(可以根据折射率计算获得)则会影响外部高斯光电场模的数值。在薄层内的光吸收和介质表面的光反射变化决定了电磁能损耗、内热源生成和半导体外部电场模呈上述规律分布。而随着换热系数逐渐减小,半导体内部温度升高,导致载流子扩散能力增强,增大了电子电流和空穴电流,从而使得内部电场模增加。
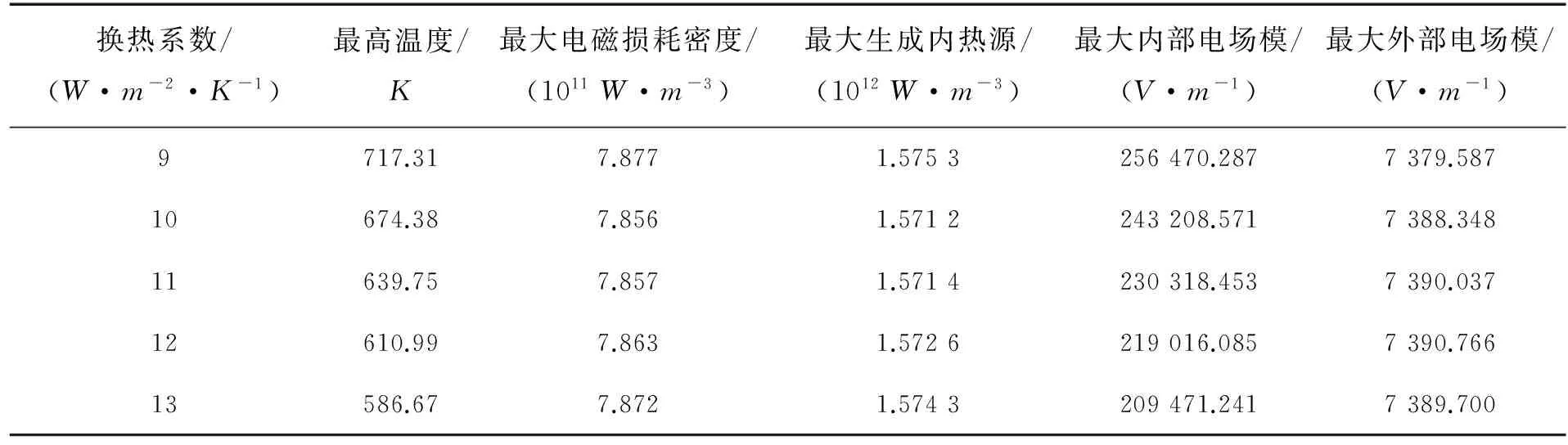
表3 半导体各项参数随换热系数的变化(正接)
4.3 环境温度的影响
图7显示了电压正偏且大小为5 V时,半导体内部的最高电子浓度、最低电子浓度、最高空穴浓度、最低空穴浓度随环境温度的变化关系。从图中可以看出,最高电子浓度和最高空穴浓度随环境温度几乎不改变,而最低电子浓度和最低空穴浓度则会随着环境温度的升高而逐渐升高,且随环境温度升高变化的幅度略有增大。这主要是因为晶体温度随着环境温度的升高而升高,导致热激发效应增强,因此电子浓度和空穴浓度都相应增大,而温度升高的幅度值随着环境温度的升高也逐渐增大。

图7 半导体载流子浓度随环境温度的关系(正接)
Fig.7 Relationship between carriers concentration of semiconductor and environment temperature (positive bias voltage)
表4显示了电压正偏情况下,半导体内部和外部的各个参数随环境温度的变化关系。从表中可以看出,电磁能损耗密度、内热源生成量和最大内部电场模均随环境温度的升高而增大,而外部电场模随着环境温度的升高而略有减小。
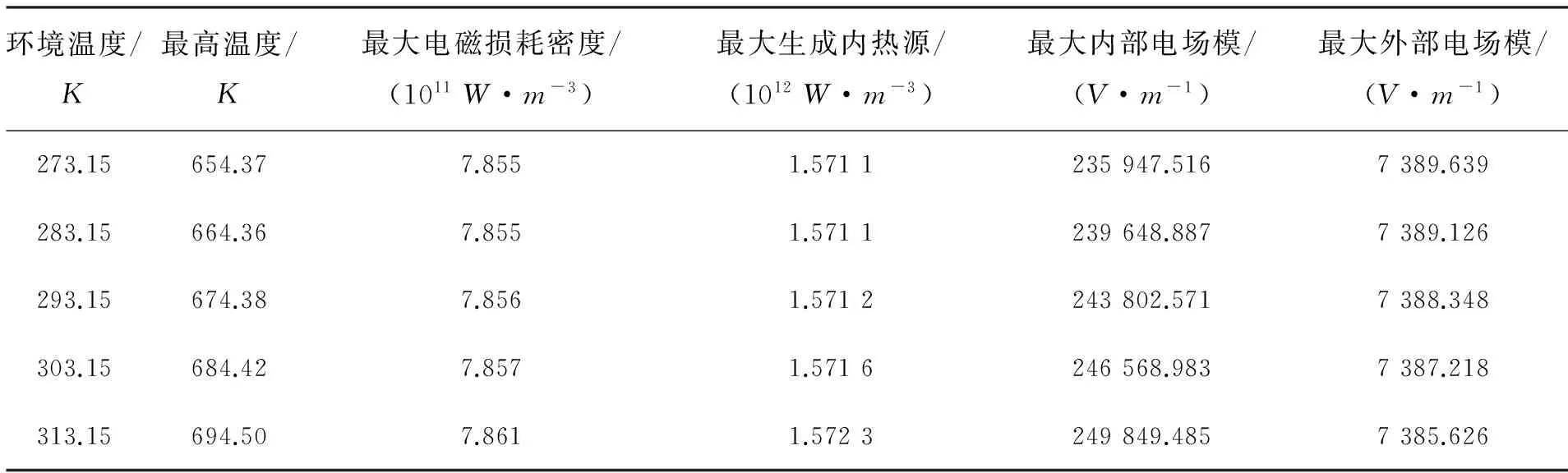
表4 半导体各项参数随环境温度的变化(正接)
4.4 初始注入浓度的影响
图8显示了电压正接且大小为5 V时,半导体内部的最高电子浓度、最低电子浓度、最高空穴浓度、最低空穴浓度(均用C表示)随对应初始注入浓度C0的变化关系,从图中可以看出,最高电子浓度和最高空穴浓度均随着初始掺杂浓度的增加而增大,而最低电子浓度和最低空穴浓度随着初始掺杂浓度的增大而减小。这主要是因为初始掺杂浓度的提高增大了电子电流和空穴电流中的浓度扩散项,因此造成了半导体内部载流子浓度差的扩大。

图8 半导体载流子浓度随初始注入浓度的关系(正接)
Fig.8 Relationship between carriers concentration of semiconductor and initial injection concentration (positive bias voltage)
表5显示了电压正接且大小为5 V时,半导体内部和外部的各个参数随初始注入浓度的变化关系。可以看出,半导体温度随着浓度的增大而逐渐增大,但变化幅度逐渐变得平缓,此外晶体内的最高和最低温度基本相差不大。这主要是因为样品的尺度很小。从表中还可以发现,电磁能损耗密度和内热源生成量都随着初始浓度的升高而增大。这主要是因为此时的吸收系数主要由上部的电子浓度和空穴浓度决定,电子浓度分布是上边低下边高,而空穴浓度是上高下低。从图8可以看出,在半导体顶部电子浓度的最低值基本保持不变,而空穴浓度的最高值随着初始浓度的增大而增大,因此半导体上表面附近的吸收系数随初始掺杂浓度的增大而增大,造成温度、电磁损耗密度和内热源呈上述规律变化。另外,由于增大浓度后加强了浓差扩散,半导体中电场模的最大值随着初始浓度值的增大而增大;而由于增大浓度后光吸收增加,导致反射光的能量被削弱,造成外部高斯光电场模的最大值随着浓度的增大而减小。

表5 半导体各项参数随初始注入浓度的变化(正接)
4.5 硅基电热调控原理
从上述模拟结果可以看出,当电压正偏时,随着电压的升高,电子浓度和空穴浓度的最低值均会增大;而随着换热系数的增大或环境温度的降低,电子浓度和空穴浓度的最低值均相应减小。由此可以看出,在一定范围内,电压的升高与晶体温度的降低对载流子浓度扩散的影响是截然相反的。由于电子浓度和空穴浓度的分布又决定了介质折射率和吸收系数的大小,而上文中的分析已经说明反射光强度主要由P区上部薄层内的复折射率决定,因此,通过调节P区上部薄层内的电子浓度和空穴浓度,应该可以改变折射率和吸收系数,从而影响高斯光被吸收/被反射的份额,维持接收屏上的信号在一个稳定的范围内。即如同文献[15]针对铌酸锂晶体电热调控提到的那样:通过改变外加电压的大小来调控热边界条件的影响,从而使接收屏上的信号维持恒定不变。为了研究在硅基半导体中是否也存在类似性质,我们通过载流子浓度对⑨这一点的折射率和吸收系数进行了计算。表6所示为电压正接且大小为5 V、环境温度恒为293.15 K时,位置⑨处的复折射率的实部和虚部随换热系数的变化关系。表7所示为环境温度恒为293.15 K、换热系数恒为10 W/(m2·K)时,位置⑨处的复折射率的实部和虚部随正接外加电压的变化关系。
从表6和表7可以看出在上述工况内,复折射率实部随着换热系数的增大和电压的升高而减小,而复折射率虚部随着换热系数的增大和电压的升高而增大,且复折射率实部随电压或换热系数的变化量要远大于虚部的变化量。这表明在一定工况范围内,升高电压与增大换热系数造成复折射率的变化规律是相同的。
半导体P区表面的折射率和吸收系数的变化使得接收屏上的信号也相应发生改变。图9显示了不同工况下接收屏上电场模随位置的变化。
表6 半导体复折射率随换热系数的变化关系 (电压正偏)
Tab.6 Influence of heat transfer coefficient on complex refractive index (positive bias voltage)

换热系数/(W·m-2·K-1)n/ωk/ω101.90490.93389111.89980.93397121.89540.93407131.88790.93418
表7 半导体复折射率随外加电压的变化关系(电压正偏)
Tab.7 Influence of bias voltage on the parameters of complex refractive index (positive bias voltage)
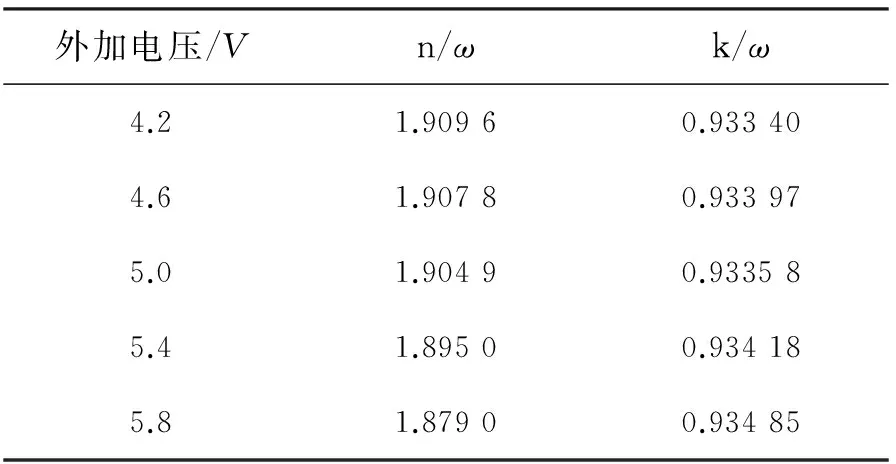
外加电压/Vn/ωk/ω4.21.90960.933404.61.90780.933975.01.90490.933585.41.89500.934185.81.87900.93485

图9 不同情况下,接收屏上的电场强度分布。
可以看出,接收屏上的电场模随着电压的降低而增大,随着换热系数的增大而减小,但整个波形并未发生变化。造成上述现象的原因在于反射率与折射率之间存在以下关系:
(16)
式中,n1为P结表面的折射率,n2为空气的折射率,此处n2设为1。容易证明,当n1大于1时,反射率随着表面折射率的增大而逐渐增大。结合表6、表7可知,减小换热系数和降低电压均会增大P结表面的折射率,从而增大反射率,导致接收屏上的电场模值增大。因此,可以通过调整外加电压来增强或减弱温度效应对介质折射率和吸收系数的影响,从而控制光的反射方向和振幅,使得接收屏的光信号保持不变。从模拟计算的结果得知,在电压为5 V、换热系数为10 W/(m2·K)的晶体上将施加的电压增加到5.246 5 V,或在电压为5 V、换热系数为13 W/(m2·K)的晶体上将施加的电压降低到4.858 8 V,均可以使得接收屏上的光波形变得跟电压为5 V、换热系数为12 W/(m2·K)的工况时一致,如图10所示,从而验证了硅基半导体中电热调控方案的可行性,即在硅基材料中也可以通过调节外加电压抵消温度升高对接收屏上反射光模值的改变。此外,由于增大换热系数和降低环境温度对半导体本身温度的影响一致,所以改变外加电压不仅可以抵消换热系数变化带来的影响,也可抵消环境温度变化带来的影响。

图10 3种不同情形下,接收屏上的电场强度信号。
Fig.10 Electric field intensity signal on the screen in three different cases
5 结 论
通过有限元法求解电磁场波动方程、能量方程和半导体基本方程的耦合方程组,在同时考虑电场、温度场和载流子浓度场共同作用的情况下,对高斯激光作用下的半导体内的载流子输运、电磁场和温度场特性以及能量损耗进行了讨论,研究了不同外加电压、不同换热系数和不同初始载流子的影响,得出结论如下:(1)正接时,最低电子浓度和最低空穴浓度会随着电压的升高而略有增大,温度和半导体内的能量损耗随电压升高而增大。(2)反接时,最低电子浓度和最低空穴浓度会随着电压的升高而减小,温度随着电压的增大而逐渐降低,半导体内的电场模随着电压的减小而减小。(3)正接时,最低电子浓度和最低空穴浓度会随着换热系数的增大和环境温度的降低而逐渐减小,且当换热系数越高时减小的幅度越慢。(4)正接时,半导体温度随着初始浓度的增大而逐渐增大,而电磁能损耗密度和内热源生成量都均随着初始浓度的升高而增大。
研究还证明了在一定范围内升高电压和增大换热系数对接收屏上的电场模分布的影响是相同的,由此证实了硅基半导体中通过电光效应调制热光效应的可行性。本研究对于拓展硅基半导体在电调控领域的应用,尤其是对将来涉及到各种热效应情况下的半导体折射率或吸收系数调控问题起到积极的推进作用。
[1] 周治平. 硅基光电子学 [M]. 北京: 北京大学出版社, 2012. ZHOU Z P.SiliconBasedOptoelectronics[M]. Bejing: Peking University Press, 2012. (in Chinese)
[2] WANG X L. SOI thermo-optic modulation with fast response [J].Chin.Opt.Lett., 2003, 1(9):527-528.
[3] OHEDA H. Change in the optical-absorption coefficient induced by optical modulation of the internal electric field in doping-modulated amorphous silicon multilayers [J].J.Appl.Phys., 1990, 67(10):6476-6480.
[4] LIU A, LIAO L, RUBIN D,etal.. High-speed optical modulation based on carrier depletion in a silicon waveguide [J].Opt.Express, 2007, 15(2):660-668.
[5] RAO S, D’ADDIO C, DELLA CORTE F G. All-optical modulation in a CMOS-compatible amorphous silicon-based device [J].J.Eur.Opt.Soc., 2012, 7:12023-12025.
[6] 王兴军,周治平. 硅基光电集成用铒硅酸盐化合物光源材料和器件的研究进展 [J]. 中国光学, 2014, 7(2):274-280. WANG X J, ZHOU Z P. Research progress of Er silicate compound light source materials and devices for silicon photonics application [J].Chin.Opt., 2014, 7(2):274-280. (in Chinese)
[7] 朱景程. 场致线性电光效应及其在硅基光电子学中的应用研究 [D]. 长春: 吉林大学, 2012. ZHU J C.StudiesofTheElectric-field-inducedLinearElectro-opticEffectandItsApplicationsinSiliconOptoelectronics[D]. Changchun: Jilin University, 2012. (in Chinese)
[8] CAO L, ABOKETAF A, WANG Z H,etal.. Hybrid amorphous silicon (a-Si∶H)-LiNbO3electro-optic modulator [J].Opt.Commun., 2013, 139(1):233-240.
[9] CHMIELAK B, MATHEISEN C, RIPPERDA C. Investigation of local strain distribution and linear electro-optic effect in strained silicon waveguides [J].Opt.Express, 2013, 21(21):25324-25332.
[10] NOBORISAKA J, NISHIGUCHI K, FUJWARA A. Electric tuning of direct-indirect optical transitions in silicon [J].Sci.Rep., 2014, 4:6950-6955.
[11] SELBERHERR S.AnalysisandSimulationofSemiconductorDevices[M]. Vienna: Springer, 1984.
[12] LINDEFELT U. Current-density relations for non-isothermal modeling of degenerate hetero-structure device [J].J.Appl.Phys., 1994, 75(2):958-966.
[13] MARSHAK A H, VLIET C M. Electrical current and carrier density in degenerate material with nonuniform band structure [J].Proc.IEEE, 1964, 72(2):148-164
[14] VIVIEN L, PAVESI L.HandbookofSiliconPhotonics[M]. Boca Raton: CRC Press, 2013.
[15] ZHOU J, HE Z H, MA Y,etal.. Study of light-absorbing crystal birefringence and electrical modulation mechanisms for coupled thermal-optical effects [J].Appl.Opt., 2014, 53(27):6243-6255.

周吉(1986-),男,湖南湘潭人,博士研究生,2011年于重庆大学获得硕士学位,主要从事电光热多场耦合下的光传输效应的研究。
E-mail: zhouji174@163.com

贺志宏(1973-),女,黑龙江海宁人,副教授,硕士生导师,2001年于哈尔滨工业大学获得博士学位,主要从事电光热多物理场耦合辐射特性的研究。
E-mail: zhihong_he@hit.edu.cn
Optical Transmission and Electrical Modulation for Silicone Semiconductor with Multi-field Effect
ZHOU Ji1,2, HE Zhi-hong1*, YU Xiao-jun3, YANG Dong-lai3, DONG Shi-kui1
(1.SchoolofEnergyScienceandEngineering,HarbinInstituteofTechnology,Harbin150001,China;2.ChinaAcademyofSpaceTechnology, 508Institute,Beijing100094,China; 3.ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China)*CorrespondingAuthor,E-mail:zhihong_he@hit.edu.cn
In order to study the silicon based semiconductor’s electro-optic-thermal muti-field coupling characteristics and electric modulation problems, both the Poisson equation and the carrier continuity equation were introduced to calculate the carrier concentration distribution in the carrier transport procession. Drude Lorentz relation and K-K relation were also employed to discuss the effect of the carrier concentration on the refractive index and absorption coefficient. The heat deposited items were obtained by calculating electromagnetic dissipation. The coupled semiconductor basic equation, electromagnetic wave equation and energy equation were solved by using finite element method. With the effect of external voltage, initial concentration of carrier and heat transfer coefficient, the change of dielectric properties, optical transmission behavior of silicon based semiconductor were also analyzed by coupling solution and analysis. The results show that the reflective optical field mode of the semiconductor P area increases with the increasing of the applied voltage, and decreases with the increasing of the heat transfer coefficient. Using this mechanism, a scheme of electric thermal modulation for the space distribution of the reflection intensity was presented.
silicone semiconductor; carrier concentration; thermo-optic effect; electro-optic effect; electro-thermal modulator
1000-7032(2016)01-0063-11
2015-10-08;
2015-11-12
国家自然科学基金(51176039,51576054)资助项目
TK124
A
10.3788/fgxb20163701.0063

