高校分布式信息管理系统加密优化探析

刘闫锋

高校分布式信息管理系统加密优化探析

刘闫锋

分布式信息管理系统在高校管理中被广泛应用，该系统对传输数据的高效安全有很高要求。本文通过对原有的加密算法进行优化，构造出较高运算效率的混合加密体系，满足消息认证与密钥管理。实验表明，混合加密体系具有可靠的可行性与安全性，效率也明显有所提升。

分布式 信息管理 混合加密

科研项目：2015年陕西省教育厅专项科研计划项目（2015KJ1178）。

信息技术的快速发展，分布式信息管理系统因其投入小的优点被人们大量应用。分布式信息管理系统需要面临大量的数据交互。对数据进行加密是保障信息安全的主要手段，加密的两个种类为对称加密和非对称加密，对称加密算法具有效率高、算法简单、系统开销小、适合大量数据加密的特点，代表算法有3DES算法、IDEA算法、RC5算法等。非对称加密算法具有分解安全性高、易于实现、能够进行身份认证等特点，代表算法有RSA算法、Elgamal算法等。

目前多校区高校财务管理信息系统基本采用对称加密算法进行数据加密，其适合大数据量的数据加密与传输、具有速度快、安全性能高的特点。3DES算法已发展成熟，具有易实现的优点，然而在多消息传输中安全性不能保证，造成大数据传输效率低下的一个主要原因是签名认证消耗时间太多。解决系统数据加密面临的问题，一般采用3DES算法与RSA算法结合的混合加密算法方式。

混合加密算法

1.两种算法的优缺点

（1）密钥管理方面，3DEES算法只有不断更新密钥才能保证数据的安全，密钥生命周期有限，RSA算法在密钥管理方面明显优于3DES算法。3DES算法是对称加密算法，鉴于对称加密算法的特点，容易在密钥分配传递中泄露密钥，具有密钥管理难度高、更换困难、风险大的缺点。RSA算法只需要保证私钥的安全，对加密密钥更新容易。

（2）加解密效率方面，3DES算法适用于大量快速的加解密运算，可以通过计算机编程快速实现替换和位移。RSA算法使用高阶模幂运算进行加解密过程，比较耗时，不适合大量多次数据加密。

（3）身份认证和消息验证方面，RSA算法可以非常容易地实现身份验证和数字签名。3DES算法无法使用一个密钥进行数字签名。

2.混合加密算法

本文在分析3DES和RSA两种算法优缺点的基础上，对RSA算法的加解密运算进行优化，提出了一种既能够快速加解密也能进行身份验证和数字签名的混合加密体制。其实现过程如下：

(1）信息(明文)采用DES密钥加密；

(2）使用RSA加密前面的DES密钥信息；

(3）最终将混合信息进行传递；

(4）而接收方接收到信息后；

(5）用RSA解密DES密钥信息；

(6）再用RSA解密获取到的密钥信息解密密文信息；

(7）最终就可以得到我们要的信息(明文)。

算法优化与数字签名

1.RSA算法优化

本文从快速指数法和孙子定理两方面对RSA算法进行优化：

（1）用快速指数法优化RSA算法:幂计算在RSA系统中的利用率极高，分别涉及索性检测、加密、解密和乘法逆元。作为RSA算法的关键部分，耗时问题一直制约着它的广泛应用。我们使用快速指数算法解决优化幂计算问题。下面给出一个计算Xrmodn的快速算法：

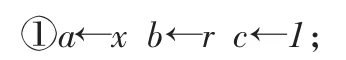
②如果b=0，则输出结果c，结束；

③如果bmod2≠0，则转到第5）步；

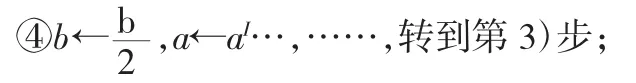
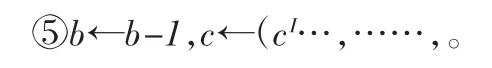
（2）孙子定理优化算法：为了追求效率我们不能只选择小数值，运用孙子定理（中国剩余定理）加快运算速度。中国剩余定理（是数论中最有用的定理之一）可以对两两互素的整数取模得到一组剩余类数，通过这组剩余类数来重构某一范围内的整数。

在数据加密系统中，如何提高求模的计算速度，当私钥d与n同量级时，解密的速度比较慢。可以利用中国剩余定理降低其数量级，予以简化计算过程。

剩余定理：设m1，m2，mk…是两两互素的正整数，则X= aimodmi，i=1,2…k的唯一正整数解为 x=a1M1y1+a2M2y2+akMkyk（modM）

孙子定理广泛应用在RSA算法加解密过程中，此方法同样需要素数p和q，用（d，p，q）代替密钥生成算法要输出的私有密钥（d，n）。利用孙子定理计算，解密模数（密文、密钥和明文数据）比原来的要小。

（3）大素数生成与检测：大素数的产生使用随机递增搜索法，现有的文献已经证明随机递增搜索次数要小于随机搜索法。我们在找到一个素数之前，要测试大约lnN个整数，由素数定理可知，在N附近的一个素数平均隔lnN个整数。实际上只要测试大约（lnN）/2个整数，这里采取了直接拒绝偶数做法。我们可以在进行索性检测前进行排除偶数预处理，这样可以提升检测效率，使用小素数整除法进一步筛选，然后检测伪素数的索性。通过多次测试可以使得一个整数接近素数的概率达到1.0。看起来繁琐的过程，其实也不会繁琐，执行这个过程是为了得到一对新的密钥。

2.数字签名过程

RSA算法也用于身份认证与数字签名方面，它的功能不再仅仅是加解密。使用散列函数作为验证码可以增加效率、减少签名时间、提高保密度，通过散列函数可以生成一个散列值作为消息验证码。签名过程如下：

（1）发送方将M通过散列函数进行计算，产生一个散列值h，h=H（M），H（M）是定长的散列值，M是需要传输的消息；

（2）发送方用私钥加密h，产生数字签名S=hdmodn；

（3）接收方将发送方消息M和签名S一同接收；

（4）接收方用公钥解密签名S得到h，用H计算得到h′，假如h′=h，则说明消息没有被篡改，消息正确；如果h′≠h，说明消息来源出现问题。这样避免了在消息传输过程中消息来源问题和中间人篡改消息的情况发生。

实验结果

实验测试环境：i7-6700CP U、8G内存，，VisualStudio2010开发工具，Windows7操作系统。

1.RSA签名效率与加密速率测试

我们以512位素数为例，测试大量素数生成效率，如表1所示经典算法与改进算法的执行效率。实验表明，随着素数位数的增加，实验消耗时间的增加量明显有所改善，足以说明通过缩短素数时间提高RSA签名效率是可行的。

表1 经典算法与改进算法生成大素数时间对比表

我们使用生成1024位素数测试RSA签名速率，并和传统RSA签名进行对比。如表2所示，改进的签名计算过程效率提升非常明显，可以大幅度提高RSA加解密速度，可以有效地应用在大数据传输的消息认证中。

我们使用生成素数对RSA签名速率进行测试，使用传统RSA与改进RSA签名进行对比。如表2所示，改进的签名计算可以提高加解密速度，签名效率提升非常明显，在大数据传输的消息认证中可以有效地应用RSA签名。

2.安全性分析

密钥管理与消息认证是混合加密体系主要的安全风险所在。基于算法的安全性是密钥管理的主要风险，RSA算法在模数够大时安全性才有保证。进行密钥更换和分配必须在密钥管理方法体系下严格执行。消息认证方面，直接使用散列函数计算散列值，避免了人为篡改、中间人攻击和伪造签名的风险。

表2 改进签名与传统RSA签名时间对比表

结语

本文以多校区财务管理信息系统为例，面对密钥管理安全和系统传输信息的需要，综合分析了非对称加密算法（RSA）和对称加密算法（3D ES）的不同。结合RSA和3D ES两个算法的优缺点，对其功能进行了研究分析，优化部分计算过程，研究混合加密体系，提高了系统运行安全性，解决系统消息认证与密钥管理问题，同时提出一种解决分布式管理系统数据安全问题的思路。

在后续的研究中，将会继续优化加密过程以提高运算速度，并将混合加密体系推广到其他分布式信息管理系统中，在消息认证与身份认证方面作深入研究。

[1]张宝华：《RSA算法的安全及有效实现》，《中山大学学报》（自然科学版）2014年第30卷第8期，第27-31页。

[2]石井：《RSA数据加密算法的分析与改进》，《济南大学学报》（自然科学版）2013年第27卷第3期：第283-286页。

[3]贺克英：《改进的RSA算法实现研究》，成都电子科技大学，2014。

[4]费晓飞：《CRT-RSA算法安全性分析》，《微计算机信息》2013年第25卷第3期，第54-55页。

[5]雷文：《一种大素数快速生成算法设计与改进》，《四川理工学院学报》（自然科学版）2014年第24卷第3期，第313-316页。

[6]胡驰：《AES与RSA算法优化及其混合加密体制》，《计算机应用研究》2014年第31卷第4期，第1189-1194页。

作者单位：陕西学前师范学院 陕西西安