基于变分模态分解改进方法的滚动轴承故障特征提取

高红玮， 张丽荣， 侯少杰

(1. 河北经贸大学计算机中心，河北 石家庄 050061；2. 河北经贸大学旅游学院，河北 石家庄 050061)

基于变分模态分解改进方法的滚动轴承故障特征提取

高红玮1， 张丽荣2， 侯少杰1

(1. 河北经贸大学计算机中心，河北 石家庄 050061；2. 河北经贸大学旅游学院，河北 石家庄 050061)

针对滚动轴承早期故障振动信号信噪比低、故障特征提取困难的问题，提出了基于多相关-变分模态分解(MC-VMD)的滚动轴承故障诊断方法。首先对多加速度传感器采集到的信号进行多相关处理以突出故障信号特征；然后通过VMD自适应地将信号分解成多个本征模态分量(IMFs)，运用谱峭度法和包络解调对相关峭度较大的分量进行分析；最后通过包络谱识别出滚动轴承的工作状态和故障类型。将该方法应用到滚动轴承故障实例数据中，实验结果表明，该方法可有效提取滚动轴承故障特征频率信息。

多相关；变分模态分解；滚动轴承；谱峭度

滚动轴承是各种旋转机械中应用最广泛的零部件之一，同时也极易发生损坏。许多重大故障都是由于滚动轴承损坏而产生的，滚动轴承使用寿命直接影响到机械设备运行稳定性和安全性，因此对滚动轴承早期微弱故障的分析与诊断具有重要的科学意义和应用价值。

在90年代末，Wu和Huang[1]提出了经验模态分解(empirical mode decomposition，EMD)算法，这是目前广泛使用的一种自适应信号处理方法，把非平稳信号分解成不同频段的模态分量进而转化成平稳信号进行分析。近年来，基于经验模态分解的HHT(Hilbert-Huang Transform)时频分析技术在处理非线性、非平稳信号中取得了比较满意的效果，得到了广泛的应用[2-5]，但EMD存在模态混叠导致信号分解时频率不能完全分离。为了抑制EMD的模态混叠，Huang进一步提出了EEMD算法，通过加入随机高斯白噪声以消除原信号的噪声。周智等[6]将EEMD应用到滚动轴承的故障诊断中，成功的提取到了故障频率，但是EEMD只是在一定程度上克服了EMD的模态混叠现象，分析结果仍然存在模态混叠。最近，Dragomiretskiy和 Zosso[7]提出一种自适应信号处理新方法——变分模态分解(variational mode decomposition，VMD)，该方法在获取分解分量的过程中通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽，从而能够自适应地实现信号的频域剖分及各分量的有效分离。相比EMD和EEMD的递归“筛选”模态，VMD将信号分解转化非递归、变分模态分解模态，并具有坚实的理论基础，其实质是多个自适应维纳滤波组，表现出更好的噪声鲁棒性，在模态分离方面，VMD可将频率相近的2个纯谐波信号成功分离。Mohanty等[8]将VMD引入到机械故障诊断领域，用于分析滚动轴承故障信号取得了良好的效果。武英杰等[9]将VMD应用于机组传动系统不平衡故障诊断中。有效地避免了噪声及冲击信号造成的模态混叠现象，取得了良好的诊断效果。Muralidharan等[10]将该方法应用于齿轮磨损故障诊断，实现了齿轮的故障特征提取。

将 VMD方法应用于早期故障非稳态信号处理取得了良好的效果，并得到国内外研究人员的广泛认同。然而在强噪声背景下VMD由于抗噪能力不足往往不能很好地实现信号的分离，成为制约VMD方法发展和应用的主要因素。

本文在 VMD算法的基础上，进一步扩展了MC-VMD方法，将其应用到一般振动信号处理中。通过多加速度传感器联合采集振动信号，首先对采集到的信号进行多相关处理，以克服噪声、凸现特征信号；然后通过VMD自适应地将信号分解成多个IMF分量，使得噪声序列的多相关成分仅体现在分解得到的余项中；最后运用谱峭度法和包络解调对相关峭度较大的分量进行分析，通过包络谱识别出滚动轴承的工作状态和故障类型。

1 MC-VMD方法介绍

1.1 VMD原理介绍

VMD分解是基于经典维纳滤波、希尔伯特变换和混频的变分问题求解过程，通过搜寻约束变分模型最优解来实现信号自适应分解，将输入信号分解成一系列具有稀疏特性的模态分量[11-12]。

假设每个模态是具有中心频率的有限带宽，中心频率和带宽在分解过程中不断更新，VMD分解是寻求K个估计带宽之和最小的模态函数uk(t)，模态之和为输入信号f。通过此方法确定每个模态函数的带宽：

(1) 为了获得模态函数的解析信号，对每个模态函数uk(t)进行希尔伯特变换

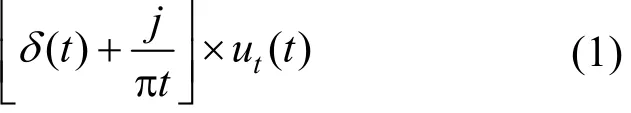
(2) 对各模态解析信号预估中心频率 e-jωkt进行混合，将每个模态的频谱调制到相应的基频带

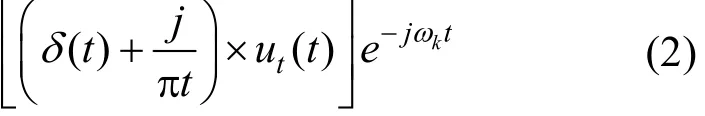
(3) 计算以上解调信号的梯度的平方L2范数，估计出各模态分量的带宽。对应的约束变分模型表达式为

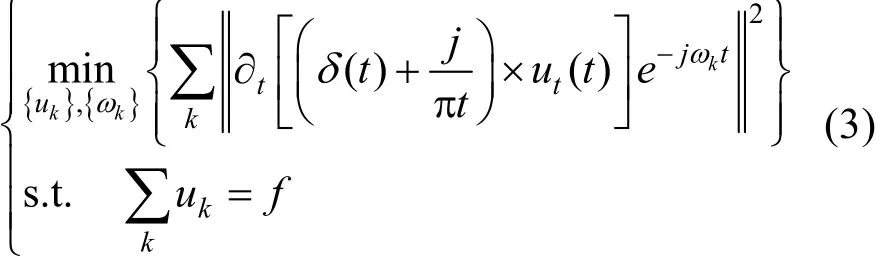
其中，{uk}={u1,…,uk}为分解得到的K个IMF分量；{ωk}={ω1,…,ωk}为各分量的中心频率；为所有模态分量的求和。

为求取上述约束变分问题，引入二次惩罚因子α和Lagrange乘法算子λ(t)，其中二次惩罚因子可在高斯噪声存在的情况下保证信号的重构精度，Lagrange算子使得约束条件保持严格性，扩展的Lagrange表达式为

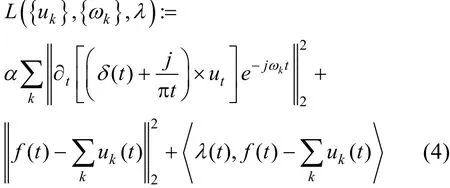
利用交替方向乘子算法(alternate direction method of multipliers，ADMM)求取扩展的Lagrange表达式的“鞍点”。通过执行循环，更新uˆk，ωk，λ进行迭代，得到K个IMF分量。

1.2 MC-VMD原理介绍

振动信号设为x(t)，测量得到的随机噪声n(t)为独立同分布的，且其与x(t)相互独立。此时信号可以表示为

将{x( t), t ∈T }的二次相关函数定义为

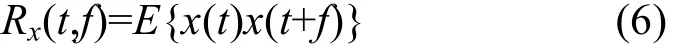
其中，E{.}为统计均值。仿此，定义三次相关函数[12]为

为了简化对三次相关函数的计算，在应用中，取三次相关函数的一个切片f1=f2=f，信号s( t)的三次相关函数表示为

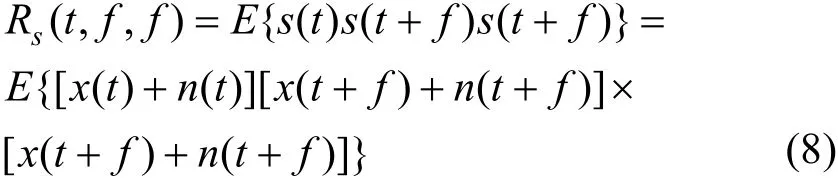
噪声函数的三次相关函数表示为

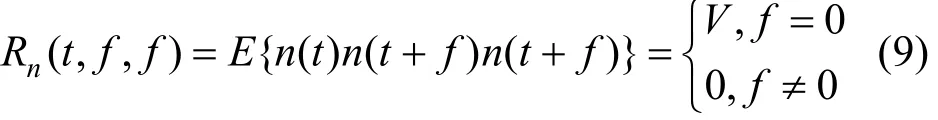
其中，V为常数。式(8)展开为

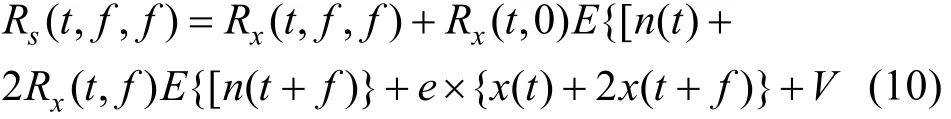
其中， Rx( t, 0) = E{ x( t + f) x( t + f )}。根据实际的应用情况，可以假设系统噪声是零均值的，式(10)可以进一步简化为

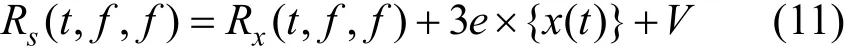
其中，E{x(t)}为采样得到的振动信号的均值；3e × E｛ x( t) ｝+ V为一个常数，即信号s(t)的三次相关函数等于振动信号的三次相关函数与一个常数的和。至此，通过多相关处理，消除了零均值噪声对特征信号的干扰，凸显了特征信号。

在以上基础本文提出了MC-VMD方法，即结合VMD在模态混叠方面的优势和多相关算法的抗噪能力，首先对信号进行多相关处理以突出故障信号特征，之后通过VMD自适应地将信号分解成多个IMF分量，根据EMD的性质，式(7)中分解得到的后两项(即常数项)将会体现在后继分解的余项里面，不影响分解得到的IMF分量。可以看出，通过多相关处理，很好地消除了零均值噪声对特征信号的干扰，使得特征信号凸显，有利于微弱特征信号的特征提取，为后续处理奠定了基础，对提高VMD的效果起到了很好的作用。

2 基于MC-VMD的滚动轴承故障特征提取

如图 1所示，针对滚动轴承早期故障诊断中故障冲击特征微弱等的特点，通过多加速度传感器联合采集振动信号，然后对采集到的信号进行多相关处理以突出故障信号特征，之后通过VMD自适应地将信号分解成多个IMF分量，运用谱峭度法和包络解调对相关系数最大的分量进行分析，最后通过包络谱识别出滚动轴承的工作状态和故障类型。实现的具体步骤如下：

(1) 通过多加速度传感器联合采集振动信号；

(2) 对每个加速度传感器采集的信号进行多相关处理，取三次相关函数的一个切片f1=f2=f，求得相应的多相关函数Rs(t, f, f)；

(3) 对Rs(t, f, f)进行VMD分解，得到各个分量ci(i=1,2,…)；

(4) 分别计算每个IMF分量的互相关系数值、峭度值和峰值因子值，选择三者都较大的分量进行重构，得到多加速度传感器的合成信号；

(5) 对重构后的信号画快速峭度图，获得峭度最大时的中心频率和带宽；根据参数带通滤波后进行包络分析，根据包络谱来判断滚动轴承的工作状态和故障类型。

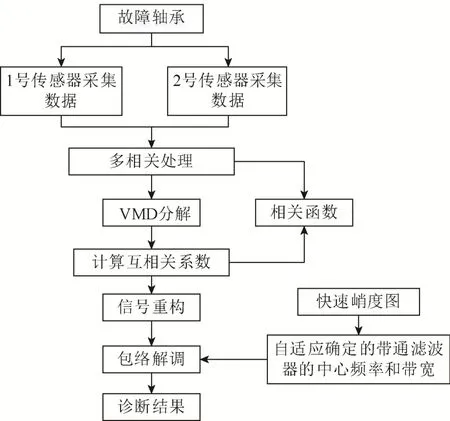
图1 滚动轴承故障诊断流程图

3 基于MC-VMD的滚动轴承故障诊断实例

为了进一步验证本文提出方法在滚动轴承故障特征提取中的有效性，采用实际滚动轴承故障信号进行了验证，实验平台如图2所示的QPZZ-Ⅱ旋转机械故障试验台。信号的采样频率为25 600 Hz，轴承转速为314 r/min。根据滚动轴承的参数(表1)得到理论故障特征频率分别为：内圈故障特征频率37.5 Hz；滚动体故障特征频率26 Hz。

图2 QPZZ-Ⅱ旋转机械故障试验台及故障模型

表1 滚动轴承N205EM参数

3.1 轴承内圈故障诊断

滚动轴承发生内圈故障时，滚动体经过故障位置时会引起冲击振动，内圈转动所引起的冲击振动呈现出周期性的变化，故障表面撞击轴承的其他零部件的表面，产生峰值较高的高频振动序列。采用本文方法对实际采集的振动信号进行处理，内圈故障信号的时域和频域波形如图3所示，对信号进行MC-VMD分析，得到的分解结果如图4所示。由表2可知，IMF1、IMF2与原始信号相关峭度值最大，说明其保留了原信号中最多的冲击特征，故提取这2个IMF进行原信号重构，重构后的故障特征得以增强，接着对消噪后的信号做快速谱峭度图(图5(a))，确定带通滤波器的中心频率为10 400 Hz，带宽为1 600 Hz，对滤波后的信号进行包络分析，得到的包络谱如图5(b)所示。

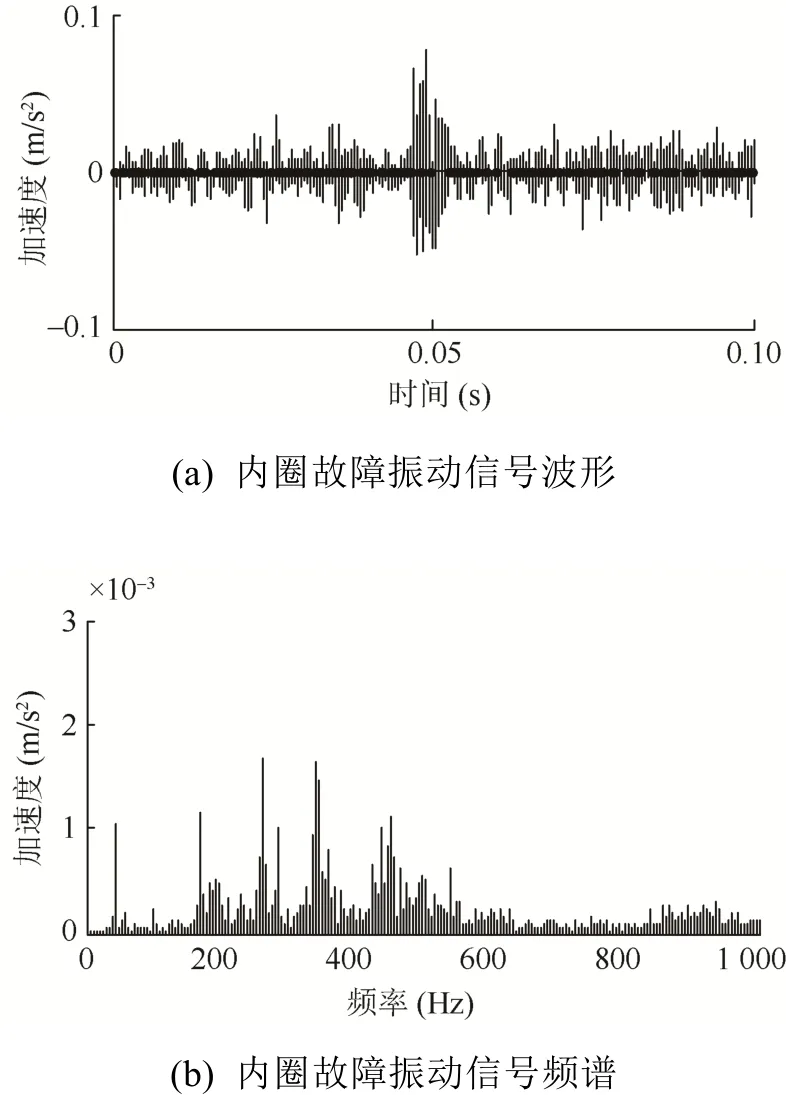
图3 内圈故障信号波形及其频谱

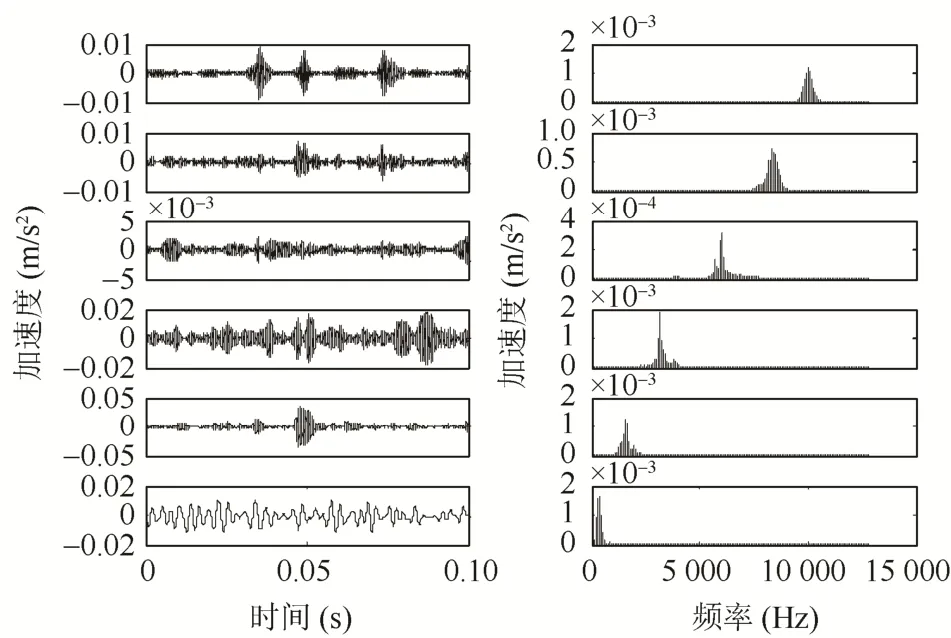
图4 内圈故障信号MC-VMD模态分量波形及频谱

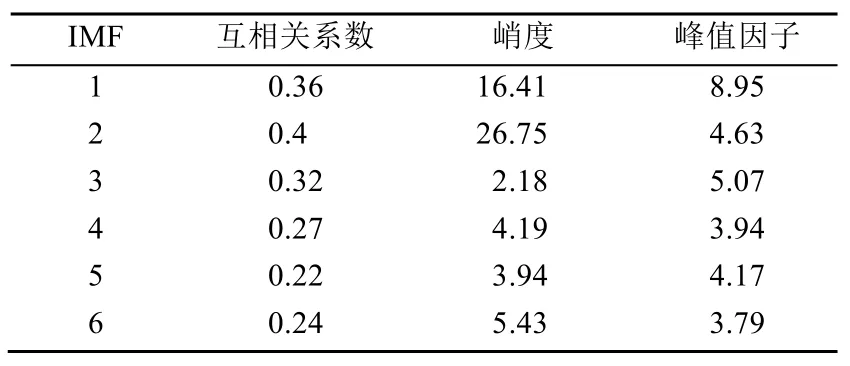
表2 MC-VMD各分量峭度值

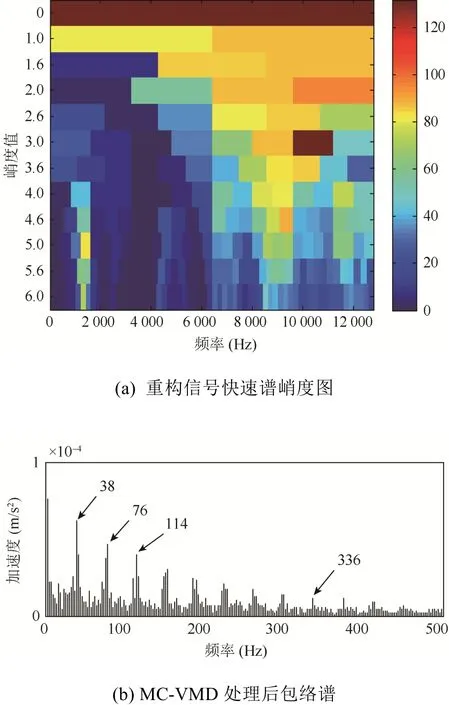
图5 内圈故障信号MC-VMD分析结果

作为对比，采用VMD方法对同一故障信号进行分解，结果如图6(a)所示出现了明显的模态混叠现象。图6(b)为谱峭度方法处理的结果，确定带通滤波器的中心频率为8 800 Hz，带宽为1 600 Hz，通过对比，可以看出原方法中转频及其各阶谐波仍然存在。对其进行包络分析，包络谱如图 6(c)所示。从图5(b)中可以看出，相比于VMD和包络分析的分析结果，本文所用方法受噪声影响较小，抗噪能力明显强于VMD方法，故障特征频率更明显，能够清晰得看到故障特征的1倍频(38 Hz)、2倍频(76 Hz)和3倍频(114 Hz)等各谐波频率，并且噪声成分微弱，凸显了故障特征，能直观有效地分析出故障类型，与理论结果一致。

3.2 滚动轴承滚动体故障分析

当滚动轴承发生滚动体故障时，由于滚动体同时与内外圈接触及受保持架转速的影响，大多数方法通常不能很好地提取出故障特征。滚动体剥落故障信号的时域图和频域图如图 7所示。采用本文方法对实际采集的振动信号进行处理，包络谱如图8(a)所示。作为对比，对信号进行VMD分解和包络分析，得到包络谱如图8(b)所示。对比图8(a)、(b)，VMD分解和包络分析的方法受噪声影响较大，故障特征不明显，本文提出的方法能有效地提取出故障特征 1倍频率(26 Hz)、2倍频(52 Hz)和3倍频(78 Hz)，证明了本文方法在抗噪能力方面的优势。

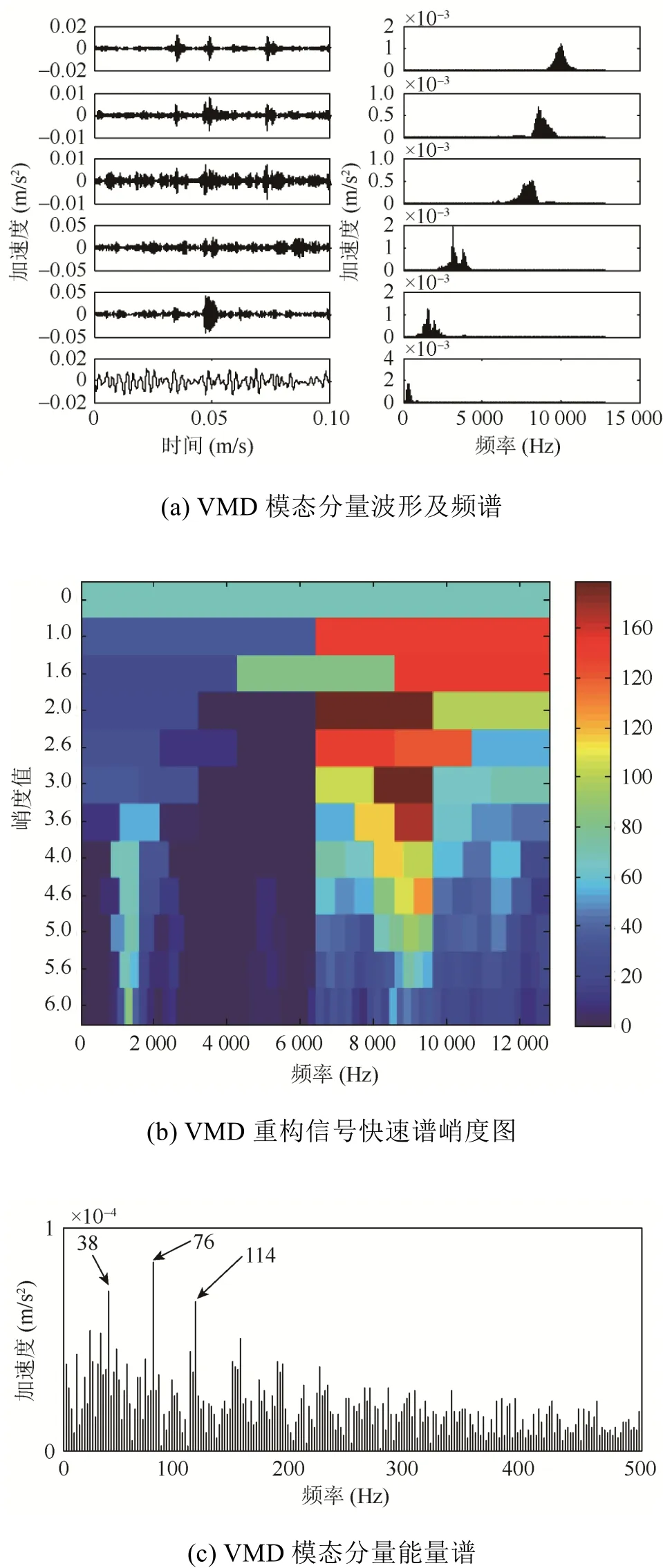
图6 内圈故障信号VMD分析结果

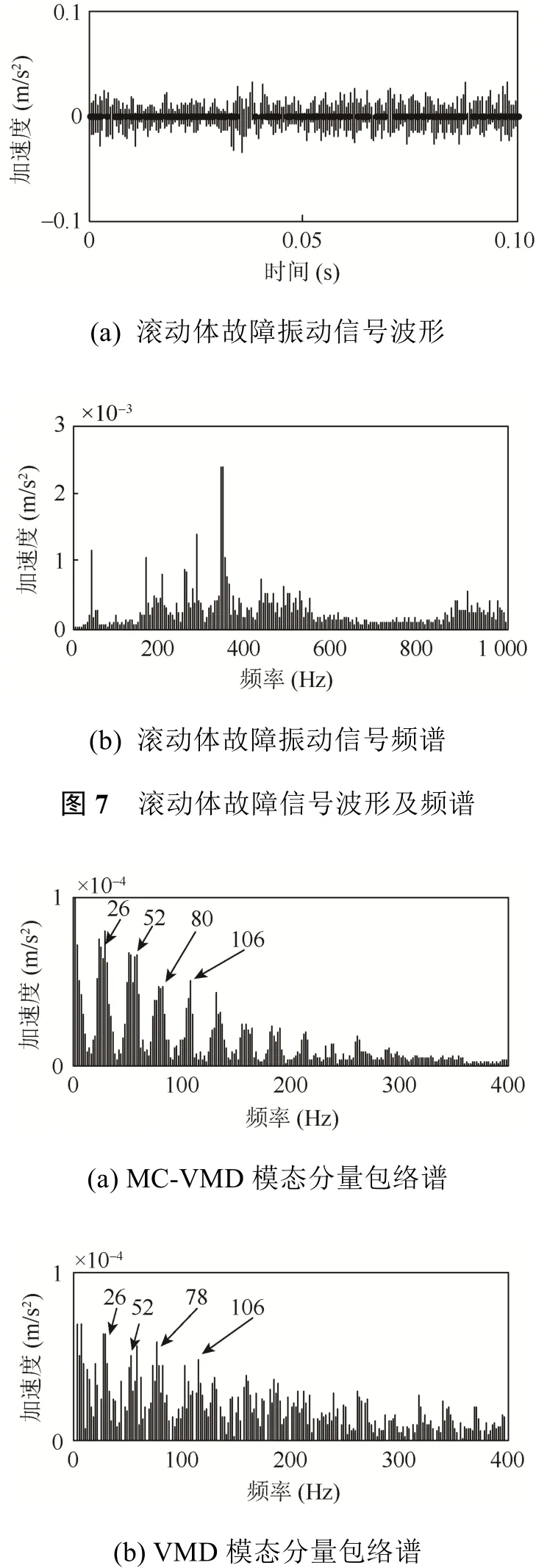
图8 滚动体故障诊断结果对比

4 结 论

通过滚动轴承故障诊断实例验证表明，采用基于多相关 VMD进行滚动轴承故障诊断是可行的。本文得到的主要结论有：

(1) 在滚动轴承早期微弱故障信号通常被强烈的背景噪声淹没，提取故障特征十分困难的情况下，基于MC-VMD的滚动轴承故障诊断方法能有效地提取出故障特征。

(2) 相比VMD分解方法，本文所提方法能够很好地消除了零均值噪声对特征信号的干扰，使特征信号凸显，有利于微弱特征信号的特征提取，通过仿真的故障轴承信号和滚动轴承实验进行了验证，结果证明了该方法的可行性和有效性。

[1] Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[2] 张志刚, 石晓辉, 施 全, 等. 基于改进EMD和谱峭度法滚动轴承故障特征提取[J]. 振动.测试与诊断, 2013, 33(3): 478-482,529-530.

[3] 朱文龙, 周建中, 肖 剑, 等. 独立分量分析-经验模态分解特征提取在水电机组振动信号中的应用[J].中国电机工程学报, 2013, 33(29): 95-101,14.

[4] 廖庆斌, 李舜酩, 辛江慧. 时序多相关-经验模式分解方法及其对车辆振动信号的分析[J]. 南京航空航天大学学报, 2007, 39(4): 465-470.

[5] 武 哲, 杨绍普, 刘永强. 基于多元经验模态分解的旋转机械早期故障诊断方法[J]. 仪器仪表学报, 2016, 37(2): 241-248.

[6] 周 智, 朱永生, 张优云, 等. 基于 EEMD和共振解调的滚动轴承自适应故障诊断[J]. 振动与冲击, 2013, 32(2): 76-80.

[7] Dragomiretskiy K, Zosso D. Variational mode decomposition [J]. Transactions on Signal Processing, 2013, 10(1109): 1-15.

[8] Mohanty, Gupta K K, Raju K S. Bearing fault analysis using variational mode decomposition [J]. International Conference on Industrial and Information Systems, 2014, 4(2): 1-6

[9] 武英杰, 甄成刚, 刘长良. 变分模态分解在风电机组故障诊断中的应用[J]. 机械传动, 2015, 39(10): 129-132.

[10] Muralidharan A, Sugumaran V, Soman K P, et al. Fault diagnosis of helical gear box using variational mode decomposition and random forest algorithm [J]. SDHM Structural Durability and Health Monitoring, 2015, 10(1): 55-80.

[11] 刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13): 3358-3365.

[12] 唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81.

Rolling Bearing Fault Feature Extraction Based on Improved Variational Mode Decomposition

Gao Hongwei1, Zhang Lirong2, Hou Shaojie1
(1. Economics and Business Computer Center, Hebei University, Shijiazhuang Hebei 050061, China; 2. Economics and Business Institute for Tourism Studies, Hebei University, Shijiazhuang Hebei 050061, China)

In order to solve the problems that the fault feature of rolling bearing in early failure period is difficult to extract, a method for fault diagnosis of rolling bearings based on multi-correlation variational mode decomposition (MC-VMD) was presented. First, vibration signal is jointly acquired through multiple acceleration sensors and the multi-correlation process is made for the signal in order to prominent fault signal characteristics. Then VMD was used to decompose the fault signal into several intrinsic mode functions (IMFs), and then the IMF of biggest related kurtosis was analyzed by the spectral kurtosis and envelope demodulation. Finally identify the working status and fault type of rolling bearings through envelope spectrum. The proposed method was applied to actual signals. The results show that this method enables accurate diagnosis of rolling bearing fault, the analysis results demonstrated the effectiveness of the proposed method.

multi-correlation; variational mode decomposition; rolling bearing; kurtosis criterion

TP 206.3；TH 133.33

10.11996/JG.j.2095-302X.2016060862

A

2095-302X(2016)06-0862-06

2016-04-26；定稿日期：2016-06-27

国家自然科学基金项目(51104052)

高红玮(1974−)，女，河北石家庄人，讲师，硕士。主要研究方向为计算机科学。E-mail：hongweigaolw@sina.cn

张丽荣(1973−)，女，河北石家庄人，讲师，硕士。主要研究方向为测试计量技术及仪器。E-mail：lizhang7303@sina.cn