仓储建筑运营荷载下地基固结的ABAQUS模拟分析

师旭超，李恒达

(1. 河南工业大学 土木建筑学院，河南 郑州450001；2.中国建筑第七工程局有限公司，河南 郑州 450004)

仓储建筑运营荷载下地基固结的ABAQUS模拟分析

师旭超1，李恒达2

(1. 河南工业大学 土木建筑学院，河南 郑州450001；2.中国建筑第七工程局有限公司，河南 郑州 450004)

粮油仓储设施地基在运营期内经受长期反复荷载的作用。该荷载不同于一般动力荷载，具有周期长、频率低等特性。基于修正剑桥模型，利用有限元软件，对低频正弦与梯形周期荷载作用下仓储设施地基的固结沉降特点进行了理论分析。通过对工程实例进行数值模拟分析，表明现场监测数据与其数值模拟结果具有较好的一致性。研究结果可为类似工程的地基基础设计提供参考。

反复荷载；软土地基；ABAQUS；数值模拟；修正剑桥模型

在筒仓和储罐类建筑的实际荷载中存在一些特殊的情况，由于结构传递给土体的反复荷载变化非常缓慢，不能被当做动力荷载来考虑。这种反复荷载是由筒仓或者储罐在填料及卸料的过程中产生的，它在填料期荷载递增，在卸料期荷载递减，而非瞬时加载和卸载。

基于太沙基理论，Wilson[1](1974)等根据矩形荷载公式，采用分段求解，得到了矩形反复荷载下饱和黏土的一维固结解答；Baligh[2]和Levadoux(1978)提出了一种基于分步周期加载情况下的解析解。Juran和Bernardet(1987)在固结试验中利用反压力描述周期加载再次发展了Baligh的理论。Rahal[3](1993)利用等效的正弦波载来代替Ca’Mello筒仓的实际荷载，对该筒仓沉降进行了理论分析。Soranzo在三角形周期加载中利用了此理论，并且被Favaretti和Mazzucato(1994)用来分析意大利的Ca’Mello筒仓在满载情况下的沉降；蔡袁强[4]、徐长节、狄刚[5](1998)利用固结微分方程的Laplace变换和循环波的Laplace变换，得出了多层土体下的一维固结理论的解析解；关山海、谢康和[6, 7]、胡安峰[8](2003)等利用分段函数形式，提出了低频梯形反复荷载下地基一维固结问题的解析解。然而在实际工程中，实际荷载需要通过拟合等效为相应类型的反复荷载。相关反复荷载方面的研究，较少有考虑弹塑性理论的固结性状及不同荷载类型的选取对沉降及孔隙水压力的影响。

本文基于正弦及梯形循环荷载下的固结理论及修正剑桥模型弹塑性理论，利用ABAQUS软件及其相关DLOAD子程序对长期反复荷载下的软土地基沉降进行分析，通过对数值模拟结果的分析，得出了一些重要结论，可为修建在软土地区的筒仓和储罐建筑的地基沉降预测提供参考。

1 修正剑桥模型

修正剑桥模型[9]是Burland 对Rose等人提出的剑桥模型的修正，因此称为修正剑桥模型(Modified cam-clay model)，是一种基于临界状态理论建立的弹塑性模型。该模型采用在主应力空间为椭圆形的屈服面(在p-q平面上的屈服轨迹为一半椭圆形)和相适应的流动法则，屈服方程为

(1)

其中

(2)

式中：p为有效平均正应力；q为有效偏应力；φ’为有效内摩擦角；p0为与塑性体积应变相关的变量。

在方程中有硬化参量的意义，取塑性体积应变为硬化参数，则硬化规律可表示为

(3)

式中：pa为初始应力，当前应力为零时取为前期固结压力，也可近似取为大气压力；ea为初始等向固结线在e轴上的截距；λ、κ分别为压缩指数与膨胀指数(回弹指数)。

在ABAQUS中，剑桥模型为Clay Plasticity模型[10]，它是在原有的剑桥模型的基础上做了扩展，其屈服函数的表达式采用了椭圆方程的函数表示，与常规的表达式有所不同，但本质是相同的，屈服函数为

(4)

式中：t为偏应力参数；β为控制屈服面形状的参数，硬化区屈服面在子午线平面上的投影；a为描述屈服面大小的参数，椭圆与临界状态线交点对应的p值(当β=1时，a值为p0/2)。

在Clay Plasticity模型中，ABAQUS提供了两种定义硬化规律的方式，一种是屈服面关于e0、λ、κ指数形式的硬化规律；另一种是上述体积塑性应变作为硬化参数的硬化规律，此种方式以表格的形式输入。

2 工程实例分析

2.1 工程地质条件

建造在高地下水位的软土地基上的某筒仓建筑，地质条件为较厚的黏土层，在计算深度内，有3层土体类别，相关试验参数见表 1。

表 1 土体参数表

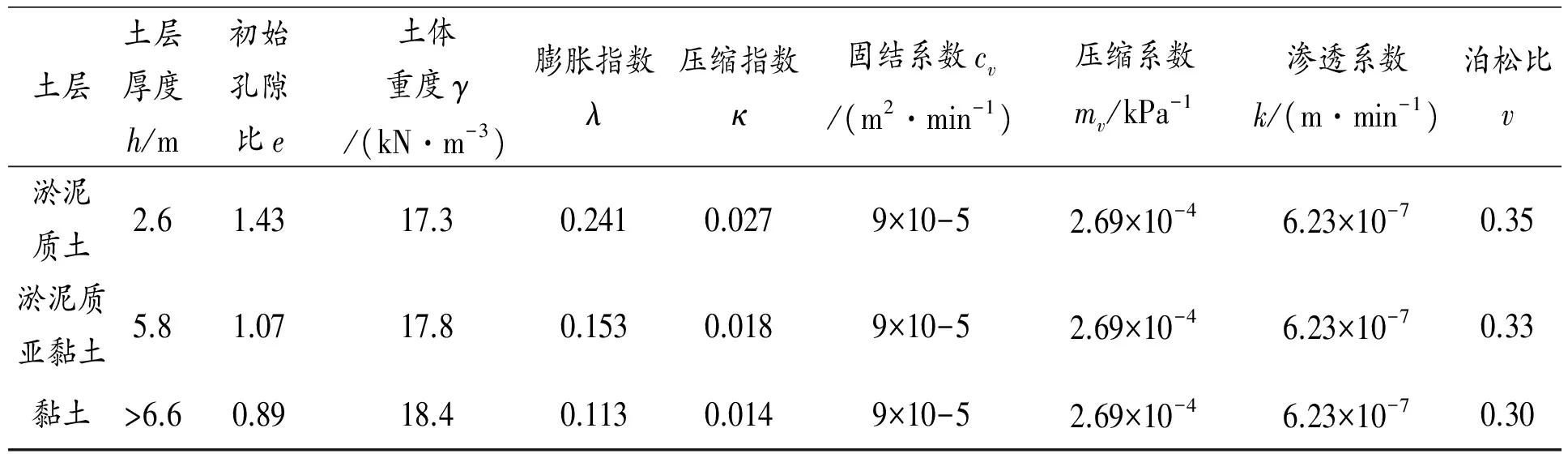
土层土层厚度h/m初始孔隙比e土体重度γ/(kN·m-3)膨胀指数λ压缩指数κ固结系数cv/(m2·min-1)压缩系数mv/kPa-1渗透系数k/(m·min-1)泊松比v淤泥质土2．61．4317．30．2410．0279×10-52．69×10-46．23×10-70．35淤泥质亚黏土5．81．0717．80．1530．0189×10-52．69×10-46．23×10-70．33黏土>6．60．8918．40．1130．0149×10-52．69×10-46．23×10-70．30

2.2 荷载分析及计算模型的建立

筒仓受荷是典型的低频反复荷载，本文拟研究的实际荷载类型为非同一固定的梯形反复荷载，而是不规则的，大致与梯形荷载有相近的荷载形状。为便于数值分析，将实际荷载等效为一致的荷载，ABAQUS输出的荷载图如图1所示。筒仓的取存周转周期为1 a，梯形荷载加载系数为α=0.384 6，β=1.333 3，设筒仓初始自重应力为10 kPa，最大荷载为40 kPa，土层的先期固结压力为10 kPa。分析周期为4 a。正弦荷载假定周期为T=1 a，角速度为2π/T，幅值为30 kPa。依据上面条件，通过ABAQUS有限元软件提供的DLOAD荷载子程序，并根据循环荷载公式编制相应的等效荷载，导入程序进行分析，并通过UVARM用户自定义场输出变量，输出需要的场变量，从而提高绘图的高效性。最后分析筒仓投产4 a周期内，在两种等效反复荷载及实际荷载作用下的地基沉降量及超静孔隙水压力的变化规律。

计算模型简图如图 2所示，取土体深度15 m为模拟计算模型，取宽度为5 m建立平面模型，模型材料为土，考虑渗流与固结的耦合，故选择孔隙流体/应力(CPE8RP)单元类型，土体上表面或下表面排水。采用修正剑桥模型进行分析，相关模型参数由表格选取。

3 模拟及计算结果分析

3.1 基础沉降

筒仓底部地基沉降曲线如图3所示，图中正弦反复荷载的沉降值较另外两者偏小。可以看出，由于等效梯形反复荷载与实际荷载有较高的相似性，故两者模拟结果非常接近，在以后的3 a中沉降量较小，并逐渐趋于缓慢增加的状态。

由计算结果可知，单面排水条件下，等效梯形荷载的模拟值为125 mm，正弦荷载的模拟值为116 mm；双面排水条件下，等效梯形荷载的模拟值为131 mm，正弦荷载的模拟值为126 mm。实际最大沉降为131 mm。各结果之间存在一定差异，但并不明显。

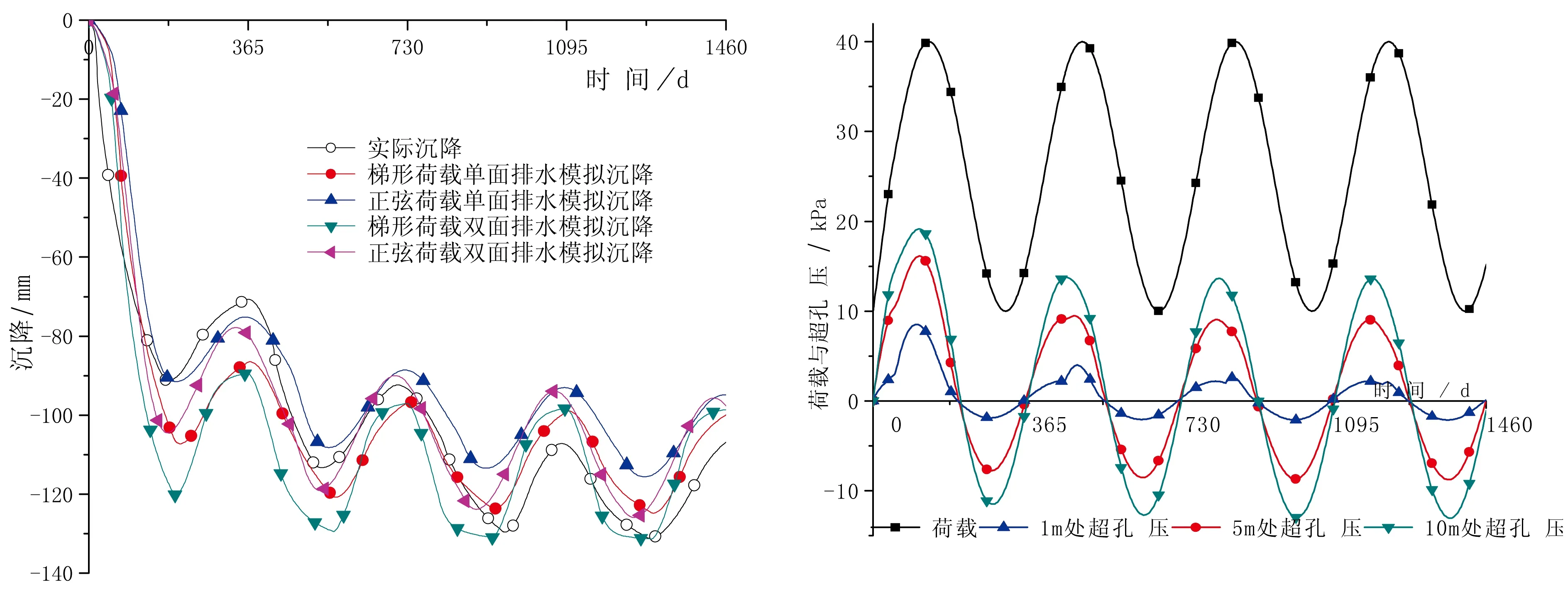
图3 荷载—沉降曲线 图4 正弦荷载、超孔压—时间变化曲线

由图3可以看出，实际荷载和等效梯形反复荷载作用下，ABAQUS模拟的地基沉降与荷载的变化有相同的发展规律。实际沉降的变化与ABAQUS的模拟值有较好的一致性。单面排水条件下的总体沉降速率较双面排水条件慢，特别是在第一个荷载周期沉降量都较大，随后各周期的沉降变化基本稳定。

3.2 超孔隙水压力分析

某深度处正弦荷载下的荷载孔压变化曲线如图4所示，在土层较深处，正弦荷载的超孔隙水压力变化大致也呈现为正弦曲线形式，但超孔压的变化要先于荷载的变化。由图4可以看出，前两个循环最大值在荷载峰值较近处，随着加载次数的增加，孔压的最大值逐渐转移到荷载峰值之前。这种变化的主要原因是正弦荷载加载速率在达到峰值之前急剧减小引起的。速率减小较大处与峰值处的时间差，由有限元计算结果知，两者曲线的相位角差值约为41.51°，相差时间为42.08 d。

4 结论

通过对反复荷载作用下筒仓地基沉降的模拟对比，可以得到以下结论：

(1)在选择荷载方面应考虑多方面因素，拟合一个与实际相近的荷载类型，进行地基沉降预测。选择不同的边界条件对分析结果也有一定影响。

(2)正弦荷载下的沉降曲线变化滞后于荷载的变化，而超孔隙水压力的变化超前于荷载的变化。

[1] Wilson N, Elgohary M. Consolidation of soils under cyclic loading[J]. Canadian Geotechnical Journal, 1974, 11(3): 420-423.

[2] Balighm M, Levadoux J. Consolidation theory of cyclic loading[J]. Journal of Geotechnical Engineering Division ASCE, 1978, 104(4): 415-431.

[3] Rahal M A, Vuez A R. Analysis of Settlement and Pore Pressure Induced by Cyclic loading of Soil[J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE, 1998, 124(12): 1208-1210.

[4]蔡袁强, 徐长节, 袁海明. 任意荷载下成层黏弹性地基的一维固结[J]. 应用数学和力学, 2001, 22(3): 307-313.

[5]蔡袁强, 徐长节，丁狄刚. 循环荷载下成层饱水地基的一维固结[J].振动工程学报, 1998, 11(2): 184-193.

[6]谢康和, 周瑾, 董亚钦. 循环荷载作用下地基一维非线性固结解析解[J]. 岩石力学与工程学报, 2006, 25(1): 21-26.

[7]谢康和, 郑辉, 李冰河. 变荷载下成层地基一维非线性固结分析[J]. 浙江大学学报: 工学版, 2003, 37(4): 426-431.

[8]关山海, 谢康和, 胡安峰. 低频循环荷载下地基一维固结性状分析[J]. 岩土力学, 2003, 24(5): 849-853.

[9]殷宗泽. 土工原理[M]. 北京: 中国水利水电出版社, 2007.

[10]费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2009.

ABAQUS simulation analysis on consolidation of silo buildings' foundation in operational period

SHI Xu-chao1, LI Heng-da2

(1.SchoolofCivilEngineeringandArchitecture,HenanUniversityofTechnology,Zhengzhou450001,China; 2.ChinaConstructionSeventhEngineeringDivision.CORP.LTD,Zhengzhou450004,China)

Silos and oil tanks are filled and emptied periodically in operational period, which is a typical case of soft soil layer under long-term cyclic loading. In most cases, this kind of loading has a long-time cycle and low frequency, which can't be regarded as dynamic loading. This paper is based on the theory of consolidation between low-frequency sinusoidal and trapezoidal cyclic loading as well as Modified Cam-clay model constitutive equation. With the use of the software of ABAQUS, the long term settlements caused by cyclic sinusoidal and trapezoidal loading during service period are theoretically studied. Through the analysis at numerical simulation of the equivalent cyclic sinusoidal and trapezoidal loading to a silo, as it shows, the result of this theoretical computation is in coherence with the result of numerical simulation. And the conclusion is significant for foundation design.

repeated loading; soft soil foundation; ABAQUS; numerical simulation ; Modified Cam-clay model

2016-06-20

国家自然科学基金(U1304526)

师旭超(1973—)，男，河北邯郸人，博士，教授。

1674-7046(2016)06-0007-04

10.14140/j.cnki.hncjxb.2016.06.002

TU433

A