一类行列式考研题目的算法探究
郭 杰,郭淑妹
(信息工程大学 理学院,河南 郑州450001)
一类行列式考研题目的算法探究
郭 杰,郭淑妹
(信息工程大学 理学院,河南 郑州450001)
结合线性代数中常用的“打洞”技巧,对具有某种特定结构的行列式提出了具有针对性的计算方法.计算方法思路清晰,简洁高效,对这种类型的行列式的计算起到事半功倍的效果.
线性代数;行列式计算;考研试题;“打洞”技巧;矩阵初等变换
0 引言
行列式是线性代数[1-3]的开篇章节,对于学生领悟线性代数的思想和方法有着重要意义,行列式的熟练掌握对于后面章节的学习起着举足轻重的作用,但是学生往往对行列式的计算又有些不知所措、无从下手.行列式计算不理想的原因是多方面的,一方面,行列式的定义抽象、不可捉摸,对于刚入学的大一新生来说是个不小的挑战;另一方面,行列式的题目千变万化、纷繁复杂,学生不可能把每个题目都做一遍.因此引导学生学会归纳整理则会事半功倍,对于具有某种特点的行列式就用某种固定的解法,针对性强,提高做题效率.对该类题目的做法要理解其要点,举一反三、触类旁通.
行列式是研究生入学考试的必考知识点.从历年真题来看,行列式在考研数学试卷中一般以填空题、选择题为主,所占比例不是很大,但却是必考内容,而且不只是考察行列式的概念、性质、运算,与行列式有关的考题也不少,例如方阵的行列式、求逆矩阵、向量组的线性相关性、矩阵的秩、线性方程组、方阵的特征值、正定二次型、正定矩阵等都会涉及行列式.如果试卷中没有独立的行列式试题,必然会在其他章节的试题中得以体现,所以在教学中必须要求学生熟练掌握行列式计算的常用方法.
1 行列式计算的一般方法介绍
行列式的计算方法有很多,比如降阶法,有时与递推法结合使用,或者借助特殊行列式比如三角行列式、范德蒙行列式、三线型行列式等,还有一些较高难度的加边法、拆分法等.行列式计算的题型一般分为数字型行列式的计算、抽象型行列式的计算、含参数的行列式的计算.下面我们就一类行列式关于考研题目的计算进行探究.
例1 2015年研究生考试数学(一)中的填空题第13题[4-5],计算行列式
解法1 从行列式的结构上看,特点明显,大多数元素为零,同时元素分布比较有规律,因此可以设法找出n阶行列式Dn与较低阶行列式的关系,以此类推来计算行列式.据此,按行按列展开,然后结合递推法计算.对行列式Dn按第n行展开有
整理得Dn=Dn-1+2n,进一步有
Dn-1=Dn-2+2n-1
Dn-2=Dn-3+2n-2,
…
D2=D1+22,
D1=2,
相加求和得Dn=2n+2n-1+…+22+2=2n+1-2.

以上两种方法是计算行列式的常用的基本方法,对于大多数行列式来说,应用上述方法均可求解.但是具有这种特定结构的行列式,我们还可以采用更有针对性的解法,做到有的放矢,精简高效.
2 特定结构行列式的针对性解法
为了探究计算这一类行列式的一般解法,需要介绍下述的舒尔公式,通常又称为矩阵“打洞”技巧,实际上是将矩阵的初等变换推广到对分块矩阵施行初等变换,华罗庚教授形象地称此方法为矩阵“打洞”.矩阵“打洞”技巧在行列式计算、可逆阵的判定、逆矩阵的求解、二次型理论等方面的应用,显示了它是矩阵计算中最基本的技巧,也是最重要、 最有用的技巧.



证明思路也很简单,就是利用子矩阵A或者D的可逆性来“打洞”,换句话说就是将子矩阵B或C化为零子块.总之“打洞”并不复杂,就是利用可逆的子矩阵来做初等变换消去其他的子矩阵,从而实现问题的简化.
解法3 令

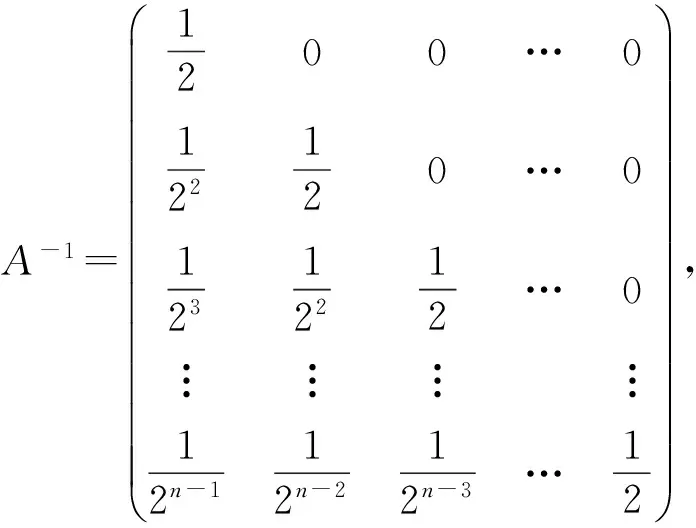
同样,我们可以用舒尔公式简化线性代数教材中的习题.

证明令

注意:题中约定x≠0,若x=0,可用第1列展开得证.
考研题目纵有千变万化,但是万变不离其宗,比如2016年考研试题数学一的填空题第13题:
不难看出,这个行列式和例2的结构完全相同,只是阶数降了,改编为四阶行列式.这个类型的行列式计算技巧掌握了,不论如何变形,我们都能顺利求解.同时,我们还可以利用舒尔公式2)计算这类型的行列式考研题目.
解令
以上借助矩阵的“打洞”技巧计算了一类具有某种特点的行列式,给出了具体的操作方法和步骤,希望能够引导读者对行列式计算更进一步的探索.
[1]同济大学数学系.线性代数[M].5版.北京:高等教育出版社,2007:1-28.
[2]魏战线,李继成.线性代数与解析几何[M].2版,北京:高等教育出版社,2010:1-27.
[3]方文波,段汕,江世宏,等.线性代数及其应用[M].北京:高等教育出版社,2011:6-35.
[4]祝清顺,马朝忠,张宁.线性代数疑难释疑[M].浙江:浙江大学出版社,2013:1-56.
[5]李国重,杜院录,祝清顺.线性代数课程教学执行计划[M].上海:上海交通大学出版社,2013:1-32.
[6]孟道骥,王立云.打洞技巧[J].高等数学研究,2006,9(4):15-20.
Exploration on Determinant of Grind Subject Algorithm
GUO Jie,GUO Shumei
(SchoolofScience,InformationEngineeringUniversity,Zhengzhou450001,China)
Based on skills of making a hole in linear algebra,corresponding algorithm for a particular structure of determinant is proposed.The method is clear,concise and very efficient for this type of determinant calculation.
linear algebra; determinant calculation; questions of postgraduate entrance exam; skills of making a hole; elementary transformation of matrix
2016-08-12
信息工程大学教育教学项目(XDJY3-2016039,XD6201513C)
郭 杰(1979—),女,河南淮阳人,信息工程大学理学院副教授,主要研究方向:统计学应用及数据处理.
10.3969/j.issn.1007-0834.2016.04.012
G642.0;O151
1007-0834(2016)04-0048-04

