大型气浮沉箱拖航过程中的垂荡运动特性分析

丁红岩，朱 岩，张浦阳，乐丛欢，韩彦青

（1．天津大学水利工程仿真与安全国家重点实验室，天津300072；2．天津大学滨海土木工程结构与安全教育部重点实验室，天津300072；3．天津大学建筑工程学院，天津300072）

大型气浮沉箱拖航过程中的垂荡运动特性分析

丁红岩1，2，3，朱 岩3，张浦阳1，2，3，乐丛欢1，韩彦青3

（1．天津大学水利工程仿真与安全国家重点实验室，天津300072；2．天津大学滨海土木工程结构与安全教育部重点实验室，天津300072；3．天津大学建筑工程学院，天津300072）

为防止大型气浮沉箱在浅水海域拖航中由于垂荡值过大造成触底，本文研究了气浮沉箱的垂荡运动特性。采用MOSES分析软件获得气浮沉箱在不规则波波浪下垂荡位移的响应，经Welch法分析得到气浮沉箱的固有垂荡周期；利用周期不同的规则波浪进行气浮沉箱拖航模拟，以此获得相应的垂荡运动位移幅值最大点对应的周期值范围。同时，分析了理论垂荡固有周期值的计算过程，并研究了不同吃水对气浮沉箱垂荡运动特性的影响。证明经过MOSES分析软件和功率谱估计得到的垂荡固有周期值是合理的，可以参与水动力学计算并作为选取附加质量因素时的参考值；随着吃水的加大或分舱内气压的减小，垂荡固有周期值有增大的趋势。

气浮沉箱；固有垂荡周期；附加质量因素；垂荡；拖航；波浪

气浮沉箱基础海洋平台适于沉箱式人工岛的主体建设，并在浅海和沼泽地油气田勘探和开发中得到了迅速发展和广泛应用。气浮沉箱基础海洋平台是无底结构，通过气浮的方式来进行拖航运输，拖航时气浮沉箱基础顶端封闭，通过向箱中充入空气，排开水体，产生浮力。因此气浮结构可以通过提高充气量来快速减小结构的整体吃水，从而避免大型海洋结构在浅水海域拖航时触底现象的产生，这也是发展气浮结构的原因之一。气浮结构与传统海洋结构型式受力机理不同:传统的海洋结构为实浮体，即刚性结构支撑在水弹簧之上；而气浮式结构则为刚性结构支撑在水弹簧与气弹簧的耦合弹簧之上。水弹簧与气弹簧串联后的弹性刚度将小于独立的水弹簧弹性刚度，在相同的下沉位移量下气浮体的抗力（矩）小于通常实浮体的抗力（矩），即稳性较一般传统海洋结构要差。同时，气浮体结构自由垂荡与摇摆运动的固有频率也比实浮体结构的固有频率低，在拖航过程中，可能会在波浪等环境荷载作用下产生较大的动力效应。尤其在气浮体的垂荡稳定和运动特性上必须从气浮结构的受力特性着手来进行分析。目前国内外关于结构气浮的垂荡运动研究非常少，丁红岩、刘宪庆、B．Chenu、M．T．Morris-Thomas、Pantouvakis J P等对结构气浮的各项运动特性进行了一些探索性研究［1-4］，刘宪庆［1］等以箱型气浮结构为例，通过气体绝热方程，考虑气体的压缩性，对气-水交界面处的非线性边界条件进行了推导。丁红岩等［2］主要研究了气浮筒型基础在不同海况下进行拖航时，不同变量因素对筒型基础各项运动特性的影响及响应。但上述文章试验中均采用筒结构试验模型来进行分析，对于大型沉箱是否合理，还需进一步验证。B．Chenu等［3］外国学者在对气浮混凝土结构进行研究后得到了气浮体相对实浮体稳性要差以及气浮结构通过增加分舱数可相应提高稳性的实验结论。为保证拖航中气浮沉箱结构不因垂荡值过大而产生触底现象。根据共振效应原理，可通过避免沉箱在接近其固有周期的波浪下进行拖航。对气浮沉箱结构的拖航垂荡运动特性应进行专门的研究和分析。在国内外学者对不同气浮结构的拖航过程中结构的运动响应特性研究的基础上，本文针对气浮沉箱基础平台的拖航，先采用水动力学软件MOSES进行了数值模拟分析，再针对得到的垂荡运动响应数值模拟结果，创新性的使用了Welch［5］功率谱估计法进行了估计分析。

1 气浮结构理论模型

1．1 气浮沉箱动力学计算理论

MOSES对动力学问题处理基于结构运动是微小的；流体是无粘性和无旋的；结构的变形加速度忽略不计；水、结构的相互作用力与结构的变形相互独立这四个基本假设。在这些简化条件下，结构的运动方程可表示为

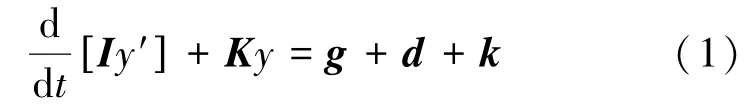
式中:y为浮体结构外形参数，I为惯性矩阵，K为刚度矩阵，d为重力，k为结构上其他作用力。g为水和结构的相互作用力，在MOSES中通过对浸没在水中的结构表面压力积分得到，表面压力可以通过线性化的伯努利方程得到:

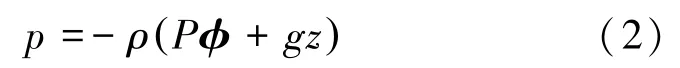
式中:ρ为流体的密度，g为重力加速度，z为淹没的淹湿深度，φ为流体的速度势。φ满足的条件如下所示

将物体的速度势分解为式（6）的形式:

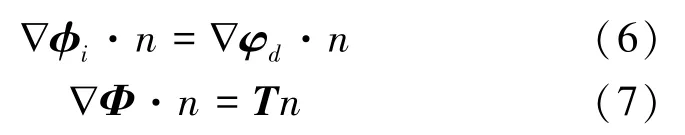
式中:φi为入射势；φd为绕射势；Φ为幅射势；T是将参考点的速度转化到结构表面每一点速度的矩阵。

作用在浮体上的作用力为

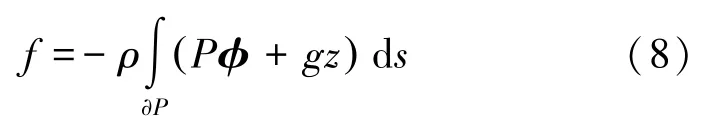
1．2 气浮平衡理论

MOSES中对于气浮结构的模拟是通过内置的＆COMPARTMENT命令及其各相应选项来完成的［6］。-OPEN_VALVE选项将各分舱底部打开，通过-PERCENT选项设置开口舱内的初始充水量，通过-INT_PRE选项设置内部初始气压及内部初始气体百分量。气浮结构的平衡条件可以表示为

式中:G为结构的自重，V0为结构排水体积，P0为内部气压和大气压力的差值，A0为气压作用的表面积。

1．3 Welch功率谱估计

功率谱估计采用Welch法，功率谱估计为

式中:w( n)为窗函数，本文选用Rectangular窗函数，0≤n≤N-1时w( n)=1，其他情况w( n)=0。因该窗主瓣宽度比较窄，能精确读出主瓣频率，且分辨率高，适于测定振动物体的自振频率，且该函数在分析时易于理解和计算［7-8］。

2 气浮沉箱拖航模拟

2．1 结构模型

模型尺寸如图1所示，为混凝土结构，模型总长75 m，宽49 m，高26．5 m。总体结构分为两层:上层为密闭矩形空间结构，高度为23．5 m；底层为裙板结构，高度为3 m。在底层设置了70个高度为3 m，平面尺寸为7．5 m×7．0 m的底部开口分舱来保证结构的总体强度及气浮稳性。分舱数目的增加可以在一定程度上改善气浮沉箱的稳性［9］。在MOSES中，不考虑气浮沉箱的材料及内部具体构造，仅对结构体外表面按照具体尺寸进行建模，整个模型结构被设置成一个封闭的多面壳体。模型的质量力按加载于结构体质心处进行考虑。建模的原点取在底面的矩形的几何形心上，x轴为沉箱航行方向，z轴方向背离海平面向上，y轴方向按右手定则确定，重心位置为（0，0，14．82），三个方向的惯量半径为（15．93，22．67，26．01），结构总重为34 440．3 t。其中结构的重心位置和结构的重量是从结构设计过程中的模型中提取的精确数值。惯性半径的精确计算方法为

式中:I为转动惯量，m为质量。在实际的计算过程中，MOSES给出一般船舶的惯性半径简便近似计算方法。本部分计算即为此方法求得。

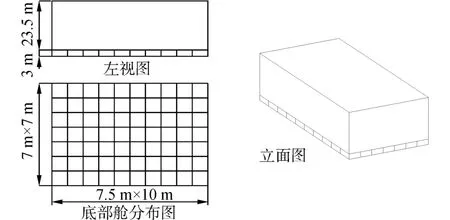
图1 模型尺寸Fig．1 Dimensions of model

2．2 拖航模型

模拟的水深与沉箱实际拖航时的水深一致，为10 m，水域范围为无限大，模型系揽点的坐标为（37．50，0，10．58），沉箱初始吃水为10．58 m，底部的群舱中水封高度为1．44 m，初始气压为191 811．3 Pa；不规则波谱为ISSC类型，模拟方法采用MOSES内置命令＆ENV及其命令选项-SEA完成［6］。按表1所列不规则波海况进行拖航模拟，并在此基础上增设16组规则波海况进行模拟验证。规则波仅改变周期，其他条件和不规则波保持一致（波高1 m、风速6 m、航速4 kn、迎浪），周期从1～16 s依次增大。

表1 数值模拟拖航条件Table 1 Towing conditions of numerical simulation

使用MOSES建立沉箱海洋拖航模型，由于MOSES中的时域分析不能考虑航速的影响，因而利用揽绳将模型系在固定不动的拖船上，施加与拖航速度大小相同方向相反的海流来考虑航速的影响［10-11］。拖航模型如图2所示。

图2 拖航模拟图Fig．2 Simulation of towing

3 沉箱的数值模拟结果分析

通过对气浮沉箱原型的拖航进行数值模拟，能较为方便的获得沉箱在不同拖航条件下的垂荡运动特性。本文分析了不同周期的不规则波、规则波下的沉箱的垂荡位移，经Welch运算获得了其固有垂荡周期值，并进行了该固有周期值可行性的验证，以及研究了气浮式结构固有垂荡周期的理论计算过程。并通过调节沉箱的吃水计算了结构在不同吃水下的垂荡固有周期。

3．1 不规则波波浪下垂荡运动响应

模拟是在随机选择一个不规则波浪海况条件下，对沉箱原型进行的数值模拟。拖航条件参见表1。不规则波下的沉箱垂荡位移运动曲线如图3～5所示。

分析不同平均周期下沉箱的垂荡位移值可知，在平均周期值为7．0 s时，沉箱的垂荡位移幅值的整体变化幅度要大于沉箱在平均周期值为3 s和11 s的垂荡位移的变化幅度，而且垂荡位移的峰值也最大。在不规则波2的条件下，垂荡位移值很小，几乎没有明显变化。可见波浪的运动周期值的大小会对沉箱的垂荡运动造成影响，影响效应随周期值增加呈中间大，两头小的变化趋势。

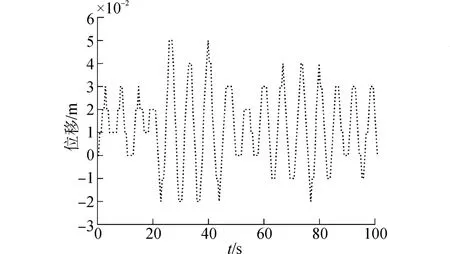
图3 不规则波1下的沉箱垂荡运动曲线Fig．3 Vertical motion carves of the caisson in Irr-1

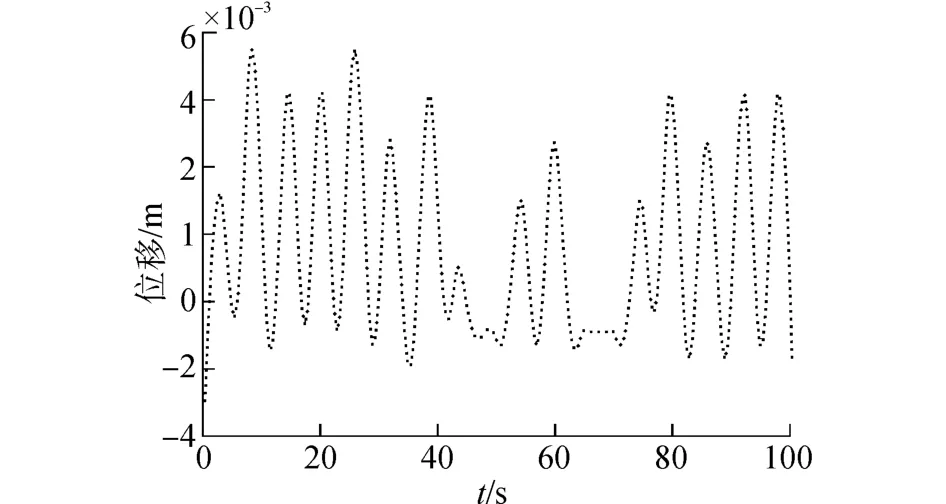
图4 不规则波2下的沉箱垂荡运动曲线Fig．4 Vertical motion carves of the caisson in Irr-2

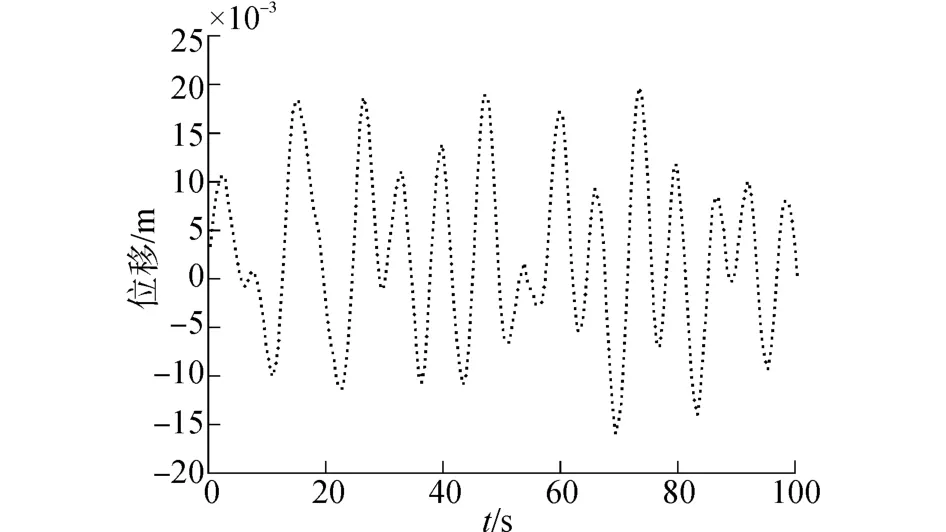
图5 不规则波3下的沉箱垂荡运动曲线Fig．5 Vertical motion carves of the caisson in Irr-3

3．2 功率谱

对得到的垂荡位移运动数据通过运用Welch法进行功率谱估计分析，以此获得的沉箱垂荡位移的功率谱估计如图6所示。可在曲线上获得功率最大值对应的频率值f1=0．152 63，得到

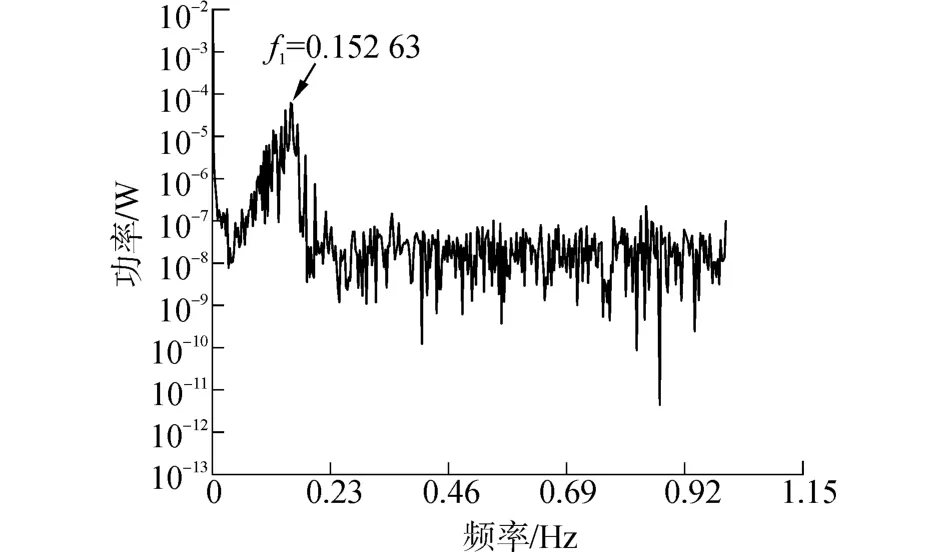
图6 不规则波1下沉箱的功率谱曲线Fig．6 Power spectrum carves of the caisson in Irr-1

对不规则波条件2、3进行模拟，分别得到功率谱如图7所示，相应频率值f2=0．152 63、f3= 0．155 26。与上文分析结果相一致，说明用此频率值作为相应沉箱固有垂荡频率是可行的。并取上述倒数的平均值作为固有周期值Tz=6．55 s。

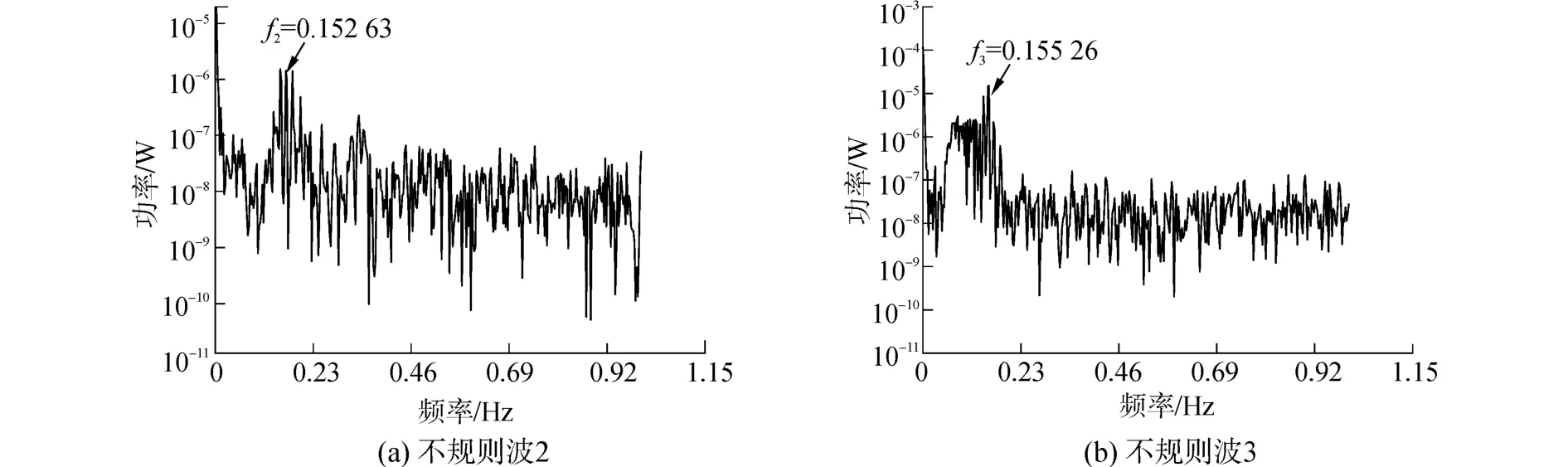
图7 不规则波2、3下的沉箱的功率谱曲线Fig．7 Power spectrum carves of the caisson in Irr-2＆3

3．3 规则波浪下垂荡运动响应

通过模拟得到了沉箱在不同周期规则波下拖航时的垂荡运动位移振幅值，位移振幅值随周期的分布如图8所示。

根据位移幅值的分布规律，从图8（a）中可以观察到沉箱垂荡位移振幅在周期为6～7的范围内会达到最大值。增加周期为6．4 s和6．6 s的两组规则波并进行模拟，得到振幅值分布图8（b），可以观察到幅值相对原来的规则波均有很大增加，这与上文中得到的沉箱垂荡固有周期值Tz=6．55 s相吻合。表明前述所得的垂荡周期固有值是合理的。

3．4 附加质量因素的计算

垂荡周期理论值的计算:忽略水阻尼影响，根据动力学理论，单自由度气浮结构垂荡运动的固有周期为

式中:msw为气浮结构做垂荡运动是结构体系的质量，包括结构自身质量和随结构运动的水体质量；Kbz为气浮恢复力刚度系数［12］。

式（12）中的msw包括结构自身质量ms和随结构运动的水体质量mw，记为

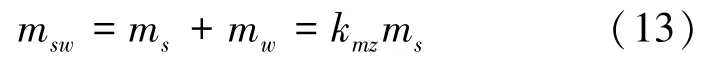
式中:kmz为气浮结构垂荡运动的附加质量因素。在船舶动力学中，垂荡和摇摆运动的附加质量因素kmz和kmx均建议取为1．2，但船舶为实浮体结构，取该值是否合理需要经过模拟验证。本次数值模拟得到了该沉箱气浮结构的垂荡周期Tz，则根据式（12）有

这样就可以通过数值模拟来测算沉箱气浮结构作垂荡运动的附加质量因素。或对该气浮沉箱经建议kmz算得垂荡固有周期值T，与通过功率谱得到的周期值Tz进行比较，从而判定建议附加质量因素的合理性。经计算该结构的T=6．79 s，与Tz的相对误差约为4％。

3．5 不同吃水对沉箱垂荡运动的影响

波浪高度对气浮体结构的各项运动特性均有较大影响［13-14］，本文在模拟中还分析了不同吃水对沉箱拖航垂荡运动的影响，如图9所示。

从图9中可以看出沉箱垂荡的固有频率值随着吃水的增加呈左移趋势。这是由MOSES中对于吃水的调整是通过调整分舱内部的气水比进行的，在沉箱重量不变的前提下，吃水增加，分舱内部气压变小，气弹簧的刚度也变小，而内部水弹簧的刚度保持不变，导致沉箱的总体刚度降低，沉箱垂荡频率降低。

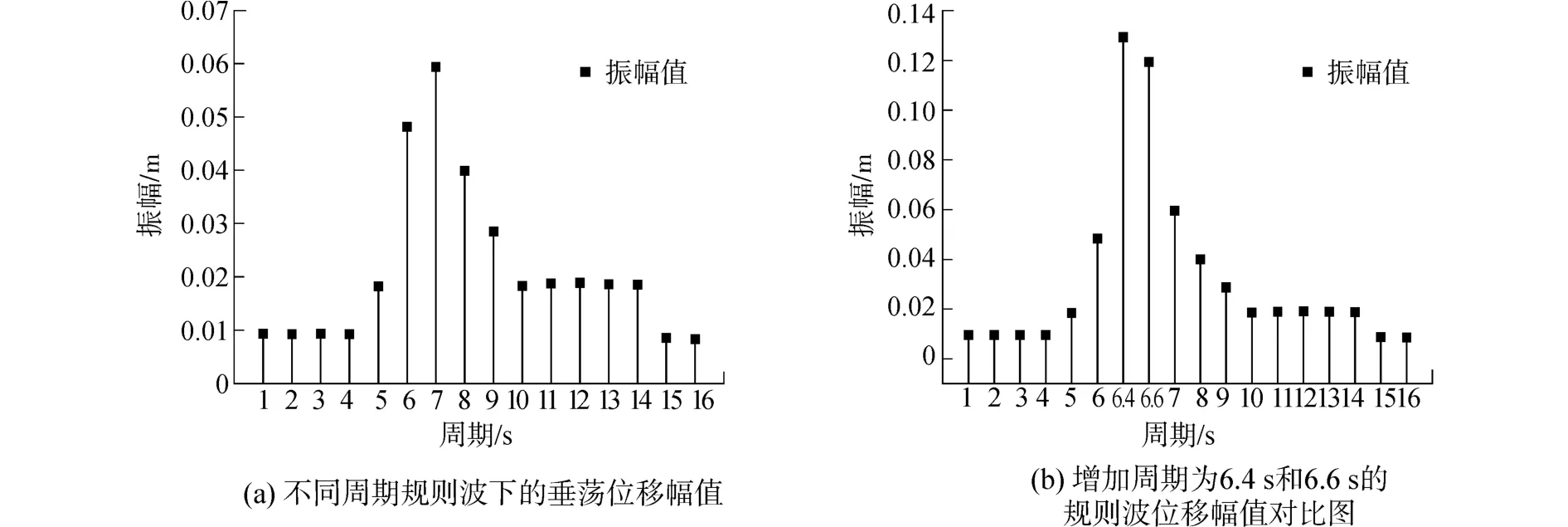
图8 规则波下的沉箱的位移振幅值统计垂线图Fig．8 Statistic carves of the caisson displacement amplitude values in regular waves

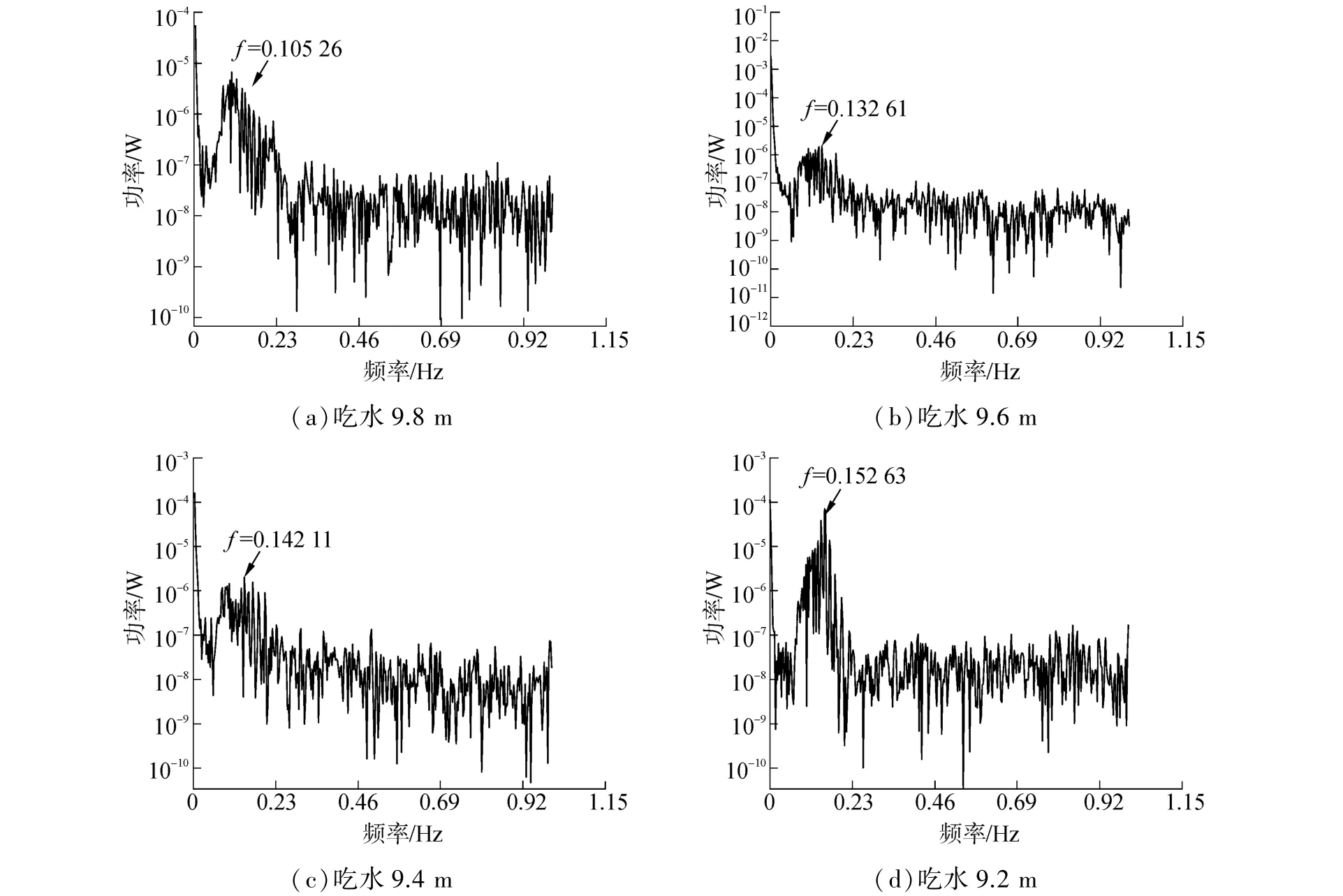
图9 不同吃水对沉箱的垂荡周期值得影响Fig．9 Influence of different drafts on the caisson heave period

上述气浮沉箱在不同吃水下其垂荡固有频率变化的趋势，为气浮沉箱在拖航时提供了一种快速改善垂荡运动的方法。可以通过调节气浮沉箱的气压来相应改变整体结构的垂荡固有周期值，来减小垂荡的位移值，保证结构的安全。

4 结论

通过MOSES分析软件对沉箱拖航进行数值模拟可以很好地对沉箱原型拖航运动进行分析，能方便地通过海况条件各项参数（如波浪条件、风速）的变化，来实时模拟各种海域条件，并得到沉箱原型结构在不同海况下运动的响应情况以及各种因素的变化对沉箱原型结构各项运动特性的影响情况，为分析沉箱拖航提供参考。得到以下主要结论:

1）使用MOSES软件和Welch功率谱估计分析得到沉箱拖航时合理的垂荡固有周期是可行的。

2）数值模拟得到的垂荡固有周期值可以作为选用船舶规范建议附加质量因素的参考值。

3）吃水的不同会影响沉箱的垂荡固有频率，且随着吃水的增加或降低，频率值呈相反的趋势变化。因而可以通过调节气浮沉箱的气压来改变沉箱的垂荡固有周期值，来应对突发的海况条件并相应减小垂荡位移值。

［1］刘宪庆，辜文杰，别明娟，等．箱型气浮结构的垂荡水动力系数解析研究［J］．应用力学学报，2015，32（6）: 1012-1018．LIU Xianqing，GU Wenjie，BIE Mingjuan，et al．Analytical solutions of hydrodynamic coefficient for heave motion by an air-floating rectangular box［J］．Chinese journal of applied mechanics，2015，32（6）:1012-1018．

［2］丁红岩，石建超，张浦阳，等．气浮筒型基础结构垂荡水动力系数研究［J］．中国海洋大学学报:自然科学版，2015，45（12）:113-118．DING Hongyan，SHI Jianchao，ZHANG Puyang，et al．Study on heaving hydrodynamic coefficient of air-floating bucket foundation［J］．Periodical of Ocean University of China:Natural Science Edition，2015，45（12）:113-118．

［3］CHENU B，MORRIS-THOMAS M T，THIAGARAJAN K P．Some hydrodynamic characteristics of an air-cushion supported concrete gravity structure［C］／／Proceedings of the 15th Australasian Fluid Mechanics Conference．Sydney，Australia:The University of Sydney，2004．

［4］PANTOUVAKIS J P，PANAS A．Computer simulation and analysis framework for floating caisson construction operations［J］．Automation in construction，2013，36:196-207．

［5］GUPTA H R，BATAN S，MEHRA R．Power spectrum estimation using Welch method for various window techniques［J］．International journal of scientific research engineering＆technology，2013，2（6）:389-392．

［6］Ultramarine，Inc．Reference manual for moses［CP］．Ultramarine，Inc．，2009．http:／／www．ultramarine．com／hdesk／document／ref_man．htm．

［7］SHEIKH S A，MAJOKA A Z，REHMAN K U，et al．Nonparametric spectral estimation technique to estimate dominant frequency for atrial fibrillation detection［J］．Journal of signal and information processing，2015，6（4）:266-276．

［8］UMEBAYASHI K，TAKAGI R，IOROI N，et al．Duty cycle and noise floor estimation with Welch FFT for spectrum usage measurements［C］／／Proceedings of the 2014 9th International Conference on Cognitive Radio Oriented Wireless Networks and Communications（CROWNCOM）．Oulu，Finland:IEEE，2014:73-78．

［9］陈浩，张亮．漂浮式潮流电站载体水动力性能分析［J］．应用科技，2014，41（1）:65-68．CHEN Hao，ZHANG Liang．Hydrodynamic performance analysis of floating current power station［J］．Applied science and technology，2014，41（1）:65-68．

［10］丁红岩，黄旭，张浦阳，等．筒型基础平台气浮拖航的影响因素分析［J］．工程力学，2012，29（10）:193-198．DING Hongyan，HUANG Xu，ZHANG Puyang，et al．A-nalysis on influence factors of towing of air float bucket foundation platform［J］．Engineering mechanics，2012，29（10）:193-198．

［11］ZHANG Puyang，DING Hongyan，LE Conghuan．Hydrodynamic motion of a large prestressed concrete bucket foundation for offshore wind turbines［J］．Journal of renewable and sustainable energy，2013，5（6）:063126．

［12］别社安，时忠民，王翎羽．气浮结构的运动特性研究［J］．中国港湾建设，2001（2）:18-21，25．BIE She’an，SHI Zhongmin，WANG Lingyu．Study on kinetic properties of air float structures［J］．China harbour engineering，2001（2）:18-21，25．

［13］THIAGARAJAN K P，MORRIS-THOMAS M T．Wave-induced motions of an air cushion structure in shallow water［J］．Ocean engineering，2006，33（8／9）:1143-1160．

［14］LE Conghuan，DING Hongyan，ZHANG Puyang．Air-floating towing behaviors of multi-bucket foundation platform［J］．China ocean engineering，2013，27（5）:645-658．

Research on the heave motion characteristics of a towed large air floating caisson

DING Hongyan1，2，3，ZHU Yan3，ZHANG Puyang1，2，3，LE Conghuan1，HAN Yanqing2
（1．State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2．Key Laboratory of Coast Civil Structure Safety，Tianjin University，Ministry of Education，Tianjin 300072，China；3．School of Civil Engineering，Tianjin University，Tianjin 300072，China）

To prevent contact between the seabed and a large air floating caisson in shallow waters due to large heave when towing，the heave motion characteristics of the caisson are studied in this paper．The analytic software MOSES was used to obtain the vertical displacement of the caisson due to irregular waves．Then，fast Fourier transform of this displacement and the Welch algorithm were used to acquire the natural heave period of the caisson．To obtain the range of the cycle corresponding to the maximum displacement amplitude point of the heave motion，regular waves of different periods were used to simulate the towing process of the caisson．Moreover，the calculation process of the theoretical natural heave period was analyzed，and the influence on the heave motion of the caisson with different drafts was studied．It is proven that the natural heave period can be reasonably obtained using MOSES and a power spectrum estimation method．The natural heave period can be used in the hydrodynamic calculation and as the standard value when selecting the additional mass factor．With an increase in the draft or a decrease in the cabin pressure，the natural heave period shows an increasing trend．

air floating caisson；natural heave period；added mass factor；heave；towing；wave

10．11990／jheu．201510015

http：／／www．cnki．net／kcms／detail／23．1390．u．20160928．0936．026．html

P752

A

1006-7043（2016）12-1665-06

丁红岩，朱岩，张浦阳，等．大型气浮沉箱拖航过程中的垂荡运动特性分析［J］．哈尔滨工程大学学报，2016，37（12）:1665-1670．

2015-10-10．

2016-09-28．

国家自然科学基金项目（51309179）；国家自然科学基金一般项目（14JCQNJC07000）．

丁红岩（1963-），男，教授，博士生导师；

张浦阳（1978-），男，副教授．

张浦阳，E-mail:zpy_td＠163．com．

DING Hongyan，ZHU Yan，ZHANG Puyang，et al．Research on the heave motion characteristics of a towed large air floating caisson［J］．Journal of Harbin Engineering University，2016，37（12）:1665-1670．