燃气射流引起的火箭发射系统振动特性分析

李军，于思淼，刘晴，胡亚，周为浩

（南京理工大学机械工程学院，南京210094）

燃气射流引起的火箭发射系统振动特性分析

李军，于思淼，刘晴，胡亚，周为浩

（南京理工大学机械工程学院，南京210094）

以火箭发射系统为研究对象，对其56°射角工况下发射过程中的振动特性进行分析。创新点在于确定发射过程中动态载荷的加载方法，即首先根据发射系统有限元分析结果确定迎气面上试验测量点的具体位置，然后测得燃气射流冲击压强随时间变化的数值，并对试验测得数据进行处理，最后推导冲击压力对于径向距离的直线公式。所采用的冲击压强分析方法为研究其他武器系统受燃气射流冲击的影响提供了重要的指导意义。

火箭发射系统，燃气射流，冲击压强，振动特性，有限元分析

0 引言

在火箭弹发射过程中，火箭发动机的燃气射流对发射装置有较大的冲击力，能引起发射装置弹性系统的振动，还可能增加连续射弹的起始扰动，因此，研究火箭炮的振动特性对提高其射击精度具有重要意义。但是，燃气射流属于湍流射流，具有瞬息变化和杂乱无章的性质，其加载方法无法逼近实际变化规律，因而导致由冲击力引起的振动影响难以确定。但燃气射流杂乱无章的特性实际上是随机性的表现，可应用统计概念给出各种气动参量，例如压力的平均值，从而有可能对燃气射流的运动规律进行数学上的描述。本文中采用冲击压力对面积的积分形式来表征冲击力的大小，因此，载荷的确定最终归结于冲击压强的变化规律。根据文献［1］的火箭燃气射流对多管发射装置的冲击流场机理，可以得出燃气射流在迎气面上按同心圆分布，即同一径向距离位置上的冲击压力变化规律近似相等。每一时刻的压强与压强极值之比为压强幅值，由试验可以测得冲击压强随时间的变化规律，推导出压强幅值。这种新型的冲击力加载方法为研究燃气射流对发射系统振动影响提供新方法。

文献［2］应用多重动态子结构法分析了某型多管火箭炮的振动特性；文献［3］建立了相应的多体火炮系统振动的传递方程和传递矩阵，求得有关多体火炮系统振动的频率方程和振型函数的解析式；文献［4］基于高斯最小拘束原理建立了火炮系统的多体动力学模型，根据推导的封闭式的动力学方程解析式。而本文对火箭发射系统全柔性体模型进行振动分析，进一步提高了仿真计算精度。

在确定合理的动态载荷加载方法后，在56°射角工况下，对发射系统应用新的载荷加载方式进行有限元分析［5］，得到发射系统动力学模型的振动特性参数。

1 数学模型建立

根据工程实际的几何尺寸建立发射系统的几何模型，整体模型示意图如图1所示，底架上部发射装置构建通过底圈与底架连接，运载体通过后左右支架和前支架与底架连接。另外，为进行系统的振动分析，在动力学模型中建立全局坐标系OXYZ，坐标原点O位于后部左右支架连线的中点上，X轴与俯仰角、方向角和回转角均为零度时的定向器轴线平行，指向前方；Y轴在后部左右支架连线上，由后右支架指向后左支架；Z轴与X、Y轴组成笛卡尔坐标系，符合右手定则，竖直向上。

图1 发射系统模型示意图

本文主要关注发射过程中燃气射流作用在火箭炮引起面上引起整个发射系统产生的振动影响，定向管的迎气面几何模型和网格划分如图2所示。

图2 迎气面有限元模型

2 压强的试验测量与处理

2.1 试验测点布置

对于多管火箭发射装置，当第n发火箭弹飞离定向器时，其喷出的燃气冲击于发射装置迎气面产生的压力分布为p（r，x），冲击力见式（1）。

式（1）中，An表示发射第n发火箭弹时发射装置迎气面承受压力作用的有效面积，r为迎气面上测量点距发射管中心的径向距离，x为火箭发动机喷口截面距迎气面的轴向距离。

由式（1）可知影响燃气射流冲击压强变化的主要因素是轴向距离x和径向距离r，因此，布置了8个测点，每一个测点距发射中心的径向距离都不相同，可从8组数据中得到冲击压强的变化规律。本次实验共发射高温、常温、低温3种弹，本文只对常温弹（温度大约为17℃）发射时冲击压强进行研究。测点具体布置如图3所示。

图3 测点位置

2.2 压强随径向距离的变化规律

根据试验测试所得数据，可以得到冲击压强实际变化规律曲线，如图4所示。根据冲击压强的变化规律，用压强随径向距离的公式划分冲击压强在迎气面上的分布；通过压力幅值选项（Amplitude）来描述载荷参数随时间的变化；燃气射流冲击压强值等于两者相乘［6］。

图4 冲击压强变化曲线

因为计算模型复杂，需要配置极高的计算机，为了提高工作效率，需选定最佳的冲击压强作用时间段。要求在最佳时间段内，所有测量通道的冲击压强都经历从增长到衰减的过程，或至少有增长到最值的过程。从压力传感器开始有信号算作测试的零点，由测得数据可见其零点为0.447 s，最佳作用时间段为0.55 s～0.65 s，然后对其进行归零处理。根据压力随时间的变化规律，利用列表法可以计算得到冲击压强幅值（A）在100 ms内的变化规律如表1所示。

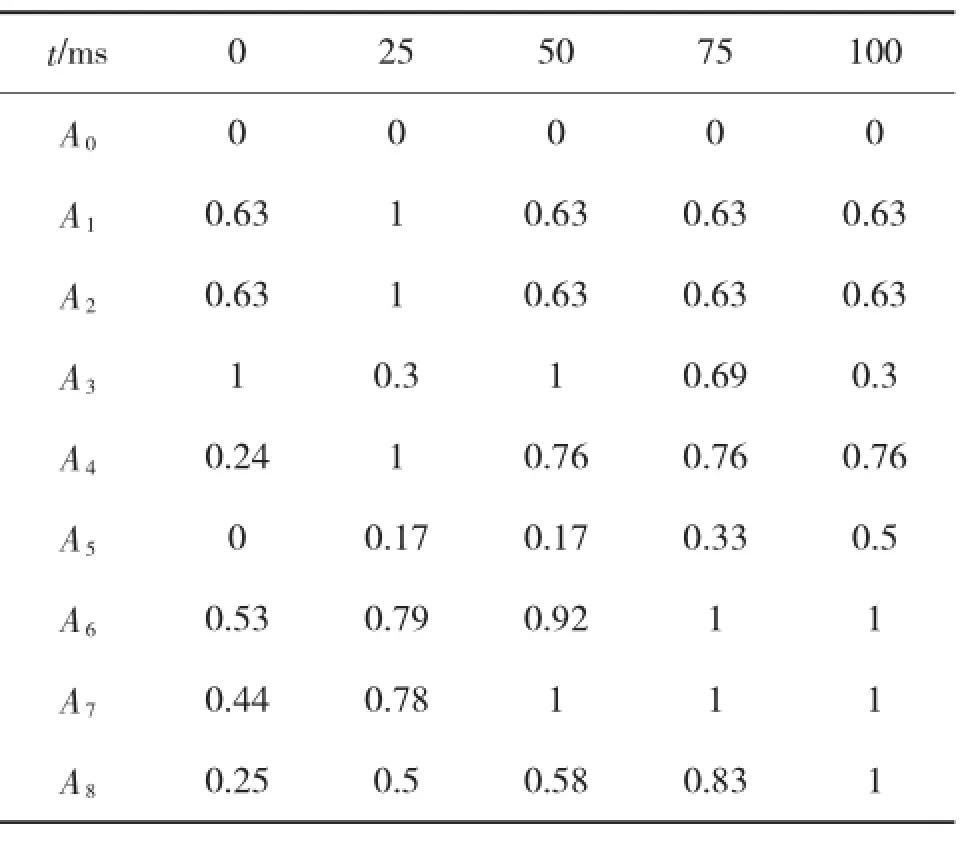
表1 压强幅值变化规律

2.3 压强随轴向距离的变化规律

8个径向距离r1～r8对应的冲击压力p1～p8随时间的变化规律见图4，在测量末尾时间段有些压力值不归于零，这是由于测量误差引起的，在此关于测量问题不多作介绍。由图5可知到发射管中心的径向距离为300 mm对应的压强p1值在增长时间段和衰减时间段每一时刻都是最大的；p3和p5的压强值变化时间段都近似相等，除个别增长时间段的冲击压强值外，两者的曲线近似重合；到发射管中心的径向距离为400 mm的位置对应的p2和到发射管中心的径向距离为600 mm的位置对应的p6衰减阶段保持一致，并且达到峰值时间相同，但是增长阶段有一定的差异；p4在整个测量时间内只有负压的变化，只有p7压强峰值最大为0.1 MPa，p8压强峰值最大为0.05 MPa，也就是说径向距离大于900 mm点的冲击压强值变化很小，在迎气面位置上大于这个范围的冲击压强可以近似不考虑。对最大值p1进行具体分析，在0 ms～150 ms时间段内，以近似线性函数增长，达到最大值0.48 MPa，因此，可以得到压强随时间的直线方程，进而得到压强随时间的幅值A，见表1；在100 ms～200 ms时间段内围绕最大值上下波动，从200 ms后压强值开始衰减，在450 ms后保持0.08 MPa不变。

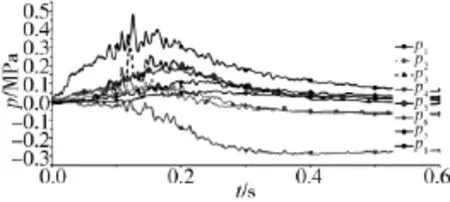
图5 压强随时间的变化趋势

3 动力学模型振动特性分析

根据前文中压强随径向距离的直线方程和压强幅值的表格，在发射系统迎气面上加载压力载荷，如图6所示。在储运发射箱上设定了4个监测点，左发射箱左上角第1根定向管的迎气面中心设为监测点1，其管尾部中心点设置为第3个监测点；右发射箱左上角第1根定向管的迎气面中心设为监测点2，其管尾部中心点设置为第4个监测点。

图6 燃气射流冲击压强的加载

3.1 储运发射箱的动态响应

3.1.1 储运发射箱的加速度变化规律

在常温弹的发射过程中，4个监测点在全局坐标系下进行分析，包括X、Y、Z 3个方向的加速度随时间的规律曲线。全局坐标系中X方向的加速度见图7，监测点1和监测点2加速度变化幅值范围比较大，监测点1最大值在30 m/s2左右，监测点2最大值在50 m/s2左右，这说明定向管迎气面上的作用力很大。监测点3和监测点4在X方向的加速度在-5 m/s2和5 m/s2之间均匀波动，且周期性变化，由此可见由定向器管口传递到定向器管尾部的作用力相对较小。

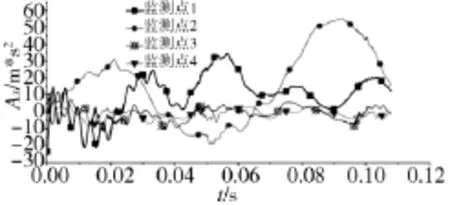
图7 X方向加速度变化

图8 Y方向加速度变化

全局坐标系中Y方向的加速度见图8，4个监测点的加速度都为周期性变化，变化的幅值和周期有一定的差异。监测点1以25 ms为一个周期，最大值在20 m/s2左右，从40 ms以后最大值稳定在10 m/s2左右，最小值在-15 m/s2，周期性变化。监测点2、监测点3和监测点4Y轴的加速度变化规律比较相似，一般都是在-10 m/s2和10 m/s2之间均匀波动，且周期性变化，只有少数的时间点可以达到15 m/s2。除了测点一之外的其他3个测点的Y向加速度都比较小，由此可见由燃气射流冲击引起的作用力在定向器管Y方向传递的相对较小。

全局坐标系中Z方向的加速度见图9，4个测点的加速度变化曲线相似，只是达到最大值的时间点有差异。监测点1和监测点3的加速度在0 ms～40 ms之间抖动频繁，监测点1加速度由30 m/s2减小到-30 m/s2，监测点3加速度由20 m/s2减小到-10 m/s2，在0 ms～40 ms之间时分别增加到10 m/s2和15 m/s2。监测点2和监测点4的加速度在0 ms～20ms之间分别减小到-30 m/s2和-10 m/s2，到80ms时分别增加到25 m/s2和15 m/s2，然后在后续时间内周期性变化。可以得出结论，储运发射箱在Z方向的加速度变化剧烈，且加速度波动较大。

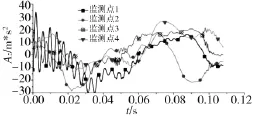
图9 Z方向加速度变化

3.1.2 储运发射箱的位移变化规律

定向器在全局坐标系下X方向的位移变化曲线见图10，监测点1和监测点2规律曲线走势相似，在0 ms～140 ms时间段内从零位移向X轴负向移动，最大位移量达到60 mm左右，这说明在燃气射流冲击下定向管关口在X方向发生了较大的位移量。监测点3和监测点4的位移曲线近似重合，位移量最大值为5 mm，由此可见定向管尾部在X方向发生的位移量可以忽略不计。可见燃气射流冲击引起的迎气面X方向振动位移最大达到60 mm，尾部产生的X方向振动位移可以忽略。

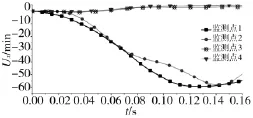
图10 X方向位移变化

在全局坐标系下定向器Y方向的位移变化曲线见图10，监测点1和监测点2的位移规律曲线走势相似，在仿真分析的整个时间段内从零位移向Y轴正向移动，最大位移量达到30 mm左右，这说明在燃气射流冲击下定向管关口在Y方向发生了较大的位移量。监测点3和监测点4的位移曲线近似重合，位移量最大值为-5 mm，由此可见定向管尾部在Y方向发生的位移量相对管口位移量较小。可得出结论，燃气射流冲击引起的迎气面Y方向振动位移量大约为X方向位移量的一半，尾部产生的Y方向振动位移与X方向振动位移相同。

图11 Y方向位移变化

在全局坐标系下定向器Z方向的位移变化曲线见图12，监测点1和监测点2的位移规律曲线走势相似，在仿真分析的整个时间段内从零位移向Z轴正向移动，最大位移量达到15 mm左右；监测点3和监测点4的位移曲线近似重合，位移量最大值分别为-35 mm和-25 mm，定向管尾部在Z方向发生的位移量可相对管口位移量而言比较大。综上可得，燃气射流冲击引起的迎气面Z方向振动位移量大约为X方向位移量的1/3，尾部产生的Z方向振动位移超过其他两个方向振动位移，这说明储运发射箱的56°射角在发射过程中受燃气射流冲击的影响而增大。

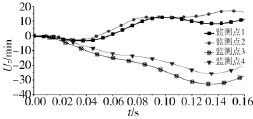
图12 Z方向位移变化图

赋予发射系统定向管综合位移20倍的放大系数，如图13所示。

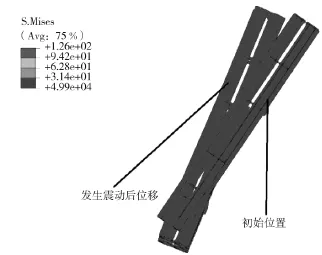
图13 Z方向位移变化

3.2 发射装置的刚强度分析

燃气射流冲击力对夹板产生的最大应力值出现在t=130 s第1道夹板上的左下定向管与夹板的结合处，最大应力达到50 MPa，如图14所示。

图14 第1道夹板的应力

4 结论

本文主要研究了多管火箭发射装置在前发火箭弹飞离定向器时发射装置受到燃气射流影响而承受的燃气动力干扰。根据发射时迎气面上冲击压强随时间的变化规律，应用新的载荷加载方式对发射系统进行振动特性分析，可以得出如下结论：

（1）由于火箭弹发射时产生离轴姿态角造成了压强值在起始阶段先减小到负值。取得峰值为0.48MPa，在迎气面上大于900 mm的位置上的冲击压强可以忽略。

（2）X方向的加速度与Y方向的加速度变化规律一致，近似为周期性变化；Z方向与X、Y方向相比，加速度值比较小，说明储运发射箱在Z方向所受冲击力最小。

（3）储运发射箱炮口产生的X负方向位移达到60 mm，运发射箱尾部的X正方向位移只有5 mm，可以忽略不计；运发射箱炮口产生的Y正方向位移最大到30 mm，储运发射箱尾部产生Y负方向位移5 mm；运发射箱炮口产生的Z正方向位移最大到15 mm，运发射箱尾部产生Z负方向位移30 mm。

（4）对发射系统进行动力学仿真分析，得出储运发射箱第1道夹板上左下定向管与夹板的结合处出现了应力最大值，大约为50 MPa。

［1］张福祥.火箭燃气射流动力学［M］.哈尔滨：哈尔滨工程大学出版社，2004.

［2］王彦平，申正宾.用动态子结构法分析火箭炮的振动特性［J］.太原机械学院学报，1989，11（02）：11-14.

［3］芮筱亭，邱风昌.多体火炮系统的固有振动特性──多体系统动力学的传递矩阵法［J］.兵工学报，1995，17（02）：25-29.

［4］史跃东，王德石.高斯最小拘束原理在火炮振动分析中的应用［J］.火炮发射与控制学报，2009，31（04）：91-94.

［5］张建海，韩迎春，曾艳艳，等.时频分析方法及其在火箭振动数据分析中的应用［J］.四川兵工学报，2015，36（11）：86-90.

［6］马晓峰.ABAQUS 6.11有限元分析从入门到精通［M］.北京：机械工业出版社，2013.

Analysis of Vibration of Rocket Launching System Caused by Gas Jet

LI Jun，YU Si-miao，LIU Qing，HU Ya，ZHOU Wei-hao
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China）

According to the results of finite element analysis，the experimental arrangement of measuring points is determined，and values of rocket gas jet impact pressure changing over time is measured；deal with the experimental data for later process，the linear formula of the impact pressure is derived.Determined the reasonable loading method，and at a 56 degree angle condition，the vibration characteristics of dynamic model further is studied.The method of impact pressure has reference significance to innovative design the analysis of other weapon systems.

rocket lunching system，gas jet，impact pressure，vibration characteristics，finite element analysis

TJ713

A

1002-0640（2016）12-0108-05

2015-10-25

2015-12-29

李军（1965-），男，河南平顶山人，教授。研究方向：火箭导弹发射系统结构设计。