基于SD的信息化防御作战中兰彻斯特方程

卞立新，罗兴柏，刘国庆，甄建伟

（军械工程学院，石家庄050003）

基于SD的信息化防御作战中兰彻斯特方程

卞立新，罗兴柏，刘国庆，甄建伟

（军械工程学院，石家庄050003）

在对信息化条件下的防御作战进程分析的基础上，增加信息因素和兵力补充速度对经典的兰彻斯特方程进行改进。通过引入系统动力学方法，构建了信息化条件下的防御作战进程的系统动力学模型，利用系统动力学方法来对改进的兰彻斯特方程进行求解。仿真结果证明了系统动力学在解决复杂兰彻斯特方程中的优越性。

系统动力学，兰彻斯特方程，信息化作战

0 引言

随着科学技术的不断发展，以及信息化技术在现代战争中的广泛使用，现代战争形势发生了巨大变化，信息成了决定战争胜败的关键因素。兰彻斯特方程在作战模拟中有广泛的应用，然而经典的兰彻斯特方程以不能满足现在的作战形势，针对信息化条件下的作战形势，文献［1-3］在经典的兰彻斯特方程基础上进行改进，建立了符合信息化条件下的战斗模型，然而改进的兰彻斯特方程具有多维、高阶和非线性的特点，利用常规的数学手段很难求解方程，利用降阶、线性等近似手段虽然能使求解变得容易，但是得到的解很不可靠［4］。

系统动力学（System Dynamics，SD）由美国麻省理工学院福瑞斯特（Yay W.Forrester）教授于1956年创立。是一门分析研究信息反馈系统的学科［5］。SD通过定性与定量相结合的方法来解决系统问题，利用作战进程中各变量之间的因果关系来解决建模难题。SD可以将复杂作战背景下的高阶的兰彻斯特方程通过因果关系和流图转化为SD模型，进而对兰彻斯特方程进行求解。

1 经典兰彻斯特方程

兰彻斯特方程是英国的工程师兰彻斯特（Lanchester）通过对飞机在战争中的使用问题进行分析而提出来的，包括兰彻斯特线性律和兰彻斯特平方律［6］。兰彻斯特线性律是兰彻斯特根据远距离战斗而得出的。其假定条件有两个，第一是战斗双方兵力互相隐蔽；第二是每一方火力集中在对方战斗成员的集结区域，不对个别目标实施瞄准，火力为面火力。兰彻斯特平方律是建立在近代战斗模型基础上。其基本假定有3条，第一是双方兵力互相暴露；第二是每一方都可以运用他们的全部兵力并集中火力射击对方的兵力；第三是双方战术指挥通信处于最佳状态［7］。

1.1 兰彻斯特方程线性律

兰彻斯特方程线性律数学模型如下：

式中：R为红方兵力数量，B为蓝方的兵力数量，β为蓝方被红方的消耗速率，即蓝军在单位时间内损失的兵力，α为红方被蓝方的消耗速率，即红方在单位时间内损失的兵力，R，B，β，α均大于0。

1.2 兰彻斯特方程平方律

兰彻斯特方程平方律数学模型如下：

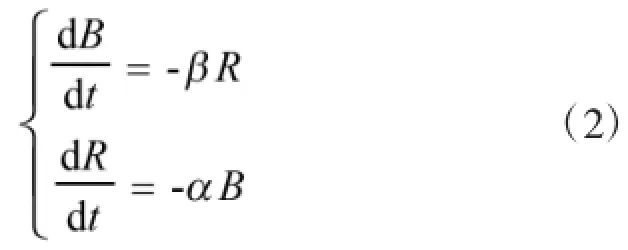
式中：R为红方兵力数量，B为蓝方的兵力数量，β为蓝方兵力在单位时间内被红方单个兵力毁伤的数量。α为红方兵力在单位时间内被蓝方单个兵力毁伤的数量。

2 信息化战争中的兰彻斯特方程

2.1 信息化条件下的战斗模型

经典兰彻斯特方程中的线性律和平方律需要在假定相互隐蔽和相互暴露的条件下使用，而信息化条件下的战争中这种假定条件很难实现，因此，单独使用经典兰彻斯特方程无法对信息化条件下的作战进程进行准确描述。文献［3］在经典兰彻斯特方程的基础上给出了信息化条件下的战斗模型：

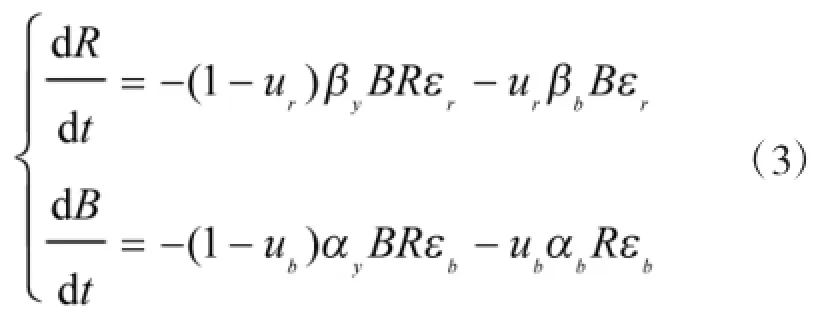
式中，βb、αb分别表示红方、蓝方对对方暴露敌方士兵的杀伤率，称为暴露毁伤系数，βy、αy分别表示红方、蓝方对对方隐蔽敌方士兵的杀伤率，称为隐蔽毁伤系数，εr、εb分别为红方、蓝方战场使用信息的能力［3］。ur、ub为战场暴露系数由下式得出。

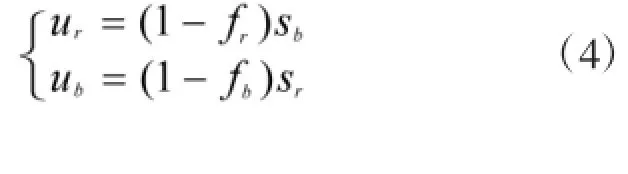
式中，fr、fb为红、蓝方的伪装能力系数，sb、sr为红、蓝方的侦察能力。

式（3）考虑了信息在战争中的重要作用，还需要考虑在信息化条件下防御作战中防御的一方处的兵力补充。对防御方红方增加兵力补充速度n，得到修改后的模型如下：

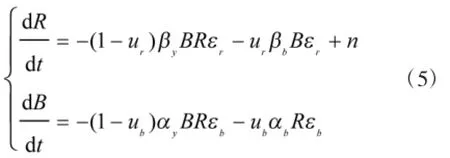
2.2 对兰彻斯特模型求解

常规的方法对于方程（5）的求解十分困难，本文借助SD方法对模型进行分析求解。根据红方战斗力和蓝方战斗力之间的相互作用关系，补充影响战争进程的其他因素，对该作战的模型利用SD方法进行描述，得到作战系统因果关系图，如图1所示。

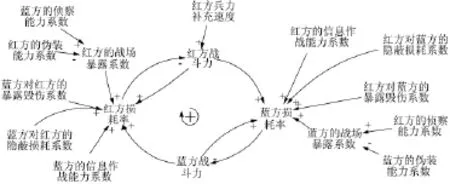
图1 红蓝双方作战的因果关系图

从图1可知该作战模型是以红方战斗力---＞+蓝方损耗率---＞-蓝方战斗力---＞+红方损耗率---＞-红方战斗力这一闭合回路为基础，在此基础上不断添加影响战争的各种因素从而完善作战模型。

在对红蓝双方作战的因果关系图分析的基础之上建立红蓝双方的作战流图，如图2所示。

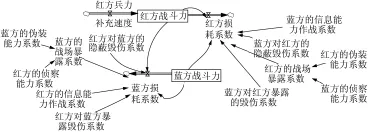
图2 红蓝双方的作战系统流图

3 仿真实验和结果分析

基于上述提出的信息化作战中的兰彻斯特方程，通过SD仿真软件VensimPLE运行该模型，分以下3种仿真假设情况进行仿真计算。

3.1 仿真假设1

红蓝双方的信息化水平和兵力相当，蓝方的毁伤系数大于红方，但红方有不断的兵力支援。故假设红方初始兵力R（0）=5 000，蓝方初始兵力B（0）= 5 000，βb=0.1，αb=0.2，βy=0.000 01，αy=0.000 02，εr=εb= 4，fr=fb=0.6，sr=sb=0.4，红方的兵力补充速度为400人/天。仿真结果如图3所示。

图3 n=400时红蓝双方的战斗力量变化图

从图3结果可以看出：红方和蓝方在初始兵力、侦察、伪装以及信息作战能力均相同时，由于蓝方隐蔽毁伤系数和暴露毁伤系数比红方大，使得在作战初期红方处于劣势，作战兵力迅速减少；但红方不断有兵力补给，使得红方最终处于战争优势，并且取得战争的胜利彻底消灭蓝方。这也与实际的作战情况相符合，说明了仿真结果的准确性。

3.2 仿真假设2

红蓝双方的毁伤系数和兵力相当，红方兵力处于劣势，并且没有兵力补充，分析不同暴露系数对战争结果的影响。故假设红方初始兵力R（0）=5 000，蓝方初始兵力B（0）=5000，βb=αb=0.1，βy=αy=0.00001，εr=εb=4，红蓝双方的伪装能力和侦察能力系数见表1所示。

表1 能力系数表

不同能力系数下的仿真结果如图4，图5所示。

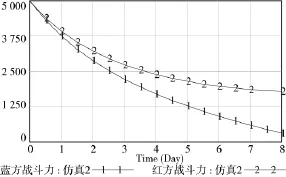
图4 序号1的仿真结果

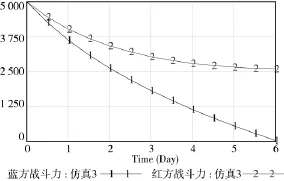
图5 序号2的仿真结果

从图4可知，在红方和蓝方的兵力和毁伤系数相等的情况下，由于红方的侦察能力和伪装能力高于蓝方，兵力毁伤上有较大差距，红方用大概8个单位时间就完全消灭了蓝方，取得战争的最终胜利；当红方大幅提高己方的侦察能力和伪装能力时，红方用大概6个单位时间就完全消灭了蓝方，并且损失更少的兵力。通过图4和图5可得出信息对于作战进程影响很大，在双方人数、毁伤系数相等的情况下，获取信息优势的一方能迅速击败敌方。利用SD方法仿真得到的结果与文献［3］所得结果基本相同，而利用SD对于方程的求解更加简单，省去了大量繁琐的计算，也证实了SD方法的优越性。

3.3 仿真假设3

红蓝双方的信息化水平和兵力相当，蓝方的毁伤系数大于红方，假设红方初始兵力R（0）=5 000，蓝方初始兵力B（0）=6000，βb=αb=0.1，βy=αy=0.00001，εr=εb=4，fr=0.4，fb=0.8，sb=0.6，sr=0.4，红方的兵力补充速度分别为n=300人/天和n=450人/天。仿真结果如图6，图7所示。

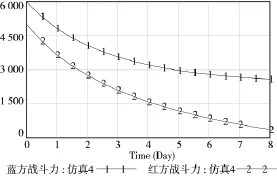
图6 n=300人/天的仿真结果

图7 n=450人/天的仿真结果

从图6和图7可知，当红蓝双方在毁伤系数相同的情况下，由于蓝方的兵力和信息化水平高于红方，即使红方在有兵力补充的情况下，依然很快被蓝方消灭。当红方大幅提高己方的兵力补充速度时，红方的优势开始显现，在第15个单位时间左右打败蓝方，取得战争胜利。

通过仿真结果可以看出信息对于战争的重要性，信息优势的提高可以大幅减少己方的兵力消耗，并且可以缩短作战时间。在兵力和信息都处于劣势的情况下，就需要己方部队的快速增援，才有可能取得战争的胜利。

4 结论

通过对信息化条件下的防御作战分析的基础上，利用SD方法构建了信息化条件下防御作战的系统因果关系图和系统流程图，仿真证明了信息对于战争的重要性，决定战争胜败的关键因素。在防御作战中，在兵力和信息都处于劣势的一方要及时补充兵力，才可能反败为胜。SD方法对实例的仿真计算表明，SD对于求解复杂的高阶改进的兰彻斯特方程具有建模简单、容易理解、数值计算方便、仿真结果准确等优点。

［1］周奕，周锦鹏，郝维平.基于兰彻斯特不同信息条件下的空战效能分析［J］.航天控制，2006，24（2）：54-57.

［2］吴俊，杨峰，梁彦，等.面向信息化战争的广义兰切斯特作战模型［J］.火力与指挥控制，2010，35（2）：50-53.

［3］占栋辉，陈刚，张宏军，等.现代化战争条件下的兰切斯特战斗模型［J］.计算机工程与应用，2013，49（15）：246-248.

［4］王可定.作战模拟理论与方法［M］.长沙：国防科技大学出版社，1999.

［5］王其藩.系统动力学［M］.上海：上海财经大学出版社，2009.

［6］美国陆军武器装备研制与采购司令部.陆军武器系统分析（下册）［M］.兵器工业部兵器系统工程研究所译.北京：兵器工业出版社，1986.

［7］郭齐胜，邵志刚，杨瑞平.装备效能评估概论［M］.北京：国防工业出版社，2005.

Studyon Information DefensiveBattleLanchester Equation Based on SD

BIAN Li-xin，LUO Xing-bai，LIU Guo-qing，ZHEN Jian-wei
（Ordnance Engineering College，Shijiazhuang 050003，China）

On the basis of analysis defensive combat processes under conditions of information，information factors and the forces speed to improve classical lanchester equation are added.Make up the defensive combat processes system dynamics model under conditions of information，according the method of system dynamics，the improved lanchester equation is solved by using system dynamics method.From the example，the advantage of computing complex lanchester equations with system dynamics can be found.

system dynamics，lanchester equations，information warfare

E91

A

1002-0640（2016）12-0105-03

2015-11-01

2015-12-23

卞立新（1991-），男，辽宁本溪人，硕士研究生。研究方向：弹药系统设计与试验评估。