相控阵雷达维修方案优选方法研究*

王永攀，杨江平，张可心，张伟

（空军预警学院，武汉430019）

相控阵雷达维修方案优选方法研究*

王永攀，杨江平，张可心，张伟

（空军预警学院，武汉430019）

针对相控阵雷达维修方案的选择问题，确定了维修方案的决策属性，并提出一种基于改进TOPSIS法的相控阵雷达维修方案优选方法。该方法通过引入Vague集来处理维修方案选择中存在的模糊信息，并采用博弈论综合赋权法来确定决策属性的综合权重。通过计算各备选方案与正、负理想方案的灰色关联度，得到了维修方案的灰色关联相对贴近度，进而实现对维修方案的排序和选择。最后，通过算例应用与分析，对提出的方法进行了验证。

维修方案，相控阵雷达，TOPSIS法，Vague集，灰色关联度，博弈论

0 引言

相控阵雷达在国家防空、反导等军事领域中有着广泛的应用，其地位和作用毋庸置疑［1-2］。对其维修方案进行科学、合理的选择是相控阵雷达效能得到有效发挥的根本保障。因此，围绕相控阵雷达维修方案的优选问题展开研究，意义重大。当前，在方案优选问题研究领域，可选择的方法较多，如层次分析法［3］、灰色关联分析法［4］、TOPSIS法［5］等，其中，由于TOPSIS法及其拓展方法在解决多属性决策问题方面良好的表现得到了广泛的应用［6-7］。为此，本文研究了一种基于改进TOPSIS法的相控阵雷达维修方案优选方法。首先，确定了相控阵雷达维修方案选择的决策属性。接着，引入Vague集和灰色关联度对TOPSIS方法进行了改进，并给出了具体的维修方案选择步骤。最后，通过算例应用与分析对提出的方法进行了验证。

1 维修方案决策属性

维修方案的优劣直接关系到相控阵雷达任务的有效完成。为了科学、合理地选择相控阵雷达维修方案，综合考虑各方面因素，确定了4个方面的决策属性用于选择维修方案，即维修质量、维修费用、维修进度和维修风险。下面进行具体介绍。

1.1 维修质量D1

维修质量是指相控阵雷达经过维护和修理后恢复到规定技术状态的程度，是表征维修方案优劣的重要标准。在一定的维修方案条件下，维修质量主要通过相控阵雷达的维修过程控制来保证，并且通过维修质量评价的结果来衡量。

1.2 维修费用D2

维修费用是指在一定的维修方案下对装备进行维修而产生的全部费用，包括人员费用、备件费用等。不同的维修方案，产生的维修费用不同。如果没有维修费用的约束，就会产生高额维修费用，从而产生巨大的财政负担。因此，在选择维修方案时，维修费用应是一个必不可少的决策属性。

1.3 维修进度D3

维修进度是指在规定维修时间内完成维修任务的程度，主要通过从雷达停机维修到重新开机运行之间的时间来衡量。维修进度与相控阵雷达能否顺利工作息息相关，如果缺少维修进度这一约束条件，就容易造成相控阵雷达维修工作的延迟，从而影响相控阵雷达执行作战任务。因此，维修进度也是维修方案选择必须重点考虑的决策属性。

1.4 维修风险D4

由于相控阵雷达结构复杂、系统较多，涉及专业、技术领域范围广，致使维修过程中不确定性因素较多，使得维修风险问题变得突出，因此，在选择维修方案时需要重点考虑。为保证维修方案顺利的实施，必须对维修风险进行评估。维修风险主要存在于技术、费用、进度等方面，通常用维修方案的失败率来表示，可以通过德尔菲法对维修风险等级进行确定。

2 维修方案优选模型

2.1 Vague集

Vague集［8-9］最初是在20世纪90年代由学者Gau和Buehrer等在扩展Fuzzy集的基础上提出来的。在一个点空间U中，元素x的Vague集通常用真、假隶属度函数来表示。其中，真隶属度函数tA（x）表示从支持x的证据导出的x的肯定隶属度的下界；假隶属度函数fA（x）表示从反对x的证据导出的x的否定隶属度下界。tA（x）和fA（x）将区间［0，1］中的一个实数映射到U中的每一个点，即

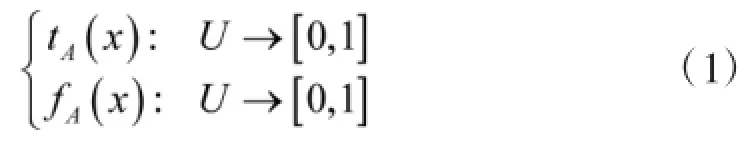
式中：0≤tA（x）+fA（x）≤1。在论域U中，区间A（x）=［tA（x），1-fA（x）］称为元素x在A中的Vague值。其中，πA（x）=1-tA（x）-fA（x）表示元素x对A的不确度，πA（x）满足条件0≤πA（x）≤1。论域U上两个Vague值A、B之间的距离d（A，B）可表示为

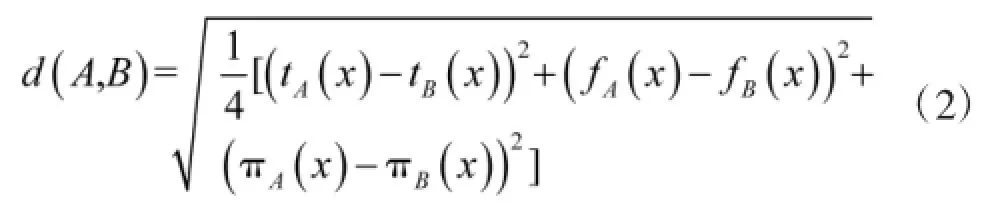
利用Vague集处理多属性问题的关键是进行属性值与Vague集的转化。对于定量属性指标中的效益型指标，其真假隶属度为

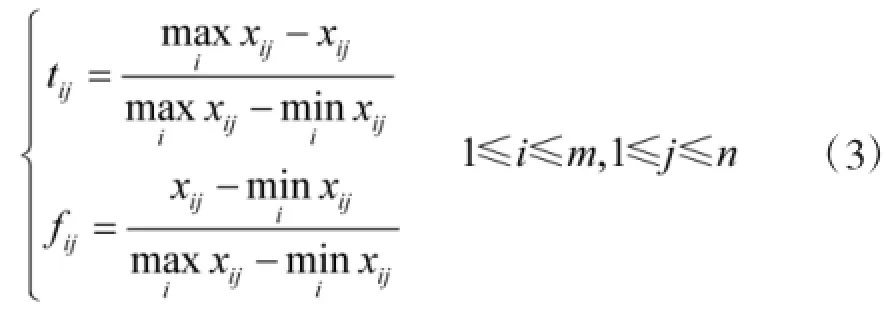
对于定量属性指标中的成本型指标，其真假隶属度为

对于定性属性指标，主要用属性等级区间划分来表示Vague值，如表1给出了一个具有5个属性等级的Vague值转化表。

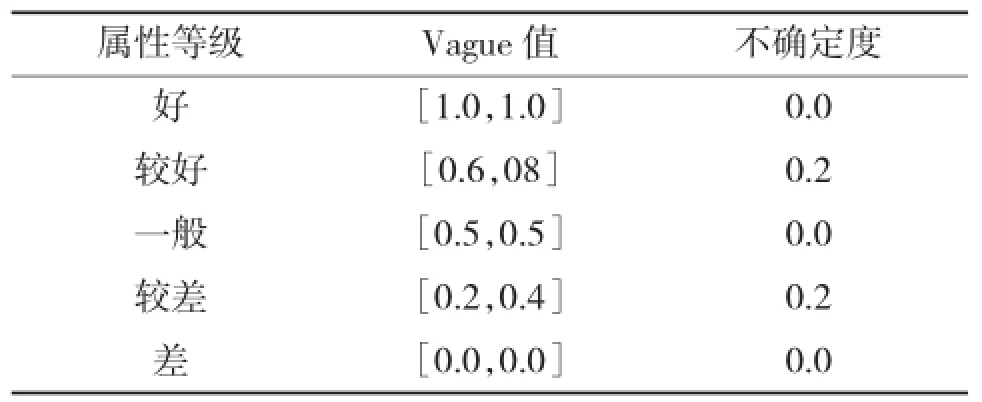
表1 Vague值表示的5级语言变量

为了更加详细地描述，可以将增加语言变量的等级数。值得注意的是，为了保证中间值近似接近0.5，通常设定语言变量的等级为奇数，从而形成两端的对称分布，更加方便描述。

2.2 基于改进TOPSIS法的维修方案优选模型

TOPSIS方法是逼近理想方案的排序方法，通过求解各备选方案与正、负理想方案的距离，进行排序后确定方案的优先级，最终筛选出最优方案。为了更好地对维修方案进行筛选，本文构建了基于改进TOPSIS法的维修方案优选模型。该模型通过引入Vague集来处理决策属性的不确定信息；通过博弈论综合赋权方法求得决策属性综合权重，使决策属性的权重更加合理；借鉴TOPSIS法细想，通过引入灰色关联度，最终确定任务条件下最优化的维修方案。下面进行具体介绍。

2.2.1 构造Vague集多属性决策矩阵

设有m个备选维修方案组成方案集P={P1，…，Pm}，n个决策属性组成决策属性集D={D1，…，Dn}，方案Pi对决策属性Dj的决策值为dij（i=1，2，…，m；j=1，2，…，n）。其中，dij既可以是数值也可以是语言值，根据Vague集生成方法，将决策值dij转换称Vague值［tij（dij），1-fij（dij）］，生成Vague矩阵A为

2.2.2 确定决策属性权重

赋权公式法［10］根据属性指标的数目及其在整个决策过程中的重要性排队等级确定决策属性的权重，客观性较强。排队等级是对属性指标按其重要程度进行的顺序排列，不同指标同等重要也可处于同一等级。式（6）给出了赋权公式法的计算公式，其中w1=1。式中：n为属性指标的数目，i为排队等级。

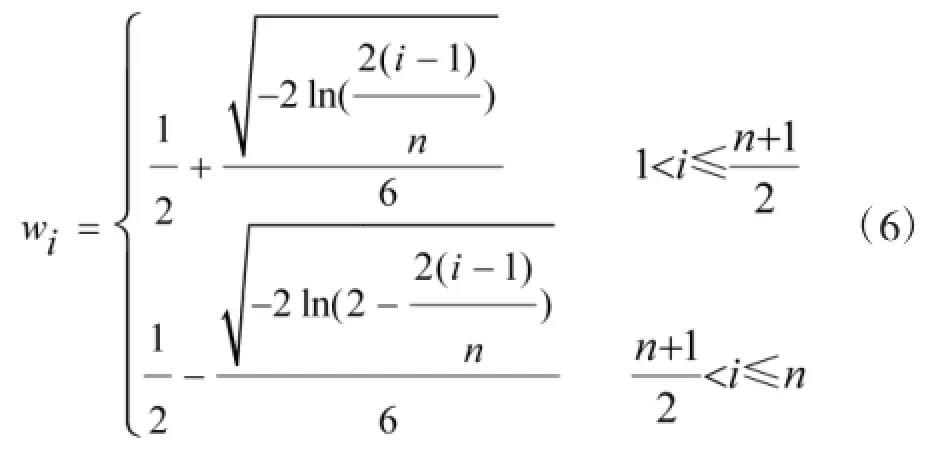
将wi作归一化处理即可得到客观权重woi。最终得到各属性的客观权重为W1={wo1，wo2，…，won}。

相对比较法［11］通过对任意两个属性指标的重要关系进行专家评定，组成评分矩阵，经过运算处理后得到各属性指标的权重。该方法主要依靠专家的经验知识对原始指标数据进行评定，能够较好地体现决策者和评估者的意图，主观性较强。为了使指标评定数据能够反映多数人的意志，本文利用德尔菲法对相对比较法进行了改进。具体如下。

首先，邀请决策属性相关领域内权威专家s人，采用三级比例标度对属性两两重要性进行评分。三级标度值qij及其含义为

设s个专家对属性i和j之间的重要性评定分数为qijk（k=1，2，…，s），则指标i和j的重要性平均评分为

进一步可求得各属性的主观权重wsi为

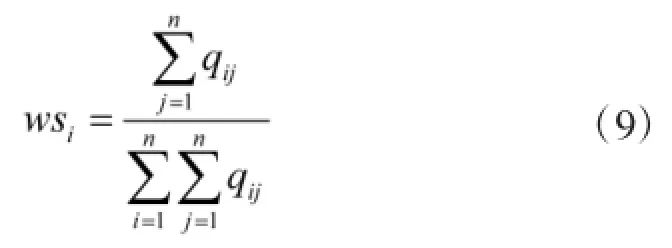
最终得到各属性的主观权重为W2={ws1，ws2，…，wsn}。

为了对得到的客观权重W1和主观权重W2进行有机的融合，使决策属性的权重更加科学、可靠，本文采用博弈论的方法对得到的属性权重进行处理。博弈论综合赋权法［12-13］的主要思想是通过在不同的权重之间寻找一致或妥协，使理想的综合权重与主、客观权重的偏差极小化，并尽可能地保留各主、客观权重值的信息。具体计算方法如下：

设主、客观权重的向量的线性组合为

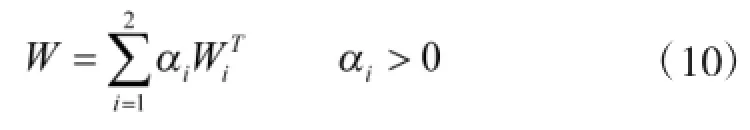
式中：αi为组合系数，且α1+α2=1。

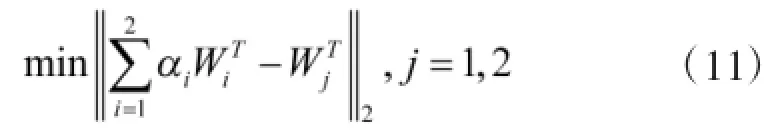
根据矩阵的微分性质，上述决策模型的最优化一阶导数条件为

其对应的线性方程为

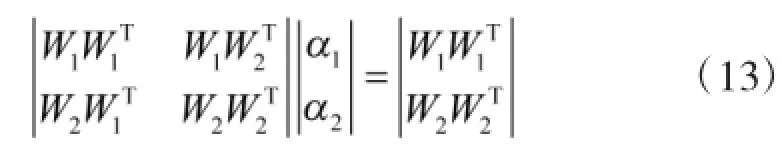
求解方程，将归一化后得到α1和α2，带入式（10）即可得到决策属性的综合权重W。

2.2.3 确定最优方案

首先，确定方案集P={P1，…，Pm}满足决策属性集D={D1，…，Dn}约束条件的正理想方案P+和负理想方案P-如下

式中：i=1，2，…，m。接着，计算各备选方案与正、负理想方案在所有属性上的灰色关联度。根据灰色关联分析理论［14-15］，方案Pi与P+和P-关于第j个指标的灰色关联度rPISij、rPISij可通过下式得到

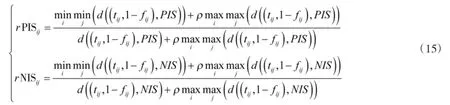
式中：PIS和NIS分别为正、负理想方案对应的Vague值。设wj为第j个决策属性的权重值，则方案Pi的正、负灰色关联度为

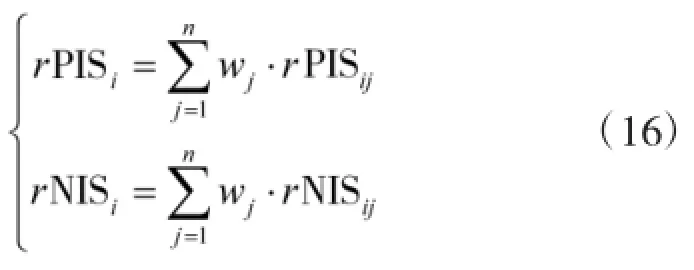
进一步可求得备选方案Pi的灰色关联相对贴近度μ（Pi）为

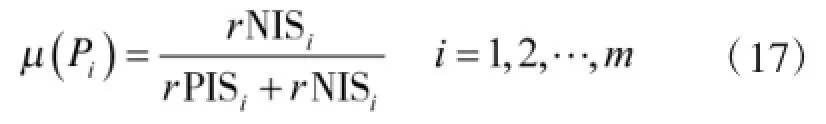
根据TOPSIS思想：μ（Pi）越大，表示方案Pi越接近正理想方案P+，反之，表示方案Pi越接近负理想方案P-。因此，根据μ（Pi）的大小对备选方案进行排序，最终可确定最优维修方案。

3 算例应用与分析

已知某型相控阵雷达有4个备选维修方案，试确定最优的维修方案以保证相控阵雷达效能的有效发挥。根据提供的维修方案，结合专家意见，给出表2所示的决策值数据。

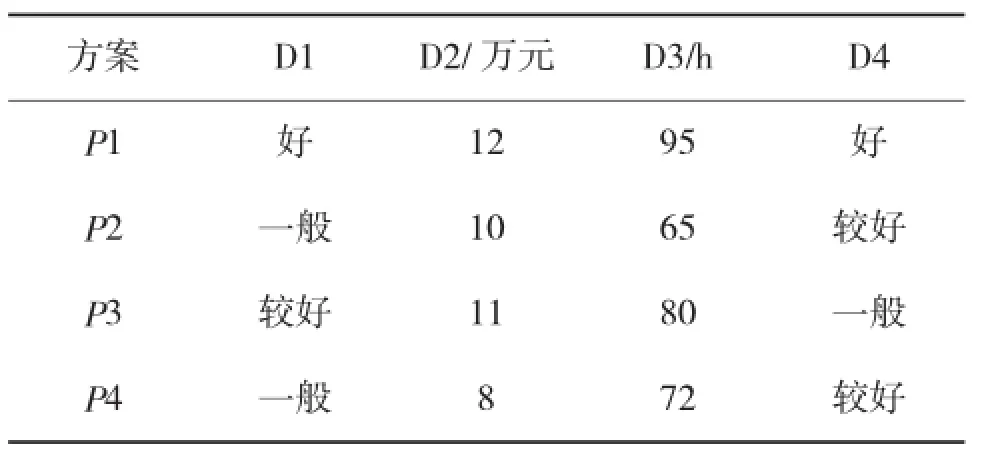
表2 方案对决策属性的决策值

根据2.1节Vague集理论知识对决策值进行Vague值转化。其中，对属性D2、D3按定量指标中的成本型指标进行转化，对定性指标D1、D4采用表1所示的5级语言变量进行转化。结合表2，可得到各方案对决策属性的Vague值，如表3所示。

进一步得到正理想方案的Vague值为PIS= {［1.00，1.00］，［1.00，1.00］，［1.00，1.00］，［1.00，1.00］}；负理想方案的Vague值为NIS={［0.50，0.50］，［0.00，0.00］，［0.00，0.00］，［0.50，0.50］}。

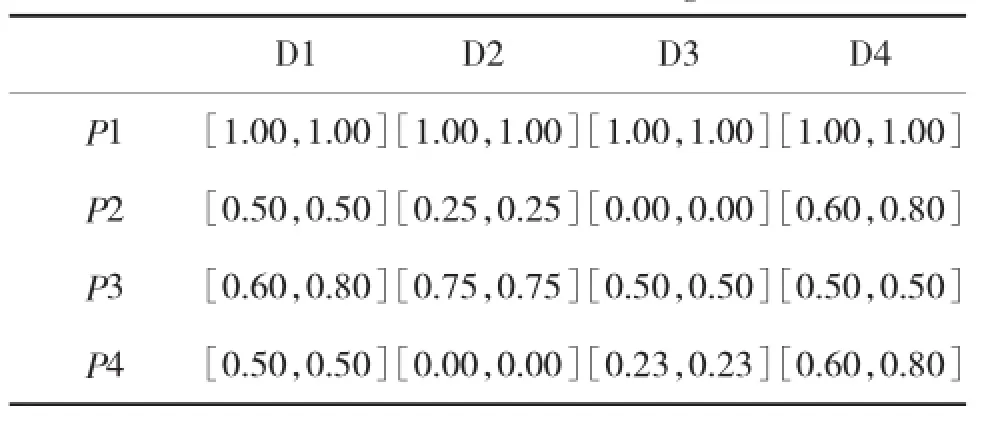
表3 各方案对决策属性的Vague值

通过博弈论综合赋权法得到决策属性的权重为W3={0.268 7，0.376 9，0.207 7，0.146 7}。

进一步求得各方案对正、负理想方案的灰色关联度分别见表4、表5所示。

表4 各方案对正理想方案的灰色关联度

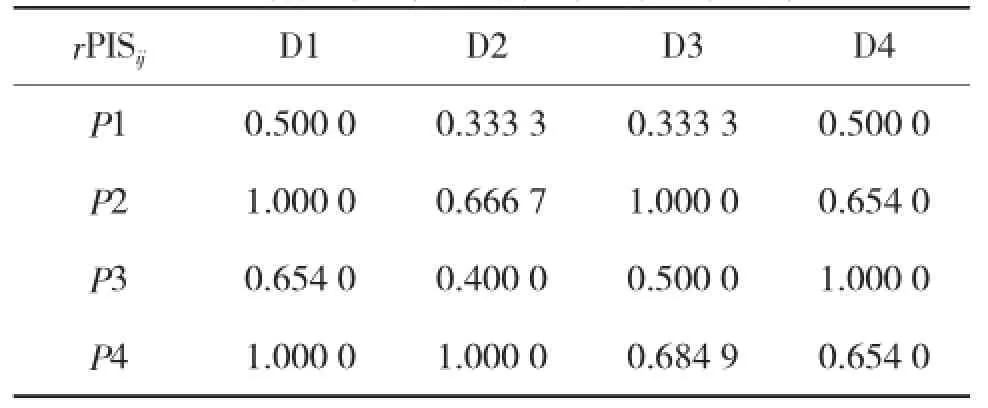
表5 各方案对负理想方案的灰色关联度

进而求得各方案的灰色关联度及贴近度，如表6所示。

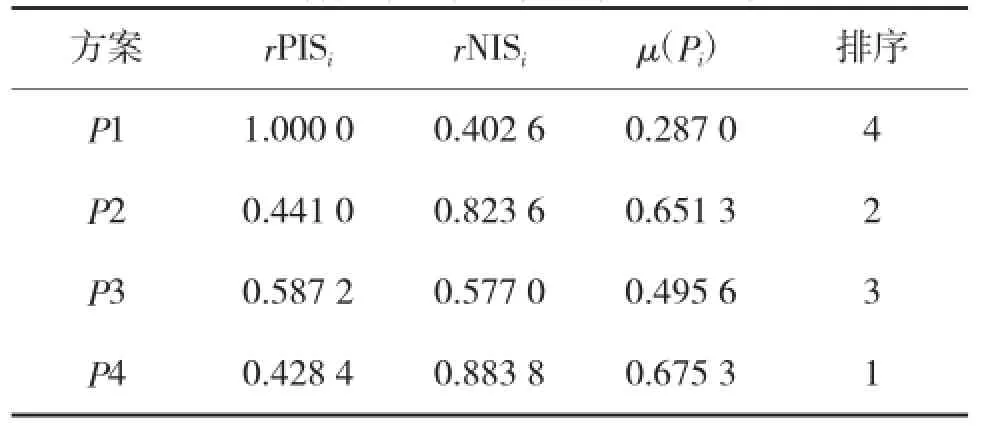
表6 各方案的灰色关联度及贴近度

从表6可以看出，各维修方案的排队顺序为P4＞P2＞P3＞P1，综合考虑，最优维修方案为P4。

分析各方案之间的分辨率：最大分辨率存在于方案P4与P1之间，分辨率为0.383 3；最小分辨率存在于方案P4与P2之间，分辨率为0.024 0。可见，该方法能够较好地区分各方案的优劣，为决策者定下决心提供有力的支撑。

4 结论

本文围绕相控阵雷达维修方案的优选问题展开了研究，提出一种基于改进TOPSIS法的维修方案优选方法，给出了方法的具体步骤，并进行了算例应用与分析。结果表明：提出的方法能够在一定程度上解决相控阵雷达维修方案的选择问题，具有一定的理论和现实意义。

［1］HERD J，DUFFY S，CARLSON D，et al.Low cost multifunction phased array radar concept［C］//Proc.of 2011 IEEE International Symposium on Phased Array Systems and Technology.Waltham：IEEE，2010：457-460.

［2］NITSCHKE S.Active phased array radar compared［J］. Naval Forces，2011，32（2）：18-24.

［3］ARUNRAJ N S，MAITI J.Risk-based maintenance policy selection using AHP and goal programming［J］.Safety Science，2010，48（2）：238-247.

［4］LEE W S，LIN Y C.Evaluating and ranking energy performance of office building using grey relational analysis［J］. Energy，2011，36（5）：2551-2556.

［5］GARCIA C M S，LAMATA M T.On rank reversal and TOPSIS method［J］.Mathematical and Computer Modelling， 2012，56：123-132.

［6］CHEN T Y，TSAO C Y.The interval-valued fuzzy TOPSIS method and experimental analysis［J］.Fuzzy Sets and Systems，2008，59（11）：1410-1428.

［7］ASHTIANI B，HAGHIGHIRAD F，MAKUI A，et al.Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets［J］.Applied Soft Computing Journal，2009，9（2）：457-461.

［8］GAU W L，BUEHRER D J.Vague sets［J］.IEEE Transactions on Systems，Man and Cybernetics，1993，23（2）：610-614.

［9］LIU F，ZHENG G L，WANG W P，et al.TOPSIS based on vague sets and its application in the scheme evaluation of mechanical design［C］//Proc.of 2010 Chinese Control and Decision Conference，Xuzhou：IEEE/Country of publication，2010：458-462.

［10］焦利明，于伟，李冬岩.用赋权公式法对战术防空C3I系统综合效能评估［J］.电光与控制，2006，13（4）：34-38.

［11］马亚龙，邵秋峰，孙明，等.评估理论和方法及其军事应用［M］.北京：国防工业出版社，2013.

［12］吴叶科，宋如顺，陈波.基于博弈论的综合赋权法的信息安全风险评估［J］.计算机工程与科学，2011，33（5）：9-13.

［13］苏观南，付修庆，刘天祥.改进的博弈论综合权重在大坝安全综合评价中的应用［J］.中国农村水利水电，2014（11）：82-85.

［14］杨宝臣，陈跃.基于变权和TOPSIS方法的灰色关联决策模型［J］.系统工程，2011，29（6）：106-112.

［15］杨红军，董礼.基于直觉模糊集多属性决策的灰色关联分析方法［J］.微电子学与计算机，2011，28（9）：155-157.

Research on Optimal Selection Method of Maintenance Concept for Phased Array Radar

WANG Yong-pan，YANG Jiang-ping，ZHANG Ke-xin，ZHANG Wei
（Air Force Early Warning Academy，Wuhan 430019，China）

Aiming at the selection problem of maintenance concept for phased array radar，this paper confirms the decision attributes firstly and then studies an optimal selection method based on TOPSIS theory.The proposed method introduces the Vague sets to dispose the fuzzy information in the process of selecting the maintenance concept，and it uses the game theory to calculate the weights of decision indexes.The grey relational grade with both ideal and negative-ideal maintenance concept is established to get the grey relational close-degree，and the ranks of all the alternative maintenance concept is also achieved at the end of this paper.Finally，applications and analysis of one example is conducted to verify the presented method.

maintenance concept，phased array radar，TOPSIS method，Vague sets，grey relational grades，game theory

TN95

A

1002-0640（2016）12-0054-05

2015-11-05

2015-12-27

军内科研项目（KJ2014023200B11145）；博士研究生专项课题基金资助项目（2014JY546）

王永攀（1987-），男，河北保定人，博士研究生。研究方向：预警装备管理与保障。