非线性随机参数模型的Legendre多项式逼近误差

严惠云,师义民

(西北工业大学 理学院,陕西 西安 710072)

非线性随机参数模型的Legendre多项式逼近误差

严惠云,师义民

(西北工业大学 理学院,陕西 西安 710072)

利用均方误差最小原则研究参数取值对Legendre多项式逼近误差的影响.分析数值解的均方误差,结果表明,模型参数的选取对近似逼近精度有显著影响,其中参数的标准差σ对近似逼近的精度影响最大,σ增大10倍时,近似逼近的均方误差可能会增加104倍.通过选取合适的参数Legendre多项式能有效逼近含有界随机参数的非线性经济周期模型.

Legendre多项式逼近法;有界随机参数;经济周期模型

0 引 言

在宏观经济问题研究中,影响经济运行的因素很多,且各因素联系紧密.而模型和实际问题间存在误差，这些误差在模型中主要以两种形式存在:一是作为模型的随机扰动项,二是隐含在参数中,此时参数就是随机参数.因此,研究随机参数对经济周期模型响应的影响有重要的理论意义和应用价值.

目前,研究含有界随机参数模型的方法主要有Monte Carlo方法[1-2],随机有限元法[3-4]和正交多项式逼近法[5-13].Monte Carlo方法简单但费时,随机有限元法只能解决随机参数是一个小量的情况,正交多项式逼近法则适用性更强.正交多项式逼近法应用较多的是第二类Chebyshev多项式．但并不是任何情况下都可以使用第二类Chebyshev多项式对模型进行近似逼近,应根据实际情况选择最合适的正交多项式.另外,在现有的研究成果中,很少见到对多项式近似逼近误差的讨论.没有考虑近似误差的多项式逼近有可能是无效的,因此,本文根据模型参数的实际意义,选取Legendre多项式作为正交多项式,以非线性经济周期模型为例,在均方误差最小的准则下讨论了参数取值对Legendre多项式近似逼近误差的影响.

1 含有界随机参数的非线性经济周期模型

根据Puu的投资函数[14]和Goodwin的消费函数[15],建立如下经济周期模型

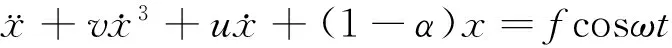
(1)

其中：x表示国民收入增长率,α(0≤α≤1)是边际消费率,表示资本市场的供需关系;v是边际投资率,满足v=1/(1-a),u=2α-1+1/(1-α);f与ω均为无量纲参数,分别表示周期噪声的强度和频率．由于不同时间的边际消费率不同,因此α是一个有界随机参数.

2 正交多项式基的选取(Legendre多项式)

由于ξ的分布没有先验信息,一般可以将ξ看作服从(-1,1)上均匀分布的随机变量,即ξ的概率密度函数为

(2)

基于上述的概率密度函数,本文选取Legendre多项式为正交多项式基. 这类多项式的一般表达式为

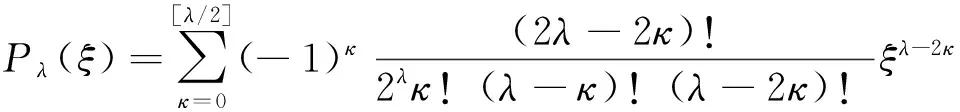
(3)

由此可以得到Legendre多项式的具体表达式，即

P0(ξ)=1,P1(ξ)=ξ,P2(ξ)=(3ξ2-1)/2,P3(ξ)=(5ξ3-3ξ)/2,…

(4)

由Legendre多项式三项式的递推公式,即

(l+1)Pl+1(ξ)=(2l+1)ξPl(ξ)-lPl-1(ξ),(l≥1),

可以得到

ξPl(ξ)=[(l+1)Pl+1(ξ)+lPl-1(ξ)]/(2l+1),(l≥1).

(5)

另外,Legendre多项式的正交性可表示为

(6)

3 Legendre多项式逼近

为方便后续推导,给式(1)两边同时乘以(1-α),得到

(7)

模型(7)的响应是关于时间t和ξ的函数

x=x(t,ξ).

(8)

由随机函数的正交分解法,模型(7)的响应可表示为

其中,Pl(ξ)是第l个Legendre多项式．在实际计算中,选取满足计算精度的有限项近似,即

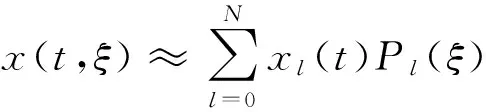
(9)

以N=4为例给出详细计算过程,N等于其他值的情况可以做类似推导.当N=4时,将式(9)代入式(7),得到

根据公式(5),有

式(10)两端同乘以p0(ξ),p1(ξ),p2(ξ),p3(ξ),p4(ξ), 关于ξ求期望得模型(7)的近似确定性系统(11),即

4 Legendre多项式逼近的均方误差

一个好的近似逼近应该有较小的近似误差.由于原模型和近似模型的解析解难以得到,因此本文用数值解分析参数取值对近似误差的影响.表1～5列出了N=2,3,4,5时近似确定性模型(11)与原模型(1)数值解的均方误差.

表 1 f=0时的均方误差表

由表1可以看出,当模型(1)没有周期性噪声扰动,即f=0时,不论Legendre近似逼近项数取多少,在其他参数不变的情况下,随着σ的增大,Legendre近似逼近的均方误差迅速增大.当σ增大10倍时,均方误差增加了104倍.由此看见σ的取值显著影响着Legendre近似逼近的精度,因此,在实际应用中应该选取较小的σ,以提高近似逼近精度.

表 2 σ=0.2, ω=0.43时的均方误差表

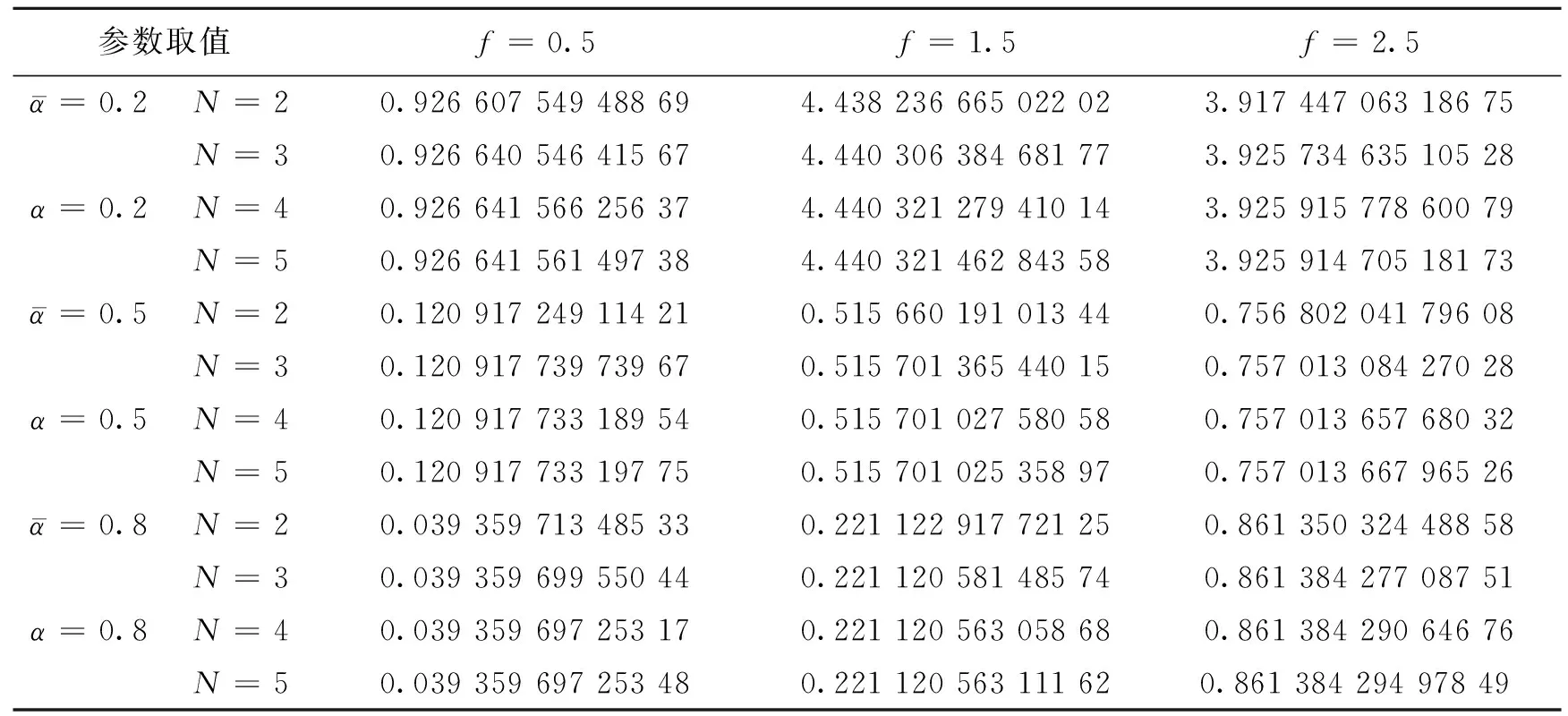
表 3 σ=0.1, ω=0.43时的均方误差表

表 4 σ=0.01, ω=0.43时的均方误差表

表 5 ω取值不同时的均方误差表

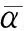
5 结束语

正交多项式逼近法使用简单而且应用广泛,但在实际应用中需要注意选择合适的正交多项式和近似项数.本文在均方误差最小的准则下讨论了参数取值对Legendre多项式近似逼近项数选取的影响.数值分析结果发现，模型参数取值对近似逼近误差有显著影响.随机参数的方差越大,均方误差越大,模型的周期扰动强度越大,均方误差越大.因此,在实际应用中,应根据参数的取值情况选取均方误差最小的近似逼近项数,且在满足精度要求的情况下,为了后续计算简便,尽可能选取项数较少的近似逼近.

[1] SHINO ZUKA M.Probability modeling of concrete structures[J].J Eng Mech Div ASCE,1972,98: 1433-1451.

[2] 杜永恩,王生楠,闫晓中.基于Neumann 展开的Monte-Carlo随机扩展有限元法[J].西北工业大学学报,2013,31(3):413-416.

DU Yong′en,WANG Shengnan,YAN Xiaozhong.Stochastically extended finite element method based on neumann expansion [J].Journal of Northwestern Polytechnical University,2013,31(3):413-416.

[3] 张义民,刘巧伶,闻邦椿.多自由度非线性随机参数振动系统响应分析的概率摄动有限元法[J].计算力学学报,2003,20(1):8-11.

ZHANG Yimin,LIU Qiaoling,WEN Bangchun.Probability perturbation finite element method for response analysis of multi-degree of freedom nonlinear vibration[J].Chinese Journal of Computational Mechanics,2003,20(1): 8-11.

[4] LIU W K,BEST ERFIED G H,BELYT S CHKO P.Variational approach to probabilistic finite elements[J].J Engng Mech,1988,114(12): 2115-2133.

[5] 侯璟,马少娟,沈琼.分数阶随机Duffing系统的Hopf分岔[J].动力学与控制,2014,12(4):310-314.

HOU Jing,MA Shaojuan,SHEN Qiong.Hopf bifurcation of fractional-order stochastic duffing system[J].Joural of Dynamics and Control,2014,12(4):310-314.

[6] 许勇,马少娟,张慧清.带有随机参数的随机Brusselator 系统的稳定性分析[J].中国科学:物理学，力学，天文学,2011,41(10): 1203-1209.

XU Yong,MA Shaojuan,ZHANG Huiqing.The stability analysis in stochastic brusselator system with random parameter[J].Cientia Sinica：Phys,Mech & Astron,2011,41(10): 1203-1209.

[7] 罗瑞芬,张建刚,杜文举.一个带有随机参数的新的二维混沌系统的随机Hopf分岔分析[J].温州大学学报:自然科学版,2016,37(1):26-35.

LUO Ruifen,ZHANG Jiangang,DU Wenju.Stochastic hopf bifurcation analysis of a novel two-dimensional chaotic system with random parameters[J].Journal of Wenzhou University:Natural Sciences,2016,37(1):26-35.

[8] SPANOS P D,GHANEM R G.Stochastic finite expansion for random media[J].J Engng Mech,1989,115(5): 1035-1053.

[9] JENSEN H,IWAN W D.Response of systems with uncertain parameters to stochastic excitation[J].J Engng Mech ASCE,1992,118(5): 1012-1025.

[10] LI J,LIAO S.Response analysis of stochastic parameter structure under non-stationary random excitation[J].Computational Mechanics,2001,27(1): 61-68.

[11] FANG T,LENG X L,SONG C Q.Chebyshev polynomial approximation for dynamic response problems of random structures[J].J Sound & Vibration,2003,266(1): 198-206.

[12] FANG T,LENG X L,MA X P,et al.K-PDF and gegenbauer polynomial approximation for dynamic response problems of random structure[J].Acta Mech Sinica,2004,20(3):292-298.

[13] 蒋水华,张曼,李典庆.基于Hermite 正交多项式逼近法的重力坝可靠度分析[J].武汉大学学报:工学版,2011,44(2):170-174.

JIANG Shuihua,ZHANG Man,LI Dianqing.Reliability analysis of gravity dam using hermite orthogonal polynomials approximation method[J].Engineering Journal of Wuhan University,2011,44(2):170-174.

[14] PUU T,SUSHKO I.A business cycle model with cubic non-linearity[J].Chaos,Solitons and Fractals,2004,19(3):597-612.

[15] 李伟,徐伟,赵俊峰.一个经济周期模型的稳定性及其近似计算[J].数学的实践与认识,2008,38(12):120-124.

LI Wei,XU Wei,ZHAO Junfeng.The stability and approximate solution of a business cycle model[J].Mathematics in Practice and the Theory,2008,38(12):120-124.

编辑、校对：师 琅

Study on approximation error of a nonlinear business cycle model with bounded random parameters

YANHuiyun,SHIYimin

(School of Science, Northwestern Polytechnical University, Xi′an 710072,China)

Based on the principle of minimum mean square error, the influence of parameters selection on the approximation error of Legendre polynomial approximation method is investigated.Analyzing the mean-square error of numerical solution,the results show that the selections of model parameters have great influence on approximate accuracy,and the standard deviation of parameter σ has the greatest influence on accuracy of approximation approach, whenσincreased 10 times, the mean square error of approximation approach is likely to increase 104times.By selecting suitable parameters, the Legendre polynomial approximation is an effective approach in equivalent approximation of a nonlinear business cycle model with bounded random parameters.

Legendre polynomial approximation; bounded random parameters; business cycle model

1006-8341(2016)04-0501-07

10.13338/j.issn.1006-8341.2016.04.015

2016-06-20

国家自然科学基金资助项目(71171164);陕西省教育厅科学研究计划项目(2014JK1276);陕西省统计研究中心基金资助项目(14DJ04)

严惠云(1977—)，女，陕西省宝鸡市人，西北工业大学博士研究生，研究方向为非线性动力学方法及其应用.E-mail:yanhuiyun@sina.com

严惠云,师义民.非线性随机参数模型的Legendre多项式逼近误差[J].纺织高校基础科学学报,2016,29(4)：501-506.

YAN Huiyun,SHI Yimin.Study on approximation error of a nonlinear business cycle model with bounded random parameters[J].Basic Sciences Journal of Textile Universities,2016,29(4):501-506.

O 242.2

A