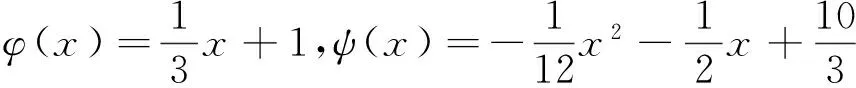含不连续系数的时滞微分方程奇摄动边值问题
阳广志,谢 峰
(东华大学 应用数学系,上海 201620)
含不连续系数的时滞微分方程奇摄动边值问题
阳广志,谢 峰
(东华大学 应用数学系,上海 201620)
研究一类含不连续系数的二阶时滞微分方程的奇摄动问题.原问题可看作左问题与右问题的藕合,利用边界层函数法分别构造左右问题的渐近解从而得到其解的零阶近似, 再利用缝接法得到整个区间上的解,最后运用上下解引理证明解的存在性.
时滞;不连续系数;奇摄动;上下解;缝接法
0 引 言
关于时滞微分方程的边值问题已受到广泛而深入的讨论[1-5], 但主要都集中在连续情形下的奇异摄动时滞问题[6-10], 对一些含不连续系数或不连续源项的奇摄动时滞问题研究相对较少. 近几十年来, 在物理、 化学、 生物以及环境学等许多领域的数学模型都可归结为带有不连续系数或不连续源项的奇摄动时滞问题,并备受研究者重视,但研究主要集中在数值方法方面[11-12].2015年,Subburayan[12]研究了一类具有不连续对流系数的二阶线性奇摄动时滞问题,并结合文献[13]给出了分段线性插值Shishkin网格的数值方法.
本文主要研究下述含不连续源项的时滞微分方程的奇摄动边值问题
εx″(t)+f(t,x(t))x′(t)=g(t,x(t),x(t-τ)),t∈(0,τ)∪(τ,1),
(1)
x(t)=φ(t),t∈[-τ,0];x(1)=A.
(2)
其中
1 上下解引理
考虑如下非线性边值问题
x″(t)=f(t,x(t),x(t-τ),x′(t)),t∈(0,τ)∪(τ,1),
(3)
x(t)=φ(t),t∈[-τ,0];x(1)=A.
(4)
其中
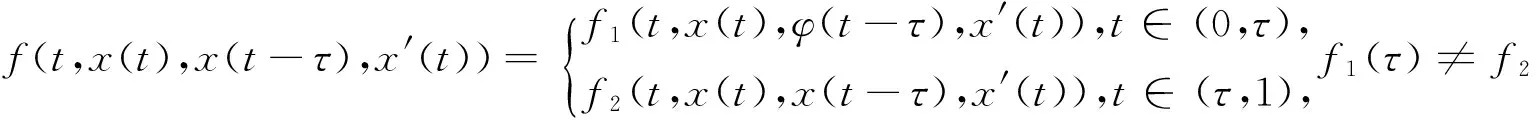
引理1 假设(H1)f(t,x,y,z)于[0,τ)∪(τ,1]×R3上连续,且对∀r>0,存在[0,+∞)上的正值连续函数h(s)满足
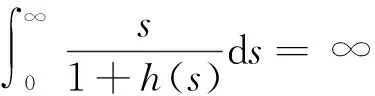
且当t∈[0,1],|x|≤r,|y|≤r,|z|<∞时有
|f(t,x,y,z)|≤h(|z|).
(H2)f(t,x,y,z)关于y单调不增.
(H3)存在函数α(t),β(t)∈C[-τ,1]∩C2[0,τ)∪(τ,1],满足
α(t)≤β(t),t∈[-τ,1];α′(τ-)≤α′(τ+),β′(τ-)≥β′(τ+),
α″(t)≥f(t,α(t),x(t-τ),α′(t)),t∈(0,τ)∪(τ,1),
β″(t)≤f(t,β(t),x(t-τ),β′(t)),t∈(0,τ)∪(τ,1)
则∀φ(t)∈C[-τ,0],当α(t)≤φ(t)≤β(t),t∈[-τ,0],α(1)≤A≤β(1)时,边值问题(3)~(4)有解x(t)∈C1[-τ,1]∩C2([0,τ)∪(τ,1]), 满足
α(t)≤x(t)≤β(t),t∈[0,1].
(5)
其中
yβ(τ)=β(t-τ),yα(τ)=α(t-τ).
又令

有解.
下面先证明解x(t)满足不等式(5).以下只证明x(t)≤β(t)(因为α(t)≤x(t)可类似处理). 用反证法, 设存在一点t0∈[0,1]使得x(t0)>β(t0), 则由于x(0)=φ(0)≤β(0), x(1)=A≤β(1), 函数x(t)-β(t)必在(0,1)内的某点ξ处取正的极大值, 从而x(ξ)>β(ξ), x′(ξ)=β′(ξ), x″(ξ)≤β″(ξ). 但依据(H2)和(H3), 当ξ∈(0,τ)时,有
这与x″(ξ)-β″(ξ)≤0矛盾.
同理当ξ∈(τ,1)时也推出矛盾.
当ξ=τ时,x(t)-β(t)在τ处取得正的极大值,从而有
类似可得x″(τ+)-β″(τ+)>0,这与x″(τ±)≤β″(τ±)矛盾.
再证|x′(t)|≤M(0≤t≤1),若此不等式不成立,即存在一点t1∈[0,1],使得|x′(t1)|>M.由中值定理,必存在ξ∈(0,1)使得x′(ξ)=x(1)-x(0),故|x′(ξ)|≤2r.又从x′(t)的连续性知,存在τ1,τ2∈[0,1],使得
|x′(τ1)|=2r,|x′(τ2)|=M,
且当τ1 这与M的取法矛盾, 故|x′(t)|≤M(0≤t≤1). 即有|x(t)|≤M(0≤t≤1), 从而x(t)就是原问题的解. 由于原问题在t=τ处间断, 所以会产生内部层, 因此可以把问题(1)~(2)看成是以下两个问题的光滑连接. 左问题PL: εx″(t)+f1(t,x(t))x′(t)=g1(t,x(t),φ(t-τ)),t∈(0,τ), (6) x(0)=φ(0),xL(τ)=γ(ε). (7) 右问题PR: εx″(t)+f2(t,x(t))x′(t)=g2(t,x(t),x(t-τ)),t∈(τ,1), (8) xR(τ)=γ(ε),x(1)=A. (9) 其中γ(ε)是与ε有关的待定参数. 现作如下假设: (ⅰ) 函数f1(t,x), g1(t,x,y)在[0,τ]×R3上连续, f2(t,x), g2(t,x,y)在[τ,1]×R3上连续, 且gi(i=1,2)关于y单调不增; (ⅱ) 初值问题f1(t,x(t))x′(t)=g1(t,x(t),φ(t-τ)), x(0)=φ(0)有解φ1(t)∈[0,τ]; (ⅲ) 初值问题f2(t,x(t))x′(t)=g2(t,x(t),x(t-τ)), x(1)=A有解φ2(t)∈C2[0,1]; (ⅳ) f1(t,x)≤-σ1<0,(t,x)∈[0,τ]×R; f2(t,x)≥σ2>0,(t,x)∈[τ,1]×R. 首先考虑左问题的渐近解构造, 假设左问题PL的形式渐近解表达式为 (10) 其中 (11) VL(η)=V0L(η)+εV1L(η)+ε2V2L(η)+…, (12) γ(ε)=γ0+εγ1+ε2γ2+…. (13) 将式(10)代入式(6)并分离变量,再根据ε同次幂系数相等, 可得到一系列递推等式. 为了简单起见, 以下只考虑零阶近似. (14) 同时可得边界层项V0L(η)满足如下边值问题 (15) (16) 由文献[16]中引理1以及条件(ⅰ),(ⅱ),(ⅳ)可知, 边值问题(15)~(16)存在解V0L(η)且满足指数估计, 即存在正常数K1, 使得 |V0L(η)|≤K1exp(σ1η). 因此, 可得左问题的零阶近似渐近解形式为 xL(t)=φ1(t)+V0L(η),t∈[0,τ]. (17) 同左问题, 可得右问题的零阶近似渐近解形式为 (18) (19) 边界层项V0R(η)满足边值问题 (20) (21) 由文献[16]中引理2以及条件(ⅰ),(ⅲ),(ⅳ)可知, 边值问题(20)~(21)存在解V0R(η)且满足指数估计, 即存在正常数K2, 使得 |V0R(η)|≤K2exp(-σ2η). 为了使左问题的解与右问题的解在t=τ处光滑连接,须有 (22) (17),(18)代入代(22)得 (23) (24) 同理, 由式(20)和(21)可推出 (25) 将式(24), (25)代入式(23)得 (26) 易知式(26)的右边是负值, 则γ0可以由式(26)决定.同理γi(i≥1)也可由此递推得到. 因此, 可得问题(1)~(2)的形式渐近解. 定理1 假设条件(ⅰ)~(ⅳ)成立, 则对于充分小的ε>0, 边值问题(1)~(3)有一个C1光滑解x(t)满足 其中 现证明定理1,首先构造合适的上下解.记 根据近似解的构造过程和假设(ⅰ)知, 存在正常数M使得 |εx″(t)+f(t,x(t)x′(t)-g(t,x(t),x(t-τ)))|≤Mε2,t∈[0,1], (27) (29) 令 其中 容易验证, λ(t)是一个正值连续函数且具有如下性质 (30) (31) 再依据式(29)~(30), 有 α(t),β(t)∈C([0,1]),α(t)<β(t),t∈[0,1], α′(τ-)≤α′(τ+),β′(τ-)≥β′(τ+),α(0)<φ(0)<β(0),α(1) 下面验证不等式εα″(t)+f(t,α(t))α′(t)≥g(t,α(t),α(t-τ)).仅考虑区间(τ,1)上,在(0,τ)上可类似证明.根据式(27), (28)以及(30), (31)可得 其中0<θ1,θ2,θ3<1. 类似可得对充分小的ε>0,不等式 εβ″(t)+f(t,β(t))β′(t)≤g(t,β(t),β(t-τ)),t∈(0,τ)∪(τ,1) 成立. 以上证明了α(t),β(t)分别是问题(1)~(3)的下解和上解. 由上下解引理可知, 问题(1)~(2)存在解 x(t)∈C1[0,1]∩C2((0,τ)∪(τ,1)), 且∀t∈[0,1]有α(t)≤x(t)≤β(t),证毕. 考虑如下问题 (32) 将问题(32)看成是以下两个问题的光滑连接. 左问题: (33) 右问题: (34) 其中γ(ε)是与ε有关的待定参数.可令 γ(ε)=γ0+εγ1+ε2γ2+…, 根据前面的构造方法, 可得左右问题的退化解分别为φ(x)∈[0,1],ψ(x)∈[0,2], 且 再由式(15)~(16)以及(20)~(21)可求出左右问题边界层函数的零阶近似V0L(η),V0R(η)分别为 从而问题(32)的零阶近似解可表示为 [1] MO Jiaqi,WEN Zhaohui.Singularly perturbed reaction diffusion equations with time delay[J].Applied Mathematics and Mechanics,2010,31(6):769-774. [2] 郑春华,郑艳艳.一类二阶时滞微分方程三点边值迭代解的存在性[J].纺织高校基础科学学报,2015,28(2):218-223. ZHENG Chunhua,ZHENG Yanyan.Existence of monotone interation solutions for a kind of second-order delay differential equations with three-point boundary value problem[J].Basic Sciences Journal of Textile Universities,2015,28(2):218-223. [3] 郑春华.一类时滞微分方程非局部共振问题解的存在性[J].纺织高校基础科学学报,2012,25(3):279-283. ZHENG Chunhua.The existence of solutions for a nonlocal boundary value problem at resonance of differential equation with delay[J].Basic Sciences Journal of Textile Universities,2012,25(3):279-283. [4] 汪娜,倪明康.经典物理中的扰动时滞模型解[J].物理学报,2011,60(5):1-7. WANG Na,NI Mingkang.Disturbance delay model of classical physics[J].Journal of Physics,2011,60(5):1-7. [5] 莫嘉琪.一类非线性时滞反应扩散系统奇摄动问题[J].系统科学与数学,2000,20(4):412-416. MO Jiaqi.A class of nonlinear singularly perturbed problems for reaction diffusion equation with time delays[J].System Science and Mathematics,2000,20(4):412-416. [6] 张祥.时滞反应扩散方程初边值问题奇摄动[J].应用数学和力学,1994,15(3):253-258. ZHANG Xiang.Singular perturbation of initial-boundary value problems of reaction diffusion equation with delay[J].Applied Mathematics and Mechanics,1994,15(3):253-258. [7] 倪明康.一类含时滞奇摄动抛物型方程的初边值问题[J].华东师范大学学报,1992(3):1-7. NI Mingkang.The initial and boundary value problems of singularly perturbed partial differential equations with time lag of parabolic type[J].Journal of East China Normal University,1992(3):1-7. [8] CHEN Huaijun.Perturbed problem for a class of reaction diffusion with time delay[J].Journal of Anhui Normal University,2011,34(6):511-515. [9] 周津,程燕.二阶非线性时滞微分方程的奇异摄动[J].合肥工业大学学报,2013,36(4):483-485. ZHOU Jin,CHENG Yan.Singular perturbation of second order nonlinear delay differential equation[J].Journal of Hefei University of Technology,2013,36(4):483-485. [10] 谢英超,程燕.一类非线性时滞微分方程的奇摄动研究[J].安徽师范大学学报,2015,38(2):129-133. XIE Yingchao,CHENG Yan.Singularly perturbed study on a class of nonlinear delay differential equation[J].Journal of Anhui Normal University,2015,38(2):129-133. [11] SUBBURAYAN V,RAMANUJAM N.An initial value technique for singularly perturbed convection diffusion problems with a negative shift[J].J Optim Theory Appl,2013,158(1):234-250. [12] SUBBURAYAN V.A parameter uniform numerical method for singularly perturbed delay problems with discontinuous convection coefficient[J].Arab Journal Mathematical Sciences,2015,22(2):191-206. [13] FARRELL P A,HEGARTY A F,MILLER J J H,et al.Globle maximum norm parameter uniform numerical method for a singularly perturbed convection-diffusion problems with discontinuous convection coefficient[J].Mathematics and Computer Modelling,2004,40(11/12):1375-1392. [14] 刘江瑞,王国灿.时滞非线性系统的奇异摄动[J].大连铁道学院学报,1995,16(2):26-31. LIU Jiangrui,WANG Guocan.Singular perturbation of nonlinear system with delay[J].Journal of Dalian Railway Institute,1995,16(2):26-31. [15] BERNFELD S R,LASHMIKAN Than V.An introduction to nonlinear boundary value problems[M].New York:Academic Press,1974. [16] XIE Feng,HU Pan.Singularly perturbed quasilinear boundary value problems with discontinuous coefficients[J].Communication on Applied Mathematics and Computation,2013,27(4):522-532. 编辑、校对:师 琅 Singularly perturbed boundary value problems of differential equations with delay and discontinuous coefficients YANGGuangzhi,XIEFeng (Department of Applied Mathematics, Donghua University, Shanghai 201620, China) A class of singularly perturbed problems of second-order delay differential equations with discontinuous coefficients are studied. The original problem can be viewed as the coupling of the left and right problem. Asymptotic solutions of the left and right problem are constructed by using the method of boundary function respectively, so that the solution of zero order approximation is obtained. To make the solution set up on the whole interval, the sewing method is used. At last, the existence of solution are proved by the theorem of lower and upper solutions. delay; discontinuity coefficients; singular perturbation; lower and upper solution;sewing method 1006-8341(2016)04-0435-08 10.13338/j.issn.1006-8341.2016.04.004 2016-05-28 上海市自然科学基金资助项目(15ZR1400800) 谢峰(1976—),男,安徽省宿州市人,东华大学教授,研究方向为常微分方程与动力系统,奇异摄动理论及其应用.E-mail:fxie@dhu.edu.cn 阳广志,谢峰.含不连续系数的时滞微分方程奇摄动边值问题[J].纺织高校基础科学学报,2016,29(4):435-442. YANG Guangzhi XIE Feng.Singularly perturbed boundary value problems of differential equations with delay and discontinuous coefficients[J].Basic Sciences Journal of Textile Universities,2016,29(4):435-442. O 175.14 A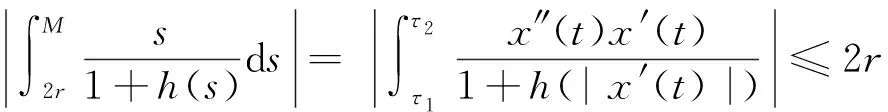
2 渐近解的构造
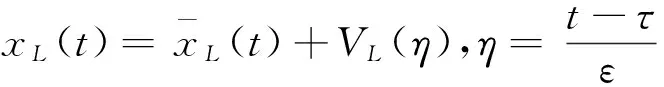

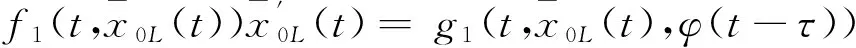



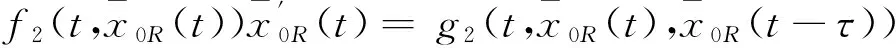
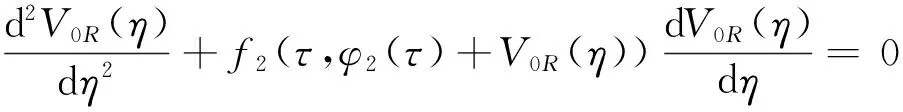
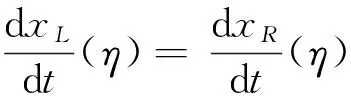
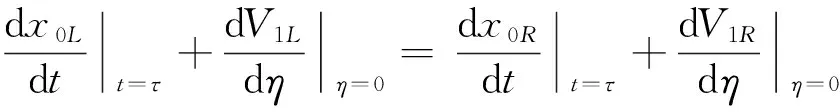



3 定理的证明
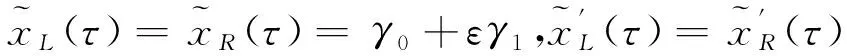


4 应用举例